斜支柱小水线面双体船水动力性能的数值研究
2019-12-31毛立夫李英辉
毛立夫,李英辉,易 宏
(上海交通大学 海洋智能装备与系统教育部重点实验室; 海洋工程国家重点实验室;高新船舶与深海开发装备协同创新中心, 上海 200240)
小水线面双体(SWATH)船是一种通过流线型支柱连接排水部分及水上部分的船型[1],其排水体积主要集中于除支柱外的水下部分(鱼雷体),因其深埋于水中,故受到的波浪干扰力、在大风浪中的失速、运动响应幅值、运动加速度幅值均较小.此外,与排水量相当的常规单体船及双体船相比,该船型的水线面较小,纵摇及横摇固有运动周期较大,在斜浪中不易发生斜摇,具备优良的耐波性能.SWATH船具有适于远洋航行、风浪中出航率高、波浪失速少、晕船率低、工作效率高等优点[2],在海上交通、海洋调查、水声监测等领域受到了广泛的应用.目前,在新兴的水面无人艇领域的应用也备受关注[3].除了采用常规直立支柱的SWATH船外,具有良好隐身特点的斜支柱小水线面双体(I-SWATH)船也逐渐得到了开发与应用[4].
较小的水线面积能使SWATH船获得较大的垂荡、纵摇及横摇固有运动周期,从而避开与中等以下海浪的主要波频成分发生谐振,降低波浪中的运动响应.但其垂荡及纵摇回复力(矩)相对较小,在对应的谐振频率处其响应峰值较高.当有义波高较低时, SWATH船具有较小的晕船率(MSI);但当有义波高大于3.0m (高于四级海况)后,MSI将会快速增大,导致船员和旅客的舒适感降低.这是由于随着有义波高的增加及波浪周期的延长,SWATH船的遭遇频率逐渐靠近最大响应频率(谐振频率),致使运动响应越来越剧烈[5].为了改善SWATH船耐波性能的不足,研究人员研发出一种具有倾斜支柱的SWATH船.
有关SWATH船的水动力性能,国内外的学者做了大量研究.如毛筱菲[6]、刘志华等[7]均基于二维切片理论,采用半经验方法考虑黏性及稳定鳍的影响,对SWATH船的耐波性进行了大量的数值研究.林鹏等[8]基于重叠网格技术研究纵向航态对SWATH船的阻力影响.考虑模型试验的尺度效应,Dubrovsky 等[9]分析了SWATH船的形状阻力并总结了影响剩余阻力的因素.Lei 等[10]基于雷诺平均Navier-Stokes (RANS)方程和流体体积(VOF)模型求解黏性兴波流场,并开展了SWATH船在迎浪规则波中纵向运动及波浪载荷的非线性研究.然而,除了Brizzolara等[1,3]对一艘内倾式支柱SWATH船水下潜体的阻力进行优化外,上述学者的研究工作多集中于常规直支柱的SWATH船上.
倾斜支柱的最初设想源于Techet[11]关于将振动翼作为新型高效船用推进器的研究设想.鉴于振动翼自身类似鱼鳍的二维摆动能够产生推力,当具有倾斜支柱的SWATH船在波浪中进行垂荡及纵摇运动时,斜支柱的运动形式类似于振动翼的二维摆动,因此可能能够利用由波浪产生的推力[12-13].为此在前期工作[4,14-16]中,运用 STF(Salvesen,Tuck,Faltinsen)切片理论考虑片体之间的干扰,对I-SWATH船的耐波性进行频域分析,并基于RANS方程对其在低速段(弗劳德数Fr<0.35)的耐波性做了初步研究,发现其波浪增阻较小,运动响应呈现出一定的非线性,且运动周期大于波浪遭遇周期.
但由于STF切片理论忽略了黏性阻尼,运动响应的计算结果往往偏高.虽然能够获得垂荡、纵摇及波浪增阻的大致变化规律,但在每个遭遇频率下的计算精确度较差(尤其在高速段Fr>0.4),并不能反映出局部细节的特性.此外,虽然I-SWATH船的片体和支柱可以看作是细长体,但由于倾斜支柱与自由面是斜交的,形成的不对称流场引起的泄涡在很大程度上影响了阻尼和阻力.Latorre等[17]通过模型试验及数值计算,发现黏性对运动响应预报有较大的影响.因此,为了进一步研究该船型在波浪中的运动响应,本文利用考虑黏性阻尼的三维面元法进行频域分析,改善计算结果的精确度;然后,基于求解 RANS方程的黏流理论,对该船型在规则波中的水动力性能进行数值计算;数值模拟中运用重叠网格方法[8],更好地模拟了高航速下船体的大幅度运动,拓展了前期的研究工作,获得了更加合理而精准的结论.
1 模型介绍
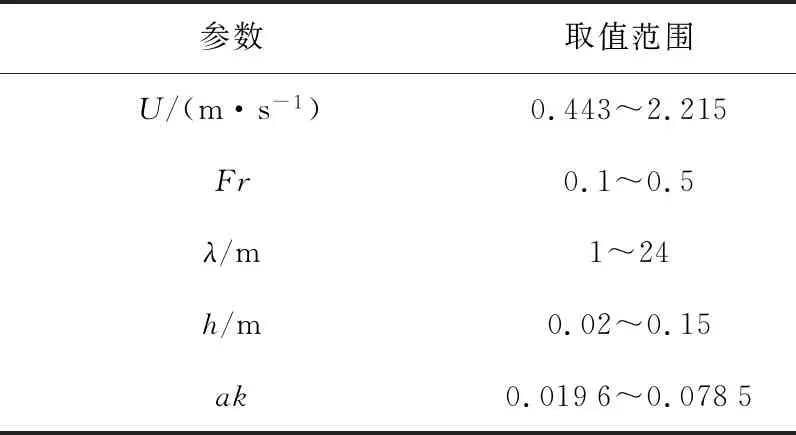
基于前期关于I-SWATH船的研究[4,14-16],所研究的船体轮廓图如图1所示,其主要参数取值如表1所示.其中,数值计算模型与实船的缩尺比为 1∶10.

图1 I-SWATH船的轮廓图Fig.1 The porifiles of I-SWATH ship
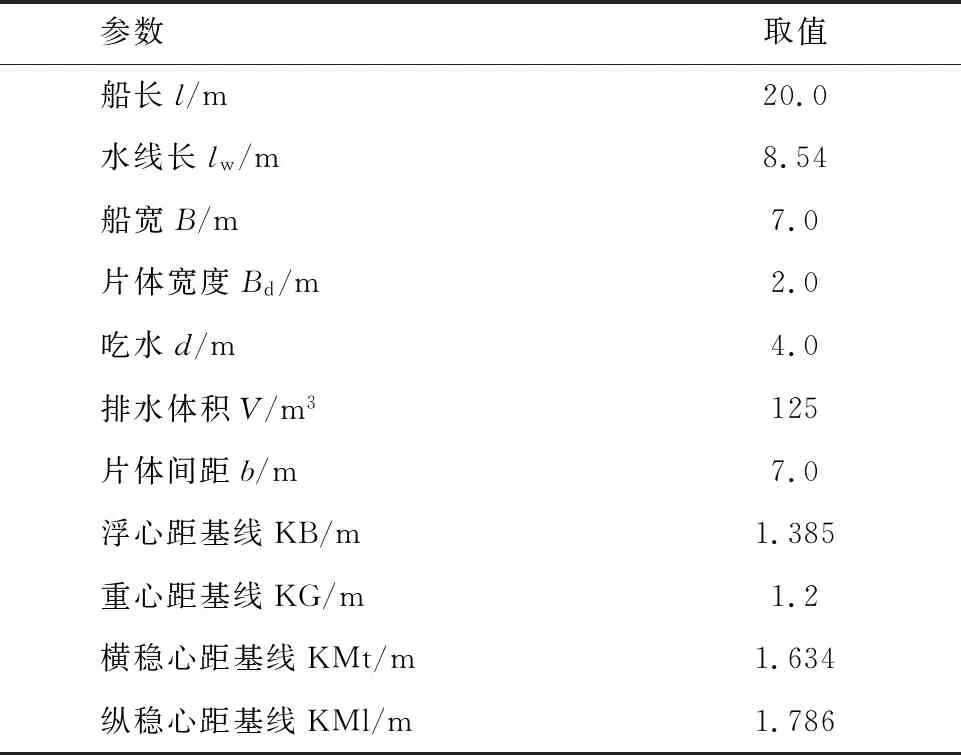
表1 I-SWATH船的主尺度参数Tab.1 Principal dimensions of I-SWATH ship
这种非常规SWATH船的设计初衷是在恶劣海况下,探究利用倾斜支柱作为水面无人艇的适航性及生存能力.根据仿生流体动力学[18]及鱼的形状,将倾斜支柱设置在船尾附近,以期倾斜支柱可通过水下鱼雷体引起的流动产生推进力.本文重点探究了I-SWATH船在迎浪规则波中的水动力性能,为了简化问题,在所有数值模拟中均不考虑上层结构.
2 基于三维面元法的耐波性频域分析
在单体船中,三维势流理论已经被广泛地应用于计算船体的耐波性,且其计算精度较好.但对于双体船而言,除了直接应用三维势流理论,还需要考虑黏性阻尼对于船体垂荡及纵摇的影响.大量的理论及试验研究表明:在不考虑黏性影响的情况下,直接使用三维势流理论计算双体船的运动响应(垂荡及纵摇)将会导致计算结果明显偏大.

图2 船体的坐标系及其运动Fig.2 Depiction of ship coordinate systems and its motions
2.1 坐标系
为了描述船体的6自由度运动,建立两套右手直角坐标系,如图2所示:大地固定坐标系O-XYZ和固定在船上的随体坐标系o-xyz.前者固定在流场中,不随流体或船体运动;OXY平面与静水面重合,OZ轴竖直向上.后者随船体一起运动,其坐标原点在船体的重心处;ox轴位于纵中平面内并指向船首,oy轴指向左舷;当船舶处于平衡位置时,oxy平面与静水面平行,oz轴竖直向上.
2.2 基本方程及其边界条件
设船以恒定速度U航行,暂不考虑舵、鳍、桨的影响;基于三维势流理论,假定流体为无黏、均匀、不可压缩的无旋流体;船体视为刚体,在平衡位置做6自由度的摇荡运动;入射波为微幅波,则船体各模态的摇荡运动可视为遭遇频率为ωe的简谐振动.用标量函数速度势Φ(x,y,z,t)描述速度分布.该速度势包括船体恒速航行时产生的定常速度势Φs(x,y,z)、入射波速度势Φ0(x,y,z,t)、入射波遭遇船体时产生的绕射势Φ7(x,y,z,t)、船体摇荡运动时产生的辐射势ΦD(x,y,z,t).根据线性势流理论的叠加原理,总速度势可以表示为
Φ(x,y,z,t)=Φs(x,y,z)+Φ0(x,y,z,t)+
Φ7(x,y,z,t)+ΦD(x,y,z,t)
(1)
将非定常速度势部分的时间因子分离出来,可以写成以下形式
Φ0(x,y,z,t)+Φ7(x,y,z,t)+ΦD(x,y,z,t)=
(2)
式中:i=1,2,…,6;φ0为入射波的空间速度势;φj为6自由度运动各模态所对应的规范化速度势,j= 1, 2,…,7;Xj为6自由度运动各模态所对应的运动幅值,j= 1, 2,…,7;当j=1,2,…,6时,分别为船体的纵荡、横荡、垂荡、横摇、纵摇和艏摇运动,当j=7时,为绕射势的空间速度势.
规则入射波的速度势可以为
(3)
式中:a为波幅;λ为入射波长;β为入射波浪向角;k=2π/λ为波数;ω为波浪频率;H为水深;g为重力加速度.k与ω满足色散关系ω2=gktanhkH.
绕射势和辐射势应满足以下边界条件:
流域内
Δφj=0,j=1,2,…,7
自由液面上
j=1,2,…,7
湿表面上
当z=-H时
辐射条件
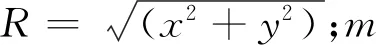
(4)
2.3 船体运动方程
通过上述速度势可求解波浪力,代入船体在波浪中的运动方程即可求解船体的运动
(5)
i=1,2,…,6;j=1,2,…,6
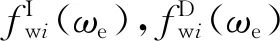
2.4 黏性阻尼
对于常规单体船竖直面内的运动,由于兴波阻尼占主要部分,黏性阻尼常被忽略不计.然而,SWATH船的片体被埋在水下,产生的水面兴波较小,兴波阻尼所占比例也相对较小.此外,由于其水下片体的横向尺度要大于支柱,且倾斜支柱与自由面是斜交的,形成的不对称流场引起的泄涡在很大程度上会同时影响阻尼和阻力,所以黏性阻尼不能忽略.否则,计算得到的运动幅值在响应频率附近将呈现出典型的欠阻尼线性导致计算结果的正确率有所下降[19].
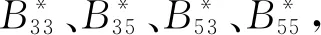
计算上述附加水动力系数以及干扰力时,所需的交叉流阻力项需要预先知道船体的运动幅值,所以可以先不考虑交叉流阻尼,利用式(6)求出运动幅值;然后,利用该幅值计算交叉流阻力项获得附加水动力系数和附加干扰力并代入式(6),进而获得考虑黏性阻尼的运动幅值;按此方法反复迭代直到获得一个合理的收敛结果,通常迭代3~5次即可[20].
高校的教育目的是为了社会需要培养优秀人才,为了企业需求培养定向型专业人才,随着社会形式的不断发展,社会对人才水平的需要也在不断提高。经济管理专业与社会发展、地方经济有着不可忽视的关系。经济管理高校以培养经济管理操作能力与管理理论兼具的经济管理专业型人才为目标,在知识理论与实际相结合的前提下,大大提高经济管理人才的培养效果,同时也有利于形成学校和企业双赢的局面。经济管理教学要与当下社会经济环境相融合,有针对的为社会经济需要培养相应经济管理人才。传统的经济管理教学已不能满足现今社会发展速度,校企合作模式是通过企业对人才实际需要的前提下,联合高校共同建立培养企业所需人才的机制。
2.5 计算结果
2.5.1算法验证 利用上述方法考虑黏性阻尼的影响,通过自编程序计算得到的迎浪时代尔夫特双体船(Delft-Cata)与试验数据(TS1)[21]以及切片法(STF)的垂荡及纵摇运动响应幅值算子(RAO)计算结果的对比情况如图3所示.由图3可知,考虑黏性阻尼后,STF与TS1的计算结果吻合程度更高,在一定程度上能够提供更多的局部细节特征,可用于进一步探究I-SWATH船的耐波性能.
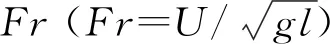
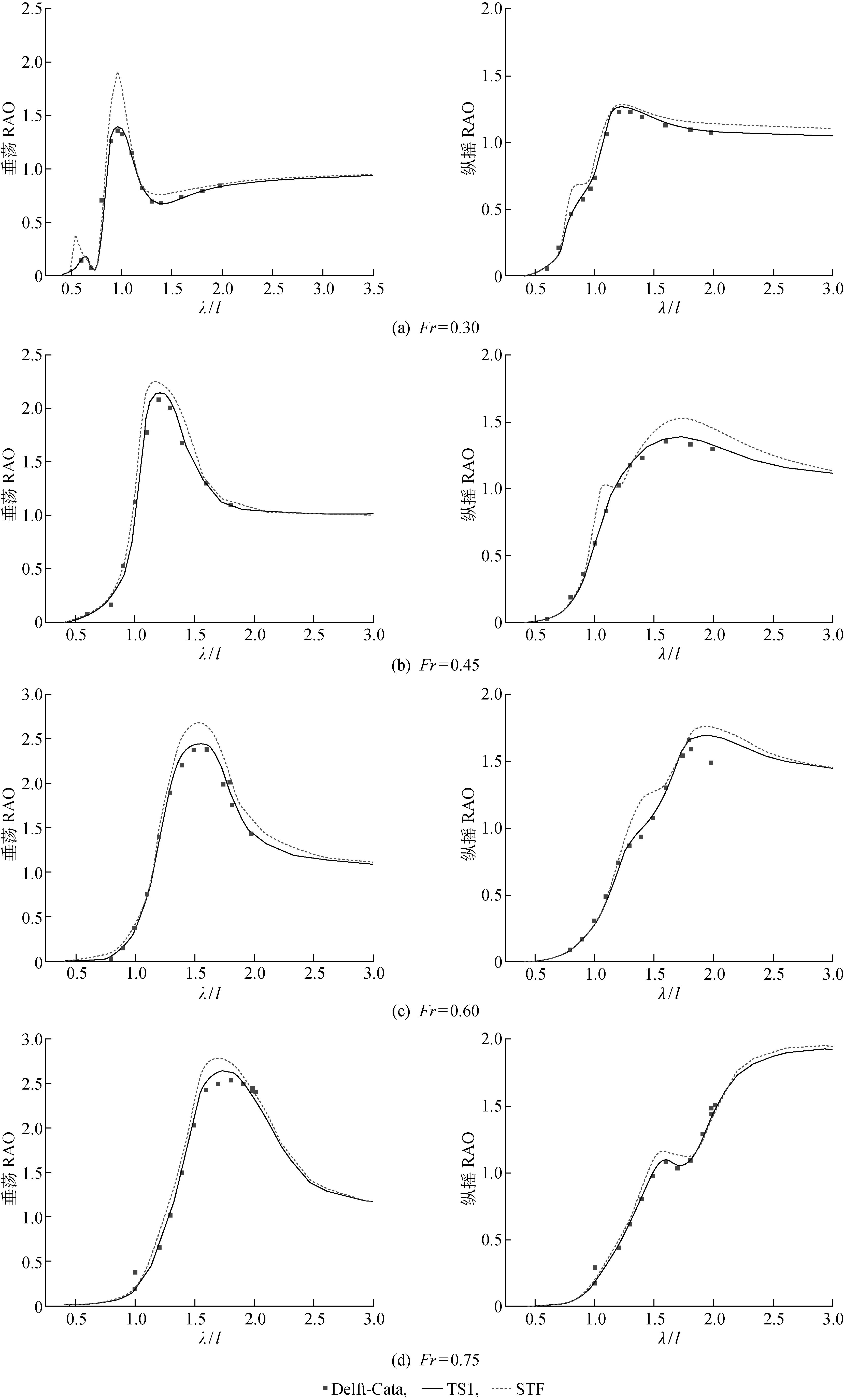
图3 TS1和STF的计算结果与Delft-Cata的试验结果对比图Fig.3 The experimental results of TS1 and STF calculation results compared to Delft-Cata test results
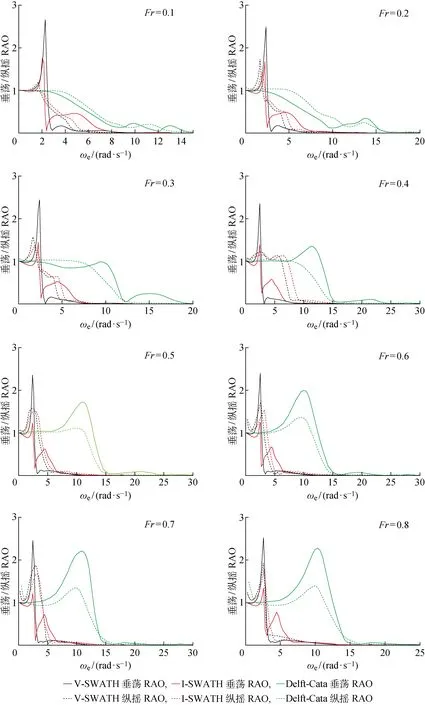
图4 I-SWATH与V-SWATH和Delft-Cata的垂荡和纵摇RAO对比Fig.4 Comparison of the heave and pitch RAO calculated for I-SWATH, V-SWATH and Delft-Cata
3 静水与规则波中的水动力性能
3.1 数值计算原理
由于非常规SWATH船的倾斜支柱与自由面斜交,所形成不对称流场引起的泄涡在很大程度上影响了阻尼和阻力.为了充分考虑黏性,基于RANS方程采用同质多相流Euler方法捕捉自由液面.假设在每个空间有单一的时间平均速度场ui(i=1,2,3, 分别代表x、y、z3个方向),则不稳定的黏性流体控制方程为
(6)
(7)
式中:p为压力;ρm为混合密度;ρα和rα分别为介质α的密度和体积系数,其中α=1代表介质为水,α=2代表介质为空气;μm为混合黏性系数.则有
增量方程采用的湍流模型为SSTk-ω方程,壁面函数为All Y+型,并加入6自由度刚体运动计算模块以及波浪生成模块.采用规则波浪,其波浪方程定义如下:
z=acos(kx-ωe+δ)
(10)
式中:δ为初始相位.
波数和波浪频率满足色散关系.根据线性波浪理论,规则波的速度势为
(11)
进而得到水质点在x、z方向的速度分量分别为
(12)
(13)
波浪生成模块与RANS方程的结合已经在前期工作[4]中得到了验证,可用于本研究.
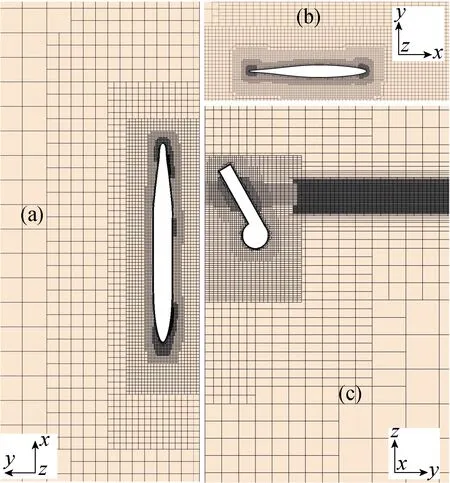
3.2 网格划分及边界条件
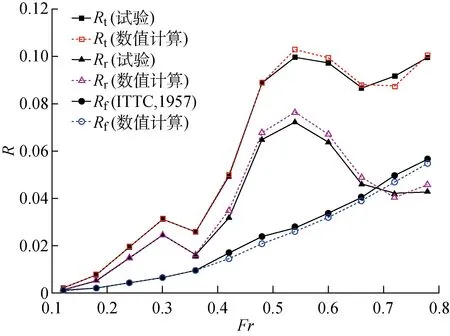
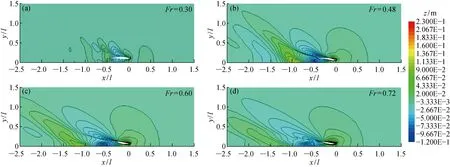
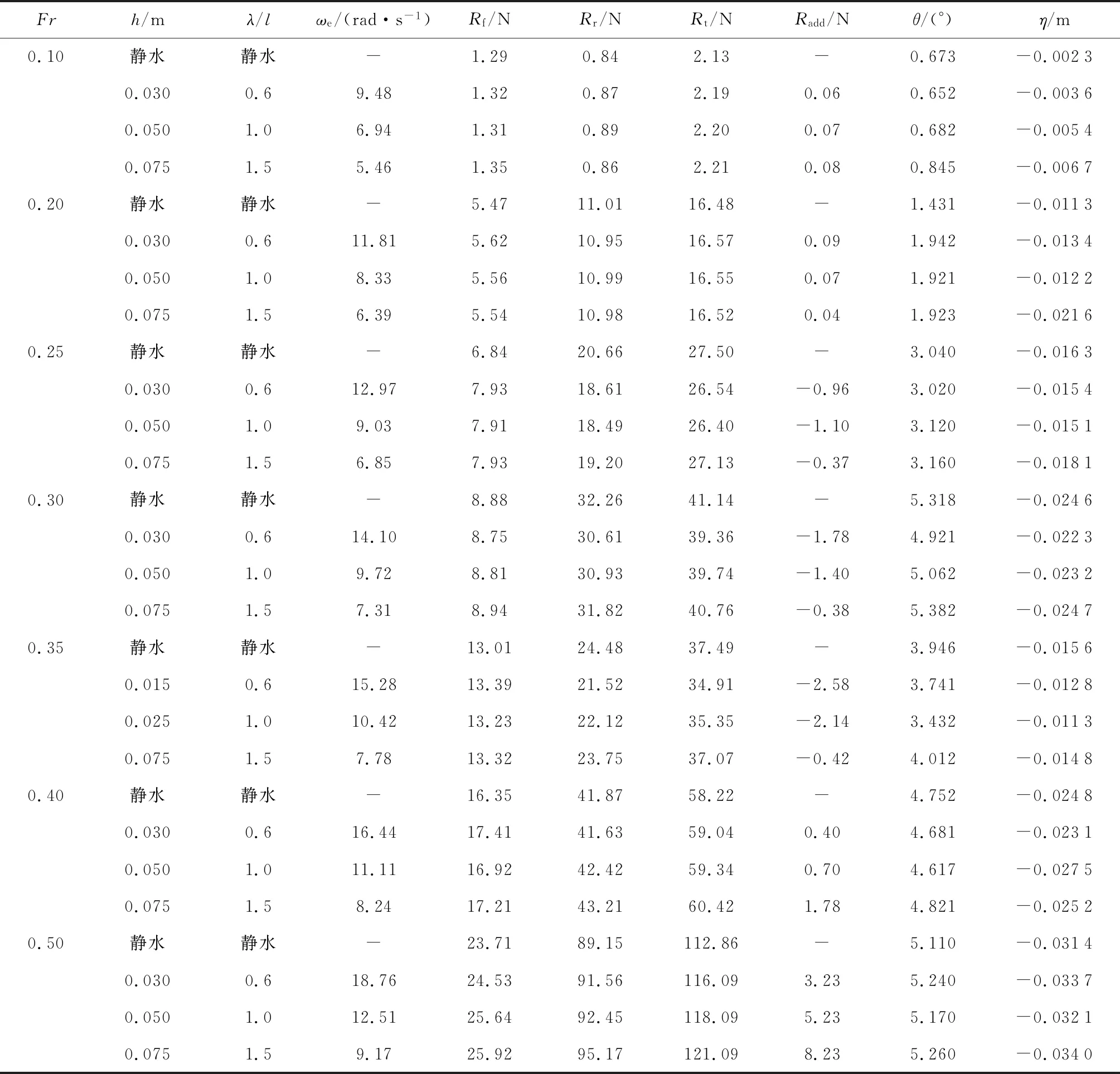
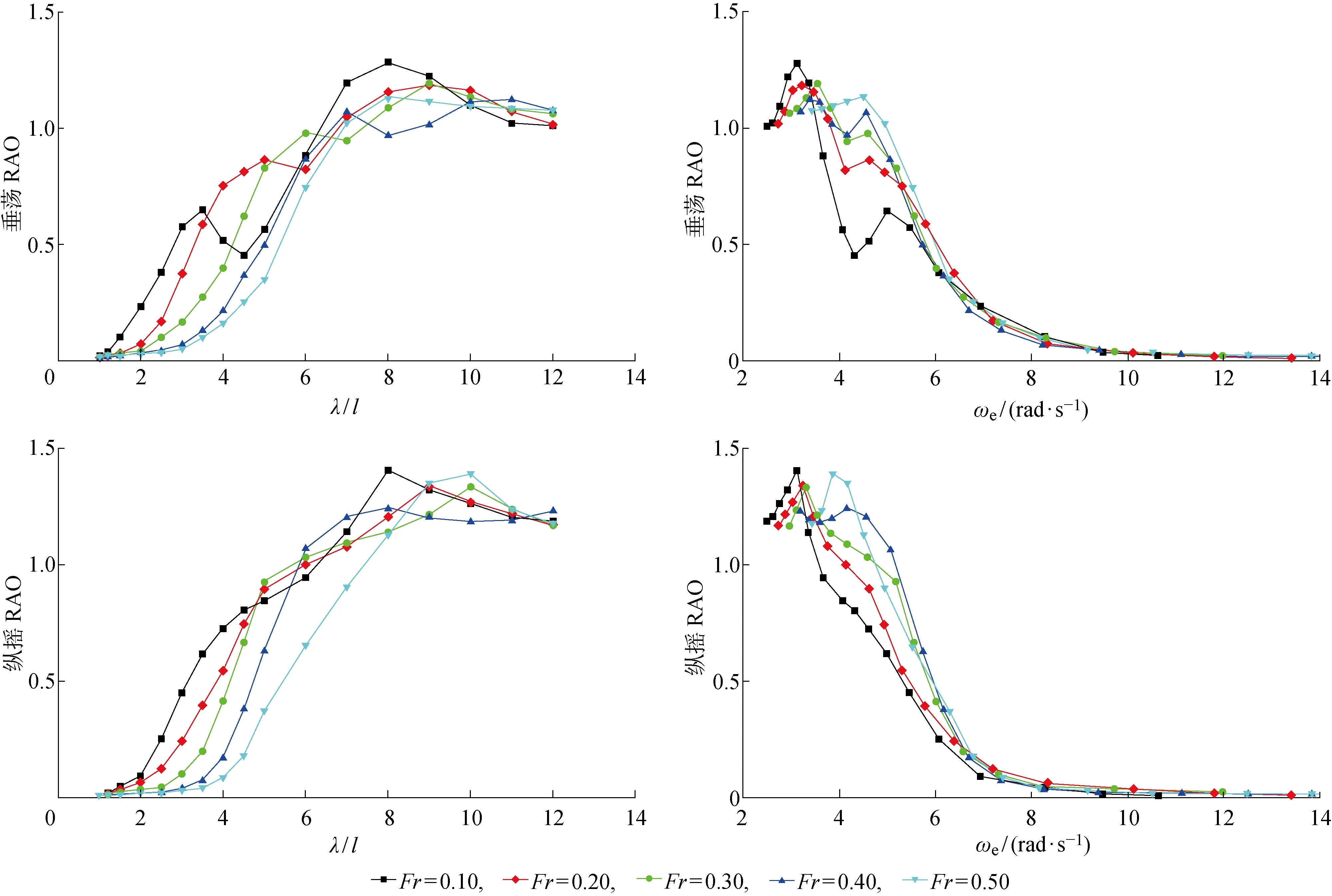
对于所有计算,按照主尺度为1∶10的缩尺比建立长度为2.0 m的船模,相应的计算域及边界条件如图5所示.由于船体的对称性,数值模拟利用边界对称条件只需构建半边船模.计算域的大小在x方向:-5l 图5 计算域及边界条件Fig.5 Computational domain and boundary conditions 作为刚体,为更准确地模拟船体在波浪中的运动,采用重叠网格技术[8].整个计算域分为静止部分(定域)和运动部分(动域),前者是背景网格,后者则为包覆着船体的动网格,嵌套在背景网格中.相比动网格技术,重叠网格在处理大幅度运动时更具有优势.由于不需要重新生成网格,所以不会出现负体积等动网格的缺点,同时相对于沉浸边界法而言,具有更好的计算精度.网格数量约为3×106个,网格的划分细节如图6所示.在船体、自由面及动域附近都进行局部加密,船体表面设置边界层以模拟湍流边界,其他远域网格尺寸相对较大以节省计算时间[16]. 图6 重叠网格划分Fig.6 Overset meshes 计算域的入口速度设置为基于船长的Fr,出口为静水压力边界条件;由于船体对称,中心平面可视为对称面;船体表面为不可滑移壁面,底面及远域壁面均设置为自由滑移壁面,顶部为具有恒定大气压的开阔边界;计算时间步长取Te/200(Te为波浪遭遇周期). 基于RANS方程的数值模拟获得的静水总阻力(Rt)结果与文献试验数据[16]进行对比,结果如图7所示,其中R=Rt/(Vρα),此处α=1.数值计算结果中的摩擦阻力(Rf)是通过对船体表面的切向力求和获得的,剩余阻力 (Rr)是通过对船体表面法向力在船舶前进方向求和获得的.船模试验结果中的摩擦阻力是利用1957年国际船模试验水池会议(ITTC)上提出的公式计算获得的[4],剩余阻力是由总阻力减去摩擦阻力获得的. 由图7可知,2种方法得到的摩擦阻力吻合得较好,而剩余阻力之间存在着较大的误差.在所计算的Fr范围内,摩擦阻力随着Fr的增加而增加.当0.1 图7 I-SWATH船的静水阻力曲线Fig.7 Resistance curve of I-SWATH ship in calm water 不同航速下,对应船体周围的兴波轮廓图如图8所示.由图8可知,当Fr=0.48,0.60时,船体后方的兴波更为严重;而当Fr=0.72时,兴波相对较小.对于水面船舶,兴波阻力通常是剩余阻力的主要组成部分.因此,较大的兴波导致阻力增加,而较小的兴波有利于减小阻力.当Fr=0.36时,附近出现阻力谷值,可能是由于此时船舶片体间的有利干扰使得兴波相对较弱,进而导致兴波阻力较小.当Fr=0.48时,由拖模试验与数值模拟得到的船体表面处的自由液面情况如图9所示.由图9可知,二者吻合得较好,可以验证所采用的数值模拟方法捕捉到的自由液面精度较高,能够进一步研究水动力性能. 图8 静水中不同航速下的兴波图Fig.8 Free surface elevation contours of the fixed model in calm water 图9 当Fr=0.48时斜支柱表面的自由液面Fig.9 Free surface elevation along the struts at Fr=0.48 为了进一步探究斜支柱的作用,增加具有竖直面内自由度的数值模拟.为简化问题,模型暂不考虑舵、鳍和桨的影响.不同于模型试验中水池及测量设备等物理条件的限制,数值模拟能够提供更多的工况选择,获得更高速度下的阻力及运动响应计算结果.规则波中数值模拟的工况如表2所示.其中,h为波高;ak=πh/λ为波陡.由数值计算得到的静水及规则波中的阻力及运动结果如表3所示.其中,波浪增阻(Radd)为波浪中的总阻力减去静水总阻力.阻力(Rt、Rf、Rr)、纵倾角(θ)及沉深(η)均取为自计算稳定收敛后的平均值. 表2 数值模拟的工况Tab.2 Cases of numerical simulations 表3 静水和规则波中阻力及运动的数值计算结果Tab.3 The calculated resistance and motions in calm water and in head waves for free model 由表3可知,当Fr=0.30时,静水纵倾角达到峰值,此处静水阻力也出现了局部峰值(见图7).除了当Fr=0.25,0.30,0.35时,波浪增阻出现了负值以外,其他航速下波浪中的阻力均大于静水阻力.波浪中阻力的增加与波高、平均纵倾角及平均沉深的变化是密切相关的.一方面,这些量的改变直接导致了船体湿表面积的变化,进而影响摩擦阻力;另一方面,这些量是船体在波浪运动状态中的一种客观体现,能够影响剩余阻力.当Fr=0.25,0.30,0.35,且波浪条件为λ/l=0.6,1.0时,波浪增阻出现了负值,这可能是由于平均纵倾角和沉深的减小所导致的.但是当波浪条件为λ/l=1.5时,平均纵倾角及沉深都是增大的,波浪增阻依旧出现了负值.这种现象的出现应该与倾斜支柱有关,船体在波浪中做垂荡及纵摇运动时,倾斜支柱的运动形式类似于振动翼的二维摆动而能够利用由波浪产生的推力[13, 18]. 利用快速Fourier变换(FFT)及Fourier级数展开(FS)相结合的频谱细化方法[22]分析计算所得的运动响应时历曲线,获得不同航速下的垂荡及纵摇RAO,如图10所示.由图10可知,运动响应呈现较强的非线性.垂荡RAO随着遭遇频率的变化呈现出明显的双峰值,不同Fr下的两个峰值分别出现在大致相同的两个遭遇频率处(约为3.2 rad/s和4.9 rad/s),且随着Fr的增加,第1个峰值逐渐减小,第2个峰值逐渐增大.随着Fr的增加,纵摇RAOs的峰值大致呈现出先减小后增大的变化趋势. 当Fr=0.10,0.20,0.30时,纵摇RAOs峰值逐渐减小且大致出现在相同的遭遇频率处(约为3.5 rad/s);当Fr=0.40,0.50时,纵摇RAO峰值逐渐增大,但出现在更大的遭遇频率处(约为4.2 rad/s),因此当Fr=0.30附近时,纵摇RAO的峰值存在极小值.而当Fr=0.25,0.30,0.35时,波浪增阻确实出现了负值.这种情况可能与倾斜支柱有关.当船体在波浪中进行垂荡及纵摇运动时,后置的倾斜支柱运动形式类似于振动翼的摆动而能利用由波浪产生的推力,使波浪增阻出现负值.此外在相同波长条件下,较高航速时的垂荡及纵摇RAO反而相对较小,这也符合SWATH船低速时的稳定性不及高速时稳定性好的特点.但从整体而言,这种特殊的SWATH船比常规的双体船具有更良好的耐波性能. 图10 不同航速时的垂荡与纵摇RAOsFig.10 The heave and pitch RAOs at different speeds 本文介绍了一艘具有倾斜支柱的非常规SWATH船,通过数值模拟方法对其在静水及规则波浪中的水动力性能进行了研究.研究结果表明:倾斜支柱在改善耐波性能方面具有一定的优势,并对此进行了相关的分析讨论. (1) 利用考虑黏性阻尼的三维面元法对这种非常规SWATH船在波浪中的运动响应进行频域分析,改善了计算结果的精确度;讨论垂荡及纵摇RAO,为后续的数值模拟提供了波频选取的合理参考. (2) 为了进一步探究该船型的水动力性能,考虑黏性和自由液面,将RANS方程与波浪发生模块及6自由度刚体运动计算模块整合在一起,预测该船在静水及顶浪规则波中的运动和阻力性能.与模型试验的结果进行对比,验证该数值计算法的准确性. (3) 由于其船型的特殊性,该船在波浪的水动力性能方面具有很强的非线性.垂荡及纵摇运动RAO随遭遇频率呈现出双峰值.导致该种现象的原因一方面是由于片体间的干扰,另一方面是由于倾斜支柱的影响,进而导致了该船具有较强的运动非线性,所以对此船型的研究工作必须仔细处理这些非线性性能. (4) 数值模拟结果中出现负值的波浪增阻,表明倾斜支柱可以利用波浪减少在波浪中航行所需的能量.然而,斜支柱的这种功效并不明显,未来还应通过更多的模型实验进一步研究该船型的这一特性.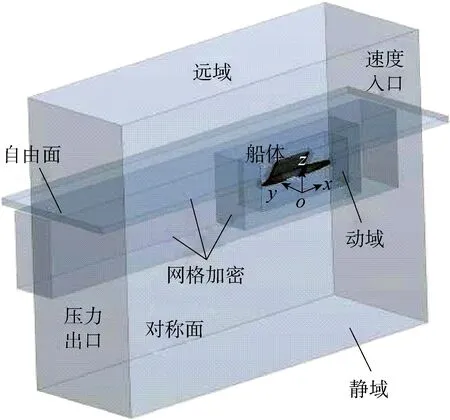
3.3 静水阻力

3.4 静水和规则波中的计算
4 结论
