压缩脆性介质爆破破坏时冲击荷载与初始应力卸载特征

姚颖康， 孙金山， 贾永胜， 吴 亮， 倪明亮， 明 胜， 陈 洋

(1. 中国地质大学 工程学院，武汉 430074； 2. 江汉大学 爆破工程湖北省重点实验室，武汉 430056； 3. 武汉科技大学 理学院，武汉 430081)

爆破是岩石和混凝土等硬脆性材料开挖和破碎的主要方式。岩石类材料爆破破碎时，首先是炸药爆轰在介质中产生冲击波，对介质施加高量级的冲击荷载，形成爆生裂隙；随后，爆生气体进入已生成的裂隙中，使裂隙尖端产生应力集中并驱动裂隙不断扩展、贯通，进一步加剧介质的破碎，最终驱动碎块向临空面方向运动。然而，在高层建筑物的拆除爆破工程中，建筑物底层的立柱在上部荷载作用下将受到较高的初始应力。此类介质或结构在爆破破碎时，与无初始应力介质所经历的受力过程是不同的。

许多学者曾发现爆破过程中初始应力对介质动态响应的影响。如刘殿书等[1]在爆破动光弹实验中，发现模型中较高水平的初始应力对应力波的产生和传播过程产生了显著影响。张志呈等[2]在爆破实验中发现，含初始应力场模型中的爆破振动值远大于实验前的预测值，并认为初始地应力场产生的波导效应造成了爆破振动的增强。张正宇等[3]根据东风水电站地下厂房爆破试验结果，认为爆破开挖过程中初始地应力的卸除对围岩的影响大于爆破荷载的影响。

针对上述现象，国内外学者也曾开展了相关的理论研究。Abuov等[4]研究了隧道岩体爆破开挖时初始地应力快速卸荷对保留岩体的损伤机制；Carter等[5]研究了隧道岩体初始应力的瞬态卸荷在围岩中诱发振动与动应力场。卢文波等[6-7]认为中高地应力条件下岩体爆破开挖引发的围岩振动主要由地应力动态卸载所引起的；孙金山等[8]和祝启虎[9]对高地应力条件下岩体爆破开挖瞬态卸荷引起的围岩松动和损伤效应进行了研究，认为开挖瞬态卸荷在节理裂隙岩体中造成的损伤不可忽视。

然而，由于室内相似模型试验无法模拟实际工程用条状炸药的爆轰过程，对爆破介质的加载和卸载机制难以真实再现。而理论分析模型和数值模型则基于大量假定和简化，研究结果的可靠性往往难以保证。本文通过对建筑物底层立柱的现场爆破实验和一维弹性杆的理论分析，研究了承载混凝土立柱的爆破破坏机制，以及压缩脆性材料爆破时保留部分的加载和卸载特征。

1 压缩钢筋混凝土立柱爆破实验

为研究含压缩应变能脆性介质爆破时保留区的冲击加载与应变释放机制，对建筑物底层钢筋混凝土立柱的爆破过程进行了应变监测分析。

1.1 爆破方案

爆破的钢筋混凝土立柱均位于待拆除建筑物的第一层，爆破部位位于柱的下侧，炮孔布置3排，装填直径32 mm的圆柱状乳化炸药，毫秒延期导爆管雷管起爆。

1.1.1 虹锦公寓工程

虹锦公寓为18层框架结构楼房，如图1所示。一楼结构平面图及试爆立柱位置见图2。立柱混凝土标号为C40，截面尺寸为800 mm×800 mm，受力纵筋为直径22 mm的HRB335钢筋。

图1 虹锦公寓外观Fig.1 Hongjin building

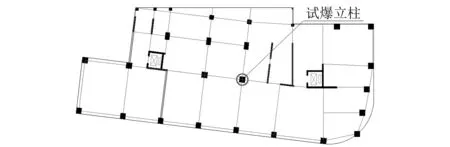
图2 虹锦公寓一楼结构平面图Fig.2 First floor structure of Hongjin building

炮孔直径D=40 mm，炮孔深度L=58 cm。如图3、图4所示。炮孔沿立柱轴向共布置3排，间距b=30 cm。上下排炮孔均为2个炮孔，横向间距267 mm，各装200 g炸药。中间一排3个炮孔，横向间距200 mm，中间炮孔装药200 g，两侧100 g+100 g，空气间隔100 mm。

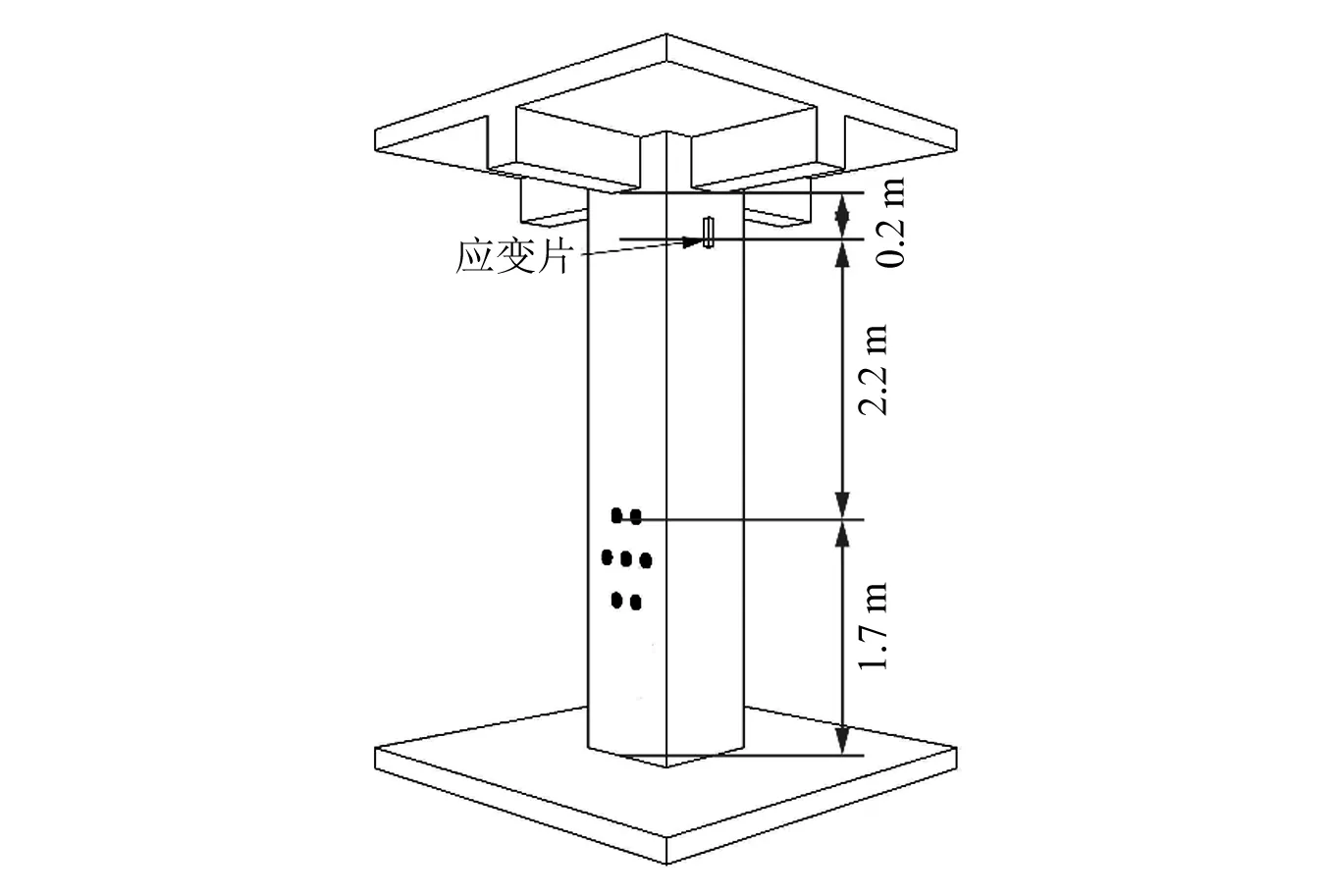
图3 虹锦公寓爆破立柱Fig.3 Blasted column of Hongjin building

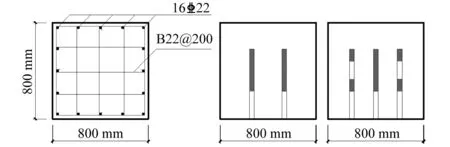
图4 虹锦公寓立柱配筋及装药结构Fig.4 Reinforcement and charge structure of blasted column of Hongjin building

如图5所示，爆破后高度约700 mm范围混凝土受到破坏。其中，炮孔周围的混凝土完全破碎，仅保留弯曲钢筋，竖向受力钢筋最大挠度30～50 mm。混凝土碎块大部分抛出并集中堆积在立柱底部。立柱孔底部分的混凝土局部未完全破碎。

图5 虹锦公寓立柱爆破效果Fig.5 Blasting result of Hongjin building

1.1.2 凯风大厦工程

凯风大厦为12层框架—剪力墙结构楼房，如图6所示。一楼结构平面图及试爆立柱位置见图7。试爆立柱混凝土标号为C40，截面尺寸为500 mm×500 mm，受力纵筋为直径22 mm的HRB335钢筋。

图6 凯风大厦外观Fig.6 Kaifeng building

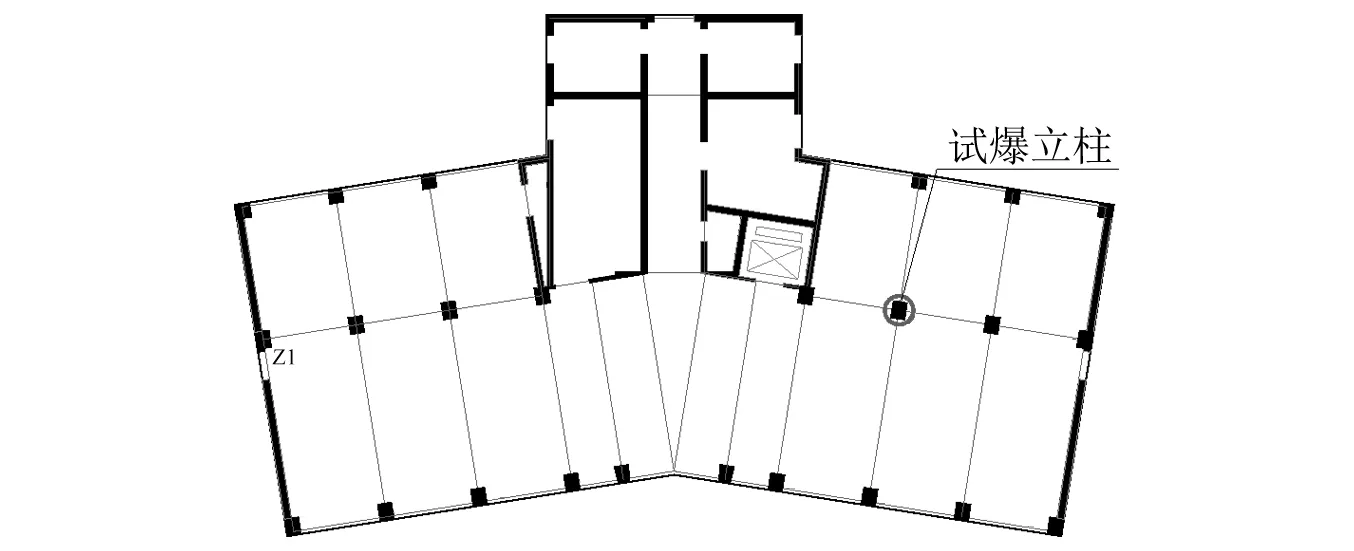
图7 凯风大厦一楼结构平面图Fig.7 First floor structure of Kaifeng building

炮孔直径D=40 mm，炮孔深度L=40 cm，共布置3排炮孔，每排一个炮孔，排距a=30 cm，每孔装药量为130 g。试爆立柱配筋及装药结构如图8、图9所示。

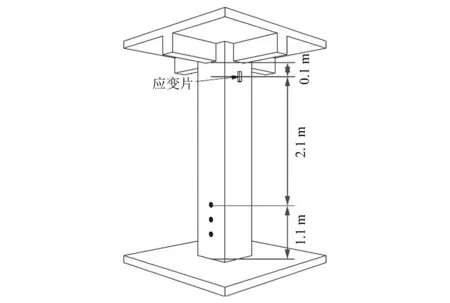
图8 凯风大厦爆破立柱Fig.8 Blasted column of Kaifeng building

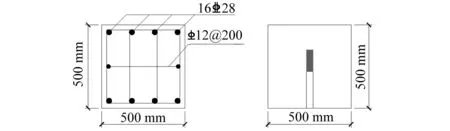
图9 凯风大厦立柱配筋及装药结构Fig.9 Reinforcement and charge structure of blasted column of Kaifeng building

爆破结果如图10所示，爆破范围内大部分混凝土在爆破后被抛出，箍筋被鼓开，竖向主筋发生弯曲，挠度为40～70 mm，混凝土碎块大部分集中堆积在立柱底部，且粒径较大。炮孔底部部分混凝土未完全破碎且未与钢筋剥离。

图10 凯风大厦立柱爆破效果Fig.10 Blasting result of Kaifeng building

1.2 应变监测方案

爆破前在靠近立柱顶部且距离梁底约20 cm处粘贴应变片。虹锦公寓应变测点与炮孔最近距离为2.2 m，凯风大厦为2.1 m(见图3、图8)。

应变片采用50 mm长120 Ω的BX120-50AA混凝土应变片，采用1/4桥连接方式。数据采用DH8302动态信号测试分析系统进行采集，虹锦公寓和凯风大厦实验的采样频率为1 MHz。

1.3 测点总体应变时程特征

通过现场实验，获得了立柱爆破时的监测点的整体应变过程，如图11、图12所示。在该应变时程曲线图中，当立柱充分破碎时，其轴向压力将全部或大部分得到卸载，因此测试得到的混凝土最终应变为拉应变，但其实际处于静力平衡状态。因此，为了反映立柱的真实应变状态，在实测应变曲线中设爆破后立柱的应变为0，则得到了真实的立柱应变时程曲线。

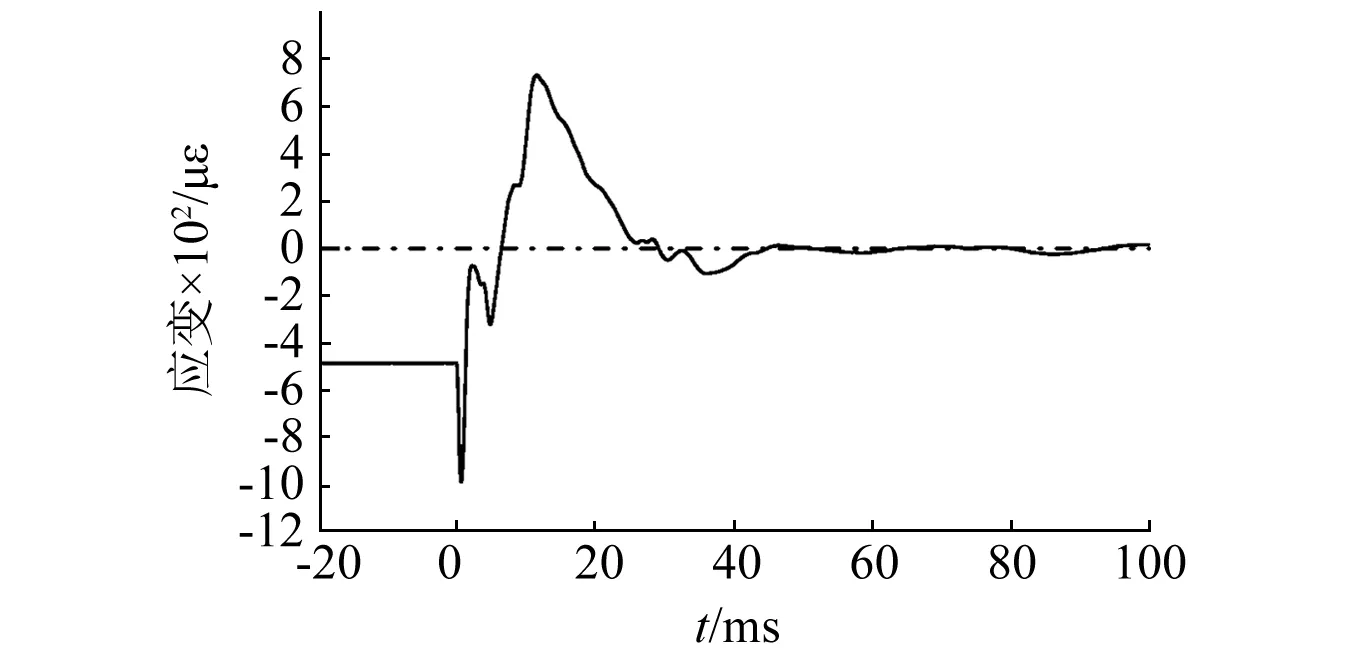
图11 虹锦公寓爆破立柱应变时程曲线Fig.11 Strain history curve of Hongjin building

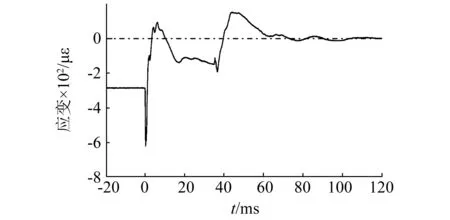
图12 凯风大厦爆破立柱应变时程曲线Fig.12 Strain history curve of Kaifeng building

动态应变测试结果表明，保留区的加载及动态响应过程总体可分为4个阶段：

第一阶段，立柱在上部荷载的作用下，呈轴心压缩或小偏心压缩状态，因此，测点处混凝土初始呈静态压缩状态，具有一定的初始应变值。

第二阶段，炸药起爆后向炮孔壁施加强烈压缩作用，进而对炮孔远区的立柱施加压缩作用。测点处混凝土在原压缩应变基础上急剧增大并迅速恢复至初始应变量。

第三阶段，保留区应变恢复后继续发生相对拉伸应变，直至到达一峰值。在此过程中发生一次波动过程。

第四阶段，达到拉伸峰值后逐渐卸载至0，并经0值附近的多次震波动后恢复至静态。初始存储的弹性能以及爆炸产生的压缩变形能均完全耗散。

其中，凯风大厦应变时程曲线存在2个显著的拉伸峰值，且存在一定的时间间隔，其原因应是爆破时由于雷管延时误差和立柱结构差异，部分结构先破坏后一部分初始应力先卸载，另一部分结构破坏略微滞后，应力发生二次卸载。

2 爆炸荷载加载与卸载特征

炸药爆炸过程极其复杂，炮孔内的压力变化目前无法监测，但许多学者在理论分析基础上，提出了炮孔压力的不同模型，例如指数衰减型荷载模型或三角形荷载模型[10-13]等。实际爆破工程中，多个炮孔对未破坏部位的作用是炮孔压力衰减且相互叠加而成的，它源于炮孔压力，但又不完全相同。在工程实践或理论研究过程中，对炮孔远区荷载的分析是分析结构响应和损伤机制的基础。

2.1 爆炸荷载作用模式

炸药爆炸后，炮孔远区的介质首先受到爆炸加载作用，表现在应变曲线上为一个压缩相的波形，整体呈“三角形”折线(见图11、图12)。

对其放大后发现(如图13、图14所示。设介质的初始应变为0)，其加载与卸载的过程还存在波动并非理想的光滑曲线，且在峰值附近还存在短暂的“平台期”。但整体而言炮孔远区的爆炸荷载作用时程曲线仍大致为三角形的折线形。

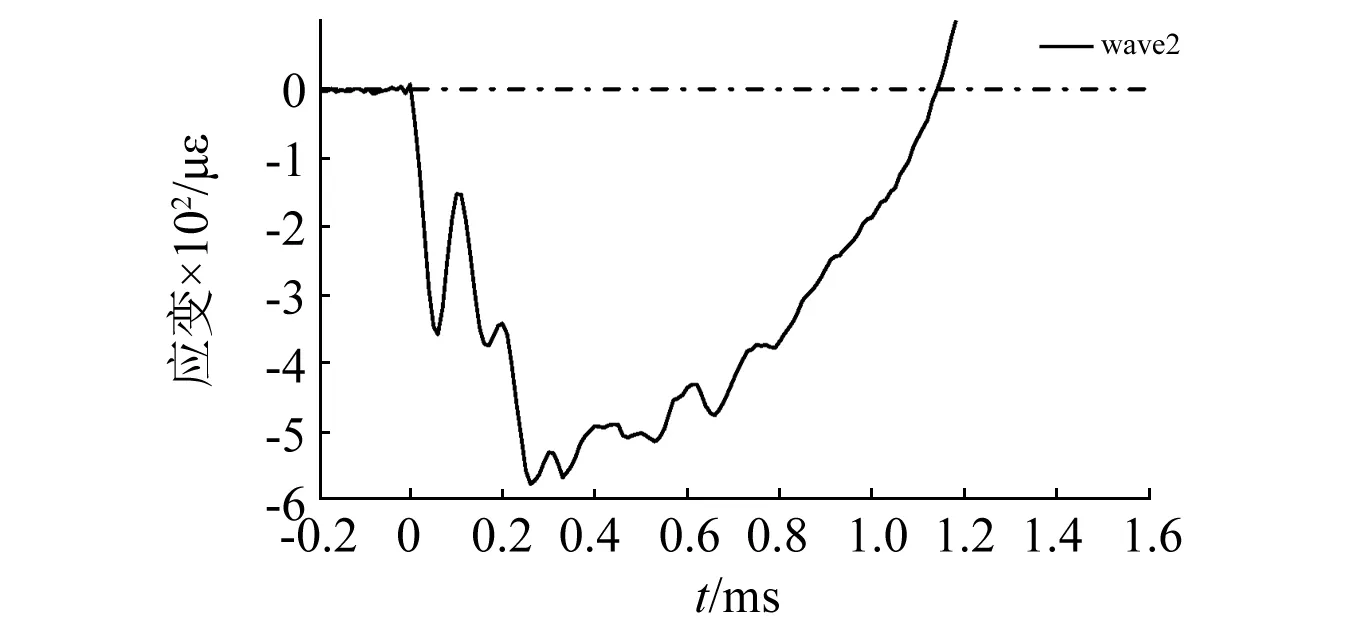
图13 虹锦公寓爆破爆炸附加动应变时程曲线Fig.13 Strain history curve made by shock wave of Hongjin building

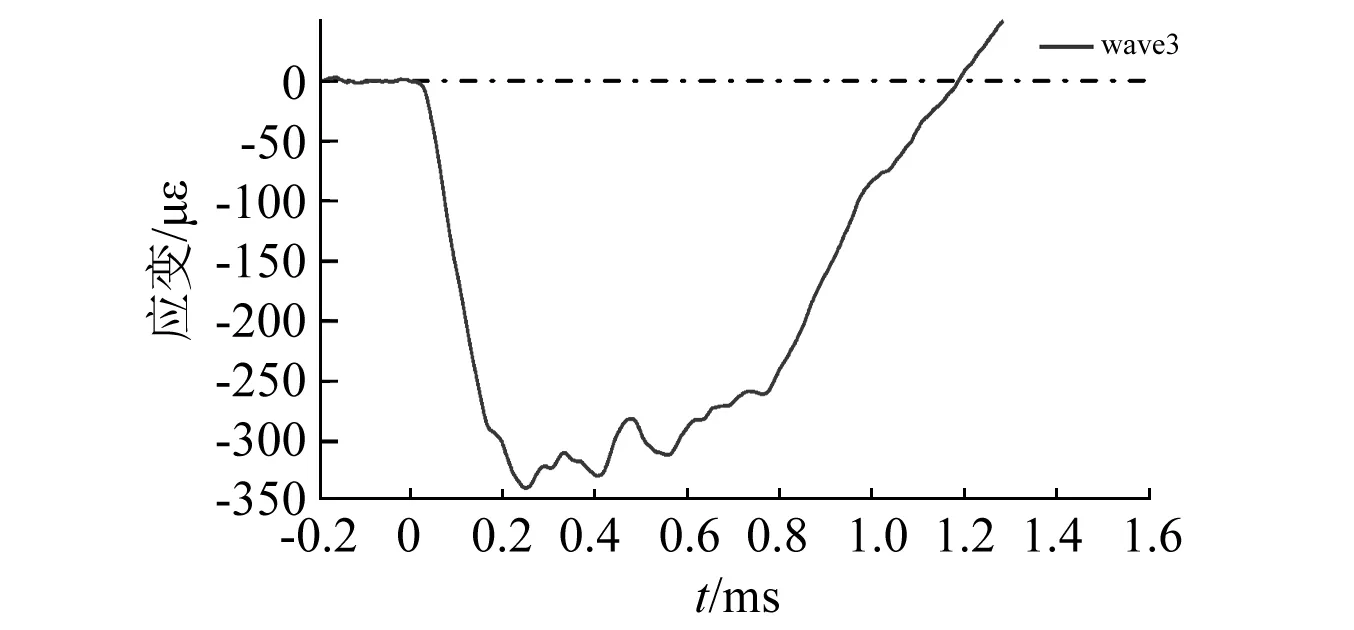
图14 凯风大厦爆炸冲击附加动应变时程曲线Fig.14 Strain history curve made by shock wave of Kaifeng building

2.2 爆炸荷载作用时间特征

炸药爆炸时爆炸荷载的持续作用时间是爆炸作用模拟时的重要参数，许多学者曾通过理论与测试对其进行了研究。如张建华等[14]的计算显示炮腔压力约在几百微秒内衰减；张正宇等[15]认为爆炸应力波持续时间约为10-6～10-1s，爆生气体压力作用时间约为10-3～10-1s。徐国元等[16]爆破实验测试结果显示爆炸应变波持续时间约为20 μs。卢文波等针对柱状装药孔底起爆方式，提出了爆炸荷载作用持续时间的计算模型。目前，针对实际爆破工程中爆炸冲击荷载作用时间的实验研究较少。两次现场实验的监测数据表明(见图13、图14和表1)：

(1)虹锦公寓炮孔同时采用连续装药与空气间隔装药时，爆炸荷载的加载(升压)过程约为0.3 ms，且应变(应力)随时间线性增大，其应变率为1.76 s-1。卸载用时0.9 s，约为加载过程的3倍时间，应变率亦更低，整个过程呈非线性特征。

(2)凯风大厦炮孔全部采用连续装药时，爆炸荷载的加载(升压)过程为0.24 ms，且应变(应力)整体也呈现线性增大，其应变率达到1.44 s-1。爆炸荷载的卸载(卸压)过程相对简单，在达到峰值后略缓慢波动卸载后，立即快速卸压至0。卸压过程历时接近1 ms，卸载过程的应变率为0.37 s-1，低于加载过程。

(3)两次实验中爆炸冲击作用在立柱中产生的最大附加压缩应变约为300～600 με，按照混凝土弹性模量约为30 GPa计算，其在监测点处产生的平均附加压应力约为9～18 MPa。

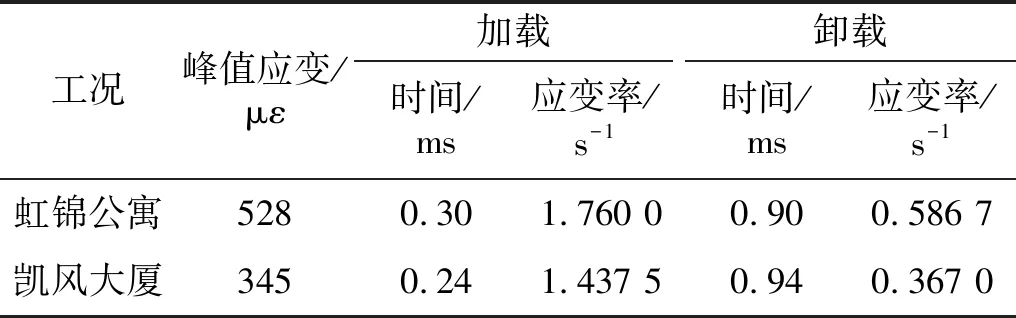
表1 爆炸冲击作用特征参数Tab.1 Characteristic parameters of explosion shock

3 初始应力卸载特征

建筑物底层的混凝土立柱爆破破坏过程中，其自身储存的变形能和初始应力还将发生快速卸载。关于爆破过程中初始应力的卸载过程，有学者认为，在介质充分破碎时，当爆炸荷载升压后再卸压至初始应力的时刻，初始应力开始释放，并假定了直线型、三角函数形和幂函数形的应力卸载函数。但缺乏实测数据的证明。

3.1 初始应力卸载模式

实测应变曲线如图15、图16所示。A阶段为爆炸荷载主要作用阶段，随后出现的B阶段应变曲线接近于A阶段的反射波形，波形接近1/2周期，但周期变大。阶段B的前期应变率接近爆炸冲击卸压过程，而后期的应变率则显著降低。B阶段波动仅根据波形的观察难以解释其发生机制。

在C阶段中，介质的应变以远低于爆破荷载应变率的速率恢复至0值，此时初始应变得以完全释放。该阶段应变时程曲线接近于直线，因此可近似认为初始应力的呈线性卸载模式。

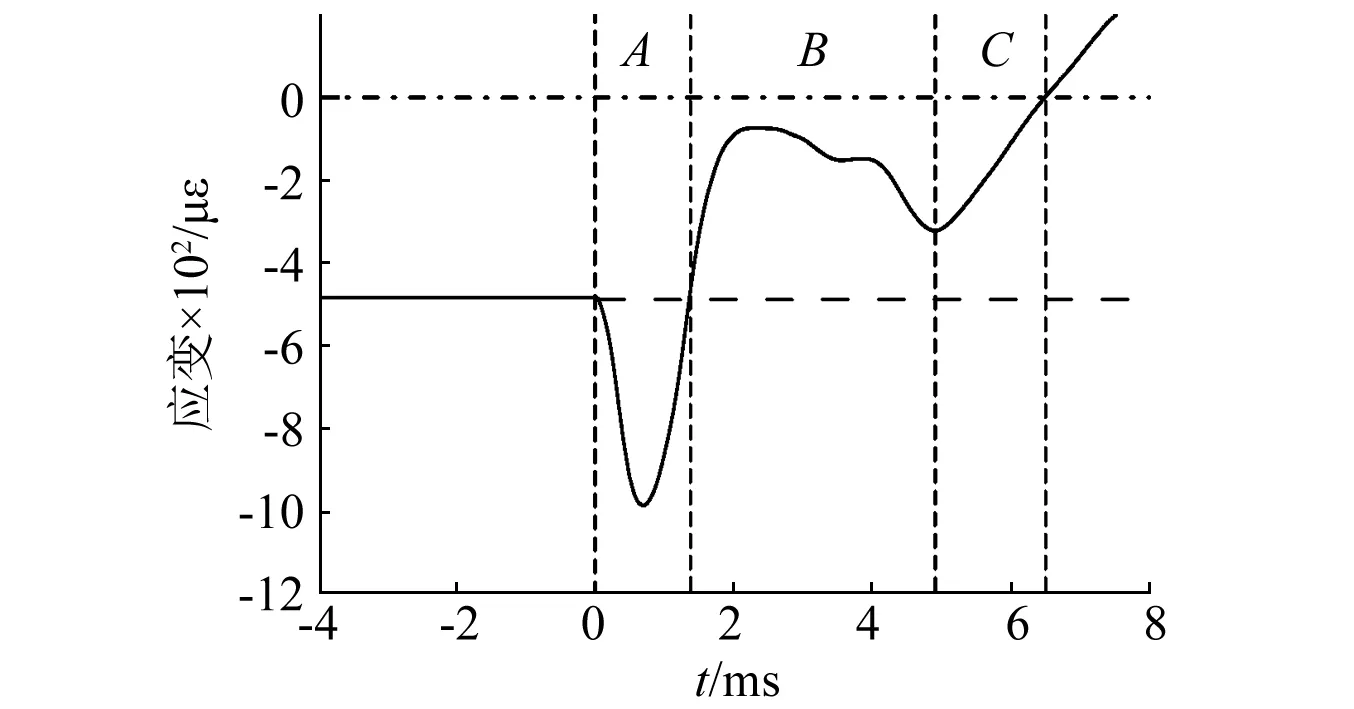
图15 虹锦公寓应变释放时程曲线Fig.15 Strain relief history curve of Hongjin building

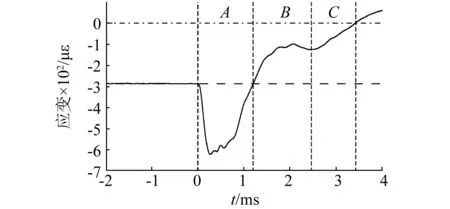
图16 凯风大厦应变释放时程曲线Fig.16 Strain relief history curve of Kaifeng building

3.2 初始应力卸载时间历程特征

测量结果显示，如表2所示。虹锦公寓和凯风大厦的初始压缩应变为483 με和287 με，对应的初始压应力约为14.5 MPa和8.6 MPa。爆破作用结束至初始应变卸载至0时经过的时间tr分别为5.14 ms和2.18 ms，平均应变率为0.093 9 s-1和0.131 4 s-1。

但是，由于无法判断初始应力卸载的真实时刻，卸载的真实时间和应变率难以确定。

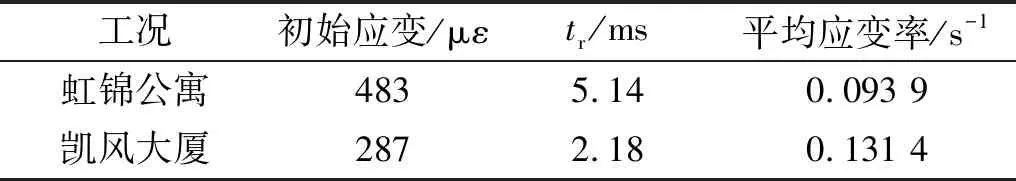
表2 立柱初始应变值与卸载时间Tab.2 Initial strain and unloading time of columns

4 初始应力卸载后的结构响应特征

测试结果如图17、图18和表3所示。当混凝土立柱的初始压缩应变释放至0之后，其应变还将由前期的“压缩相”转化为“拉伸相”，即立柱在达到“中性点”后仍将继续向炮孔方向运动，并在介质中产生“拉应力”。虹锦公寓和凯风大厦的拉应变峰值分别达到732 με和150 με，用时分别为5.02 ms和4.05 ms，对应的应变率为0.145 8 s-1和0.037 0 s-1。而钢筋拉伸荷载随时间的上升和下降均大致呈线性变化。

虹锦公寓的拉伸应变较大，甚至接近初始应变与爆炸冲击应变之和。其原因应是波的反射引起拉应变时，钢筋的弯曲同样也对立柱产生拉伸作用。由于裸露钢筋两端受混凝土约束，爆破作用使其中部弯曲并伸长，造成“拉弓效应”，这使其约束端承受较高的拉伸荷载。由于凯风大厦钢筋数量较少且装药量较小，由钢筋所造成的拉伸作用较弱，其拉应变峰值也就较低。

测点的拉伸应变在达到峰值后，再以较快的速度恢复至0。随后应变幅度迅速衰减，并经历多次振荡，在经过约100 ms量级的时间内基本达到静力平衡状态。

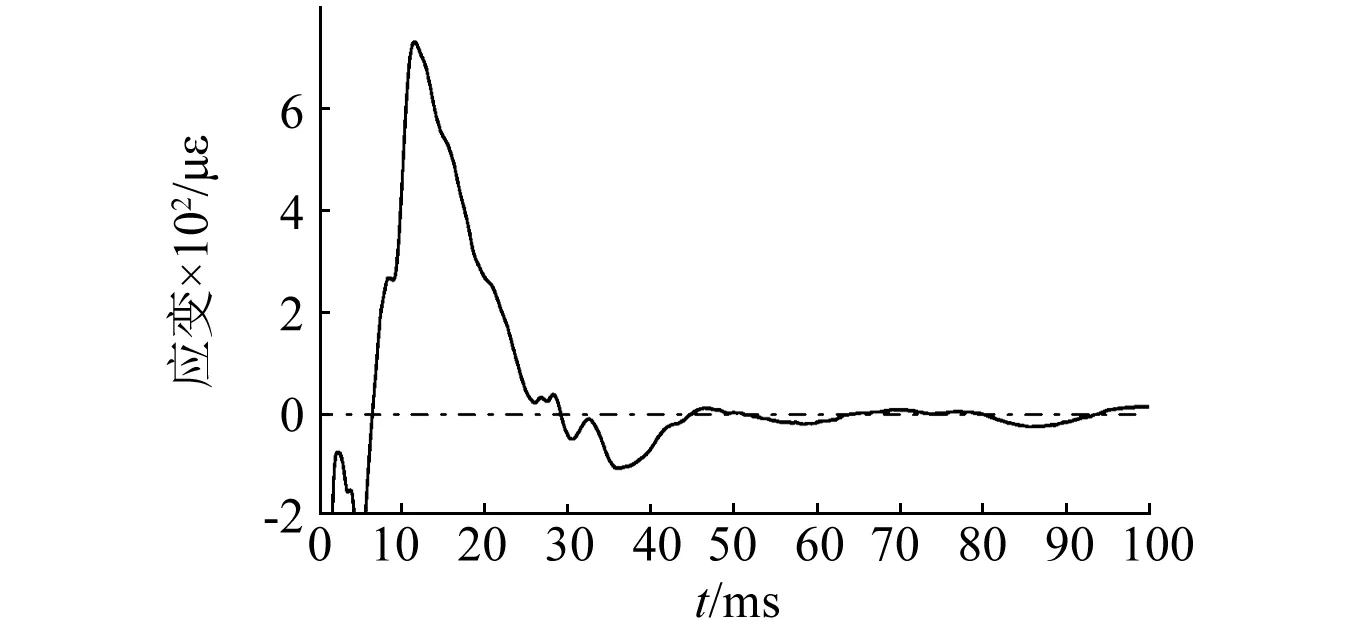
图17 虹锦公寓后期应变时程曲线Fig.17 Late dynamic strain of Hongjin building

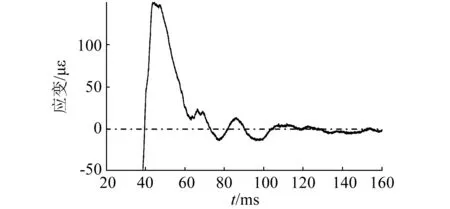
图18 凯风大厦后期应变时程曲线Fig.18 Late dynamic strain of Kaifeng building

表3 动态拉伸过程特征参数Tab.3 Parameters of dynamic tensile process

实验结果如表4所示。由于荷载和结构的差异，立柱后续的应变振荡过程的时间存在一定的差异。如虹锦公寓振荡频率略低，振荡持续时间较长，而凯风大厦表现为较短时间的高频振荡。

表4 应变振荡特征参数Tab.4 Characteristic parameters of strain fluctuating

5 承载立柱爆破破坏过程力学分析

为进一步分析立柱爆破时，初始应力的卸载模式和起始时间，应进一步进行理论分析。由于在炮孔远区，柱状药包产生的柱面应力波相对于立柱较小的截面可近似视为平面波，若不考虑立柱的横向变形，则可采用一维的波动力学模型对实验过程进行近似模拟，以进一步阐释承载立柱的爆破破坏机制。

5.1 冲击作用下一维波动力学模型

如图19所示的不考虑横截面的变形的一维直杆，长度为L，x=0端固定，x=L处端自由，杆端作用有均布荷载P(t)。设直杆的任意截面处，任意时刻的位移为u(x,t)。由于直杆在初始时刻存在轴向压缩初始应力，因此设其杆自由端初始应力为P0，杆中处处轴向应力也为P0，则t=0时刻，由初始应力引起距离固定端x处的初始位移为

(1)

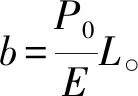
图19 一维直杆力学模型Fig.19 One-dimensional mechanical model of straight bar

为简化分析，直杆的阻尼简化线性黏性阻尼，则直杆质点运动的一维波动方程为[17]

(2)

其中，

(3)

式中：a为纵波波速；E为弹性模量；ρ为密度；μ为泊松比；c为等效阻尼系数。

直杆固定端位移始终为0，即

u(0,t)=0

(4)

t=0时刻直杆任意位置处的速度也为0，即

(5)

直杆自由端受均布压力P(t)作用

(6)

波动力学的求解可转化为齐次边界条件的定解问题，用本征函数展开法求解。设

(7)

将式(6)代入式(1)～式(5)，得

(8)

式(8)可以化为求解问题(Ⅰ)、问题(Ⅱ)的解W1，W2的问题。

(9)

则原方程的解转化为

(11)

解问题(Ⅰ)时，运用分离变量法，令

W1(x,t)=X(x)T(t)

(12)

将式(11)代入式(8)，得

(13)

得

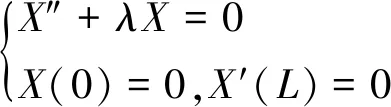
(14)

和

T″+ζT′+a2λT=0

(15)

结合式(9)的边界条件，仅当λ>0时，X(x)有非零解，其固有值为

(16)

相应的固有函数为

(17)

将式(15)代入式(14)得到

T″+ζT′+a2λkT=0,k=1,2,3…

(18)

式(18)是二阶常系数齐次线性微分方程，其解的形式与特征方程t2+ζt+a2λk=0的根有关。令Δk=ζ2-4a2λk，Δk<0,Δk>0和Δk=0时，解的形式有三种情况[18]。Δk<0时为常见的欠阻尼振动情况[19]，得对应的特征根为

(19)

进一步得到

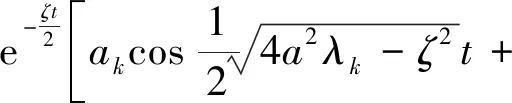
(20)

联立式(12)、式(17)、式(20)，得

(21)

再结合式(9)的2个初始条件，解得

(22)

得

(23)

根据Duhamel原理[20]，若函数φ(x,t,τ)是下列问题(Ⅲ)的解

(24)

则问题(Ⅱ)的解为

(25)

令t′=t-τ，由式(23)得

(26)

式(26)的解法与问题(Ⅰ)相同，得

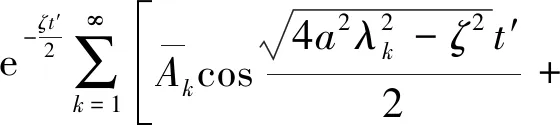
(27)

结合式(26)2个初始条件得

(28)

将t′=t-τ代入式(27)、式(28)，结合式(25)，得

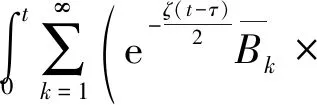
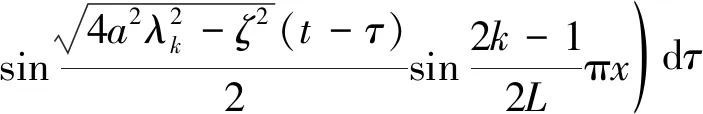
因此，由式(11)、式(23)与式(29)可得原问题的解

(30)

另外，通过对式(30)的解求x一阶偏导，可得到直杆不同位置处的动态应变

(31)

通过数值计算式(30)和式(31)可得到直杆中的位移和应变的近似解。

立柱爆破过程中，除了结构直接受到的加载卸载作用外，还发生动态的响应，因此，在弹性状态下可对爆炸冲击、初始应力释放和钢筋拉伸3个动态压缩和拉伸过程进行叠加，进而得到立柱爆破时非爆破区的动态响应过程。

5.2 动荷载与初始应力释放函数

5.2.1 爆炸冲击荷载函数

根据应变测试的结果，在对计算精度要求不高时，爆炸荷载加载和卸载函数采用三角折线形分段函数，如图20所示。设自由端的荷载函数P(t)，由式(32)表示。

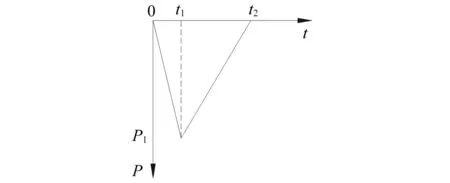
图20 爆炸荷载时程曲线Fig.20 Blast load history curve

(32)

5.2.2 初始应力释放函数

为确定应力释放的模式，假定以如图21和式(33)所示线形卸载函数模拟初始应力的释放过程。初始时刻，自由端在载荷P0作用下产生位移b并处于静止状态。卸载开始时，初始荷载按照函数P(t)线性减小至0。

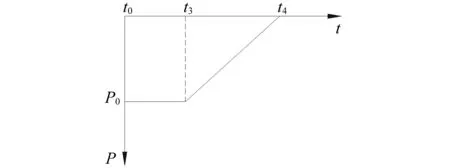
图21 初始应力释放时程曲线Fig.21 Initial stress unloading history curve

(33)

5.2.3 钢筋拉伸荷载函数

根据应变测试结果，立柱混凝土破碎抛掷引起的轴向钢筋拉伸荷载函数T(t)采用三角折线形分段函数，如图22和式(34)所示。

图22 钢筋拉伸作用函数Fig.22 Load history curve of tension caused by steel bars

(34)

5.3 初始应力卸载特征模拟

以虹锦公寓工程爆破立柱为例，设立柱爆破后自由端至固定端(将立柱顶部梁柱节点处近似视为固定约束)的长度为2.4 m，监测点距离自由端2.2 m(距固定端0.2 m)，采用直杆波动力学模型分析监测点处应变过程。

钢筋混凝土立柱的平均密度为2 550 kg/m3，发生爆破损伤后混凝土的弹性模量为25 GPa，泊松比为0.2，阻尼参数ζ取800。

为判断初始应力卸载过程的开始时刻和卸载时长，分别设置Case1和Case2。其中，Case1假定初始应力卸载开始于爆炸荷载作用结束时刻，因而卸载时间较长。Case2假定初始应力卸载滞后爆炸荷载结束时刻3 ms，卸载时间较短。Case1和Case2计算参数如表5所示。

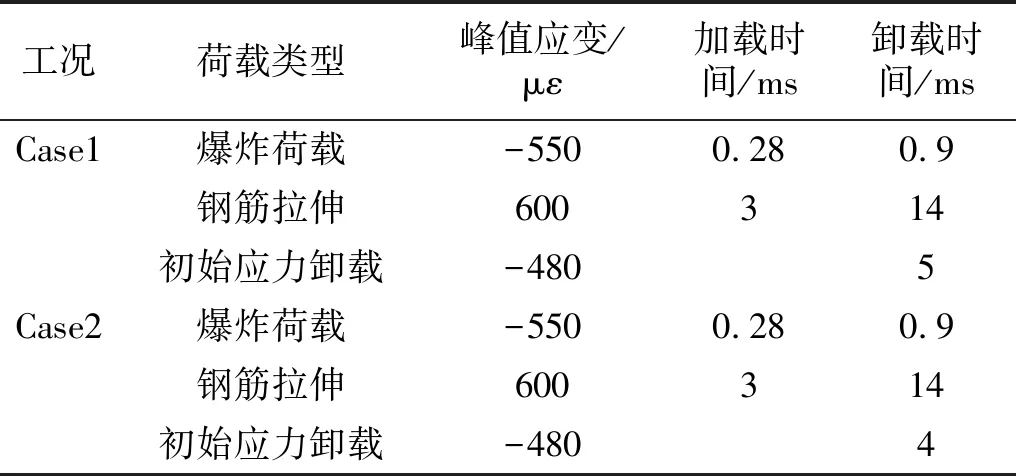
表5 动荷载和初始应力卸载函数参数Tab.5 Parameters of dynamic load and initialstress unloading function

计算结果如图23所示。Case1在70 ms以后的计算结果与实际测试结果偏差较大，峰值点提前出现。而假定初始应力卸载滞后于爆炸荷载结束时刻3 ms的Case2更接近于实验结果。

因此，初始应力的卸载是在爆炸冲击波强烈作用消失一段时间后才开始的。而该段滞后的时间，应是破碎混凝土逐渐向水平方向移动所经历的时间。该过程使结构的初始承载力下降或消失，也为初始应力卸载所需的轴向变形提供了“位移空间”。而初始应力是在较短时间内以线性模式进行卸载的。

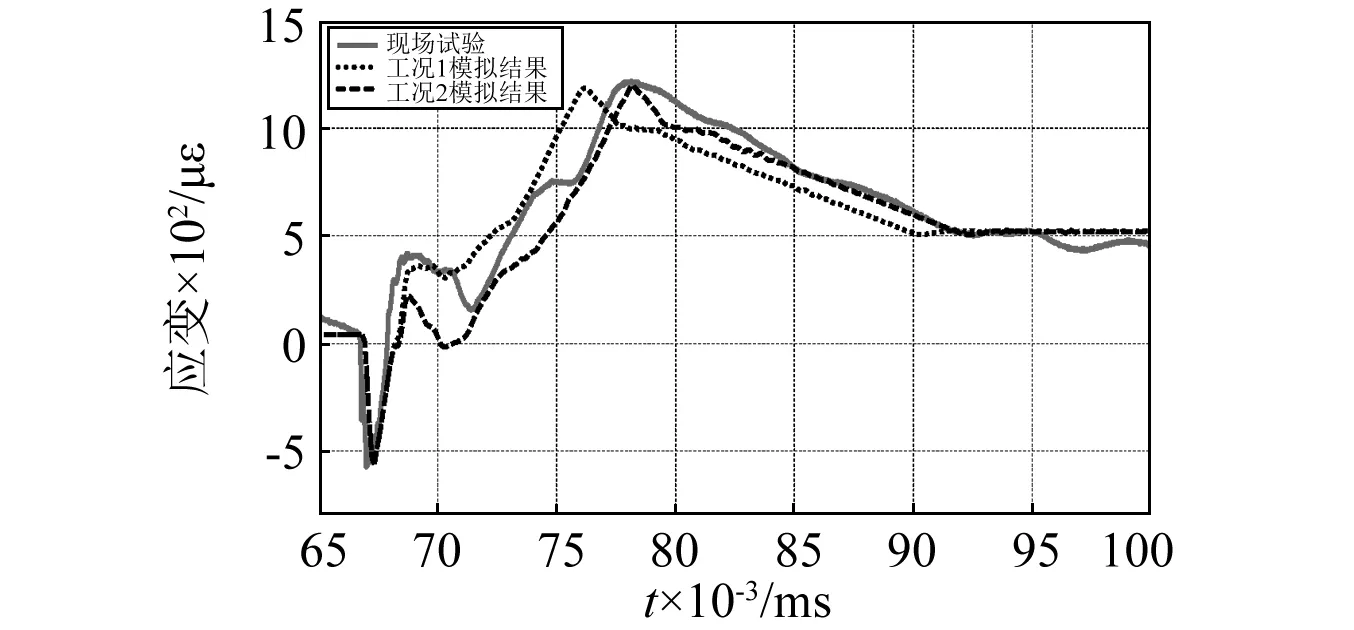
图23 虹锦公寓应变模拟结果Fig.23 Calculated strain history curve of Hongjin building

5.4 承载立柱爆破受力与响应历程

对立柱爆破时保留区应变过程的模拟结果表明，含压缩变形能脆性介质的受力和破坏过程可分为以下几个过程：

(1)炸药在炮孔内起爆后，爆轰产生冲击波并随着孔壁的粉碎而迅速降低。冲击波和应力波在炮孔近区和远区中引起强烈的压缩应变。

(2)爆炸冲击波和应力波强烈作用消失后，爆生气体的体积膨胀产生相对较弱的荷载。且在其作用下裂纹进一步扩展与贯通，但该阶段介质仍具有完全的承载力。

(3)由于破碎介质的运动速度远低于爆炸冲击波和应力波的传播速度，因此破碎混凝土块在炸药起爆一段时间后才开始发生抛掷飞散。伴随着碎块的运动立柱承载能力迅速消失，其初始应力同样随之迅速卸载，而储存的应变能则应转化为振动能和破碎能。

(4)破碎混凝土的飞散使箍筋松脱和竖向钢筋发生侧向弯曲，并对保留的未破坏部分施加强烈拉伸作用。最终，爆炸作用消失后立柱保留区恢复至静力平衡状态。

6 结 论

基于虹锦公寓和凯风大厦钢筋混凝土立柱现场爆破实验，以及爆炸加载和卸载机理的理论分析，得到以下结论：

(1)实际工程爆破中，每次炸药爆轰在炮孔远区产生的爆炸荷载时程曲线大致呈三角形折线状，其爆炸荷载升压阶段应变率高于卸压阶段。

(2)爆炸冲击波和应力波作用消失后，在爆生气体作用下爆破介质裂纹扩展、贯通，但该阶段承载力不发生降低，此时结构中附加动应变较小且初始应力不卸载。

(3)当介质完全爆破破碎且抛掷飞散时，其承载能力迅速消失，初始应力随之卸载。且卸载起始时刻滞后于爆炸荷载结束时刻一段时间，该段滞后的时间，是破碎混凝土向水平方向移动所经历的时间。初始应力卸载的时程曲线接近于直线形，其卸载的应变率较低。

(4)破碎混凝土的飞散使钢筋混凝土立柱轴向受力钢筋发生侧向弯曲，使未破坏部分受到强烈轴向拉伸荷载。