统计问题常见考题例析

■胡 彬

统计是高中数学的重要内容,在历年高考中占有重要地位,题型多以解答题为主。下面对这类题型举例分析。

例1某学校为了解1000名新生的身体素质,将这些学生编号为1,2,…,1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验。若48号学生被抽到,则下面4名学生中被抽到的是( )。

A.9号学生 B.207号学生

C.718号学生 D.815号学生

解：由系统抽样可知,第1组学生的编号为1到10,第2组学生的编号为11到20,…,最后一组学生的编号为991到1000。设第1组抽到的学生编号为x,则第2组抽到的学生编号为x+10,以此类推,可知所抽取的学生编号为10的倍数加x。因为48号学生被抽到,所以x=8,由此可知718号学生被抽到。应选C。

评注：解决系统抽样的两个关键点是：①分组的方法应由抽取比例而定;②起始编号确定后,其他编号随之确定。

例2某城市100户居民的月平均用电量(单位：度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图1所示。

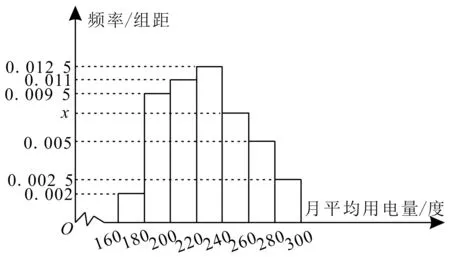
图1

(1)求直方图中x的值。

(2)求月平均用电量的众数和中位数。

(3)月平均用电量在[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?

解：(1)由已知可得20×(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)=1,解得x=0.0075。

(2)由频率分布直方图可知,面积最大的小矩形对应的月平均用电量所在的区间为,所以月平均用电量的众数的估计值为230。

因为20×(0.002+0.0095+0.011)=0.45＜0.5,20×(0.002+0.0095+0.011+0.0125)=0.7＞0.5,所以中位数在区间[220,240)内。设中位数为m,则20×(0.002+0.0095+0.011)+0.0125×(m-220)=0.5,解得m=224,所以月平均用电量的中位数的估计值为224。

(3)由频率分布直方图可知,月平均用电量在[220,240)的用户数为(240-220)×0.0125×100=25。

同理可得,月平均用电量在[240,260),[260,280),[280,300)的用户数分别为15,10,5。

由题意可知,用分层抽样方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取的用户数为

评注：本题主要考查频率分布直方图的实际应用问题。