木板抓取机器人手眼标定方法

徐呈艺 刘 英 贾民平 肖 轶 曹 健

(1.南京林业大学机械电子工程学院， 南京 210037； 2.南通职业大学机械工程学院， 南通 226007；3.东南大学机械工程学院， 南京 211189)

0 引言

目前，铺地板的方式主要是人工铺放，存在劳动力少、成本高等问题。随着机器人技术高速发展，通过机器人视觉系统完成该项工作具有较好的实用意义，目前尚未发现有相关文献或报道。手眼标定是机器人末端正确定位、完成木板抓取的关键。机器人视觉伺服控制系统中机器人和相机的关联方式，即手眼关系，主要有两种：眼在手外(Eye-to-Hand)和眼在手上(Eye-in-Hand)。Eye-to-Hand方式中相机固定，具有简单、方便等优点，主要用于固定区域目标的定位或识别[1]。Eye-in-Hand方式是在机器人手臂末端安装相机，相机随着机器人手臂末端一起运动，赋予机器人主动视觉功能[2-3]。确定机器人执行末端与相机的相互位姿变换关系，需要手眼标定[4]，该技术直接影响到机器人视觉伺服控制功能的精确实现。

手眼标定方法主要分为需要标定参考物和不需要标定参考物两大类。不需要标定参考物的方法标定复杂，受干扰因素多[5-7]。需要标定参考物的传统方法是运行机器人使其末端带动相机，以两种位姿观测同一标定参考物，整合两组采集结果，获得一个标定方程。手眼标定法求解的非线性和不稳定性问题一直是机器人视觉伺服领域的研究热点之一。主要求解方法有：文献[8-11]基于传统标定方程推导了经典求解两步法；文献[12-16]对传统标定方程进行了变换，同时求解了旋转矩阵和平移向量；还有少部分研究[17-18]对标定方程进行了改进再求解。

本文以机器人带动相机采集一次数据获得一个标定方程，采用Kronecker product算法和最小二乘法对多个标定方程进行求解，并用Levenberg-Marquardt算法对其进行优化，通过仿真平台的可视化模块验证该标定方法的有效性。在不同噪声水平和采集图像数量下运行机器人、观测标定板，并对求解得到的标定方程与传统标定法进行比较。最后进行木板视觉抓取试验，验证整体视觉系统精度。

1 传统手眼标定方法

图1 传统手眼标定方法模型Fig.1 Hand-eye calibration model with traditional model

传统标定方法是将两种位姿构成一个闭环回路关系，有

(1)

即

CX=XD

(2)

其中

式中C——相机坐标系在机器人运动前后的位姿变换关系

D——机器人末端坐标系在机器人运动前后的位姿变换关系

X——相机坐标系到机器人末端坐标系的位姿变换关系

即所求手眼关系转换成对CX=XD的问题进行求解。

2 基于标定方程的求解及优化

2.1 标定方程建立

(3)

即

AX=ZB

(4)

通过采集一系列数据(A，B),计算相机与机械手上的相对位置X，可直接求解AX=ZB。

图2 手眼标定方法模型Fig.2 Hand-eye calibration method model

2.2 标定方程的求解

A、X、Z、B为4×4的齐次矩阵，式(4)则可写成旋转矩阵(姿态)和平移向量(位置)，即

(5)

展开式(5)，则第i次采集的数据满足

RAiRX=RZRBi

(6)

RAiTX+TAi=RZTBi+TZ

(7)

(8)

可利用Kronecker product算法求解RX与RZ，根据Kronecker product性质，式(8)可变换为

(RBi⊗RAi)9×9vec(RX)=vec(RZ)

(9)

将式(9)变换为

(10)

如果有n组数据，利用最小二乘法计算，可得

(11)

其中

解得旋转矩阵RX与RZ后，可解平移向量TX与TZ，由式(7)得

RAiTX-TZ=RZTBi-TAi

(12)

将式(12)变换为

(13)

同样用最小二乘法求解得到平移向量TX、TZ，得到标定结果。

2.3 标定结果的优化

上述求解方法分开求解姿态和位置，姿态部分的误差会传递到位置，从而可能造成标定精度下降。本文采用Levenberg-Marquardt算法对其进行优化。对标定的求解过程作为优化算法的一个初始化过程，结果作为优化算法的初始值。采用迭代方式降低误差函数值。由式(4)得

B=YAX

(14)

其中

Y=Z-1

同样式(14)可写成旋转矩阵(姿态)和平移向量(位置)表示形式，即

(15)

对式(15)展开可得

(16)

建立误差函数为

(17)

其中

p=(nX1,nX2,nX3,nY1,nY2,nY3,TX1,TX2,TX3,TY1,TY2,TY3)

建立雅可比矩阵J和误差向量ε为

(18)

(19)

其中

Jfi=

利用Levenberg-Marquardt算法在基于Kronecker product算法与最小二乘求解的初值基础上进行迭代运算可得最优结果[21-22]。

3 试验及分析

3.1 数据采集

在ROS仿真系统中，采用标准的棋盘格标定板并固定放置Motoman SDA10型双臂机器人，即机器人基坐标系不动，编程控制机器人左臂末端带着需要标定的相机从不同视角拍摄标定板进行数据采集，机器人不同动作下获取的图像和本身关节角自动保存，其中采集图像如图3所示。

采集状态的机器人运动学正解结果如表1所示，x、y、z表示位置分量；ow、ox、oy、oz是四元数表示的姿态分量。

对应机器人运动的16组状态，通过张正友相机标定法得到相机标定外参，即标定板世界坐标系到相机坐标系位姿变换关系矩阵A如表2所示。

3.2 标定结果验证

利用Kronecker product算法与Levenberg-Marquardt迭代得到手眼标定最终结果为

图3 采集的图像Fig.3 Collected images

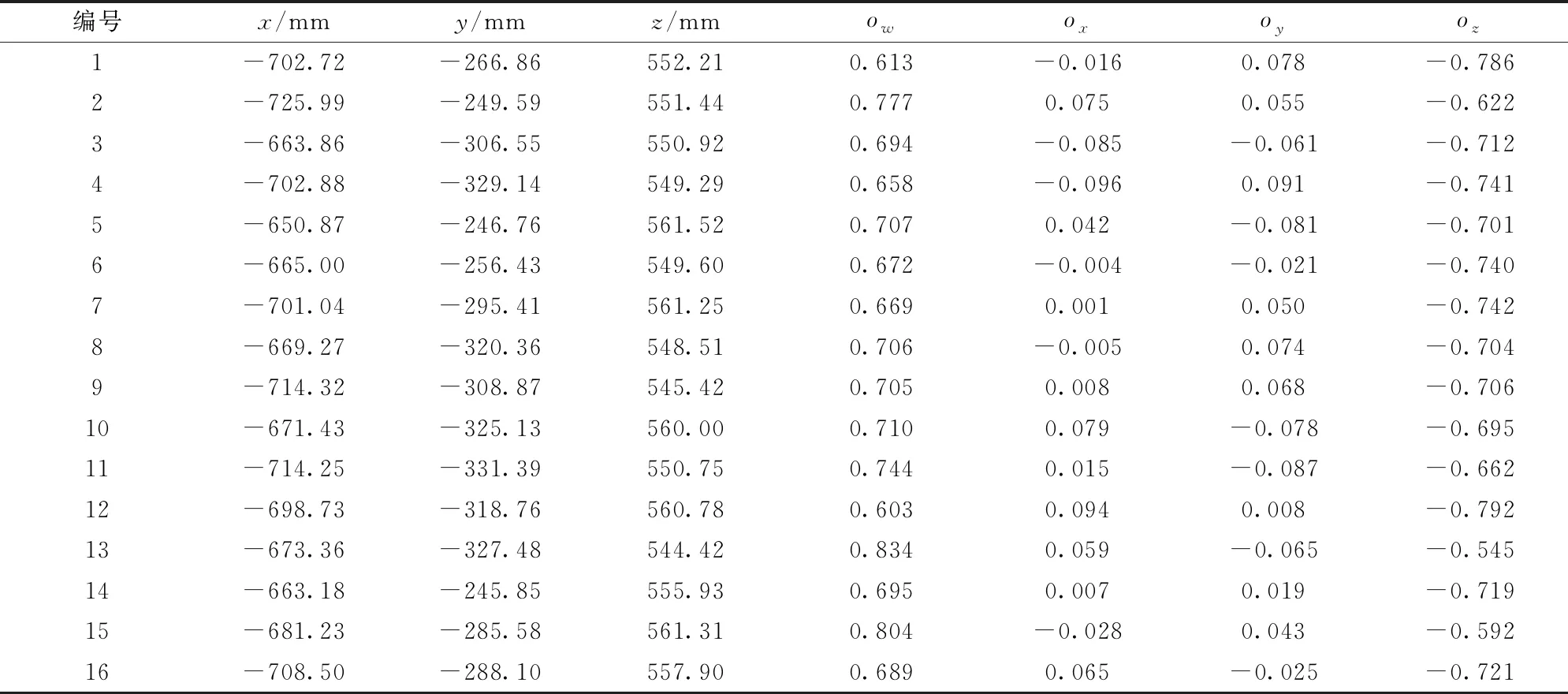
表1 16组机器人运动学正解(矩阵B)结果Tab.1 16 groups of forward solution (B matrix) results of robot kinematics

表2 16组标定板检测(矩阵A)结果Tab.2 16 groups of calibration plate detection (A matrix) results

基于标定结果将深度相机得到的点云数据直接投影到ROS系统3D可视化工具Rviz中，如图4所示，点云与机器人的模型完全匹配，无错位现象。给定单块木板在机器人基坐标系下的位姿，可知木板模型的点云相对于机器人基坐标系的位置向量p，另控制机器人带动相机以不同位姿对单块木板进行观测并获得一系列点云数据，由机器人正运动学与本文手眼标定算法求得该点云在机器人基坐标系下的位置向量q，并与对应p求得平均欧氏距离即点云匹配误差为0.1 mm数量级，说明标定结果有效，符合要求。

图4 标定结果可视化Fig.4 Visualization of calibration results

3.3 标定结果精度分析

手眼标定的误差与机器人本体、相机标定和标定方程求解方法等都有直接关系。而机器人本体末端定位精度主要跟关节角相关，相机标定误差跟标定模型及外部因素相关，相机标定模型采用张正友经典算法[19]，外部因素主要有拍摄标定板图像数量与特征点提取精度[23]。因此用新标定方法和传统标定方法对不同噪声水平下的标定结果进行对比，用同样的两种方法对不同采集图像幅数的标定结果进行对比。

考虑到MOTOMAN SDA10型机器人重复定位精度为±0.1 mm，给机器人各关节变量加入期望为0，均方差为σ1的高斯噪声，其中σ1为[0.002，0.02]区域10等分的不同值。对机器人带动相机采集的图像加入期望为0，均方差为σ2的高斯噪声，其中σ2为[0.02，0.2]区域10等分的不同值。对10组σ1和σ2依次配对组成噪声水平试验组进行标定，标定仿真过程及分析如下：

(1)给机器人7个关节角加入第a组噪声水平，运行机器人带动相机以多种位姿观测标定板图像，如图5所示，得到12幅采集图像。同时根据机器人正运动学方程可得12个变换矩阵Bi。

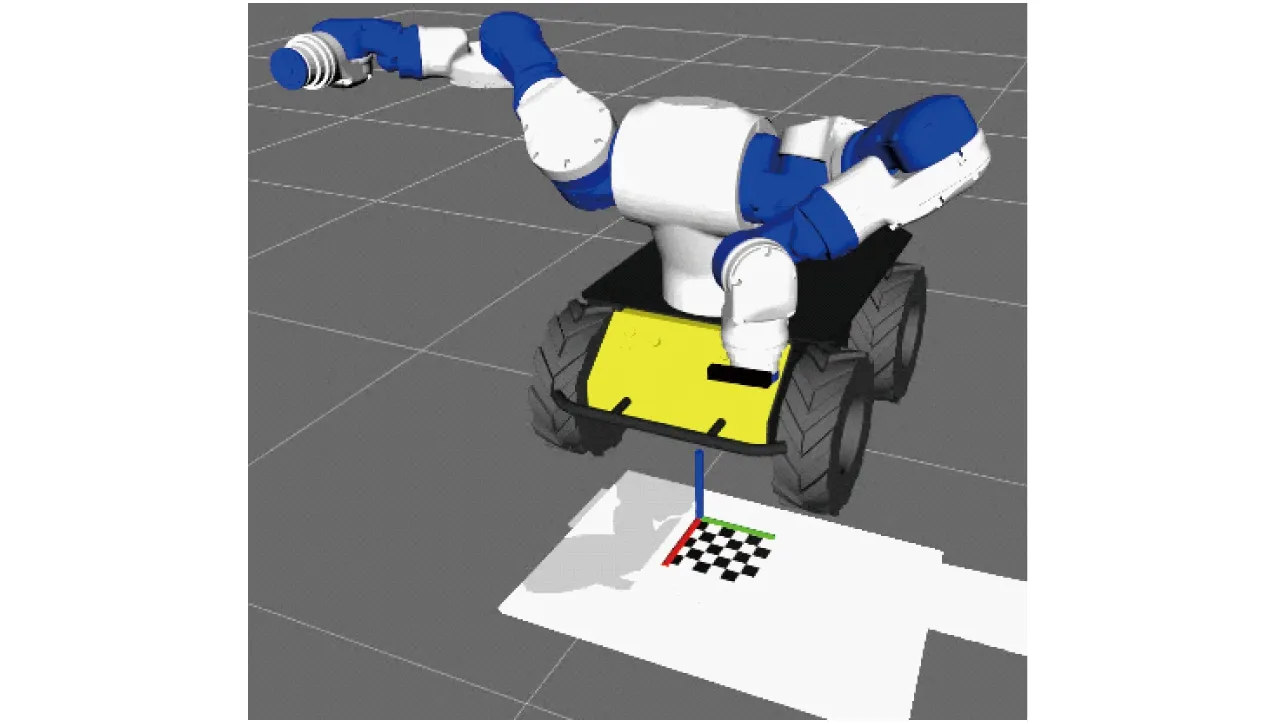
图5 手眼标定数据采集试验Fig.5 Hand-eye calibration data acquisition test

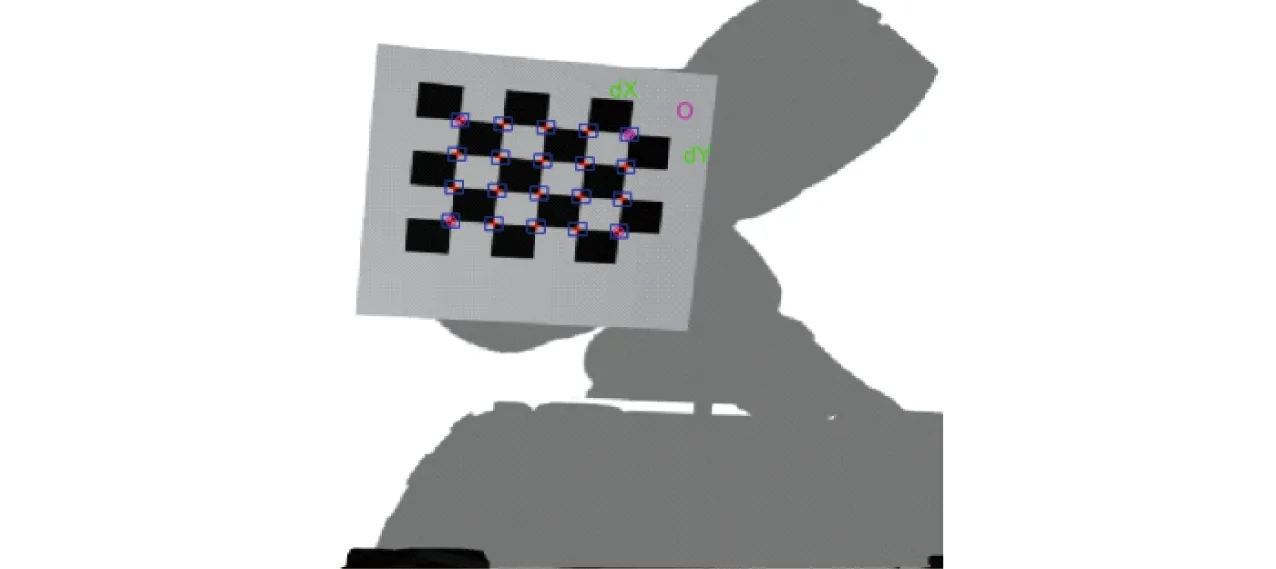
图6 角点提取效果Fig.6 Corner point extraction effect

(2)对相机拍到的标定板图像加入第a组噪声水平，对图像采用Harris角点提取，效果如图6所示，由相机标定张正友法[19]求得12个变换矩阵Ai。

(3)使用本文方法得到12个标定方程并求解优化Xa，与给定的值X′建立位置向量绝对误差，以上独立进行600次试验，平均位置误差算式为

(20)

式中t(·)——取变换矩阵的位置向量部分

采用Tsai传统标定法得到6个标定方程，求解并得到与给定值的位置绝对误差，标定结果误差如图7所示。

图7 标定结果误差与噪声水平关系Fig.7 Relationship between calibration error and noise level

(4)使用同一噪声水平试验组σ1～σ2，针对不同的图像数量，利用上述流程进行试验，标定结果误差如图8所示。

图8 标定结果误差与图像数量关系Fig.8 Relationship between calibration error and image quantity

由步骤(3)数据可知，同样数量的采集数据组，手眼标定方法所获得标定方程比传统方法多，本文手眼标定法平均精度为3.17 mm，传统手眼标定法平均精度为4.45 mm，本文方法相对传统法精度平均提高了30%，随着噪声水平的增加，本文算法优势愈加明显；由步骤(4)可知，同一噪声水平下，标定精度随着采集数据组数目增加而提高，本文手眼标定法平均精度为1.36 mm，传统手眼标定法平均精度为2 mm，本文方法相对传统法精度平均提高了31.1%，采集图像数量越多，精度越高，但在12幅以后，标定结果趋于稳定。

3.4 木板抓取试验

木板抓取流程为：

(21)

(4)由机器人逆运动学实现抓取木板。

将木板放置给定的不同位姿，进行抓取试验，如图9所示，利用本文算法求解机器人抓取木板时定位位置与给定位置求欧氏距离得到其定位精度，并与传统方法相比较，设置木板放置的不同位姿数量分别为50、100、200、500等，定位精度如表3所示，传统标定法平均视觉定位精度为2.864 mm，本文方法平均视觉定位精度为1.739 mm，应用本文方法的视觉定位比传统方法精度平均提高了39.2%，抓取成功率为96.2%，部分失败的原因是木板放置在机器人关节极限范围以外。

图9 木板抓取试验Fig.9 Picking board test

表3 机器人视觉抓取定位精度Tab.3 Robot visual picking position accuracy

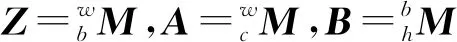
4 结论

(1)该标定方法以机器人带动相机采集一次数据，即可获得一个标定方程，利用Kronecker product算法和最小二乘法对标定方程进行求解，得到的解作为初始值，建立了雅可比矩阵和误差函数，利用Levenberg-Marquardt算法对其进行优化，通过ROS系统中的3D可视化工具Rviz验证了标定结果的有效性。

(2)本文方法在手眼标定本身求解精度和应用机器人整体视觉系统定位精度方面相对于传统方法有一定的提高。相同采集图像数量、不同噪声水平下，本文标定方法位置解精度比传统标定方法平均提高了30%；相同噪声水平、不同采集图像数量下，本文标定方法位置解精度比传统标定方法平均提高了31.1%。机器人视觉系统抓取定位精度比传统标定方法平均提高了39.2%，木板抓取成功率为96.2%。