高效粒子群算法研究及飞翼无人机气动隐身优化设计

樊华羽，詹浩，程诗信，米百刚，姚会勤

(1.西北工业大学 航空学院，西安 710072) (2.清华大学 航天航空学院，北京 100084)

0 引 言

飞行器外形多目标优化设计是一个跨学科多目标的优化任务，包含了总体、气动、结构、隐身等多个领域和专业的关键技术。这些因素之间相互交叉干扰，进一步增加了现代飞行器多目标优化设计的复杂性。随着电子计算机技术的蓬勃发展和计算流体力学(CFD)、电磁计算精度的提高，数值优化算法结合先进的CFD与电磁计算，为气动隐身一体化优化设计提供了优秀的平台，进而针对各类型作战飞机的气动隐身一体化研究成为国内外关注的热点[1-4]。

相比于常规布局的飞行器气动隐身优化设计，飞翼布局自身的结构特性使得其在隐身性能上优于常规布局飞行器。但也因此在缺失尾翼、垂尾等结构的情况下，其气动及结构载荷需要通过机翼来补足。国内外针对飞翼布局无人机做了大量研究。K.Hyoungjin等[5]针对一体化翼身融合体进行了详细地气动分析；王豪杰等[6]通过风洞实验对比，结合CFD完成对某型无尾飞翼布局无人机的气动力设计；在飞翼构型气动优化方面，王荣等[7]采用高精度粘性气动计算模型建立了飞翼布局无人机外形精度下的气动隐身多目标优化；张乐等[8]针对双发布局下的飞翼无人机大鼓包机身，提出了一种减小翼型前缘半径的机身前缘类“鹰嘴”形飞翼布局优化构型；陈曦等[9]开展了飞翼布局无人机在考虑隐身迎角下的气动隐身综合优化。

在针对飞翼布局无人机的多目标优化中，由于需要频繁调用目标函数，优化过程需要投入较大的时间成本和计算机资源。如何在平衡计算精度与计算效率的情况下建立一套高效的多目标优化算法，是目前亟待解决的问题。本文针对典型飞翼布局，结合基于EHVI(Expected Hyper-Volume Improvement)加点准则的高精度多目标优化算法，建立一种新的能够在较少调用目标函数的情况下完成优化任务的高效多目标粒子群优化算法，并对某型飞翼布局无人机进行隐身气动多目标优化设计研究。

1 高效多目标粒子群算法

1.1 多目标优化问题

在n维搜索空间S∈Rn内，定义一个目标数量为m的多目标优化向量fi(x),i=1,…,m，那么带约束的最小化多目标优化问题的通用数学模型可以表示为

minf(x)=[f1(x),f2(x),…,fm(x)]

(1)

s.t.gj(x)≤0,j=1,…,l

hk(x)=0,k=1,…,p

式中：x=[x1,x2,…,xn]，为设计变量向量；gj(x)为第j个不等式约束；hk(x)为第k个等式约束；l和p分别为不等式约束和等式约束的数量。

1.2 多目标粒子群优化算法

粒子群优化(Particle Swarm Optimization，简称PSO)算法最初是为了模拟鸟群的飞行觅食行为而提出的一种群智能算法。其初始化为一群随机粒子，通过迭代寻找最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己：第一个极值是粒子个体所找到的历史最优解，称为个体最优值Pb；另一个极值是整个种群目前找到的最优解，称为全局最优值Gb。在找到上述两个最优值时，粒子根据式(2)～式(3)来更新自己的速度和位置。

(2)

(3)

式中：c1和c2分别为认知和社会加速系数，取值范围为[0,4]，一般取c1=c2=2；r1和r2为两个在[0,1]内服从均匀分布的随机变量。

经过众多研究人员的深入研究，现在粒子群算法已可以方便地用于处理多目标优化问题。

CDMOPSO(Crowding Distance Multi-objective PSO)算法是C.R.Raquel等在C.A.C.Coello等提出的多目标粒子群算法(MOPSO)[10]的基础上，使用拥挤度算子代替超网格来维护外部档案而改进(如图1所示)的一种多目标优化算法[11]。拥挤度算子[12]能够通过选择引导粒子运动的最优解以及维护外部档案来增加种群的多样性，避免算法过早陷入局部最优。这种算法的优点是结构简单，易于实现，缺陷是基于均匀分布的变异操作使其易于陷入局部最优，解决多模态优化问题的能力较差。气动隐身多目标优化设计是一种高维强非线性问题，因此本文选择α-stable变异函数来对其进行改进，通过α-stable分布[13-14]产生的随机数，对PSO种群中的个体进行变异。在变异的过程中，通过动态调整函数的稳定系数α来调整不同优化阶段变异的范围和幅度。稳定系数α描述了分布的尾迹大小，决定了随机数的范围。α的变化范围是[1,2]。在开始阶段使用较小的α值，增强全局搜索能力，随着优化循环的进程，α值越来越大，全局搜索能力减弱，局部搜索能力增强，为寻找高精度解提供帮助。其具体变异操作过程以及优化结果对比详见文献[15]，流程图如图2所示。本文将其命名为ASMOPSO(Alpha-stable Multi-objective PSO)。

图1 拥挤距离计算示意图Fig.1 Schematic diagram of congestion distance calculation

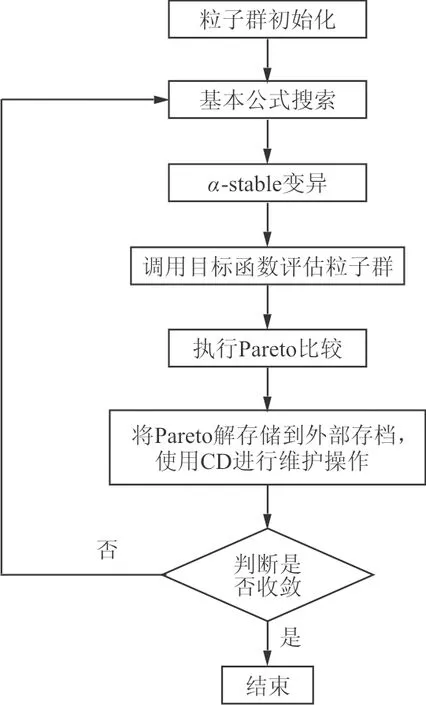
图2 ASMOPSO流程图Fig.2 Flow chart of ASMOPSO

1.3 基于Kriging模型的EHVI加点准则

为了增加局部地区的代理模型精度，减少对初始样本空间精度的依赖，采用基于自适应加点的动态Kriging代理模型对粒子群中的未观测点进行近似评估。在动态更新代理模型样本点的过程中，使用EHVI准则选择粒子群多目标优化过程中若干个最可靠的未观测点进行真实函数评估，更新Pareto解集，同时提高Kriging代理模型局部区域精度。

EHVI是M.Emmerich等[16-17]在超体积理论[18]的基础上结合单目标EI(Expected Improvement)加点准则[19]提出的一种处理高耗时优化问题的新型多目标加点准则。

给定一个新的解y，假设它不被Pareto解集P中的任意个体所支配，那么解集P的超体积改善为

H(y,P)=H(P∪{y})-H(P)

(4)

进而就可以定义超体积改善函数为

(5)

那么基于Kriging代理模型的多目标响应可视为互相独立且服从高斯分布的随机变量Yj(x)，有：

(6)

式中：m为目标数量。

在此基础上，可以得到多目标期望改善函数：

(7)

式中：Vnd为由Pareto解集确定的非支配区域，即如图3所示的细实线与坐标轴封闭的区域。

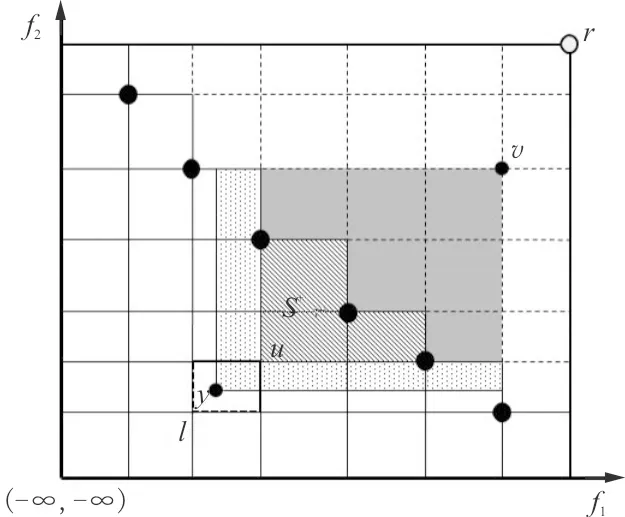
图3 超体积改善示意图Fig.3 Diagram of hypervolume improvement

从式(6)可以看出：如果要精确计算EHVI值，需要在非支配区域进行多维积分。由于非支配区域的不规则性，将超体积区域分割成多个矩形单元是必不可少的步骤。当Pareto解较多或者目标维度较高时，精确地识别这些矩形单元并对其进行EI积分是一件非常耗时的工作。

为此，Cheng Shixin等[20]提出了一种动态的EHVI值计算方式，通过对多个标准函数的对比测试结果分析，相比其基本型CDMOPSO优化算法，结合动态超体积期望改善的优化算法能在大幅度减少调用真实函数次数的情况下保持计算精度，极大地提高了优化效率。本文所使用的加点准则就是基于此动态计算方法的EHVI加点准则。

1.4 约束的处理

为了克服罚函数系数设定难的问题，优化算法中采用不可行度(Infeasibility Degree，简称IFD)法来处理优化问题中的约束[21]，当一个粒子处在不可行域内时，IFD值可以表示为粒子与可行域边界的接近程度，则定义第i个粒子的不可行度值为

(8)

式中：γ为等式约束的容限区间，γ≥0。

如果一个粒子位于可行域内，则它的IFD值为0，这种粒子称为可行粒子。基于不可行度和Pareto优胜比较的粒子选择机制是：①如果一个粒子可行，而另一个粒子不可行，那么选择可行粒子；②如果两个粒子都不可行，则选择IFD值较小的那个粒子；③如果两个粒子都可行，执行Pareto优胜比较，选择非支配粒子。

基于式(8)将每个粒子的近似不可行度改写为

(9)

1.5 基于EHVI的多目标粒子群算法

区别于传统的寻找当前Kriging代理模型下的最大EHVI值的子优化过程，本文计算当前种群中所有个体的EHVI值并对它们进行降序排列，选取前几个个体进行真实函数评估并加入样本集，用于更新外部非支配解档案，引导ASMOPSO中个体的移动。在这个过程中Kriging代理模型只是作为提供未观测点的均值和方差的工具，用于计算EHVI值，代理模型的精度不是首要考虑的因素。

综上，结合多目标粒子群算法、Kriging代理模型、EHVI加点形成的高效多目标优化算法(EHVIMOPSO)的流程如图4所示。

图4 EHVIMOPSO流程图Fig.4 Flow chart of EHVIMOPSO

2 气动隐身多目标优化设计

2.1 优化模型的建立

使用飞翼无人机作为初始外形，如图5所示，以翼面为研究对象，以阻力和RCS(Radar Cross Section)为优化目标，约束为升力系数不小于原始翼型和俯仰力矩系数绝对值不减小。设计点气动计算状态为：Ma=0.8,α=2.0°,Re=2.78×107。

图5 飞翼布局无人机几何外形Fig.5 Geometry of flywing UAV

由此可得优化的数学模型为

(10)

式中：X为设计变量向量；CD为阻力系数；ARCS为RCS均值；CL为升力系数；CM为力矩系数；上标*表示初始翼型的计算值。

2.2 计算网格及仿真计算方法

流体计算方面，流场求解基于三维非定常雷诺平均N-S方程，湍流模型采用k-ωSST模型，物面边界采用无滑移边界条件，远场采用压力远场边界条件。

本文使用半模计算，采用由ANSYS ICEM CFD软件生成的空间六面体网格对流动区域进行离散，网格数量为165万，计算网格如图6所示。在优化设计循环中，使用该软件自带的脚本功能实现网格的运动[21]。

电磁隐身特性求解以RCS为衡量标准，它描述了物体因被电磁波照射而向各个方向散射，被雷达捕捉的雷达回波强度及其电磁特性。在计算目标RCS的过程中，需要平衡计算效率与计算精度。由于不同的计算方法对于不同尺寸的目标具有不同的适应性，在选择计算方法时需要考虑目标的电尺寸大小。

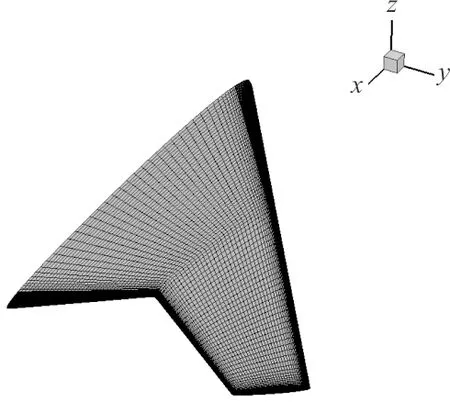
图6 计算网格Fig.6 Computational grid

综合考虑，本文选用大面元物理光学法LEPO(Large Element PO)配合一致性几何绕射理论 (UTD)计算边缘绕射场。计算状态为单站，极化方式为水平极化，雷达频率选择10 GHz。采用半模计算，计算范围(θ)为0°～180°，步长为1°。RCS计算示意图如图7所示。

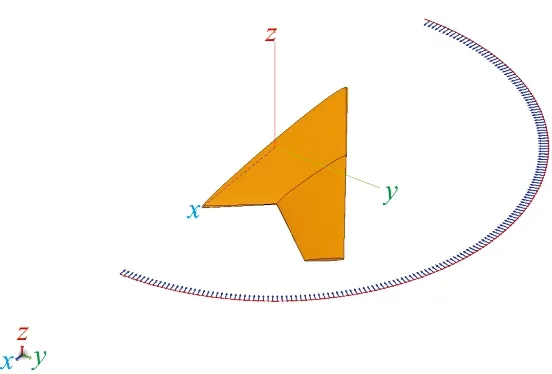
图7 RCS计算示意Fig.7 Diagram of RCS calculation

2.3 参数化方法

在优化设计中，采用空间变形能力较强的FFD(Free Form Deformation)自由曲面变形法[22]作为参数化方法。该方法最早由T.W.Sederberg和S.R.Parry提出，是一种针对三维可变形物体的有效建模工具。其基本方法是通过构建并操纵空间三维框架与被操纵面的映射关系，通过改变空间三维框架来改变被操纵面的形状。由于此方法能够适用于非常复杂的外形控制且模拟精度很高，在飞行器三维参数化中有较好的应用。

飞翼优化模型中的FFD参数化[23]空间控制点为翼面上下各25个控制点(如图8(a)所示)，在坐标系中，x、y、z三个方向上布置的控制点数为(5,5,2)，由于控制变量明显偏多，考虑在外形优化中将整个变形框外框固定不变，选择上下翼面中心位置的9个点(如图8(b)所示)，一共18个点，坐标系中表示在x、y、z方向上的点数为(3,3,2)，变形方向限定为仅在z方向上。为了不让变形过于剧烈，变形范围设定在±0.05之内。最后控制点一共为3×3×2=18个。

(b) FFD参数化翼面控制点示意图图8 翼面FFD参数化控制点Fig.8 Parameterized control point of airfoil FFD

在FFD参数化后，通过曲面差值生成新的飞翼翼面。参数化结果如表1所示，可以看出：FFD参数化后的代理模型与原始外形的翼面力学特性几乎完全吻合，隐身性能存在0.3%的误差，符合计算中的误差范围，故认为该参数化方法能够精确表达原始模型的气动外形。

表1 参数化结果比较Table 1 Comparison of parametric results

2.4 优化过程及优化结果分析

使用最优拉丁超立方抽样(Optimal Latin Hypercube Sampling，简称OLHS)[24]生成40个初始样本点，建立初始代理模型并通过EHVIMOPSO多目标优化算法搜索Pareto前沿。其中粒子群种群规模为200，外部档案大小为50；惯性系数从0.75逐渐减小到0.25；认知加速系数和社会加速系数c1=c2=2.0；稳定系数α的变化范围为1.0～2.0。迭代步数为60步，每代使用EHVI值选择3个最稳定的个体加入到样本空间中，并更新代理模型。优化结果如图9和表2所示。

图9 Pareto前沿Fig.9 Forward position of Pareto 表2 Pareto前沿数值统计Table 2 Frontier point of Pareto

序号CDARCS/m210.008 5151.065 95120.008 5471.053 66030.008 5221.061 07740.008 5251.059 75450.008 5361.053 8496(A点)0.008 5321.055 57170.008 5271.057 25880.008 5301.056 98090.008 5421.053 797100.008 5451.053 757

从图9和表2可以看出：Pareto解分布较为均匀，但是范围还不够宽广。

优化前后数据比较如表3所示。由于此飞翼布局无人机为低可探测低阻外形，其原始外形的气动及隐身性能非常优秀(如表1所示)，因此在此优化算法下的气动优化效果没有特别明显的提升。

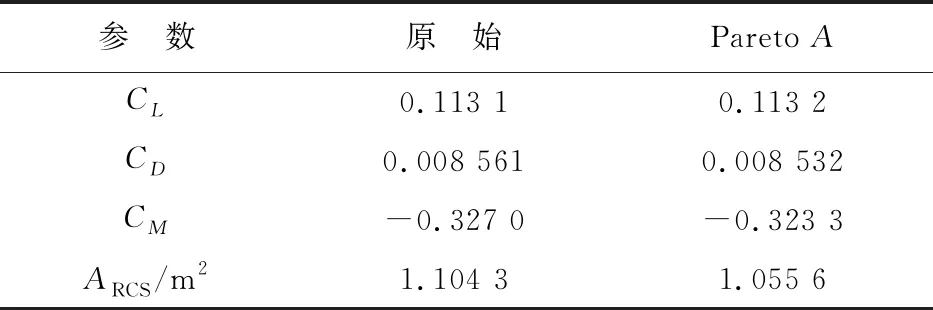
表3 优化前后数据比较Table 3 Data comparison before and after optimization

在平衡减阻与降低RCS两者情况下选择如图9所示的ParetoA与原始构型进行比较分析。

从表2可以看出：在ParetoA的构型下阻力减少了0.34%，RCS缩减了4.41%。

在气动计算结果对比方面，为了更好地说明，选取Y分别为1.0、2.5、4.5三个展向站位的翼型截面进行对比分析，如图10所示。优化后的翼型剖面形状、压力系数与原始外形对比结果如图11～图13所示。

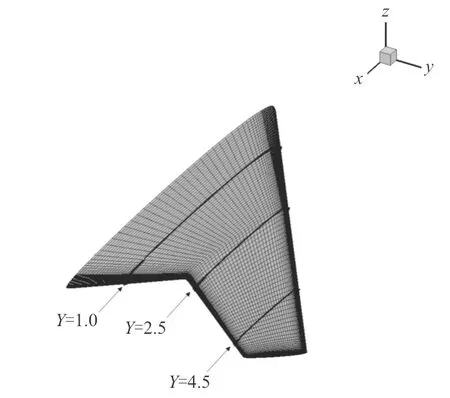
图10 翼面截取示意Fig.10 Sketch of wing interception

(a) 翼型对比

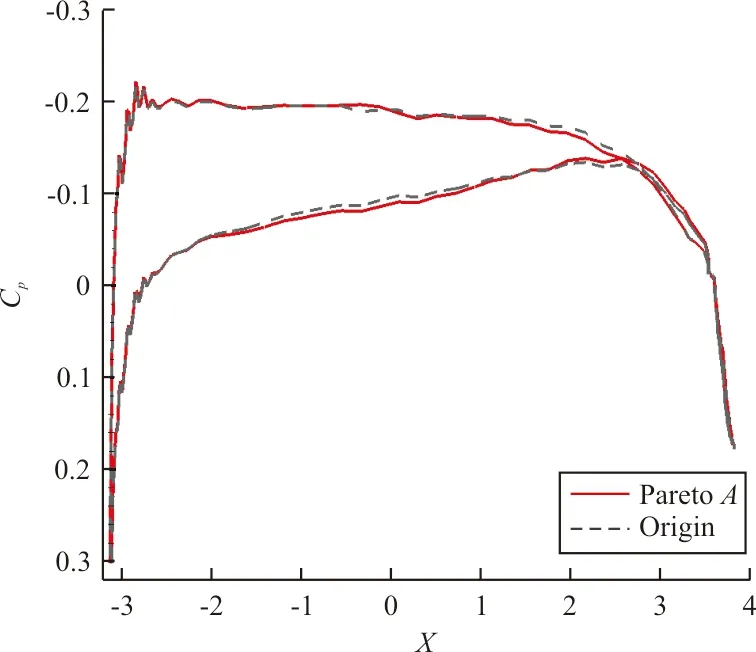
(b) 压力系数对比图11 对比结果(Y=1.0)Fig.11 Contrast result(Y=1.0)

(a) 翼型对比

(b) 压力系数对比图12 对比结果(Y=2.5)Fig.12 Contrast result(Y=2.5)

(a) 翼型对比

(b) 压力系数对比图13 对比结果(Y=4.5)Fig.13 Contrast result(Y=4.5)

从图11～图13可以看出：优化构型三个站位上的翼型剖面与原始翼型相比，在上翼面前部与下翼面后部都有小量缩减，翼面最大厚度向后移动且最大厚度值都减小、变薄，其中Y=2.5、Y=4.5两个站位翼型变薄的情况非常明显；翼型的前后缘位置压力分布较陡峭，中段压力系数曲线分布较为平缓，优化后构型仍能在此基础上有一定程度的减缓翼面激波强度；Y=1.0站位，后缘附近有一个向下的加载力区域，使的整个优化构型的低头力矩减小，提高了无人机的可操控性。

RCS优化结果对比如图14所示，可以看出：在入射角为57°和140°处有峰值存在，57°时的峰值为机翼前缘的电磁散射相干叠加而形成的，140°处的峰值为机翼端面造成的镜面反射；RCS缩减部位主要集中在60°～90°范围内，这是由于本文选择的翼面控制点在翼面中部位置，对于前缘和端面形成的电磁散射无法做到有效缩减。

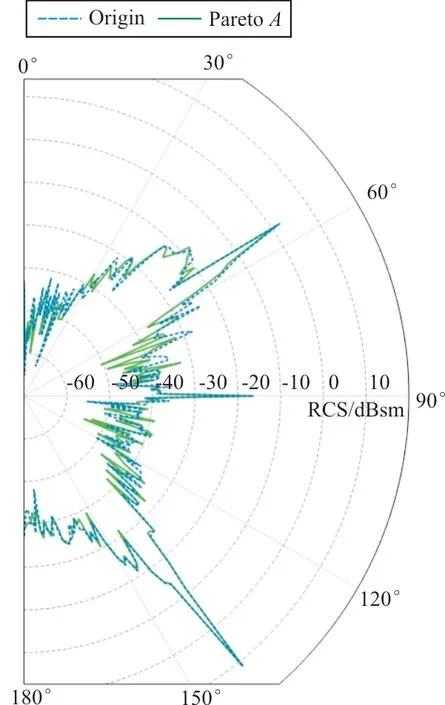
图14 优化结果A与原始外形的RCS计算结果对比Fig.14 Comparison of RCS calculation results between Pareto A and original profile

3 结 论

本文使用计算流体力学和计算电磁学等数值模拟手段计算飞翼布局无人机的气动和隐身性能，结合一种基于EHVI加点的高效多目标粒子群优化算法使用FFD法进行参数化表达，对一种低阻、低可探测飞翼布局无人机进行气动隐身多目标优化设计。在200次调用目标函数的情况下，降低了无人机的阻力和雷达反射截面积，表明本文提出的高效优化设计方法在解决类似飞翼式布局无人机气动隐身多目标优化设计等昂贵优化问题时具有较大的应用潜力。