主题聚焦渐次展开微型专题精准备考

刘东升 王俊蓉

最近一次跨地区（江阴市与海安市）初中数学教研活动上，我们把研讨主题确定为中考微专题，让专题复习的主题更加聚焦。由于承办地安排在江阴，为了贴近无锡地区中考风格，我们共同打磨研发了一节关注综合题中“直线表达式”的求解专题复习课。本文先简要整理该课的教学设计，再给出教学立意的相关阐释，以供分享和研讨。

一、综合题中“直线表达式”的求解专题复习课

活动1 自主先练，开课交流。

问题1 已知，平面直角坐标系xOy中，直线y=kx+b经过A，B两点。

（1）若点A（6，0），B（0，4），求k，b的值;

（2）若点A（[133]，0），B（0，[132]），求k，b的值;

（3）若点A（0，0），B（[72]，[32]），求k，b的值;

（4）若点A（3[5]，5），B（0，-1），求k，b的值。

教学组织：这组练习可安排学生课前完成，开课之后就进行板演或投影，引导学生互评解答。

设计意图：已知两点坐标求解直线表达式，考查的是基本运算能力。课前安排学生先练，节约了课堂复习时间，并且这4个运算求得的结果，分别对应着本课后续一些综合题中的解答，能让学生在后续复习活动中把更多的精力用在思路分析与解法优化上。

活动2 旋转变换后求正比例函数的表达式。

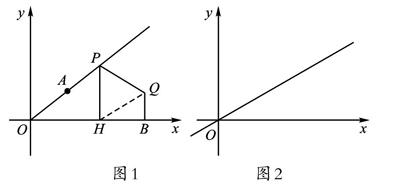
问题2 已知，平面直角坐标系xOy中，点A（2，[3]）。在射线OA上任取一点P（m，n），其中m，n为正实数，过点P作PH⊥x轴，垂足为H。

（1）直接写出直线OA的表达式，并用含m的式子表示n。

（2）将PH绕点P逆时针旋转60°到PQ的位置，点H与点Q为旋转前后的对应点。求直线OQ对应的函数表达式。

教学组织：安排学生先根据题意构造草图分析，并先解决第（1）问，处理第（2）问时分析Q点的坐标。学生可能会构造图1进行分析。可安排学生上台讲解思路。在此基础上跟进一道变式习题。

图1                        图2

变式：如图2，平面直角坐标系xOy中，将直线y=[12]x绕原点逆时针旋转45°后所得直线对应的函数表达式是__________。

教学组织：安排学生先画图分析，解题的关键是分析出旋转后直线上某个特殊点的坐标，然后就可确定直线表达式。

设计意图：这个活动及变式的立意主要是让学生感受在平面直角坐标系中分析旋转变换后某点的坐标，是确定过这点与原点的直线表达式的关键。

活动3 求综合题中直线对应的函数表达式

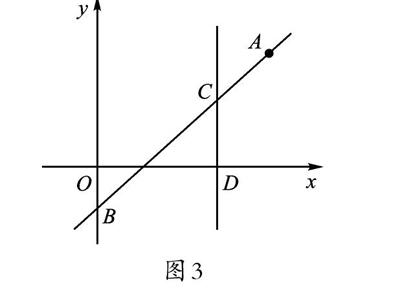
问题3 已知，如图3，一次函数y=kx-1的图像经过点A（[35]，m）（m>0），与y轴交于点B，点C在线段AB上，且BC=2AC，过点C作x轴的垂线，垂足为点D。

（1）当CD=2时，求直线AB对应的函数表达式;

（2）小江设计一个问题：若AC=CD，求直线AB与x轴交点的坐标。你觉得“小江问题”该如何解决？请思考后先在小组内交流大致思路或解题方向，再演算求解。

图3

教学组织：（PPT渐次呈现）教师提问，“你能读出哪些信息？”学生在小组内交流分享个人理解，然后PPT再渐次呈现后续两个小问。在学生独立思考演算解答之后，再安排学生上台讲解。

设计意图：这个题组改编自无锡地区中考综合题，将其中关键步骤分解、重组成这一问题串，以帮助学生训练中考较难题中的关键一步。

活动4 求“位置不定”的直线对应的函数表达式

平面直角坐標系xOy中，已知原点O、点A（a，0）、B（0，b）、C（6，4）四点在同一个圆上，其中a，b为正实数。

教学组织：先PPT呈现，请设计一个问题并求解，然后小组内交流。

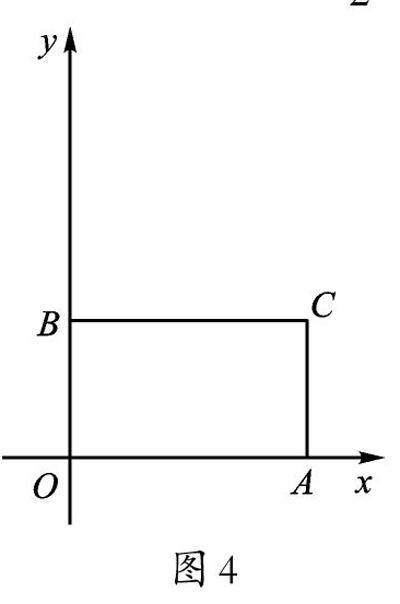
教学预设：∠ACB=90°;求tan∠ABC的值为[23];再比如增设“如图4，当四边形AOBC是矩形时”，还可继续引导学生探究它的外接圆的直径是[213]，半径是[13]等。目的是为了引出较难的一道挑战题。

挑战：连接AB，AC，BC，当△ABC与△AOB的面积相等时，求直线AB对应的函数表达式。

教学预设：学生可能会容易想到四边形AOBC是矩形的情况（如图4），这时可求出直线AB对应的函数表达式为y=-[23]x+4;另一种情况（如图5）是作线段OC的垂直平分线，与x，y轴的交点就是符合要求的点A，B。此时直线AB对应的函数表达式是y=-[32]x+[132]。

                  图4                           图5

课堂小结：

1.在综合题中涉及求直线对应的一次函数表达式，你觉得有哪些经验值得分享？小组内分享，可以结合本课中提到的一些题例分享各自的经验。

2.这节课主要复习综合题中涉及一次函数表达式的求解;无锡考卷中的一些中考真题有哪些呢？布置三道作业，2017年无锡中考试卷第25题，2018年的第26题、第28题。

二、教学立意的进一步阐释

第一，专题突破，让复习主题更加聚焦。

就我们在学校听课所见，多数中考专题复习课仍然沿袭着“开放题”“规律探究题”“阅读理解问题”“运动变化问题”等专题分类方式。以上述专题分类，只是从试题的“外形”上进行划分，似乎有一定的道理，但从具体来看，这些“形似”的专题放在一起，很可能它们涉及的知识点、解题策略却是“各不相同”的。这样的专题复习课难免会“七零八碎”，复习效益难有提升。我们提出中考微专题的复习追求，比如上文课例中主题关注综合题中的直线表达式的求解，就是从“形似”走向“神似”，将那些解题策略相近、涉及知识点相近的习题聚集在一起，串珠成线，提炼主线，让复习主题更加聚焦，追求专题复习效益的显著提升。

第二，贴近中考，让复习选题更加精准。

从上文课例中的选题可以看出，我們在不同“活动”下预设的系列问题都改编自无锡地区的中考真题，这也是最后布置作业时提到这些考题的原因。目前江苏的中考都是各大市独立命题，每个地区中考试卷都有明显的地区风格或“考查喜好”。我们研究了近三年无锡中考最后三道综合题，在这些题中都涉及确定直线表达式的考查要求，这也是我们研发这节微专题的主要用意。中考备考，时间紧、任务重，如何精准备考、高效备考，我们认为贴近地区中考命题风格的选题复习才是精准有效的。那种盲目选取外地“无关”考题的所谓链接中考是要不得的，浪费学生宝贵的复习时间，得不偿失。

第三，预设铺垫，让较难问题渐次展开。

由于本课选题的来源是近几年无锡中考综合题，虽然进行了改编、删减，聚焦了综合题中直线表达式的确定，但是课堂教学时间还是偏紧，如果只是呈现“原生态”的考题，学生就更难在一节课中突破几个较难问题。所以，我们在课前就针对这些较难题预设了铺垫式问题，比如“活动1”就是后续三个活动的铺垫，让学生课前先把一些基本运算都解决掉;再比如“活动3”中综合题本来要分类讨论，但我们通过开放式设问、跟进追问，在较难题呈现前已有了必要的铺垫，比较优秀的学生就能循着前面的问题，较顺利地获得思路和解答，既节约了课堂教学时间，也给了学生求解较难题的思路启示，这是通过“学习解题”达到帮助学生“学会解题”的一种追求。

（作者单位：①江苏省海安市城南实验中学;②江苏省江阴市教师发展中心）

【参考文献】

[1]刘东升.中考专题复习课：求联求变让老歌新唱——以中考“二次三项式再认识”复习为例[J].中学数学，2019（2）：54-55，60.

[2]刘东升. “形散神聚”的主题，“浅入深出”的环节——中考二轮微专题复习课“无处不在的边角关系”教学流程与立意[J].教育研究与评论（中学教育教学），2018（04）：87-91.

[3]刘东升.“开放”需要“放开”，“对话”促进“生成”———“二次函数复习”展评课的设计、对话与思考[J].中学数学月刊，2012（11）：26-31.