特殊大气环境下格尼襟翼的气动特性

崔 钊, 谢 强, 张 华, 韩 东, 李建波

(1.中国飞行试验研究院 飞机所, 陕西 西安 710089; 2.南京航空航天大学 航空学院, 江苏 南京 210016)

0 引 言

临近空间通常指距地面20～100 km的空域，高度介于航天空间和航空空间之间。军事需求牵引和技术发展推动，使临近空间成为了当今航空航天发达国家的研究热点[1]。相比轨道卫星或常规航空飞行器，部署在该空域的临近空间飞行器具有优于卫星的对地观测分辨率和电子对抗效果，在通信中继距离和侦察视场范围等方面则优于飞机，因此具有独特的优势。作为一种新型平台，临近空间飞行器[2-3]不仅是卫星和飞机的补充，更代表了一个新技术领域的广阔前景。目前各航空大国先后在临近空间飞行器领域投入了大量的科研力量。

虽然临近空间飞行器的应用前景十分广阔，但临近空间大气稀薄、大气压强很低、辐射水平高、低温并存在持续的风场，这些特有的环境因素增大了研制的技术难度。仅就空气动力学特性而言，临近空间飞行器也面临着与常规飞行器截然不同的气动环境。临近空间大气密度很低，要保持足够的升力需要足够大的翼面积和飞行速度；而临近空间的声速却低于海平面，因此临近空间飞行器往往处于雷诺数很低、马赫数却较大的气动环境中。尤其是升力型低动态临近空间飞行器，首先面临低雷诺数和高马赫数的特殊气动问题。

与临近空间飞行器气动问题类似的还有火星探测飞行器[4-7]。火星探测飞行器是一种专用于火星表面探测的近地飞行器。火星表面地形复杂，地表凹凸不平且布满沙坑和碎石，严重影响了火星探测车的行进和展开，“机遇号”和“勇气号”火星车都曾为沙坑所陷。而且火星车的探测范围有限、速度缓慢、机动能力差，因此在可预见的未来，探测平台的能力将会成为制约火星探测技术进一步发展的重要因素。然而火星表面存在以二氧化碳为主要成分的稀薄大气层，这为飞行器在火星的使用提供了基本条件，同样为火星探测平台的进化提供了一个契机：火星飞行器能够提供比火星车更大的探测范围，比轨道卫星更高的探测精度，是现有火星探测平台的一个重要补充。

但无论在临近空间还是在火星表面，升力面都面临着极低的大气密度，如何产生足够的升力是一个最为关键的问题。通常可以通过增加飞行速度、增大翼面积或提高翼型升力系数来增大翼面升力。在低密度条件下由于声速较低，马赫数会显著增大，阻力随之快速增加。而增大翼面积会使结构重量增大，升力产生的成本较高。本文提出通过格尼襟翼(Gurney flap，简称GF)来增大翼型升力系数，达到升力面性能提升的目的。

格尼襟翼是一种典型的后缘微型流动控制装置，已有的研究表明格尼襟翼增升效果显著。20世纪70年代Liebeck[8]率先开展了格尼襟翼气动特性的研究，通过Newman翼型风洞试验证实了格尼襟翼的增升减阻作用，更重要的是他首次提出了格尼襟翼后缘流动结构假设，即格尼襟翼使尾流向襟翼方向偏转，并在襟翼背风面形成了独特的双涡涡系结构，从而改变了翼型的后缘库塔条件和环量。Neuhart和Pendergraft[9]在水洞中观察到了格尼襟翼后的涡系结构，证实了翼型尾流的偏转。Jang等[10]采用数值计算的方法开展了格尼襟翼气动特性研究，表明格尼襟翼增大了翼面气动载荷，并会影响翼型气流分离的位置。Storms[11]研究了格尼襟翼和涡发生器对NACA4412翼型气动特性的影响，表明格尼襟翼显著增大了翼型升力系数和低头力矩系数，在高升力系数下能够减小阻力。Storms和Ross[12-13]通过风洞试验和数值模拟研究了NACA 两段翼型加装格尼襟翼的气动特性，表明主翼后缘附近加装格尼襟翼，在襟翼偏角较大时能够显著增升；在襟翼后缘安装格尼襟翼，则能够在任何襟翼偏角下增大升力系数。他们认为格尼襟翼使流经襟翼的气流偏转加剧，减小或消除襟翼上的气流分离，这是多段翼增升的主要原因。Myose等[14-15]针对格尼襟翼采用NACA0011翼型开展了低速风洞试验，研究表明加装格尼襟翼后升力系数线性段斜率基本保持不变，零升迎角减小，由此认为格尼襟翼实际上增大了翼型的有效弯度。Papadakis[16-17]、Jeffrey[18-19]、李亚臣和王晋军等[20-22]，对格尼襟翼的气动特性、流动机理和增升机制相继开展了一系列的研究，此外李亚臣和王晋军等还开展了格尼襟翼跨声速[23-24]和低雷诺数[25]特性的相关研究。

大量的研究已表明了格尼襟翼显著的增升效果，同时该增升装置结构简单、附加重量很小、无需特殊维护，便于在临近空间或火星大气条件下使用。本文针对在低雷诺数、跨声速的特殊使用条件下，翼型加装格尼襟翼的气动特性开展研究。基于数值计算方法对不同雷诺数和马赫数下，翼型加装不同高度格尼襟翼的气动系数、压力分布和流场特征进行了对比，为临近空间或火星飞行器的增升减阻设计提供技术支持。

1 数值计算方法

以二维可压N-S方程作为控制方程，采用有限体积法进行离散。空间离散采用通量差分分裂格式Roe-FDS (Flux Difference Splitting)，该格式计算跨声速可压流时具有较高的模拟精度。采用耦合隐式算法联立求解动量方程、能量方程和湍流黏度。控制方程由S-A (Spalart-Allmaras)湍流模型进行封闭，湍流模型给出湍流黏性系数，Sutherland定律计算层流黏性。虽然转捩模型能够更好地模拟低雷诺数层流分离泡，但S-A模型仍然能够正确反映低雷诺数翼型气动力的变化趋势。另外采用多方程转捩模型，计算耗费的资源要远大于S-A模型。而本文主要计算格尼襟翼对翼型特性的相对影响，因此采用S-A湍流模型。

采用理想气体模型，外边界半径约为25倍翼型弦长，边界条件为远场压力，指定远场来流的马赫数。翼型壁面为无滑移、无穿透边界。计算状态下雷诺数为0.5×105～2.0×105，马赫数为0.5～0.8，襟翼高度分别为弦长的0.5%、1.0%和2.0%。计算网格如图1、图2所示。

图1 C-H型流场网格

2 算例验证

由于临近空间和火星飞行器的相关研究尚处于起步阶段，目前还鲜见类似条件下的试验开展，因此缺少可用的公开试验数据作为算例验证。以文献[26]中ADPAC(Advanced Ducted Propfan Analysis Code)代码的计算结果作为本文计算方法的验证数据。

文献中采用ADPAC数值分析代码计算了Eppler387翼型在低雷诺数、跨声速下的气动系数。图3和4分别为翼型在雷诺数为1.0×105、马赫数为0.55和0.65时翼型的升力系数和阻力系数曲线。在中小迎角下，本文计算的翼型升力系数与ADPAC代码的计算结果基本一致，大迎角时最大升力系数和失速迎角低于ADPAC的结果。在全迎角范围内二者的阻力系数计算结果基本吻合。目前翼型数值计算通常能够较好地模拟翼型表面压力分布，难点在于阻力系数的精确计算。与国外计算结果的对比表明，本文计算方法可用于低雷诺数、高马赫数条件下翼型气动特性的分析。

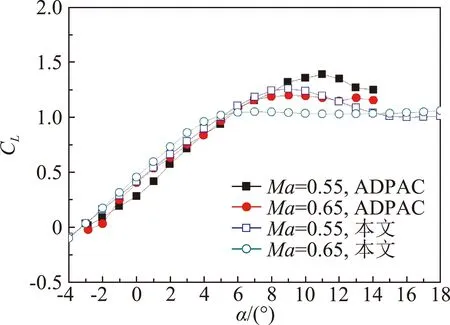
图3 Eppler387翼型的升力系数验证

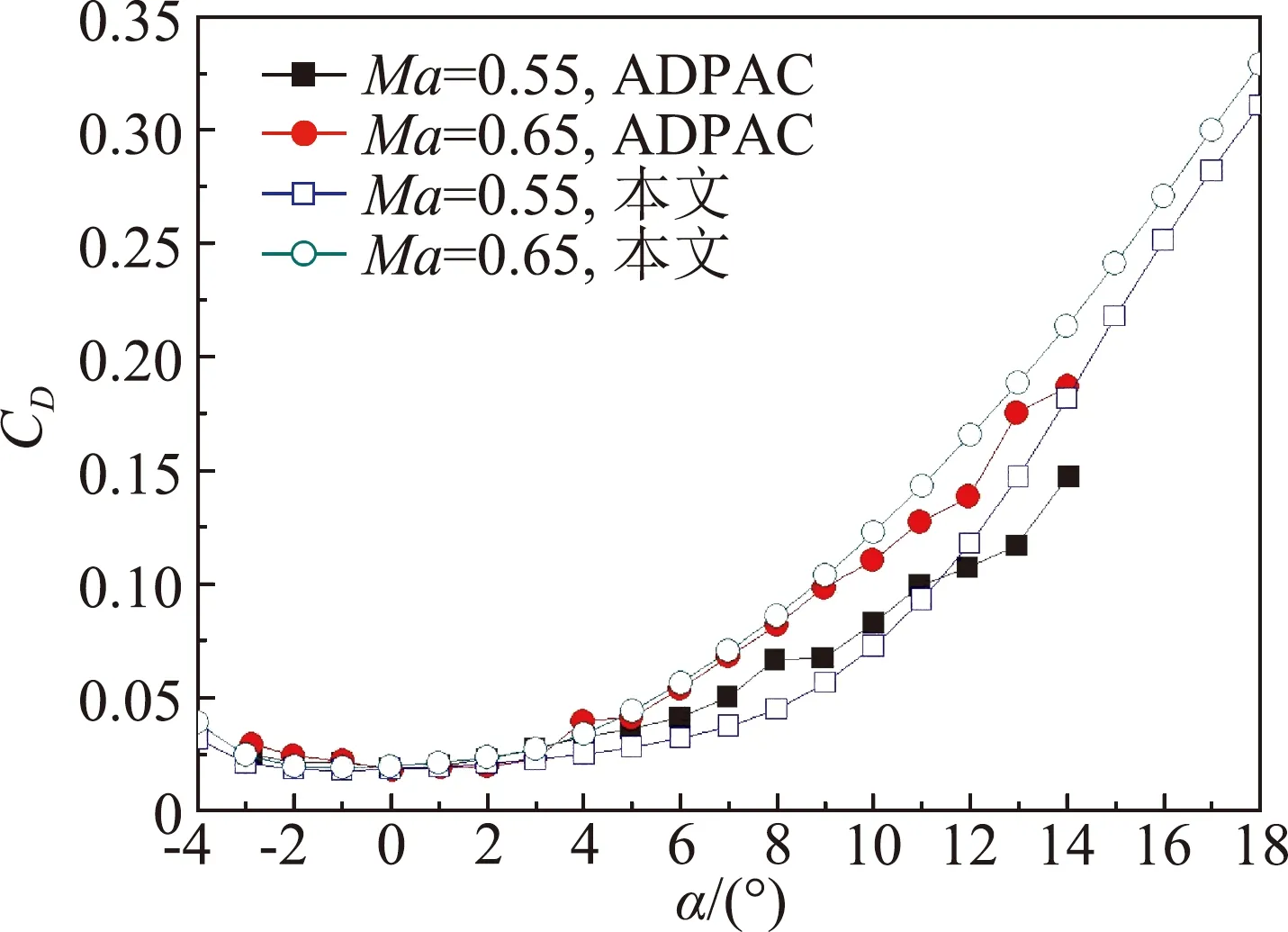
图4 Eppler387翼型的阻力系数验证

3 计算结果与分析

图5为雷诺数1.0×105、马赫数0.6下翼型加装格尼襟翼的表面压力分布。此时翼型表面激波较弱，加装襟翼后翼型上下表面压差增强，这表明格尼襟翼增大了翼型的环量。随襟翼高度增大翼型环量增大。在4°迎角时格尼襟翼显著增大了翼型的前缘吸力，形成了局部吸力峰。

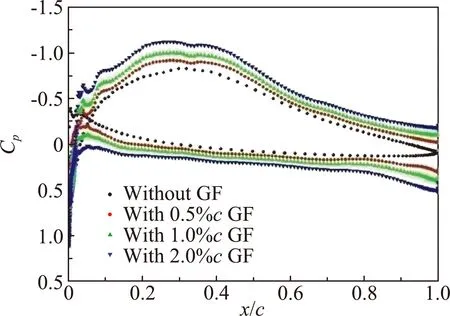
(a)α =0°

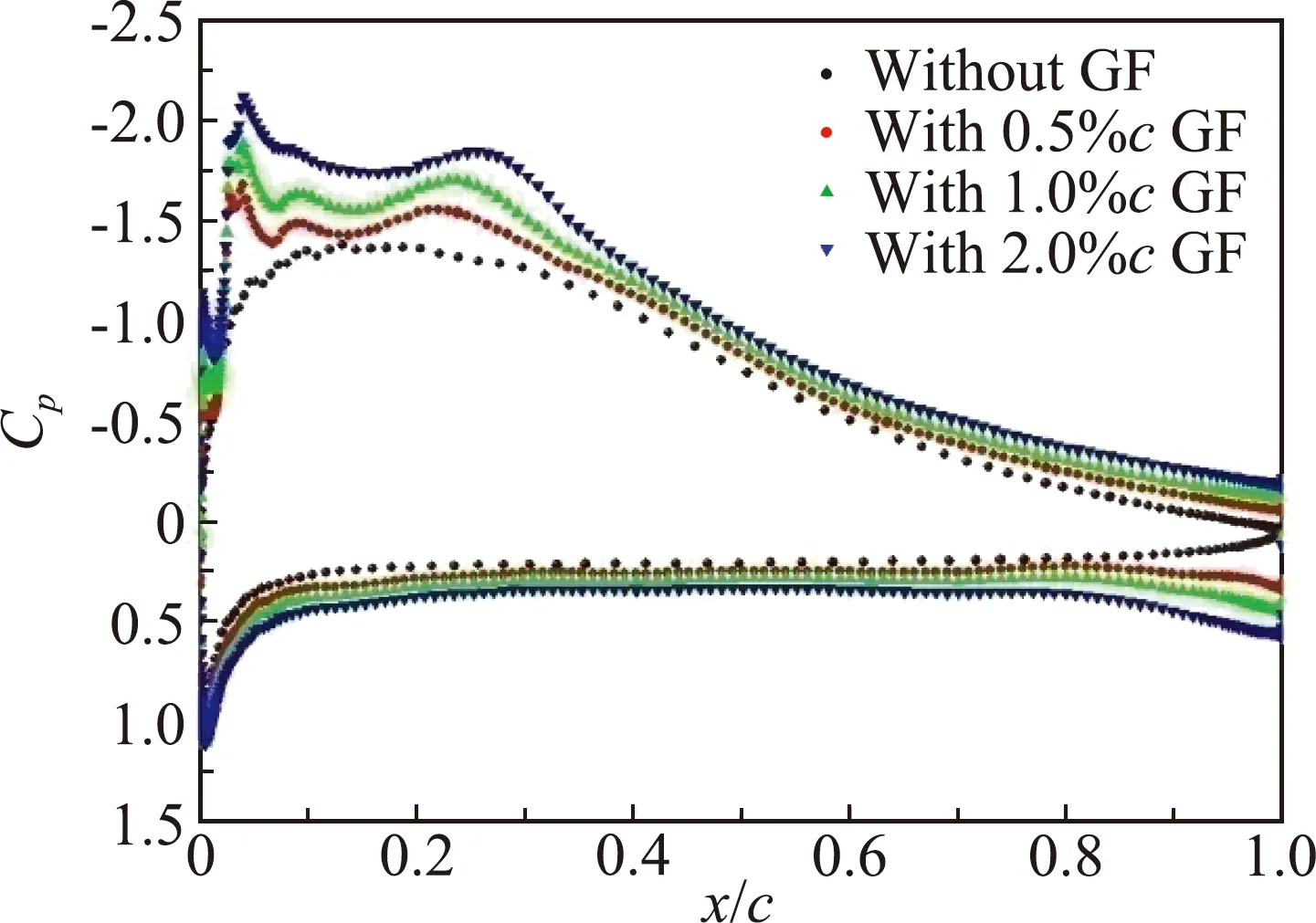
(b)α =4°

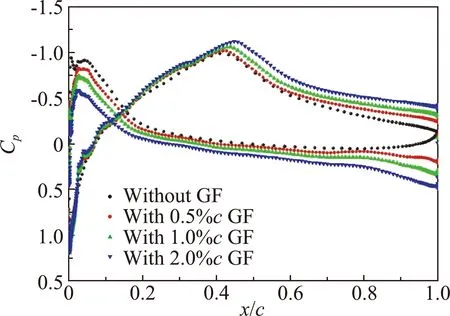
图6为马赫数0.8时翼型加装格尼襟翼的表面压力分布，格尼襟翼同样增大了翼型环量。马赫数0.8时翼型形成了明显的激波，图6(a)中在0°迎角时，加装格尼襟翼后，翼型上表面激波位置向后缘推迟，襟翼高度越大激波位置越靠后。图6(b)中在4°迎角时，0.5%c和1%c格尼襟翼对翼型上表面压力分布的影响很小，但增大了下表面压力，2%c格尼襟翼能够推迟翼型上表面激波，同时增大激波后的负压。图7为马赫数0.8时的翼型压力分布云图。可以明显看到1%c格尼襟翼增大了翼型上表面的低压区范围，同时削弱了前缘下表面的低压区域，由此翼型的升力增大。

(a)α =0°

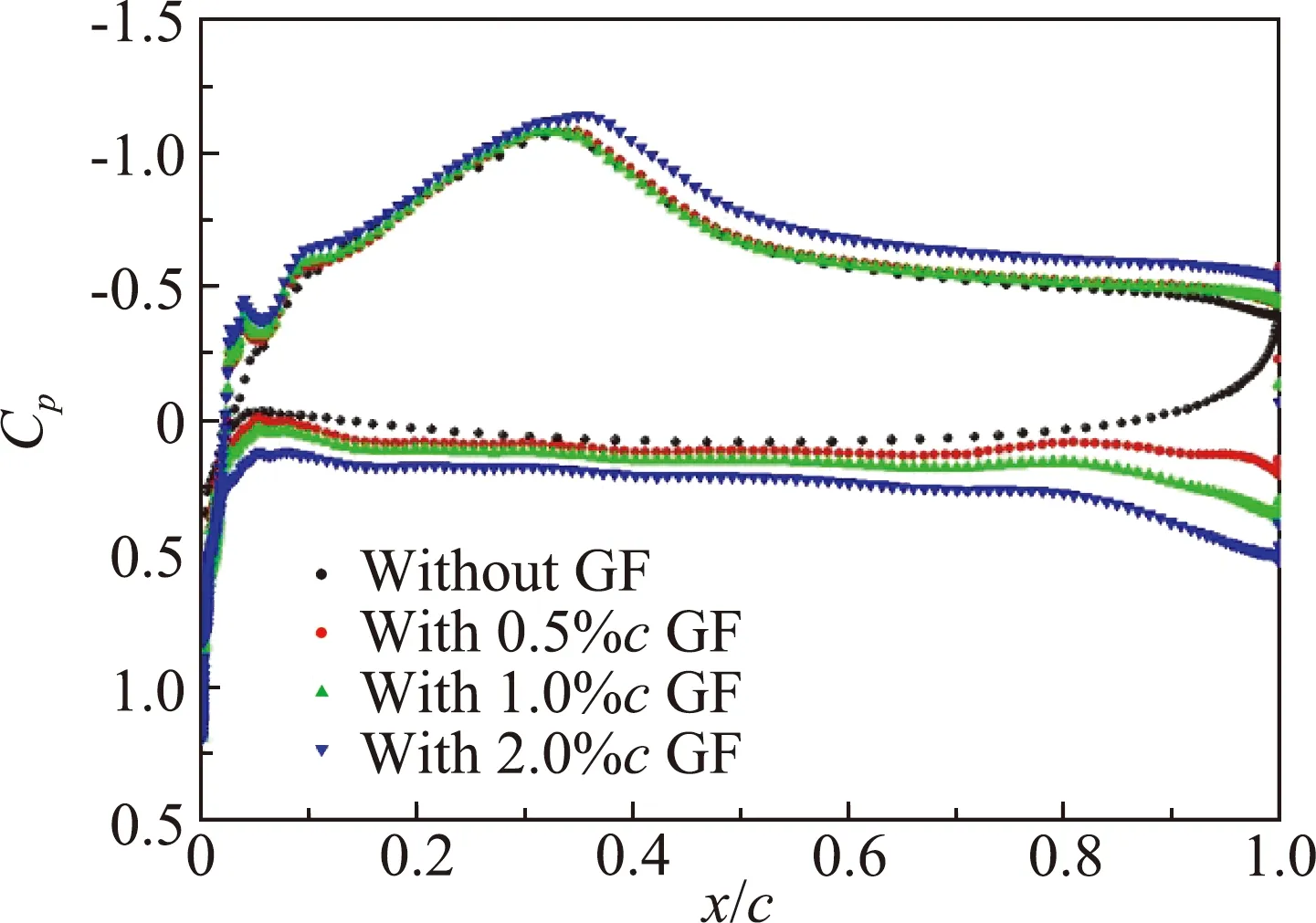
(b)α =4°

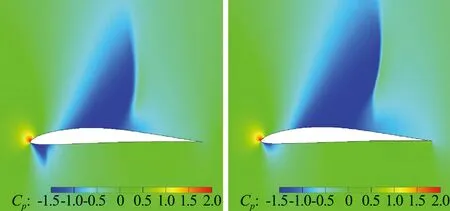
(a)Eppler387 (b)1%c GF

图8和9为马赫数0.8时，原翼型和加装格尼襟翼后翼型的速度流线云图。相比原翼型，1%c格尼襟翼使翼型上表面气流速度增大。这是由于加装襟翼后，后缘分离涡覆盖的范围明显扩大，加剧了上表面绕流在后缘附近的弯曲和偏折，从而起到了引流的作用。

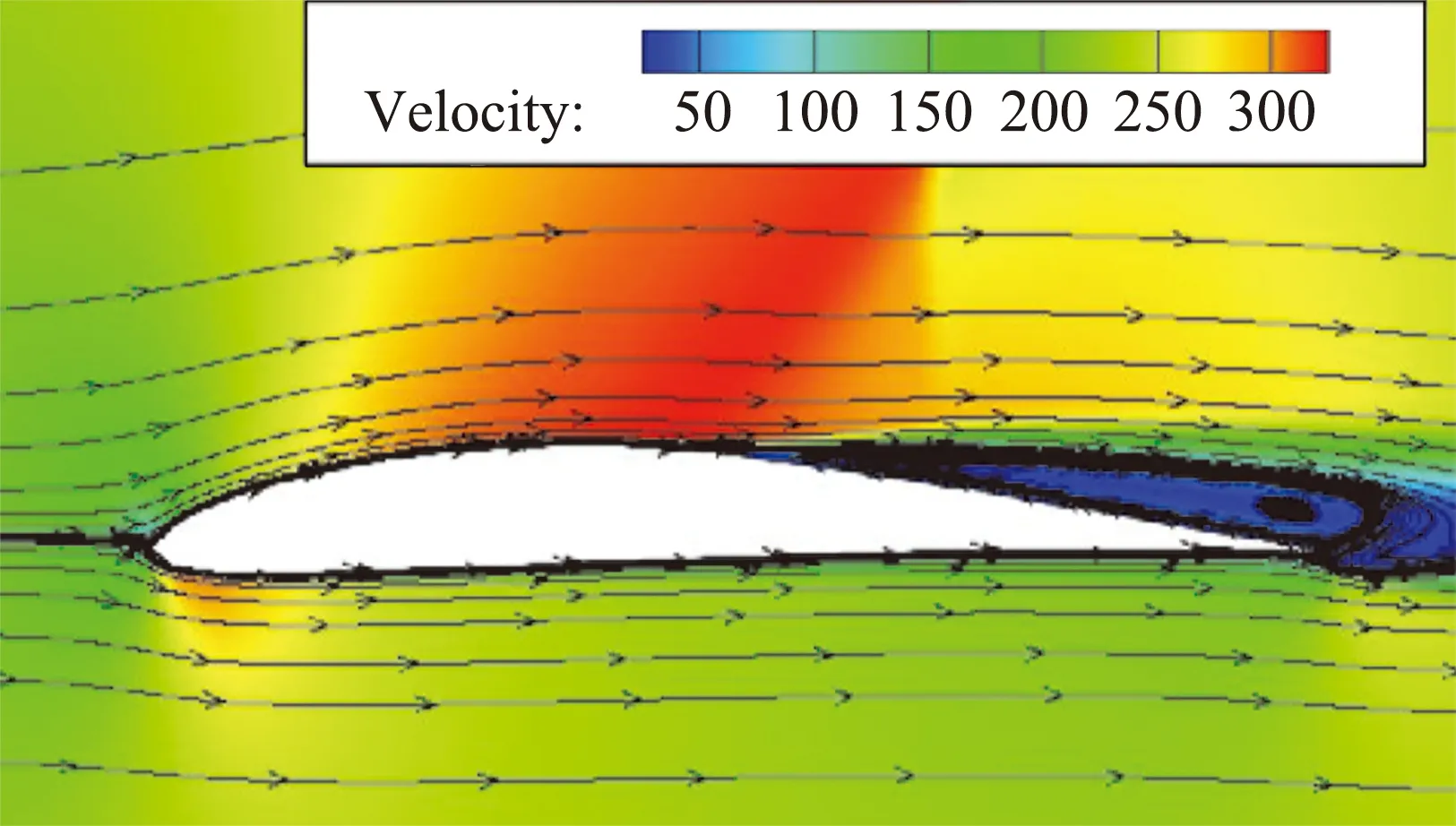
(b)1%c GF

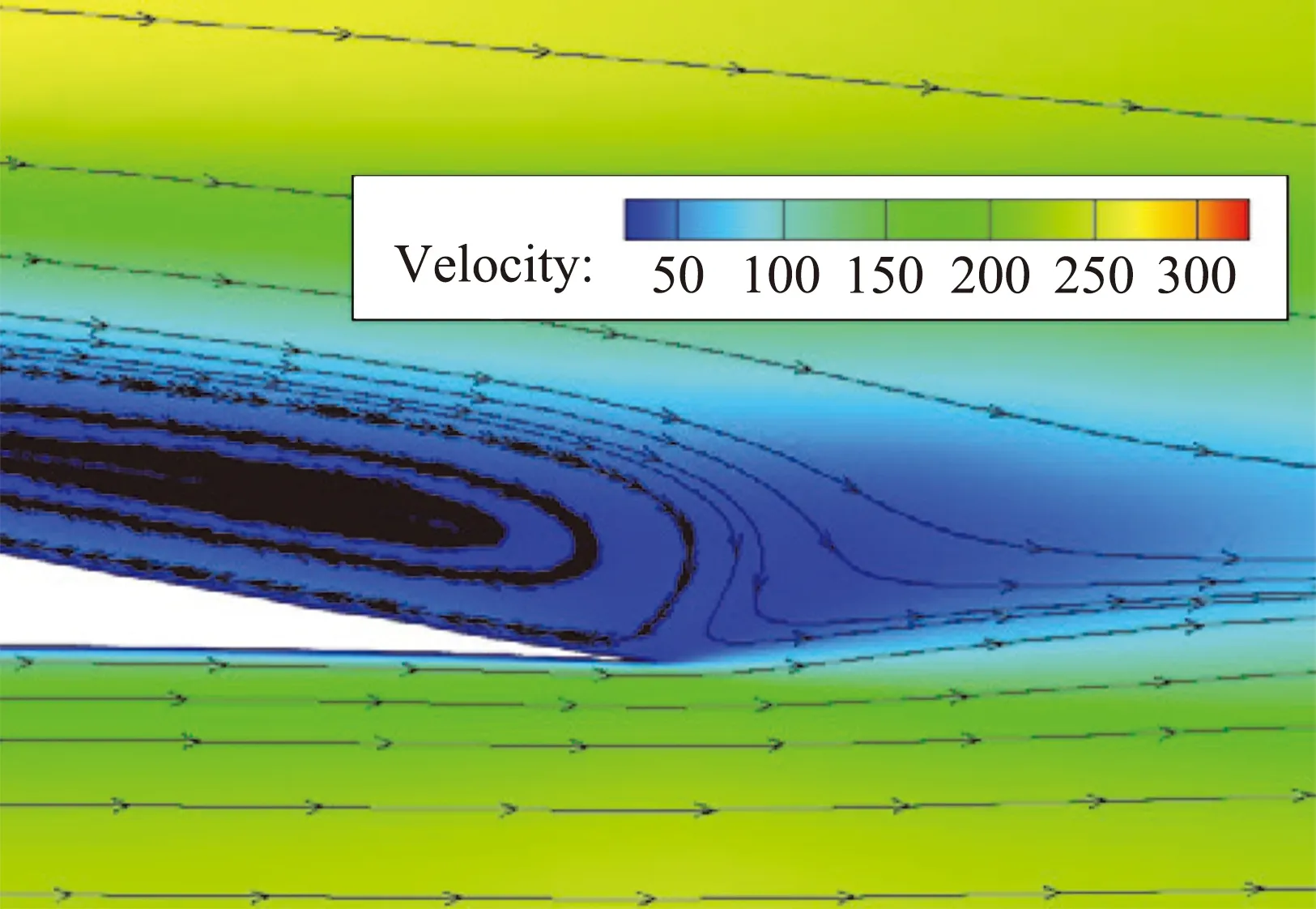
(a)Eppler387

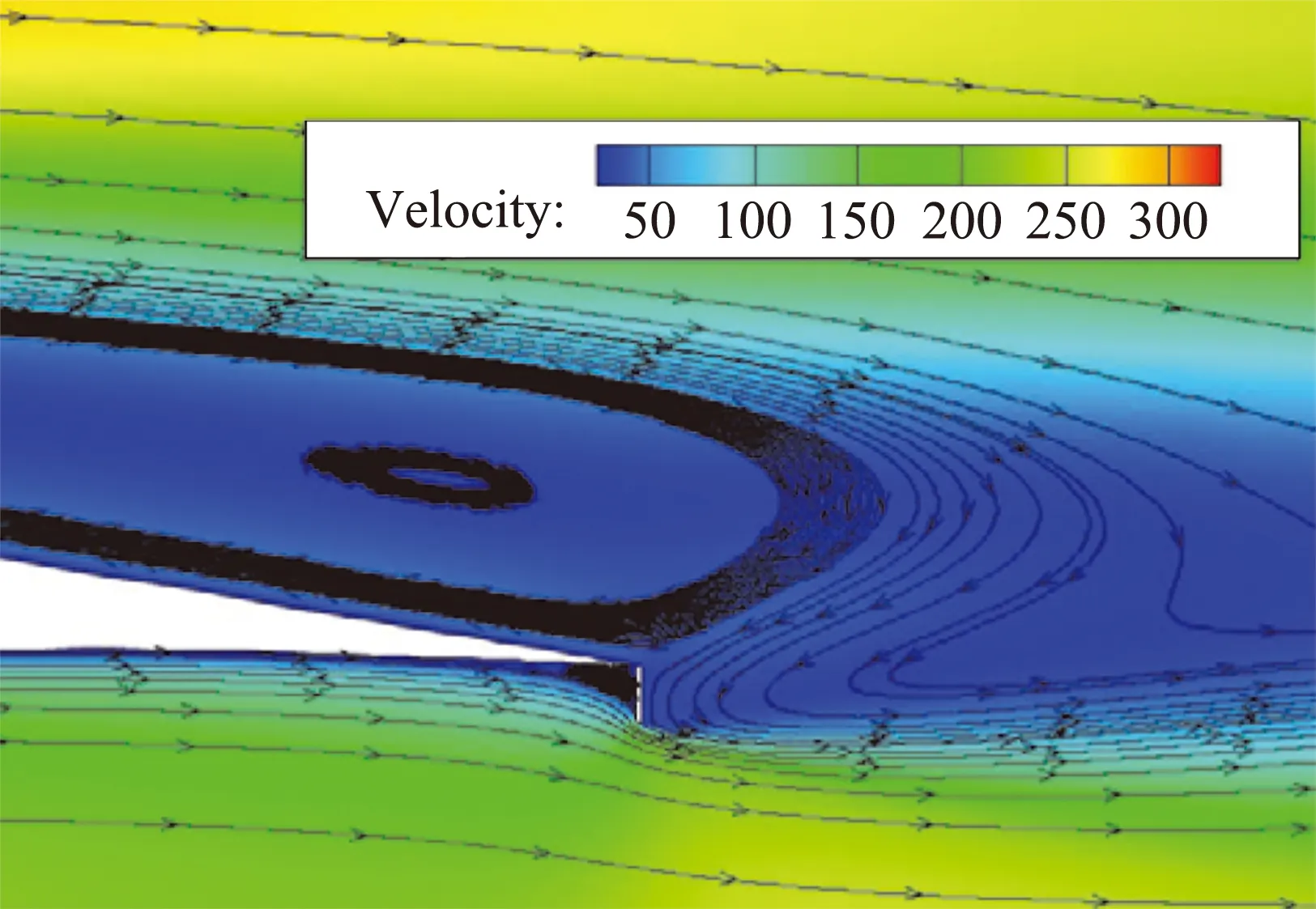
(b)1%c GF

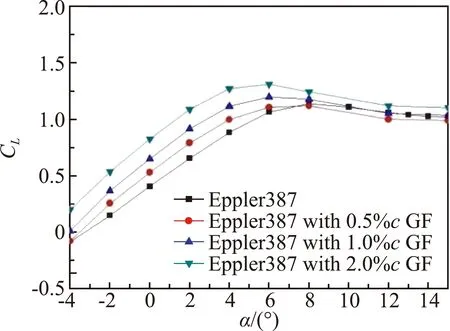
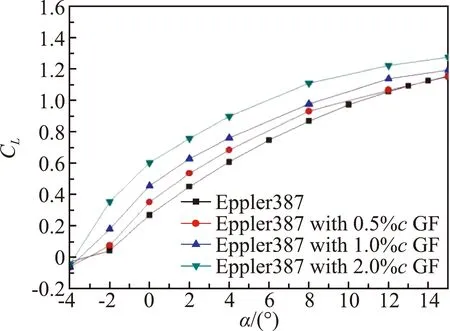
图10～图13为翼型升力系数和升阻比曲线。在低雷诺数、跨声速条件下，加装格尼襟翼后，翼型升力系数明显增大，随襟翼高度增加升力系数增加。图10(a)中加装格尼襟翼后，翼型的失速迎角减小，0.5%c和1%c襟翼的失速迎角由8°减小到6°，而2%c格尼襟翼的最大升力系数位于4°迎角附近。在失速后，格尼襟翼的增升幅度有所减小。而在马赫数0.8时，从升力系数曲线上看,翼型失速特性不再明显，在-2°～8°迎角内保持了较大的增升幅度。

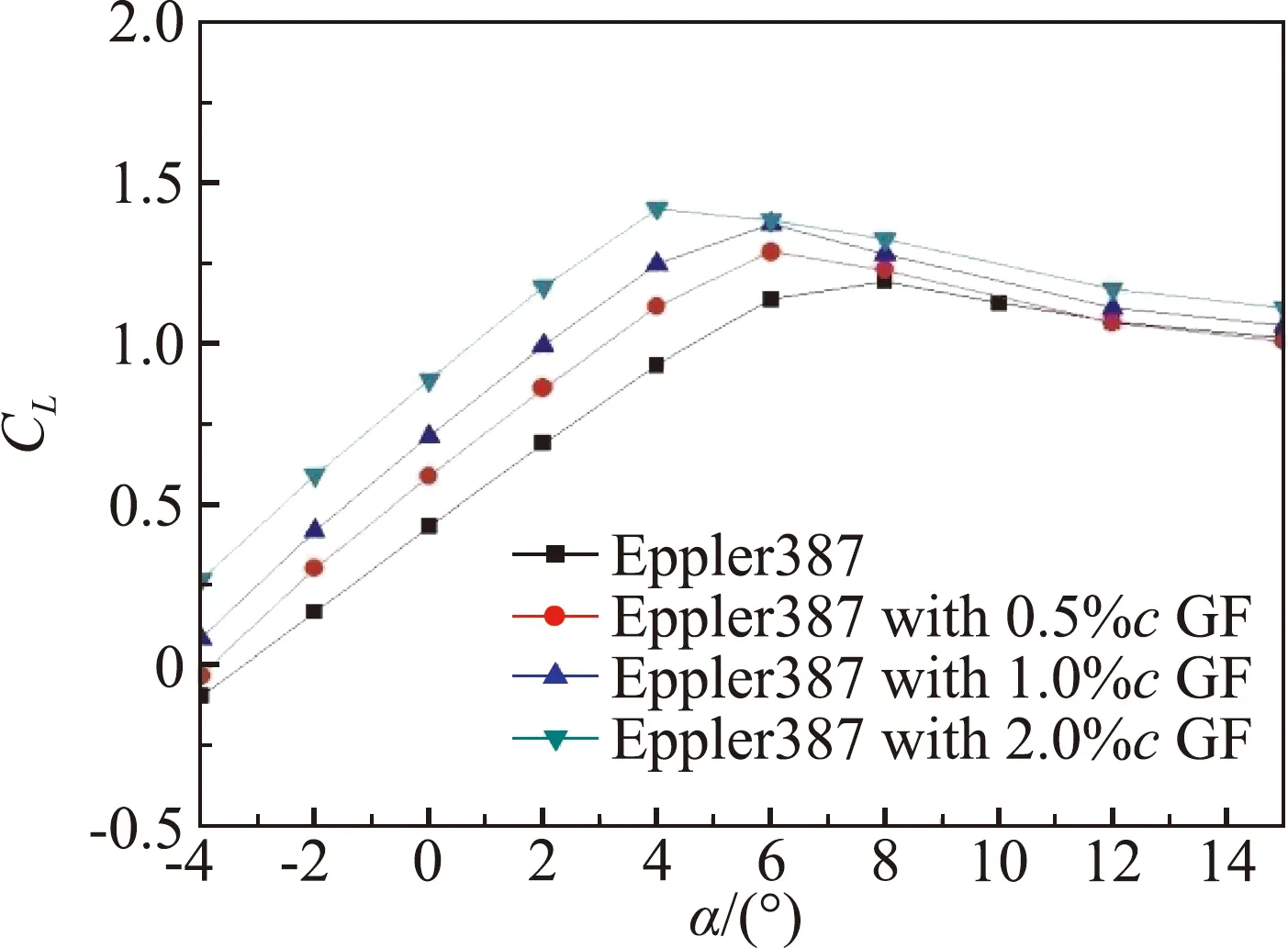
(a)Ma=0.6

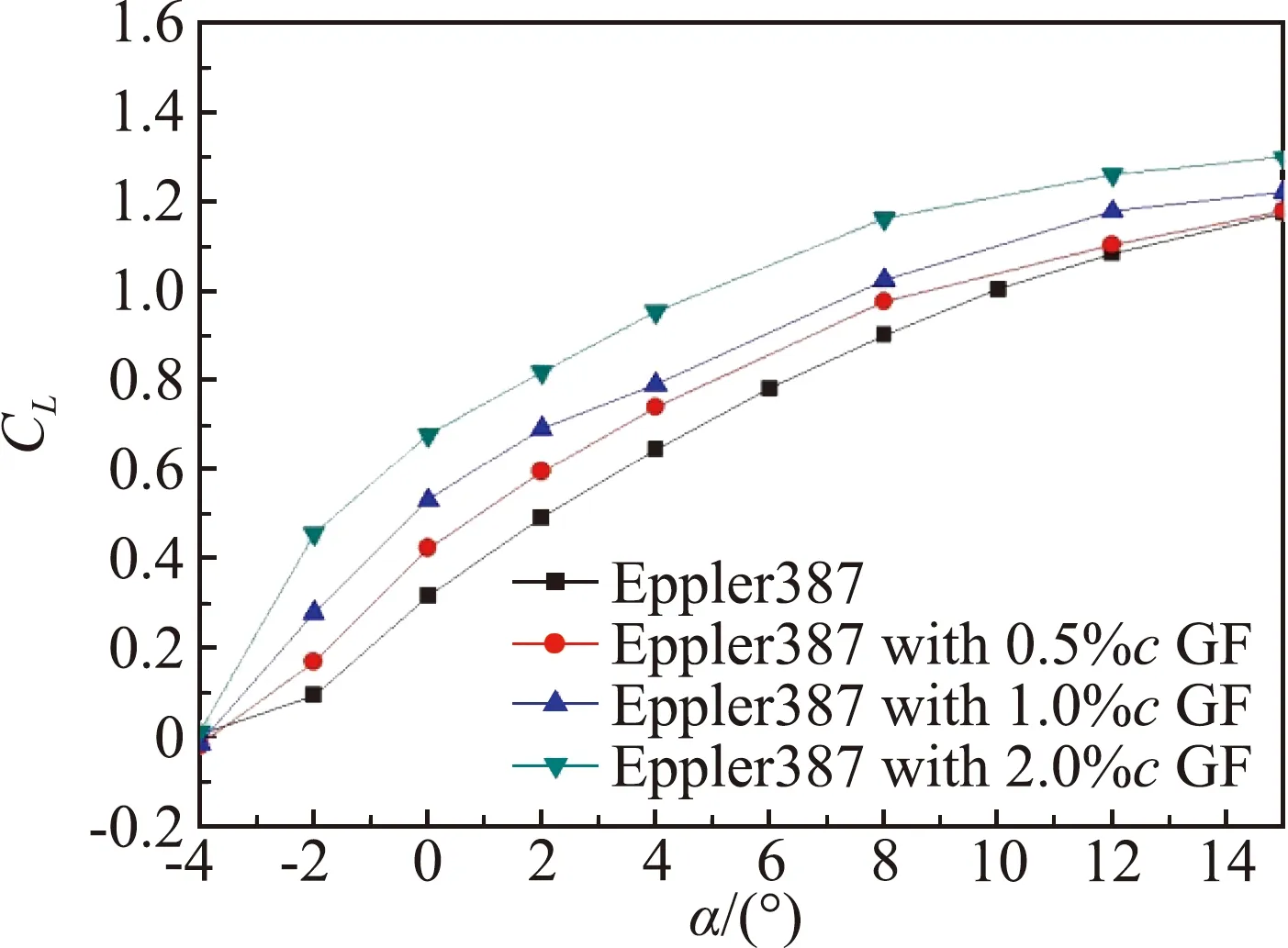
(b)Ma=0.8

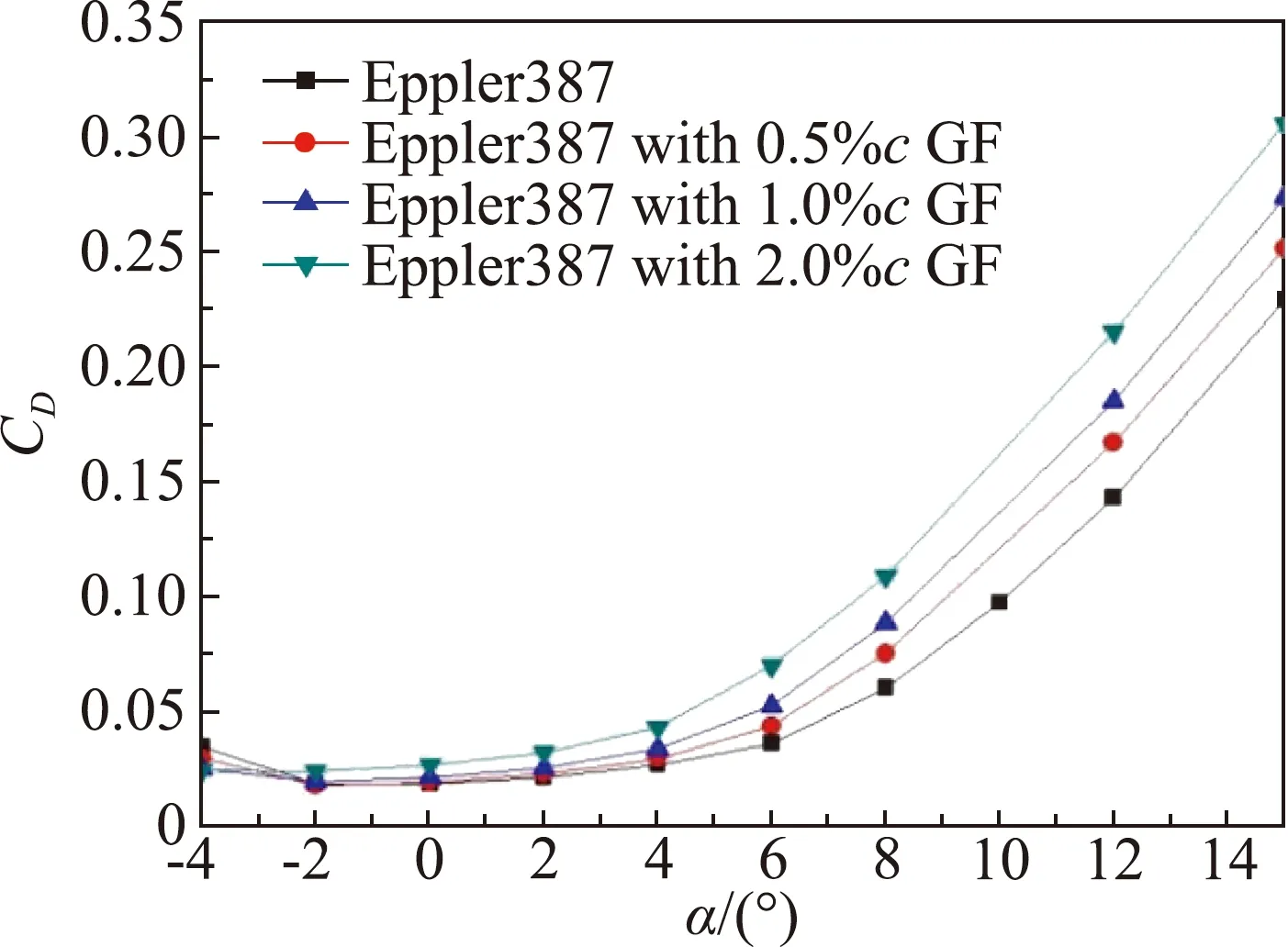
(a)Ma=0.6

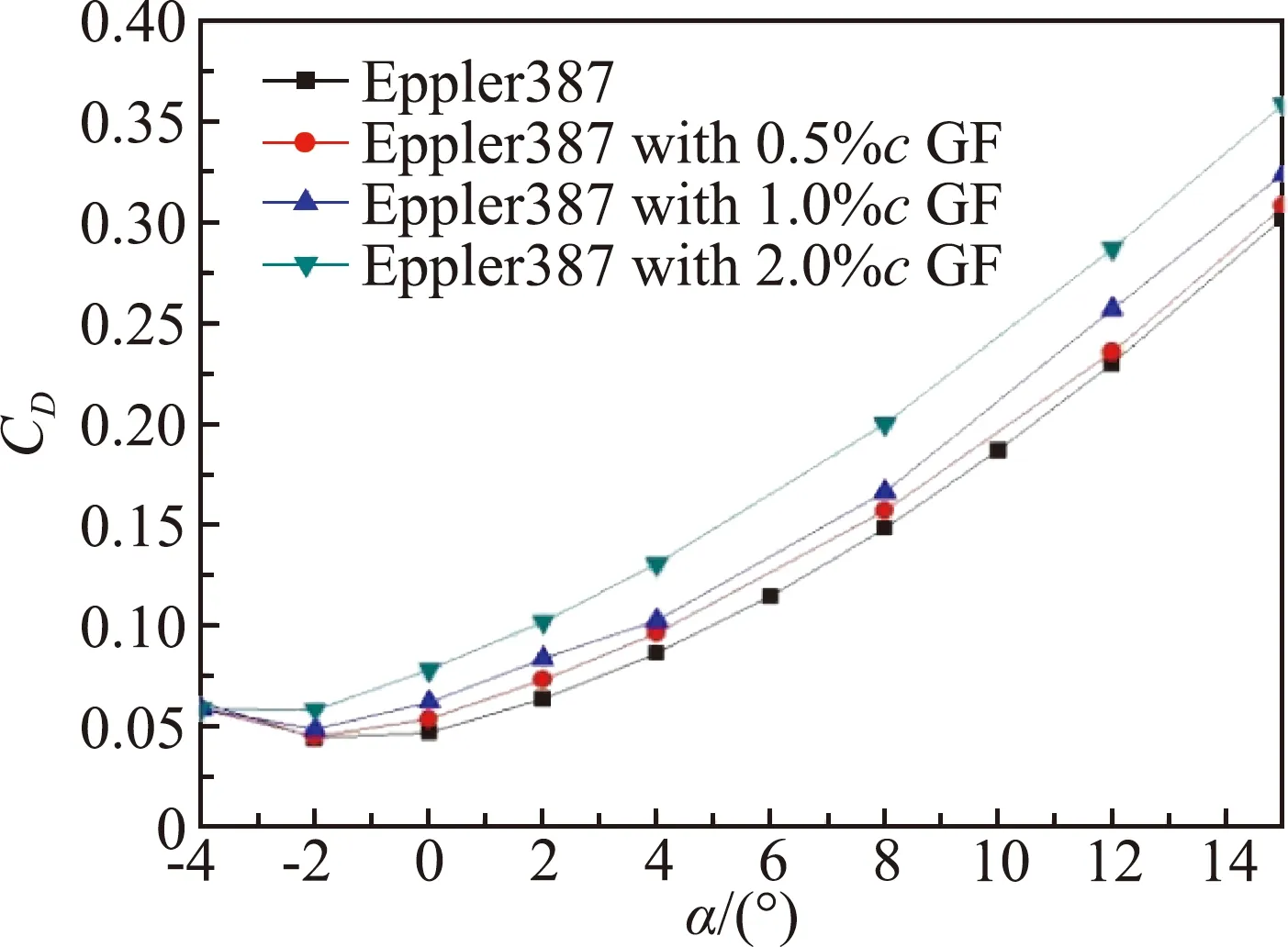
(b)Ma=0.8

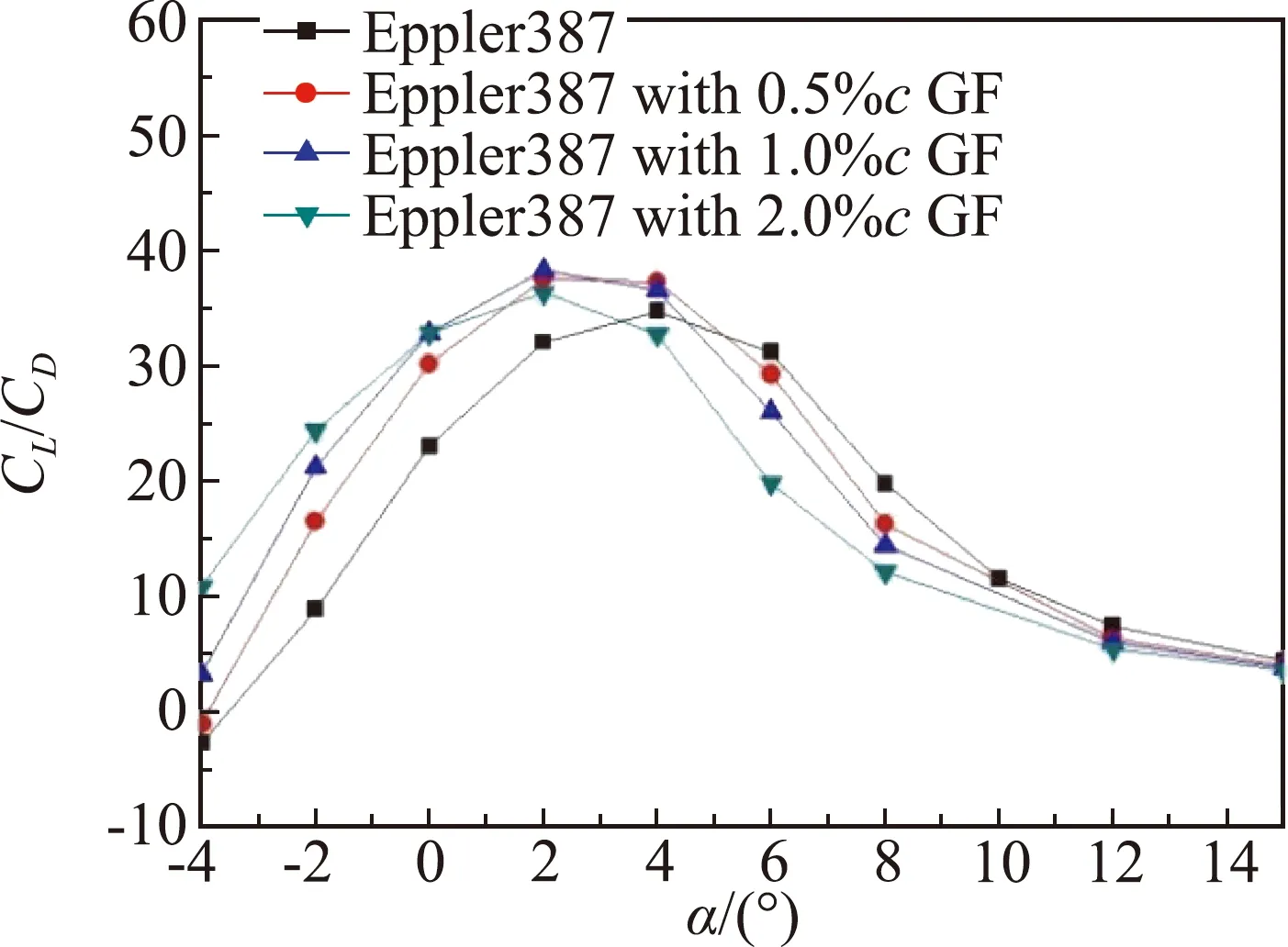
(a)Ma=0.6

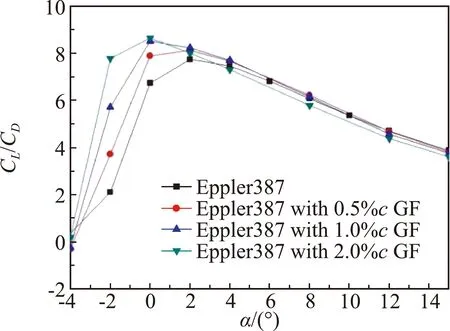
(b)Ma=0.8

图11中加装格尼襟翼后，在迎角小于6°时翼型阻力系数略微增大，超过失速迎角后翼型阻力快速增加，2%c襟翼的阻力增加最多。在马赫数0.8时，翼型阻力明显表现出了随襟翼高度增加而增大的趋势。

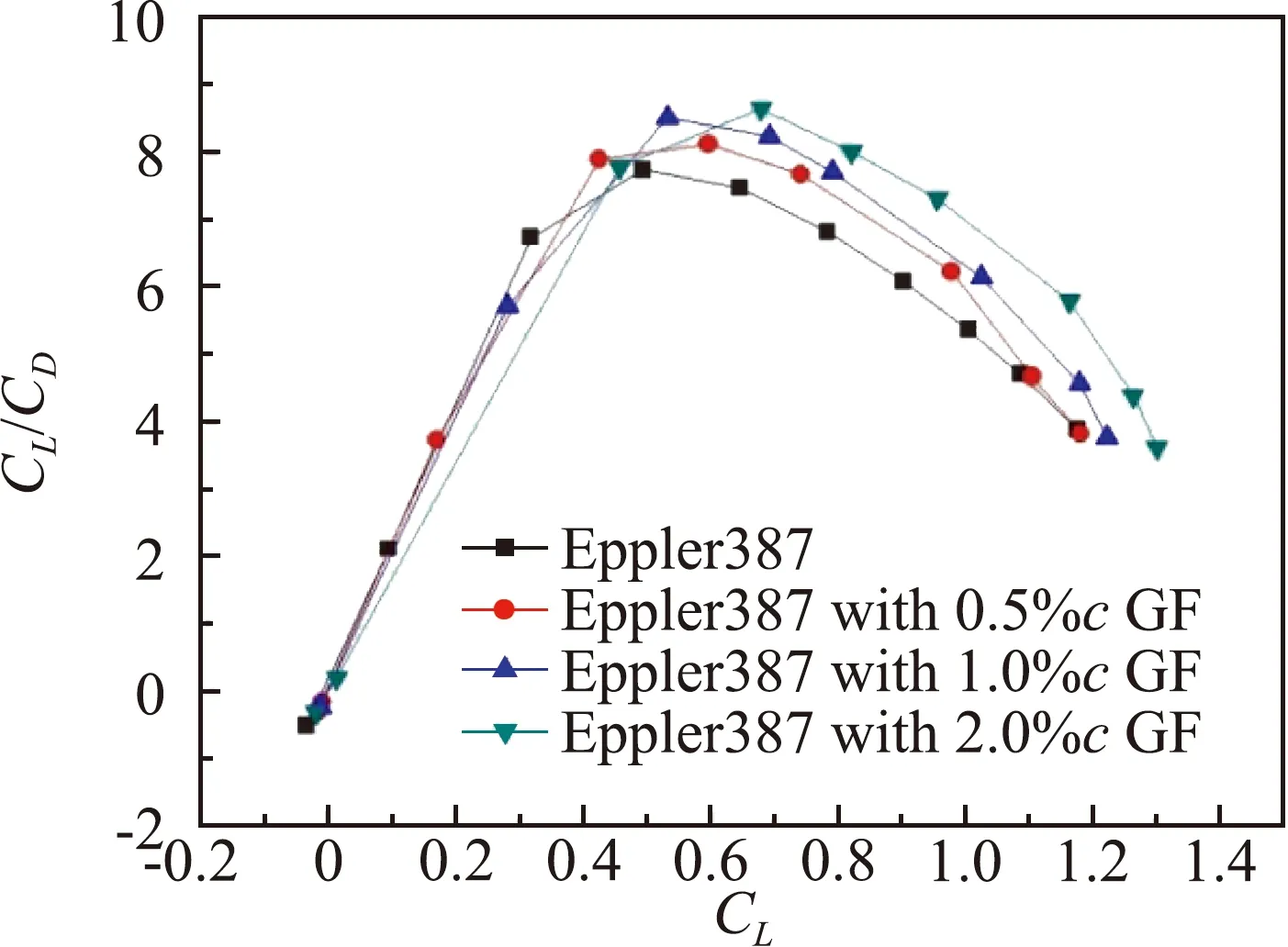
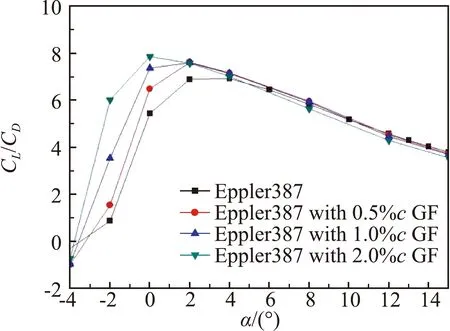
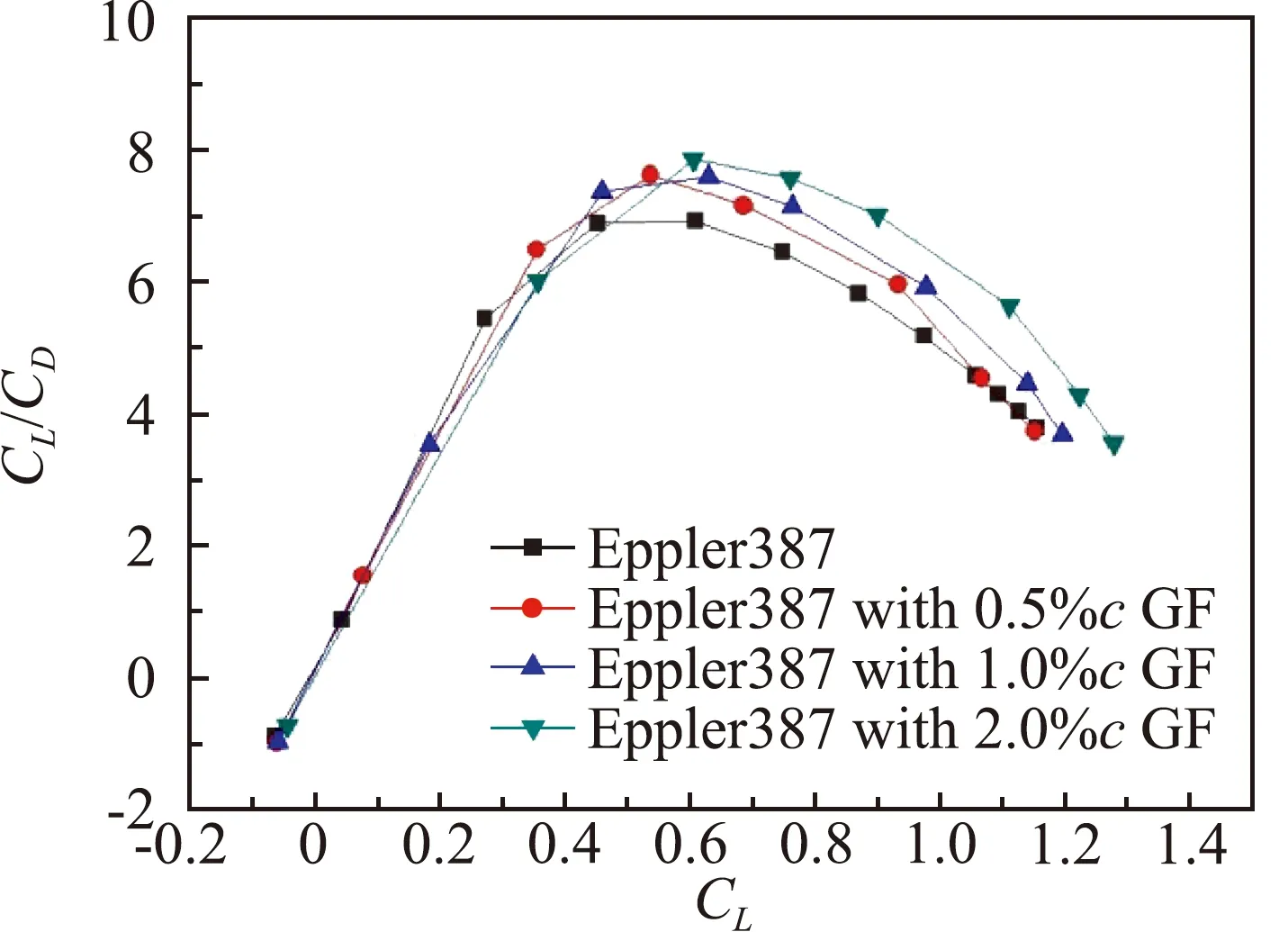
图12(a)中在马赫数0.6下，当迎角小于4°时格尼襟翼能够增大翼型的升阻比，在中高迎角下格尼襟翼使翼型升阻比减小，其中0.5%c和1%c格尼襟翼明显提高了翼型的最大升阻比。图12(b)表明在马赫数0.8下，0.5%c和1.0%c格尼襟翼在-2°～12°迎角范围内均能增大翼型的升阻比。

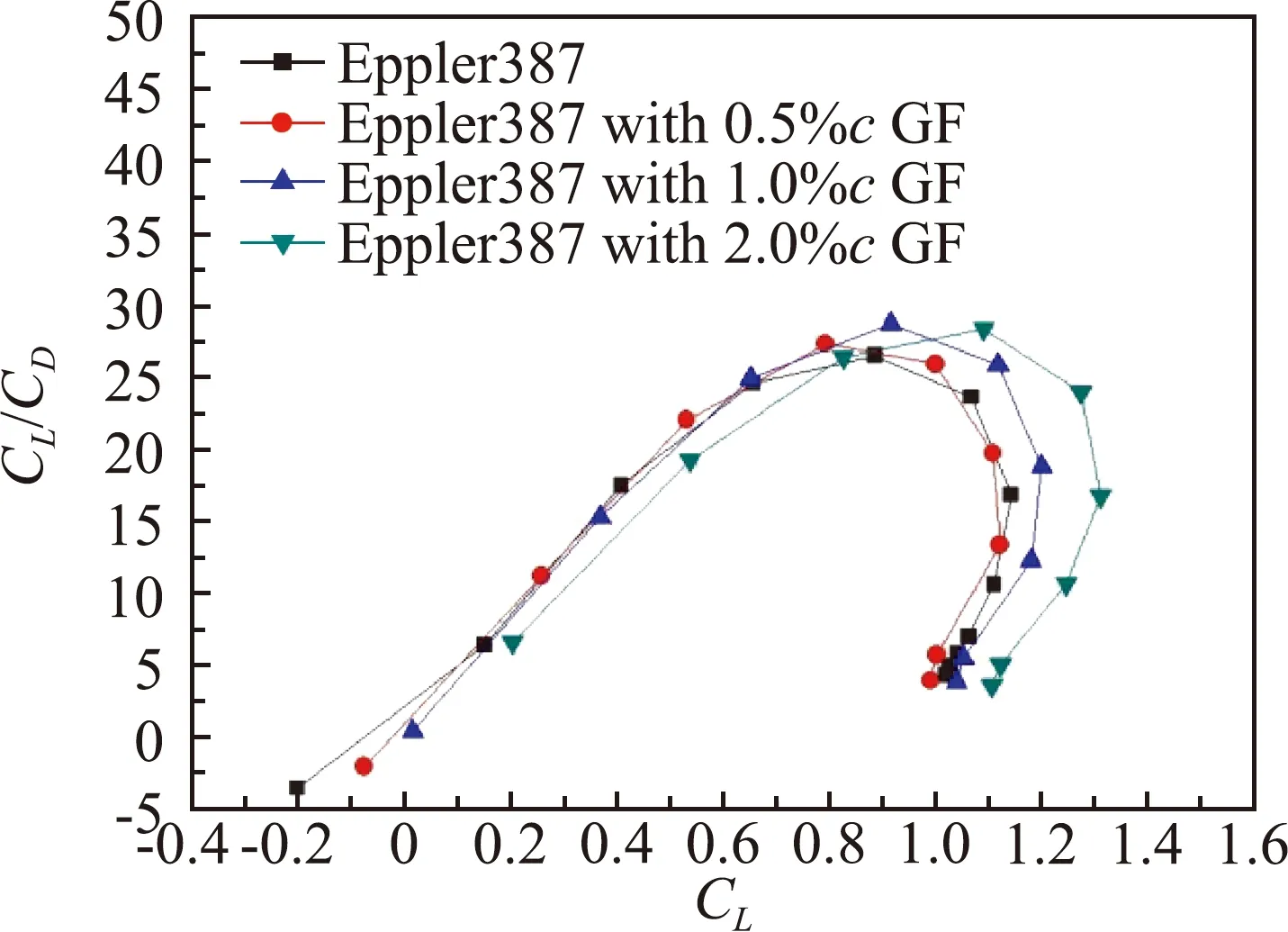
图13为相同升力系数下翼型的升阻极曲线。0.5%c和1%c格尼襟翼在小升力系数下能够保持与原翼型相当的升阻比，在中高升力系数下能够显著增大翼型的升阻比。马赫数越大格尼襟翼的增升效率越高。图14～图16是雷诺数为0.5×105时，不同马赫数下翼型加装格尼襟翼的计算结果。计算表明,在更小的雷诺数下，翼型的最大升阻比减小，格尼襟翼所体现出的增升减阻效果略有下降，但气动性能总的变化趋势，与雷诺数为1.0×105时类似。

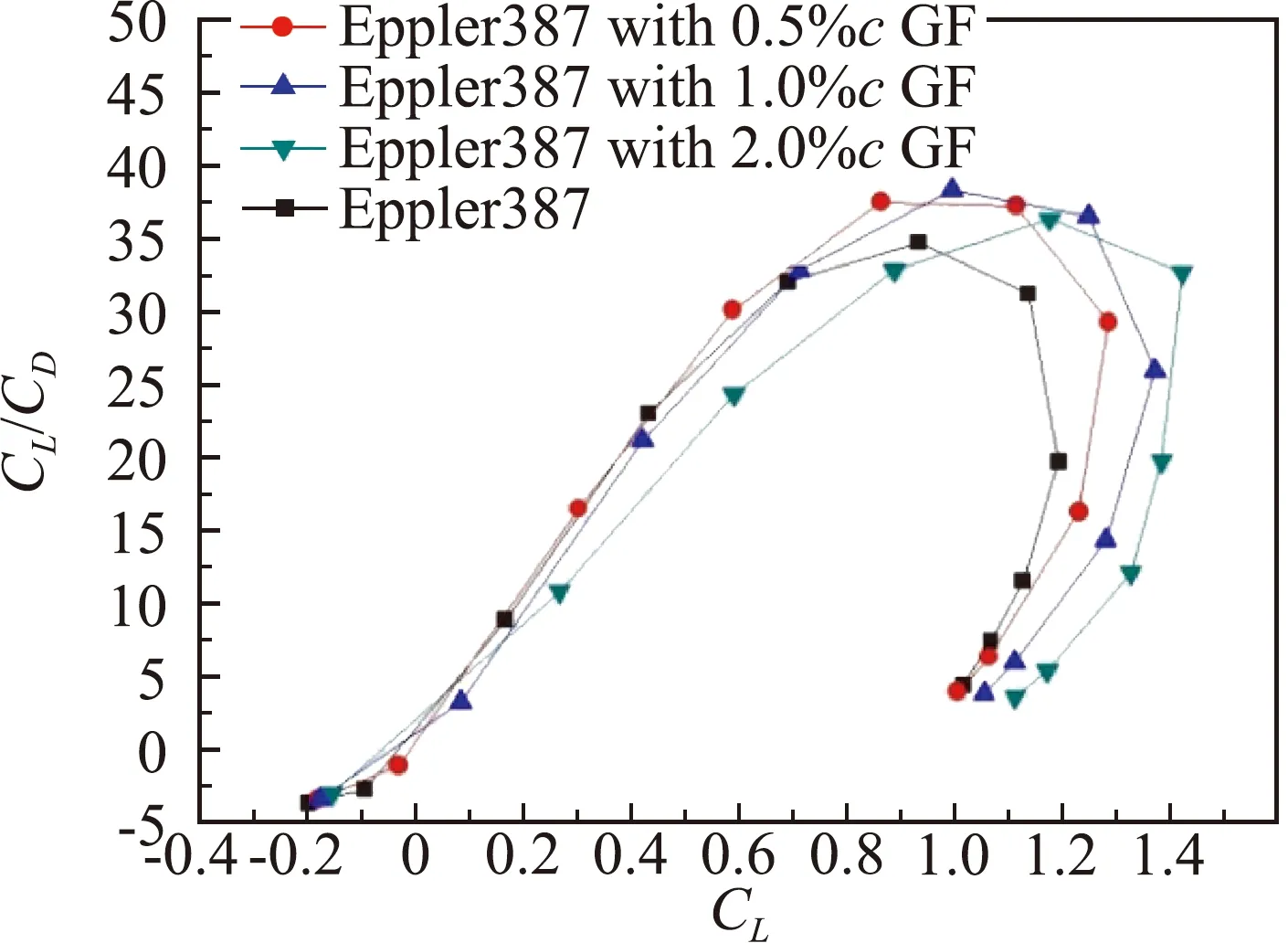
(a)Ma=0.6

(b)Ma=0.8

(a)Ma=0.6

(b)Ma=0.8

(a)Ma=0.6

(b)Ma=0.8

(a)Ma=0.6

(b)Ma=0.8

4 结 论

1)在低雷诺数、跨声速的特殊气动条件下，Eppler387翼型加装格尼襟翼后，前缘吸力和翼型上下表面的压差增大，即增大了翼型环量。这是加装格尼襟翼后翼型增升的主要原因。

2)低雷诺数、跨声速条件下，格尼襟翼使上表面激波位置略有推迟，同时削弱了下表面激波，有利于低雷诺数翼型的增升减阻。

3)高马赫数时格尼襟翼不但显著增大了翼型的升力系数，还能提高翼型的最大升阻比。马赫数0.8时加装格尼襟翼后，几乎在全迎角范围内翼型的升阻比增大。

4)临近空间和火星表面为典型的低密度大气条件，飞行器主要面临低雷诺数、跨声速的气动环境。常规低雷诺数翼型也许并非是该条件下最优的设计方案，高效增升减阻技术有利于改善常规翼型在此条件下的气动性能。目前主要基于数值计算技术开展相关研究，如何构建雷诺数、马赫数相似的地面试验条件，将是该气动领域研究进一步研究与发展方向。