旋转开槽圆筒式阵风发生器流场特性数值模拟

向正平, 戴玉婷,*, 黄广靖

(1.北京航空航天大学 航空科学与工程学院, 北京 100191;2.北京航空航天大学 航空器先进设计技术工业和信息化部重点实验室, 北京 100191)

0 引 言

飞机在飞行过程中，经常会受阵风的影响而发生颠簸，严重时会导致飞机损坏甚至发生较为严重的事故[1]。因此，飞机必须通过阵风响应检验才能交付使用，而合理确定阵风载荷并减缓阵风影响对于确保飞机飞行安全具有重大意义[2-4]。近年来，杨俊斌、吴志刚[5]等利用能产生连续正弦阵风的叶栅型阵风发生器，设计风洞试验，对大展弦比飞翼布局的飞机开展了阵风减缓主动控制试验研究。宗宁[6]开展了阵风载荷减缓风洞验证试验，验证载荷减缓方案设计的有效性。DAI Y T[7]等对飞机模型阵风减缓方法的鲁棒性进行了试验和理论研究。

以上研究表明阵风发生器是研究阵风响应和阵风减缓的必备装置，其作用是在风洞里模拟阵风，并作为飞机防阵风设计的试验装备，在国内外得到了有效发展[8-10]。传统阵风发生器有叶栅型阵风发生器[11]、级联式震荡翼型[12]、带摆动襟翼的固定翼型[13-14]、带震荡喷射襟翼的固定翼型、带有循环控制的翼型[15]等，目前应用比较广泛的为叶栅型阵风发生器。这些传统的阵风发生器存在高频振动明显、机械控制复杂、所需电机功率较大等缺点。因此需要机械控制简单、可靠性高的新式阵风发生器。而旋转开槽圆筒式阵风发生器在很大程度上弥补了传统阵风发生器的不足，具有独特的优点。目前该型阵风发生器主要用于低速风洞试验。

旋转开槽圆筒机构最早用于颤振激励，而后用于阵风发生器机构。在颤振激励方面国内研究较多，许和勇[16]等对这种新型颤振激励系统的特点提出了一种高效、简便的动网格方法，计算了该激励系统工作时的非定常气动力特性。王涛[17]等研究了该激励系统的工作原理和激励力特性。杨智春[18]等研究了该系统的静态和动态气动特性。刘志荣[19]等研究了开缝圆柱缝隙倾斜角对脱落涡的影响。D.M.Tang[8]等对该型阵风发生器做了理论和试验研究，分析了阵风产生的机理及阵风与圆槽旋转频率之间的关系。

以上研究工作主要集中在开缝圆柱机构附近的流场特性。且作为阵风发生装置，尽管理论研究和试验研究取得了巨大进步，但该装置若要成功应用于风洞试验，还有许多问题有待研究。本文研究的主要目的是分析该装置在下游产生的流场幅值和频率特性，研究结果对于该型阵风发生器试验装置的合理设计具有一定意义。

1 旋转开槽圆筒式阵风发生器

旋转开槽式阵风发生器装置的几何结构如图1所示。为满足阵风幅值要求，该阵风发生器由四片相同的叶片组合而成[20]。每片叶片由一个可旋转的开槽圆筒和固定直机翼组成。当流体流过机翼并经过旋转的开槽圆筒时，在圆筒后缘会产生类似正弦变化的阵风。机翼的升、阻力系数与圆筒旋转的角度、圆筒到机翼尾部的距离及圆筒的开槽角度有关[21]。忽略两叶片之间的干扰,选取一片叶片建模，进行流场分析。由于叶片的截面相同且机翼和圆筒较长,故可用二维模型来模拟。二维模型图如图2所示。翼型为NACA0012对称翼型，弦长c=305 mm，翼型尾部到圆筒左端距离e=24.4 mm，圆筒外径76.2 mm，厚度9.6 mm，开缝角度90°。

图1 阵风发生器装置

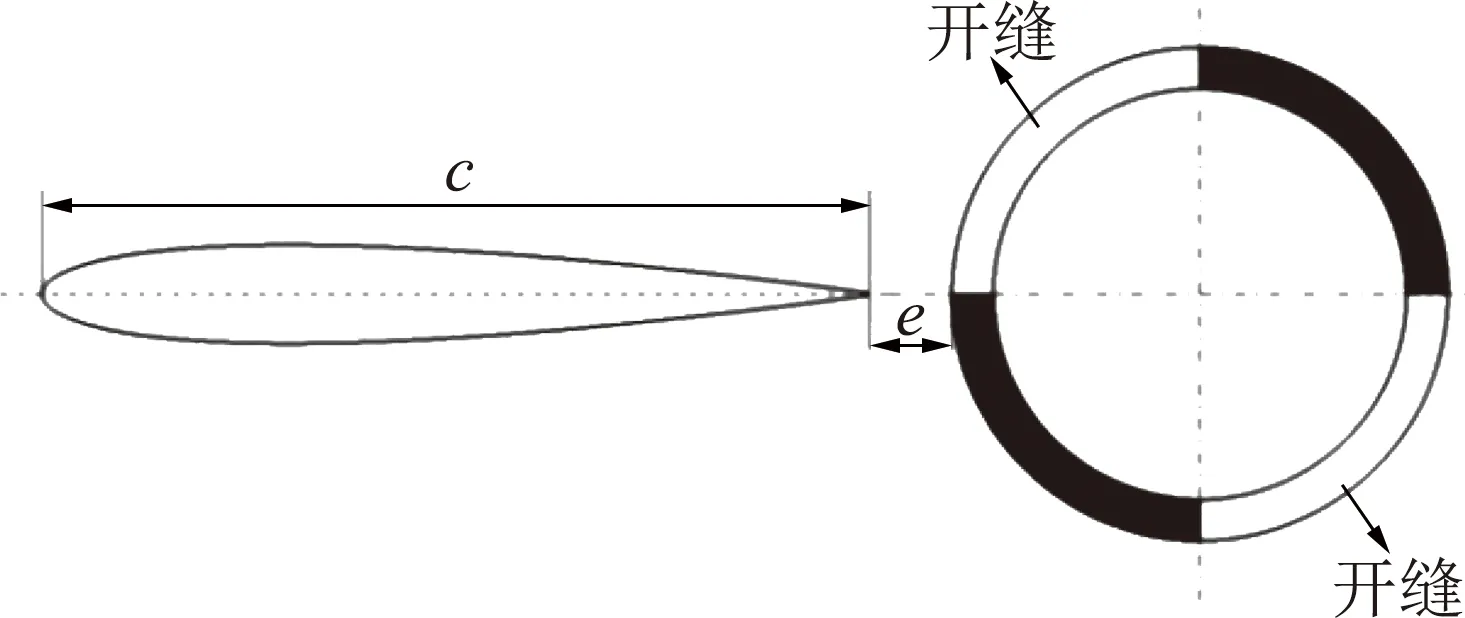
图2 单片叶片的二维模型图

2 计算网格和方法

2.1 网格划分

采用OpenFOAM开源CFD软件来建模和数值分析。OpenFOAM是一个在Linux系统下运行的CFD类库。它是一个完全由C++编写的面向对象的CFD类库，支持多面体网格，可以处理复杂的几何外形。研究人员可根据需要编写自己的求解器。这里采用了OpenFOAM中的AMI (Arbitrary Mesh Interface)技术实现网格旋转时的数据交换，旋转角速度可设定，从而实现动态旋转的模拟过程。网格划分采用OpenFOAM中的blockMeshDict字典程序控制，划分结构网格。划分的整体结构化网格如图3所示，图4为翼型附近局部加密网格，图5为旋转圆筒部分网格。

2.2 数值计算方法

在惯性坐标系下，非定常积分形式的Navier-Stokes表达式为：

(1)

图3 整体结构网格

图4 翼型附近网格

图5 旋转圆筒处网格

其中U表示单位体积质量、能量和动量表示的通量，F和FV分别表示无黏流通矢量和有黏流通矢量，Ω(t)为运动控制体积，S(t)为运动控制体积的表面积。

采用有限体积法进行空间离散，二阶迎风格式，时间推进采用隐式方法，湍流模型为k-wSST湍流模型，该模型能很好地处理流动分离[22]。

在圆筒旋转的过程中，机翼和圆筒上会产生非定常气动力。旋转开槽圆筒阵风发生器的等效升力系数[5]计算方法为：

(2)

式中dLa、dLrsc分别为翼型和开槽圆筒上的升力，c为翼型弦长，d为圆筒外径，ρu2为动压。

3 计算结果及分析

3.1 等效升力系数计算

为准确模拟阵风发生器的下游流场特性，需首先数值模拟旋转开槽圆筒式阵风发生器的等效升力系数，与试验数据对比。图6、图7分别为圆筒旋转20°(以图2位置为起点，逆时针旋转)时的压力、速度云图。中心线位置在图6中划出，来流方向沿x轴正方向。中心线上下两侧为侧向位置，以圆筒中心为起点，沿x轴正向为下游流场。

图6 旋转角20°时的压力云图

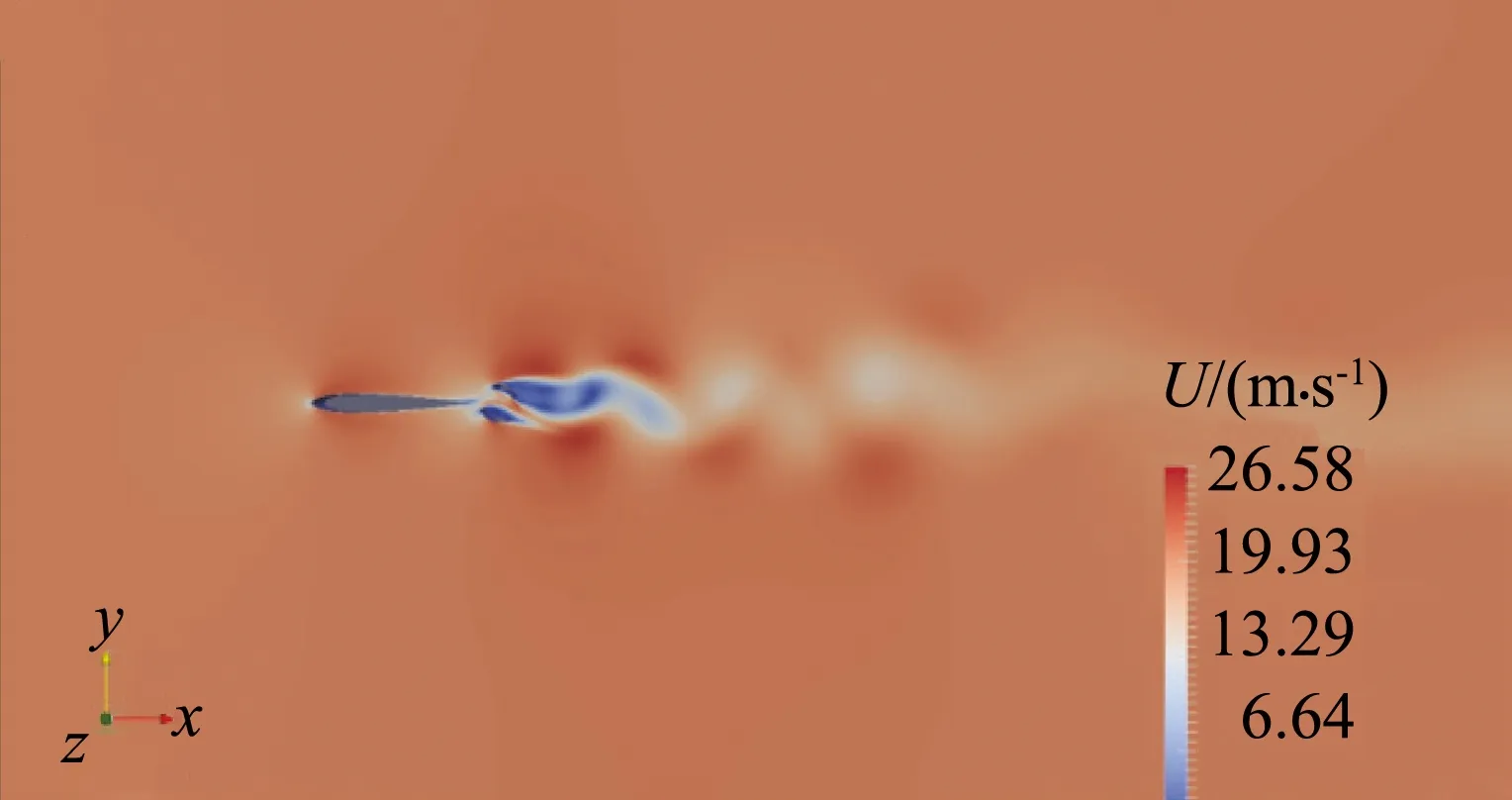
图7 旋转角20°时的速度云图

在旋转角度0°～180°范围内，数值计算获得等效升力系数与试验数据对比结果如图8所示。图中试验数据和理论数据从文献[8]中获得，OpenFOAM仿真数据为本文CFD数值模拟结果。由图可见,等效升力系数随着旋转角度的变化类似正弦变化，分别在20°左右和70°左右达到峰值，最大幅值约为0.4。结果表明CFD计算的等效升力系数与试验数据吻合较好，验证了求解器的正确性。

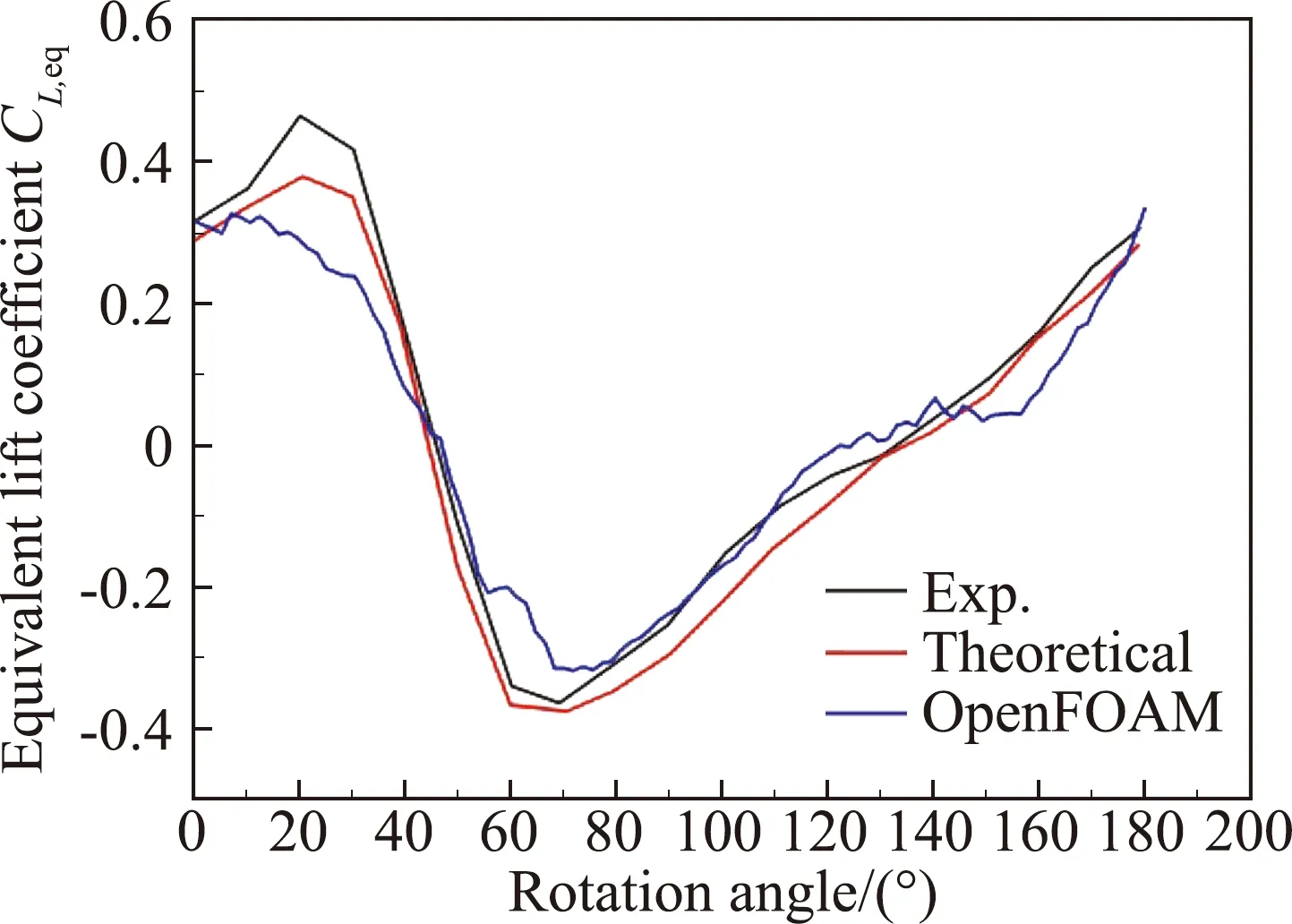
图8 等效升力系数CFD模拟值与试验数据对比

3.2 下游流场分析

3.2.1 旋转圆筒对流场的影响

首先，开槽圆筒的旋转方向对下游流场特性有明显影响。当逆时针方向旋转时，在阵风发生器下游离圆筒中心距离0.6 m处，中心线两侧等距位置处产生的阵风(y方向的扰动速度)有明显差别。以旋转频率5 Hz、来流速度20 m/s、中心线两侧0.25 m处为例，计算结果如图9、图10所示。由图可知，上侧产生的阵风比较紊乱，下侧产生的阵风正弦特性较好,阵风响应不对称是由扰动速度的初值引起的。当改变圆筒旋转方向为顺时针时，结果正好相反，中心线上侧阵风正弦特性较好，下侧比较紊乱，计算结果如图11所示。圆筒旋转方向不同导致上下产生的扰动阵风不对称，当逆时针旋转时，对上侧扰动阵风的干扰较大，阵风的正弦特性变差。当圆筒顺时针旋转时，情况正好相反。

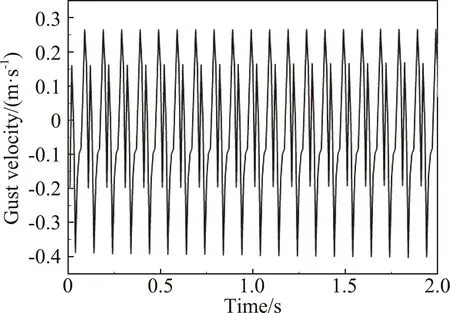
图9 逆时针旋转时中心线上侧阵风随时间响应

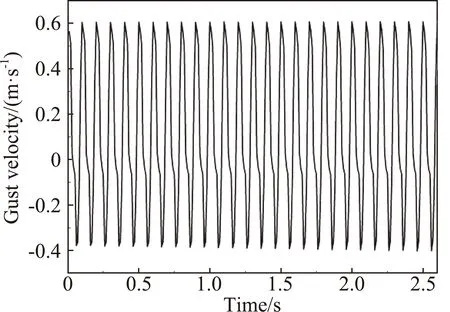
图10 逆时针旋转时中心线下侧阵风随时间响应

其次，旋转圆筒对中性线附近流场干扰明显。在中心线两侧较近的位置，离中心线侧向距离约0.2 m以内的范围，产生的阵风比较紊乱，随着远离中心线位置，阵风的正弦特性越来越好。同样以旋转频率5 Hz、来流速度20 m/s为例，在阵风发生器下游离圆筒中心距离0.6 m、中心线下侧位置0.15 m和0.35 m处，阵风随时间的响应分别为图12、图13所示。

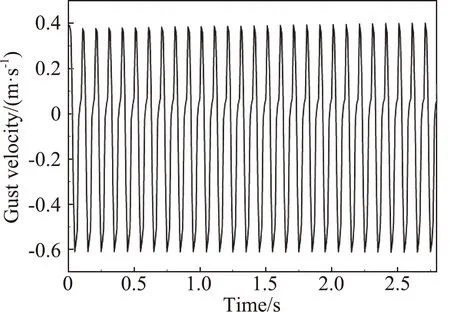
图11 顺时针旋转时中心线上侧阵风响应

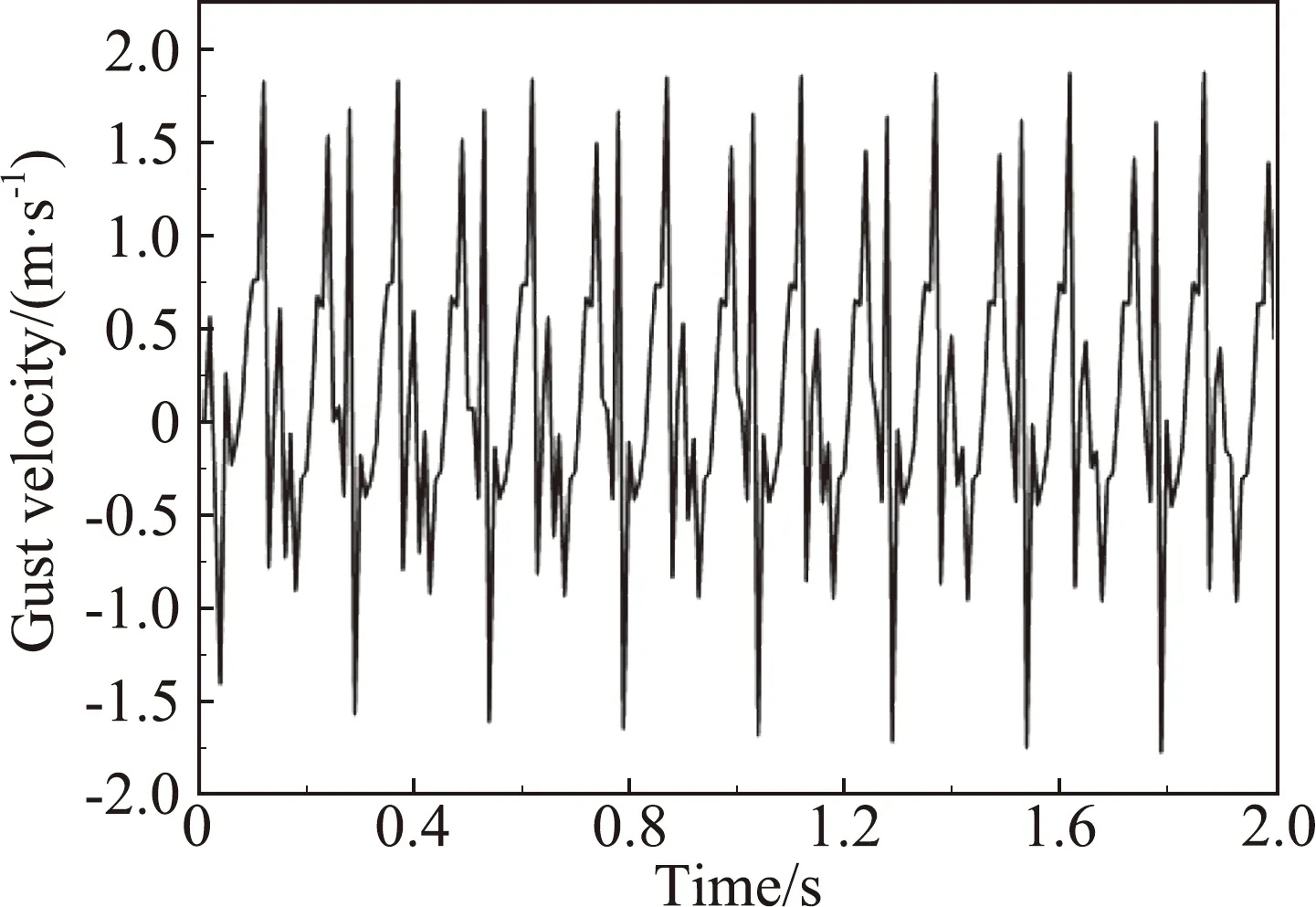
图12 中心线下侧0.15 m处阵风随时间的响应

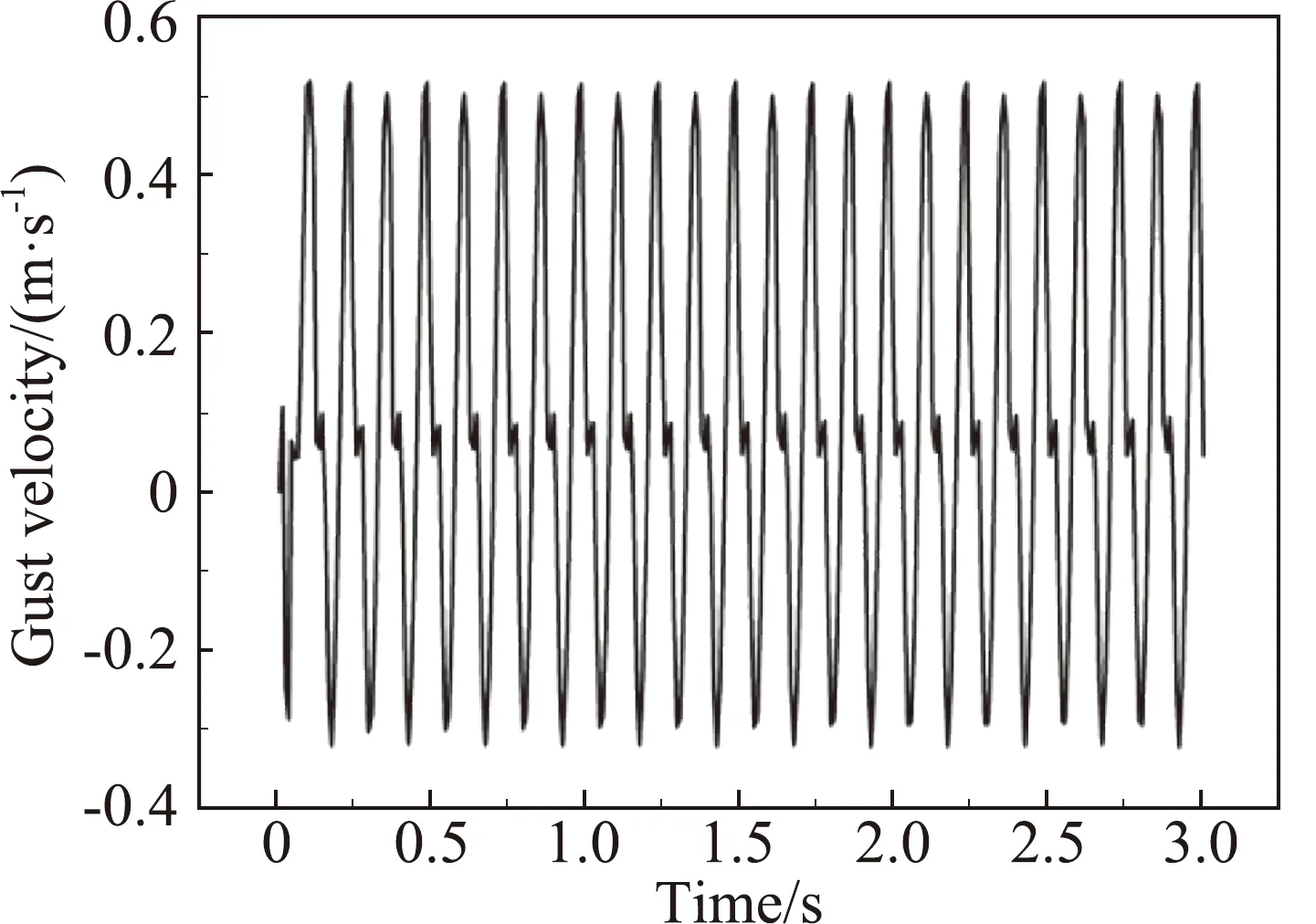
图13 中心线下侧0.35 m处阵风随时间的响应

对比图12和图13可知，虽然离中心线越近，最大阵风幅值越大，但是阵风正弦特性很差，这主要是由于开槽圆筒旋转过程中，对中心线附近的干扰比较大所致。

3.2.2 下游流场位置对阵风幅值的影响

首先，在不同旋转频率下，比较了阵风幅值随侧向距离的变化规律，比较结果如图14所示。图中分别计算了旋转频率1～8 Hz的状态，获得一致的规律，即侧向位置离中心线越远，阵风幅值逐渐递减。

其次，在不同频率下，比较了阵风幅值随下游距离的变化规律，比较结果如图15所示。图中画出了旋转频率5 Hz和6 Hz下的变化。由图可知，距离圆筒中心越远，阵风幅值逐渐递减。

以上结果表明，中心线侧向位置和流场下游位置离旋转圆筒越远，阵风幅值越小。

图14 阵风幅值随侧向位移的响应

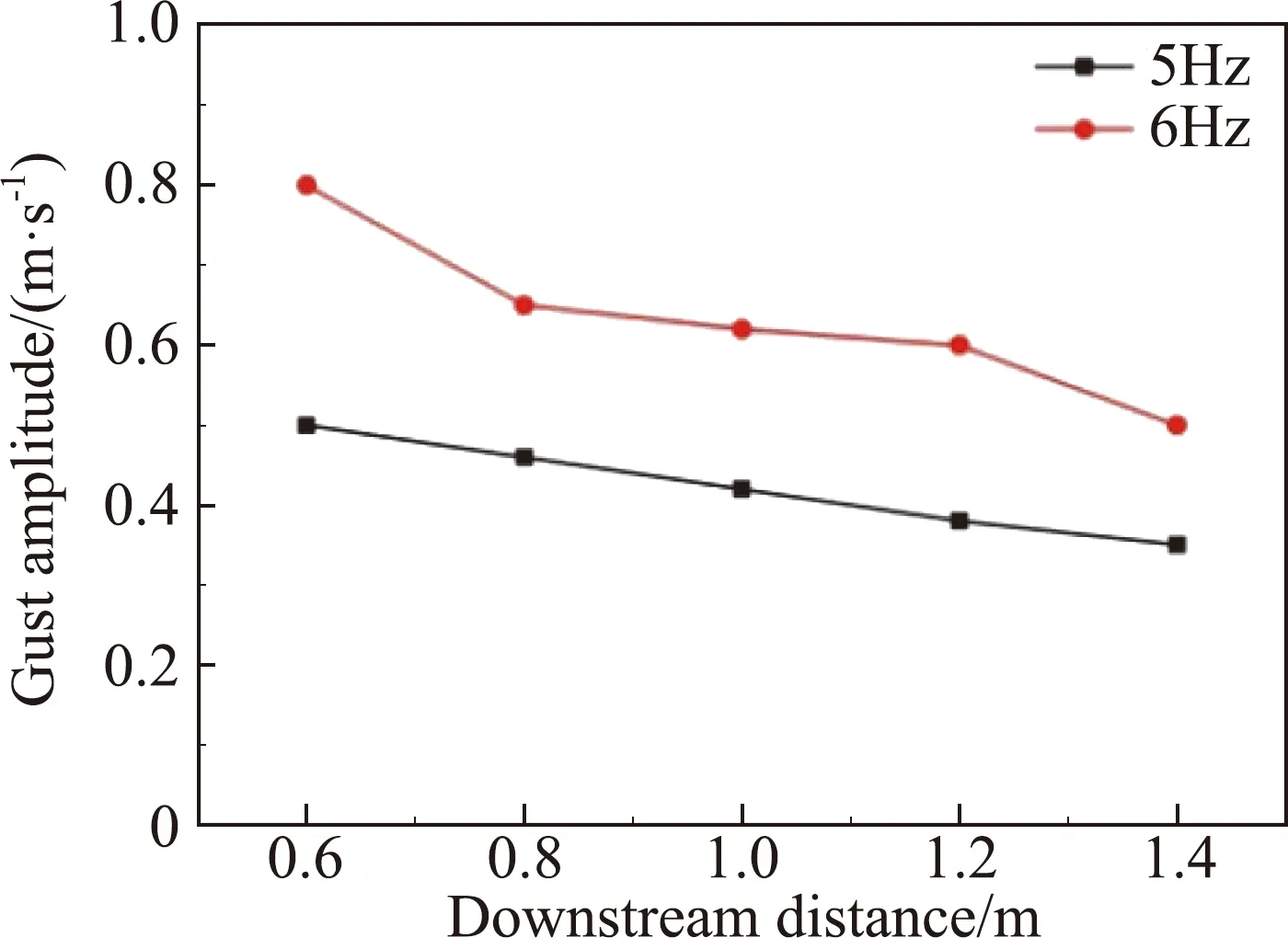
图15 阵风幅值随下游位移的响应

3.2.3 减缩频率对阵风幅值的影响

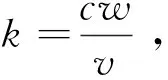
计算了在低速不同状态下的减缩频率，都获得了一致规律，但在0.2～0.25减缩频率范围内出现突变的内在机理有待进一步研究。

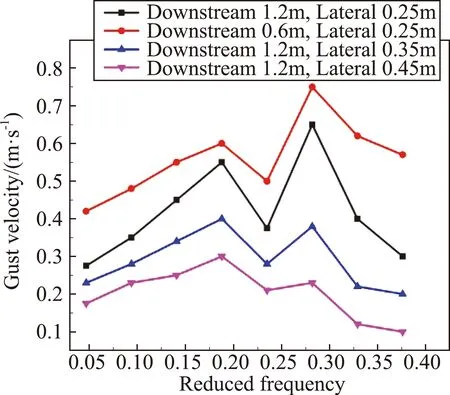
图16 阵风幅值随减缩频率的响应

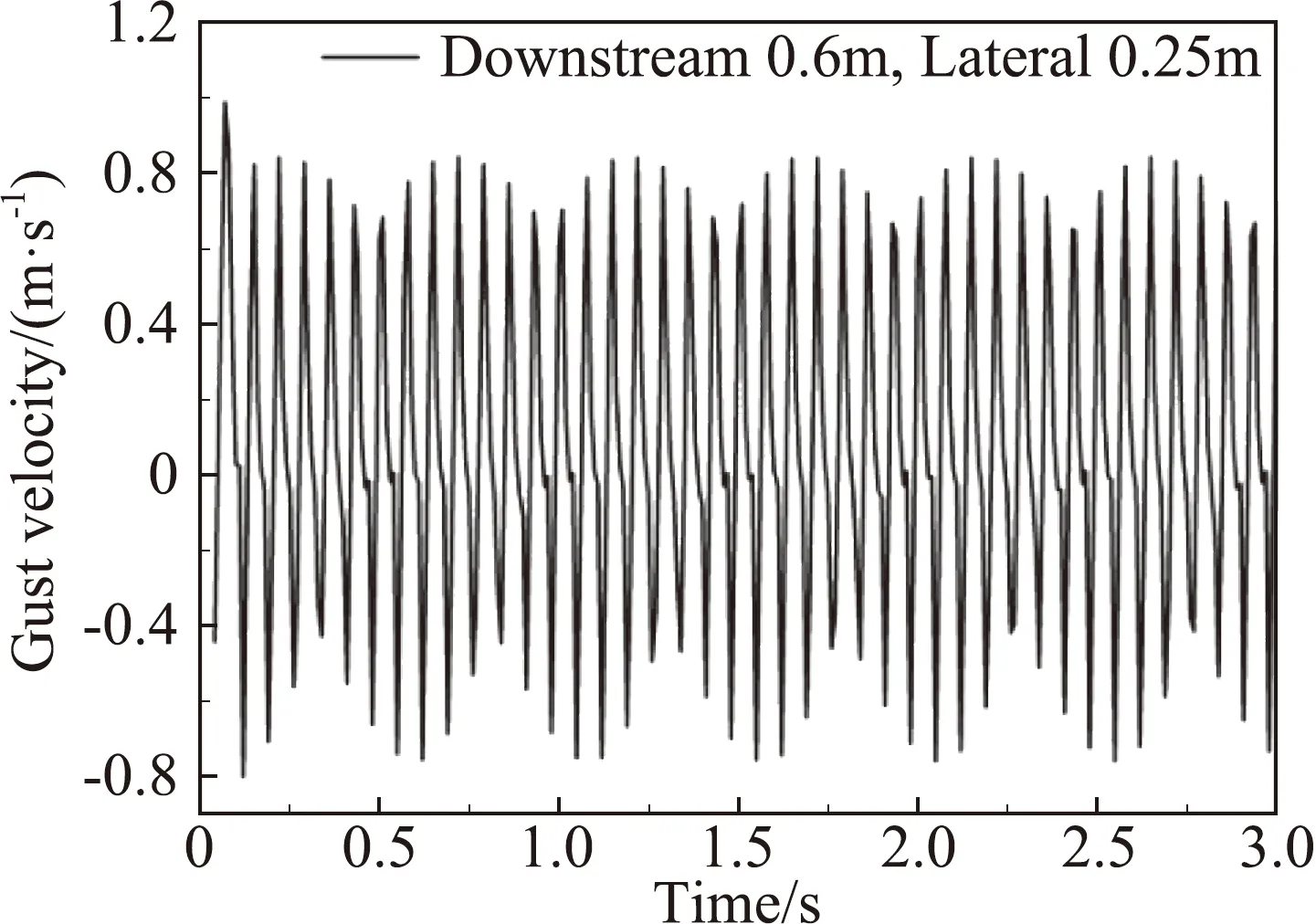
图17 频率7 Hz时阵风随时间的响应

4 结 论

通过对旋转开槽圆筒式阵风发生器进行数值模拟和流场分析，得以下结论：

1)开槽圆筒的旋转方向对中心线上下两侧流场产生不同影响，且对中心线附近的流场干扰较大。

2)侧向位置离中心线越远，阵风幅值越小，下游离圆筒中心越远位置，阵风幅值越小。

3)阵风幅值的变化与减缩频率有关，在减缩频率0.2～0.25时阵风正弦特性最佳。但对于出现突变的内在机理还有待深入研究。

从前景来看，这种阵风发生器具有耗能少、激励频率宽、幅值可控、安装方便等优点。对该型阵风发生器进行数值模拟研究，对试验装置的设计有一定的指导意义。