基于声压相消的旋翼厚度噪声控制机理
2019-12-30史勇杰徐国华
贺 祥, 史勇杰, 徐国华
(南京航空航天大学 直升机旋翼动力学国家级重点实验室, 江苏 南京 210016)
0 引 言
随着直升机在军用领域和民用领域的广泛应用,直升机噪声辐射严重的缺点越来越引起人们的重视,并且已成为直升机设计过程中需要着重考虑的问题。旋翼噪声是直升机噪声中影响最重要的部分,按形成原理它可分为厚度噪声、载荷噪声、桨-涡干扰噪声和高速脉冲噪声等[1]。其中,旋翼厚度噪声主要沿桨盘平面向外传播,且低频成分多,因而厚度噪声具有衰减慢、传播远的特性。当直升机前飞时,桨盘平面前倾,使得旋翼厚度噪声成为远场噪声的主要构成部分,对于军用直升机来说成为影响声隐身性能的关键因素。因此探索有效降低旋翼厚度噪声的控制方法,具有重要的研究意义和广泛的应用前景。
在过去的数十年间,国内外研究人员针对旋翼气动噪声的降噪开展了一系列研究。一些研究者通过对旋翼的优化设计,如降低旋转马赫数[2]、改变桨叶外形设计[3-5](桨尖后掠、桨叶尖削或薄翼型)等,在一定程度上降低了旋翼噪声。但是,这类被动设计方法在降低噪声的同时也影响到旋翼的气动性能,进而需要在抑制噪声和保证性能之间进行折衷,由此对于旋翼厚度噪声的降噪效果也较为有限,同时还存在不同飞行状态的适应性问题。近年来,研究者们在噪声主动控制技术理论和试验方面开展了较深入的探索,但主要集中于旋翼桨-涡干扰噪声的控制[6-8],而关于旋翼厚度噪声降噪的理论和试验研究开展的较少。噪声主动控制方法包括有源相消、声压相消等,后者是通过产生一个与噪声相位相同且幅值相反的可控声波,通过叠加从而抵消某一方向上的声压脉冲。2008年,美国马里兰大学的Schmitz等[9]通过推导FW-H方程的单/偶极子项,得到了旋翼厚度噪声和载荷噪声的解析模型,并分析了运用单极子或偶极子进行旋翼厚度噪声降噪的效果[10-11]。研究表明,在桨叶外端布置单极子源可以显著地降低厚度噪声,但这种方法能量需求过大,不具备可行性,而采用偶极子降噪则成为一种较为可行的方式。Yu[12]、Brooks[13]等在桨-涡干扰噪声的主动后缘襟翼控制试验中发现,在桨盘平面内某些方位角处的旋翼厚度噪声降低得较为明显,经过分析,这可能是由于主动后缘襟翼产生的平面内阻力诱发了可以抵消旋翼厚度噪声的抑制声波。王阳等[14]针对声压相消方法开展了理论研究,提出了利用旋翼和尾桨噪声相互叠加的降噪方法,并将其应用到单旋翼直升机的降噪中。
在前人的研究基础上,本文基于声压相消原理,通过在旋翼桨尖布置阻力激励器的方式,添加面内、非定常控制力,建立了一套适用于旋翼厚度噪声降噪的控制方法,通过数值模拟,研究了噪声控制机理和参数影响规律。文中首先建立了基于FW-H方程的旋翼厚度噪声控制数值计算方法,分析了厚度噪声的构成及参数影响规律。接着分析了悬停状态下桨尖控制力的降噪特性及参数影响规律。最后,采用阻力激励器的形式实现桨尖控制力的添加,并分别开展了悬停及前飞状态下阻力激励的降噪特性研究。
1 控制模型及数值计算方法
1.1 控制模型
针对旋翼厚度噪声的传播特点以及直升机噪声的降噪需求,本文提出的控制方案是在桨叶外端布置可变面积的阻力激励器,通过控制系统使其产生的桨盘面内阻力按照特定的规律变化,进而产生可以抵消旋翼厚度噪声的抑制声波。控制模型如图1所示,通过主动驱动机构改变阻力激励器的迎风面积,从而实现不同变化规律的桨尖控制力。施加非定常控制力后远场观测点噪声的控制方程可以表示为:
(1)
式中:x为声压观测点位置,Mr是旋翼在声传播方向上的马赫数,vn是积分面运动速度,r为声源点X到观测点Y的距离,ρ0和a0分别为空气密度和声波在空气中的传播速度,下标ret表示方程中的积分计算是在延迟时间τ=t-|X(t)-Y(t)|/c上进行,F为桨尖控制力。
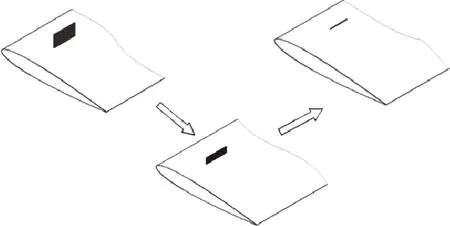
(b)阻力激励器迎风面积变化
1.2 计算方法
噪声控制方程(1)的求解采用积分形式的Farassat 1A公式[15-16],可以得到声压控制方程为:
p′总(x,t)=p′T(x,t)+p′F(x,t)
(2)

(3)

(4)
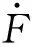
文中旋翼噪声的计算采用了本课题组发展的气动噪声分析程序RADAS(Rotorcraft Aerodynamics and Aeroacoustics Solver)。该方法已得到验证,并广泛应用于旋翼、尾桨、旋翼/尾桨干扰等噪声的计算[17-18]。本文在原有方法的基础上,采用紧致声源假设,增加了非定常控制力引起的载荷噪声项,并在程序中添加了平面内阻力的时间导数项。
2 厚度噪声参数影响分析
以AH-1/OLS模型旋翼为研究对象,桨叶几何参数如表1所示,旋转桨尖马赫数MH=0.65,声压基准观测点坐标为(-100R,R,0),以直升机正前方区域(-60°≤ψobs≤60°,-60°≤θobs≤60°)为目标观测区域(ψobs表示观测方位角,右侧为正;θobs表示俯仰角,向上为正)。

表1 算例旋翼的几何参数
2.1 厚度噪声特性
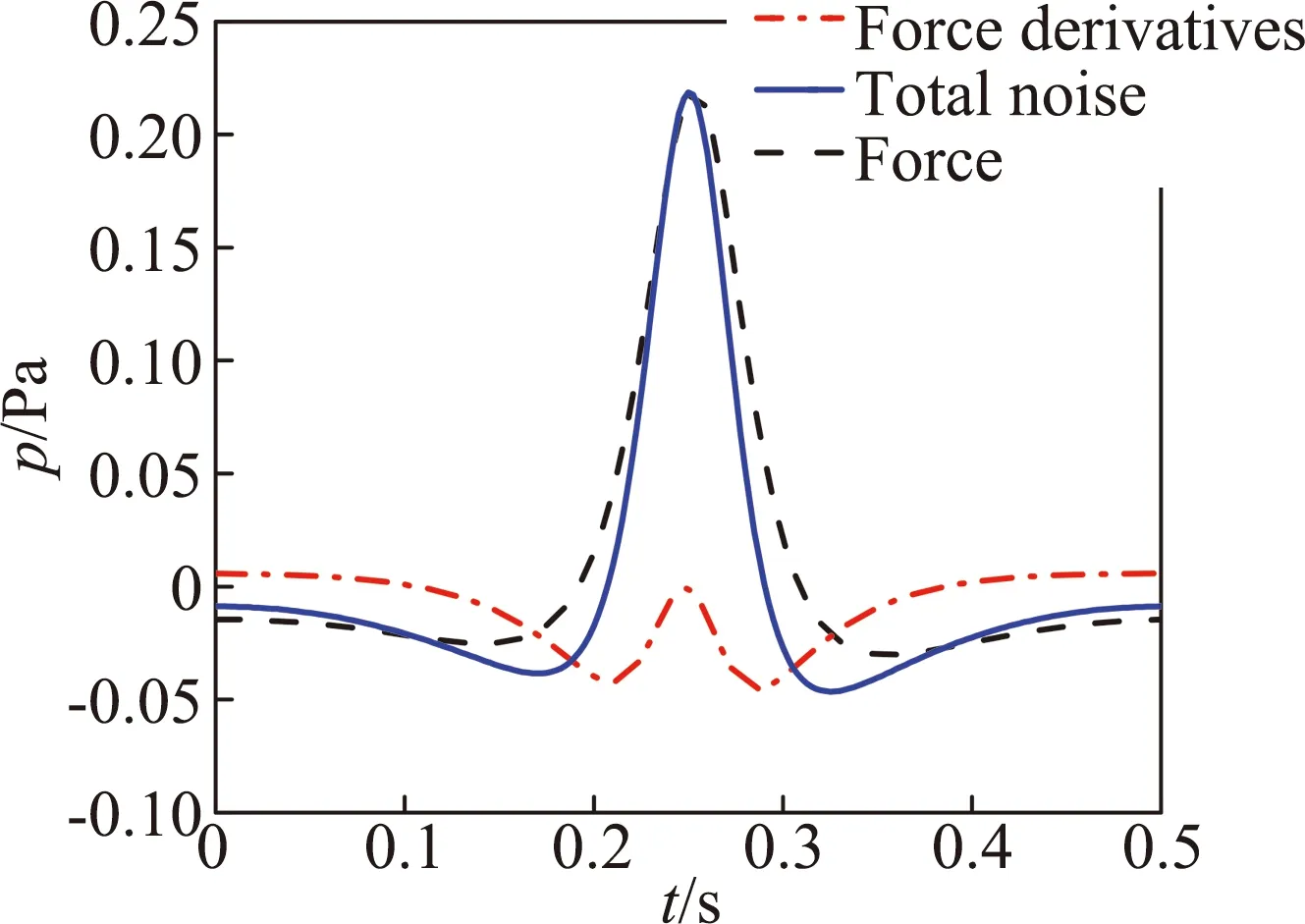
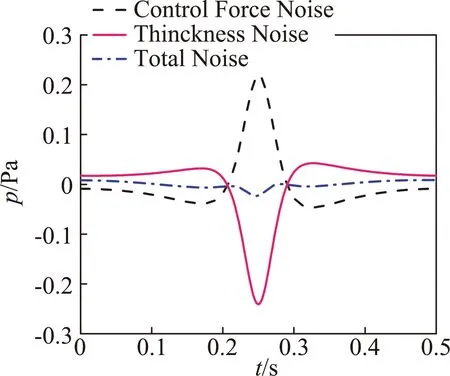
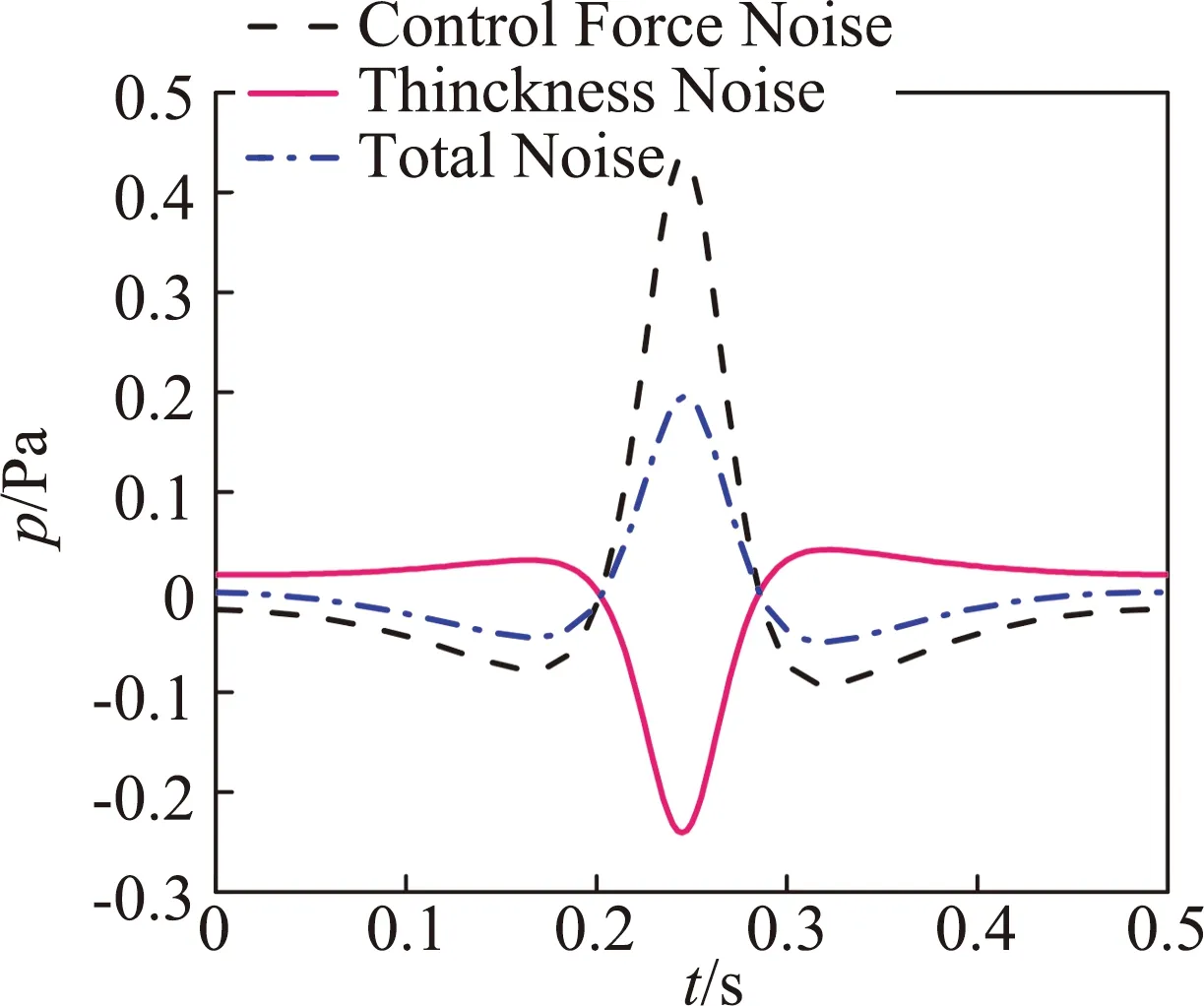
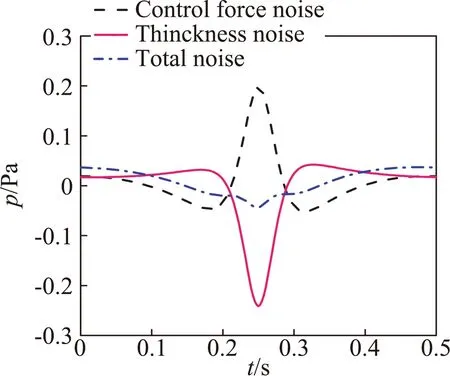
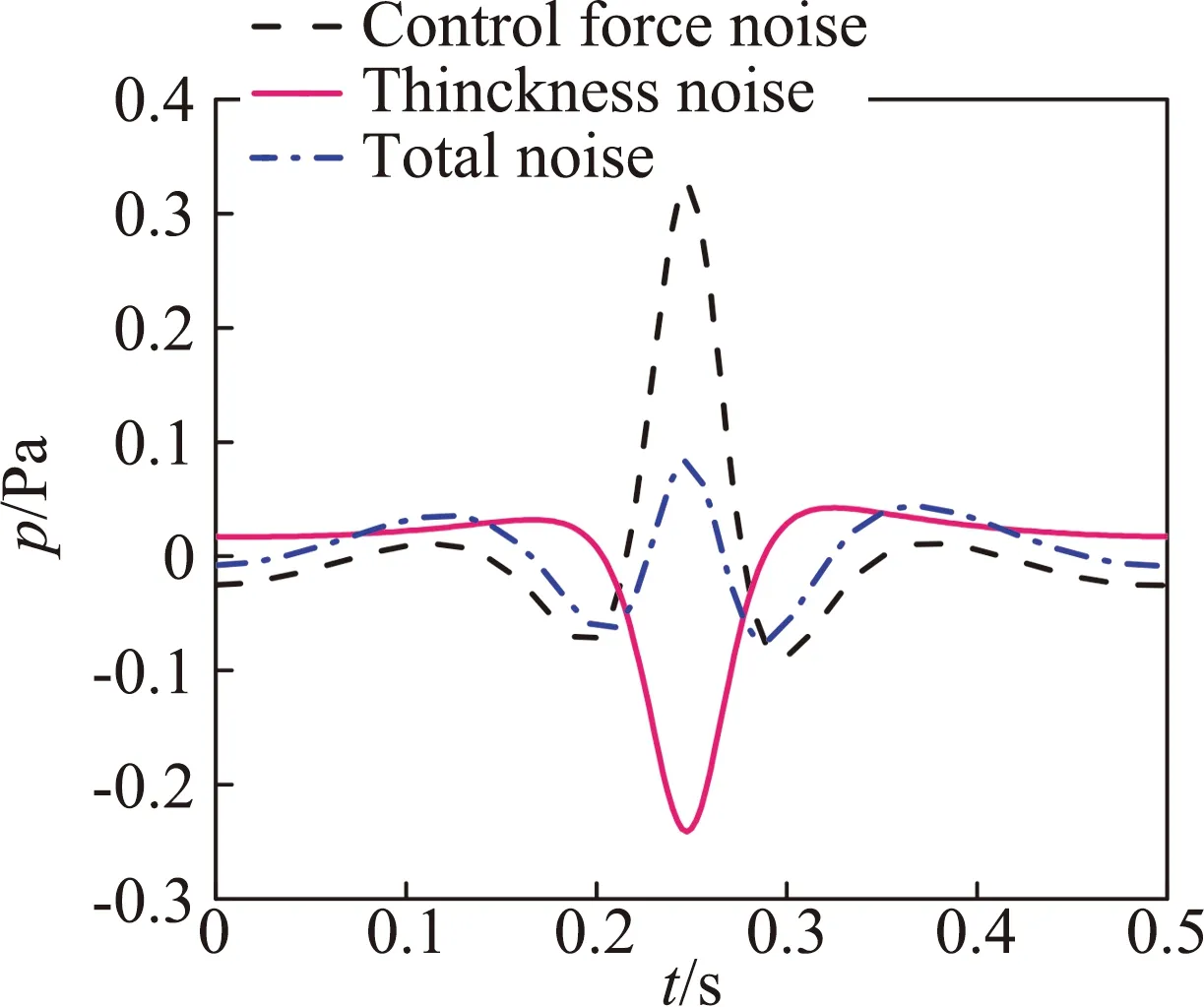
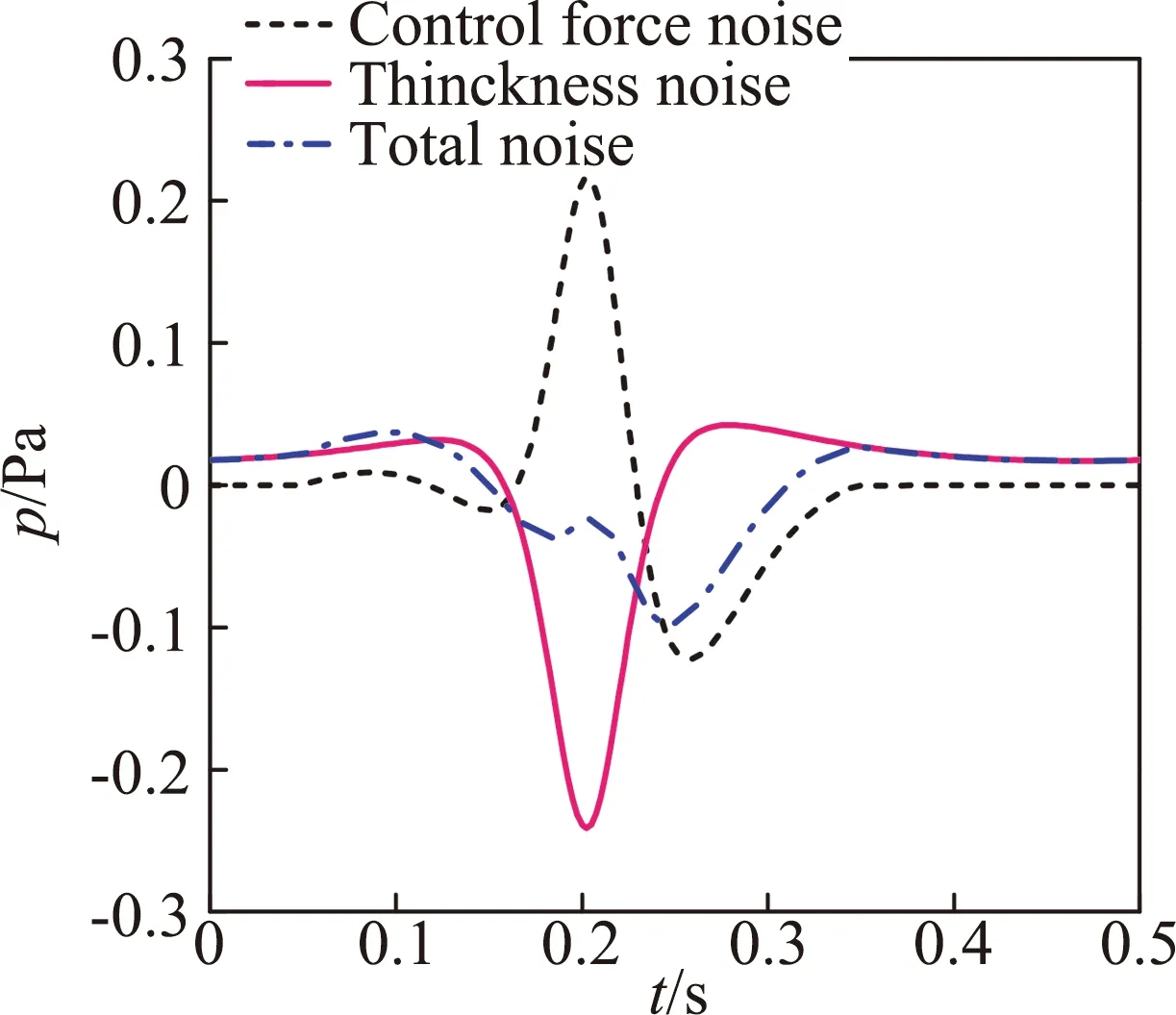
图2给出了基准观测点处旋翼气动噪声声压时间历程,该观测点位于桨盘面内,远场旋翼噪声主要由厚度噪声决定,载荷噪声占比很小。图3进一步对观测点处厚度噪声的波形构成进行了分析,旋翼厚度噪声主要由两部分构成,其中负压项由噪声方程中的速度导数项引起,该项决定了厚度噪声的主要波形特征,速度项产生了关于厚度噪声峰值对称的两个正峰值。
2.2 参数影响分析
图4和图5分别给出了悬停状态下不同展弦比和厚度时的旋翼厚度噪声声压时间历程。从图中可以看出,当展弦比增大时,桨叶弦长减小(桨叶半径不变),桨叶前后缘引起的扰动到达观测点的时间差变短,致使厚度噪声声压脉冲变宽,声压负峰值减小;当旋翼厚度增大时,相同速度下桨叶排开空气的体积增大,声压负峰值增大,脉冲变窄。但展弦比和厚度均对旋翼厚度噪声的相位(峰值的发生位置)无明显影响,这对于厚度噪声的控制尤为重要。
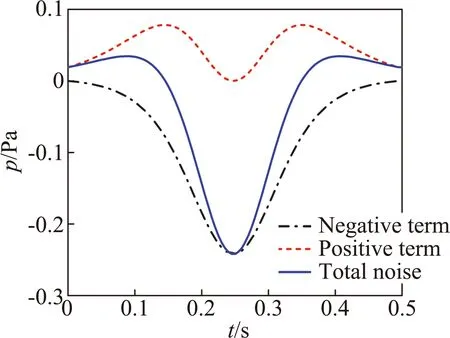
图3 观测点处厚度噪声声压时间历程
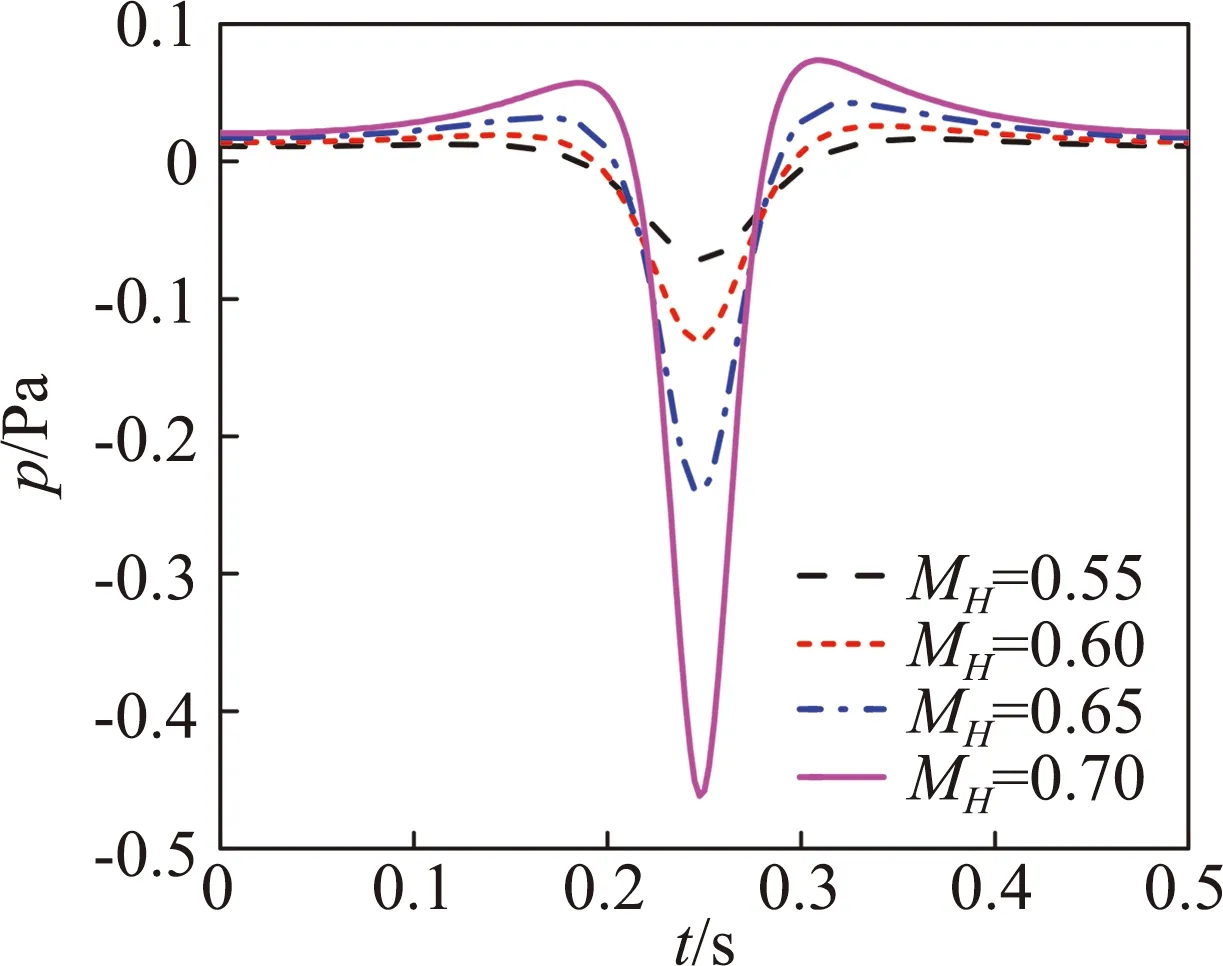
接下来研究桨尖马赫数对旋翼厚度噪声的影响。悬停状态下桨尖马赫数MH分别是0.55、0.60、0.65、0.70。图6给出了悬停状态下旋翼厚度噪声随悬停桨尖马赫数变化的示意图,当旋翼桨尖马赫数增加时,会使得桨叶排开空气的速度增加,旋翼厚度噪声负峰值会明显增大,脉冲变窄。
3 厚度噪声控制机理分析
3.1 桨尖控制力噪声特性
采用桨尖非定常控制力进行噪声控制时,远场任一观测点的噪声可以表示为:
fp′T+p′F=0
(5)
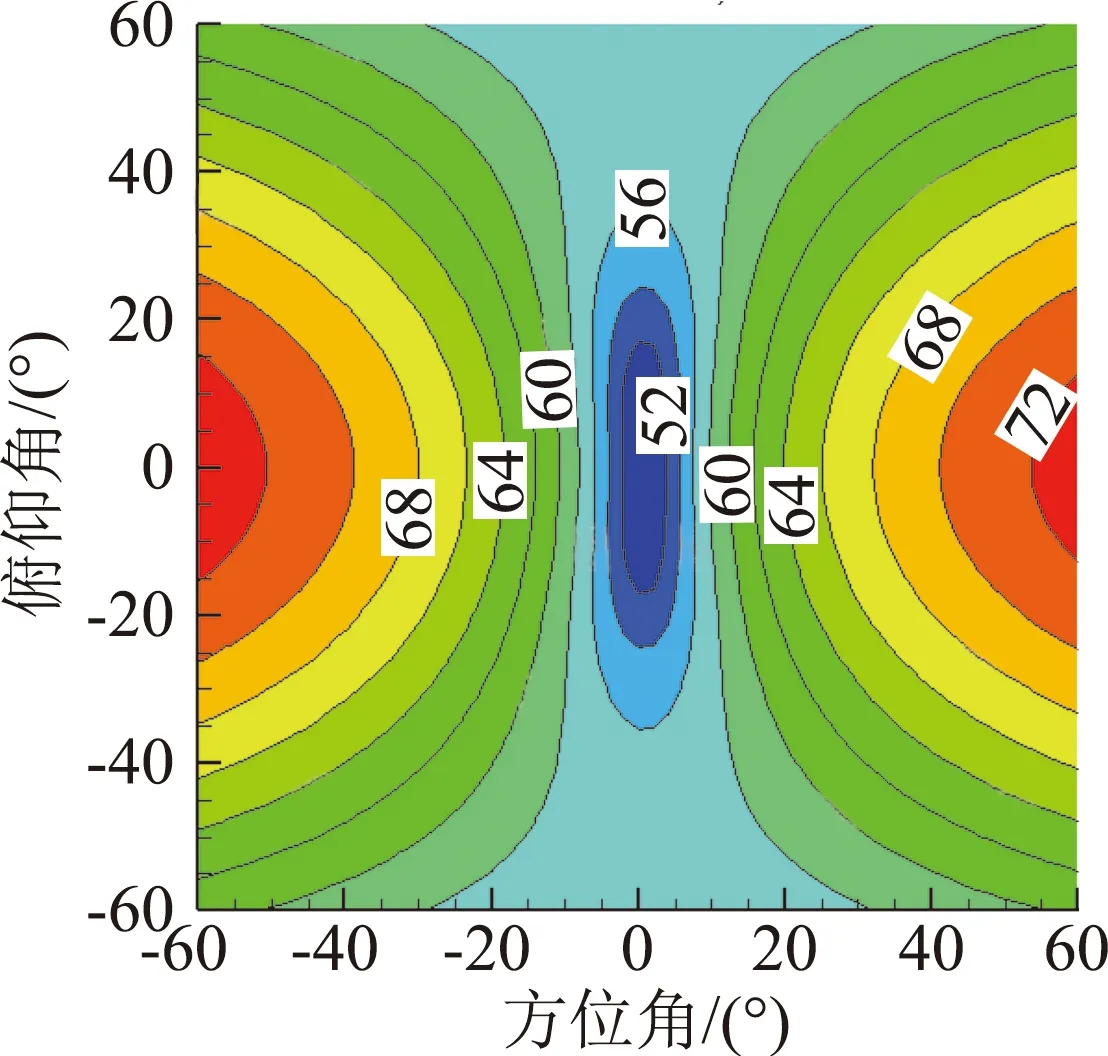
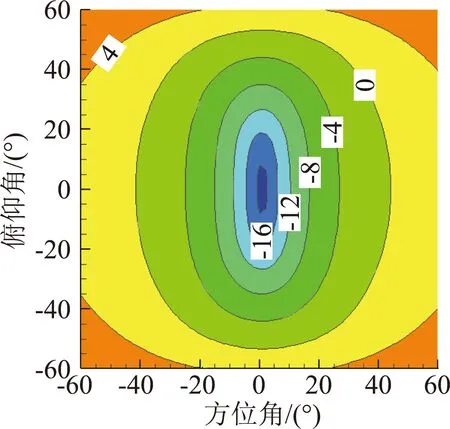
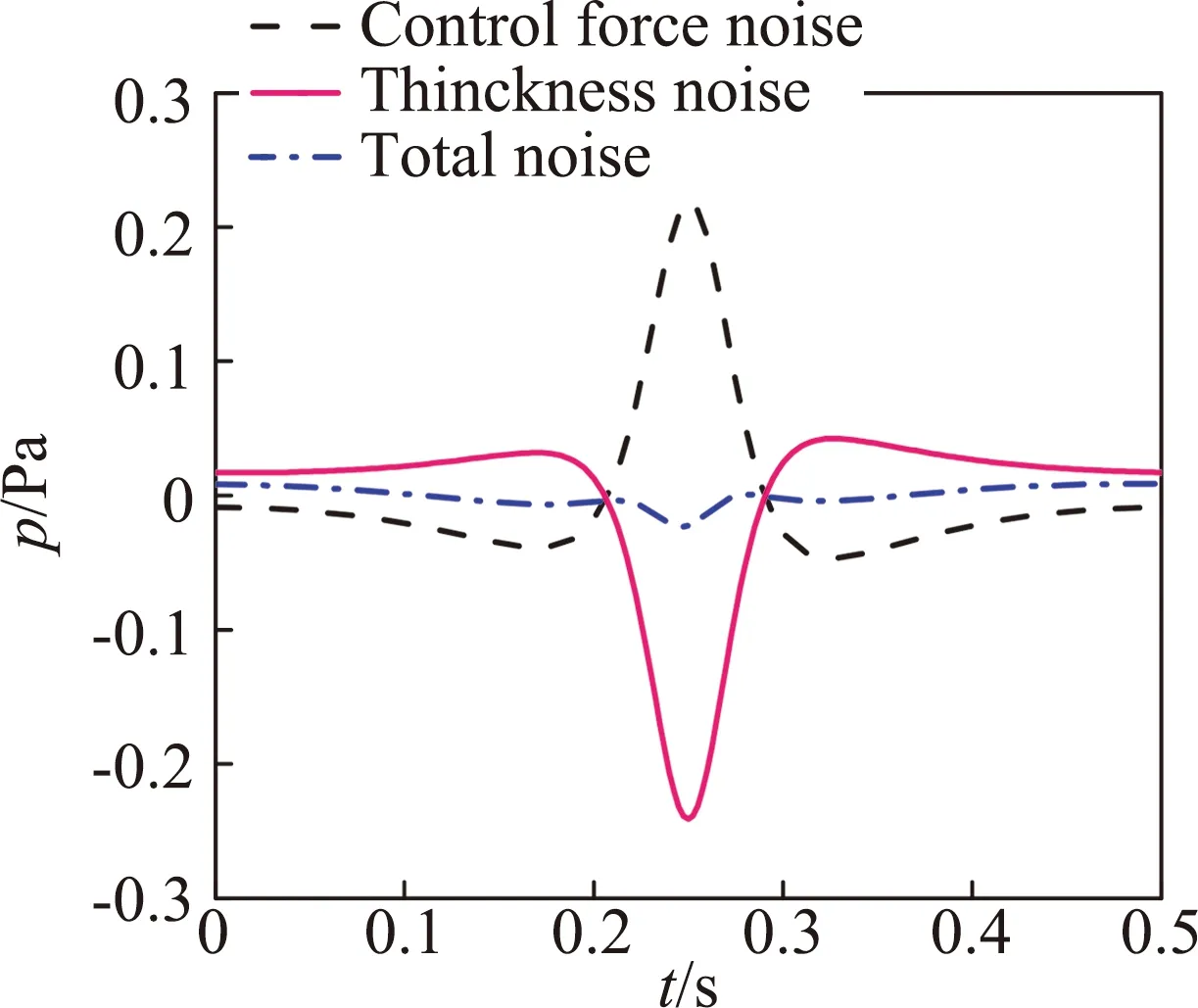
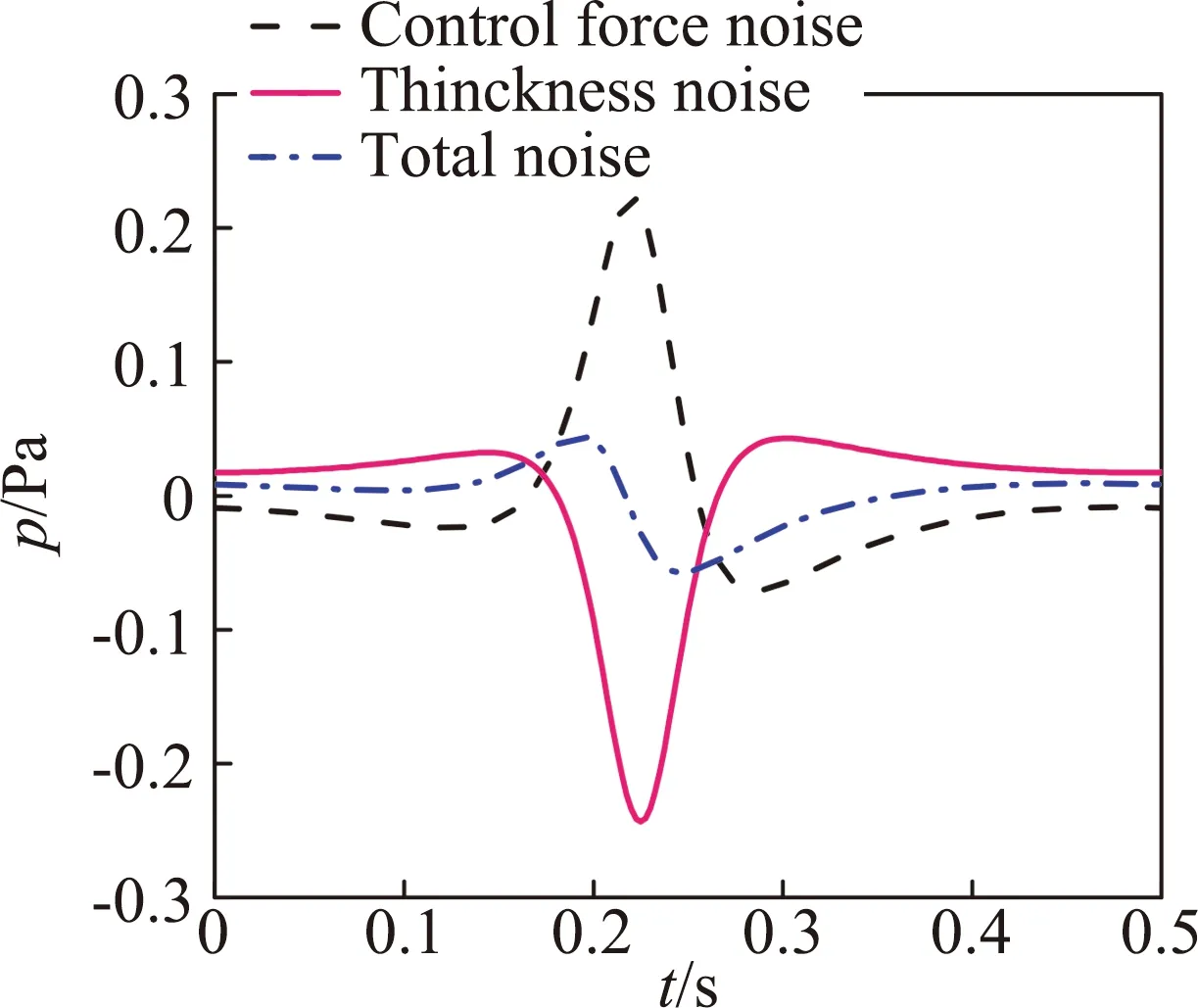
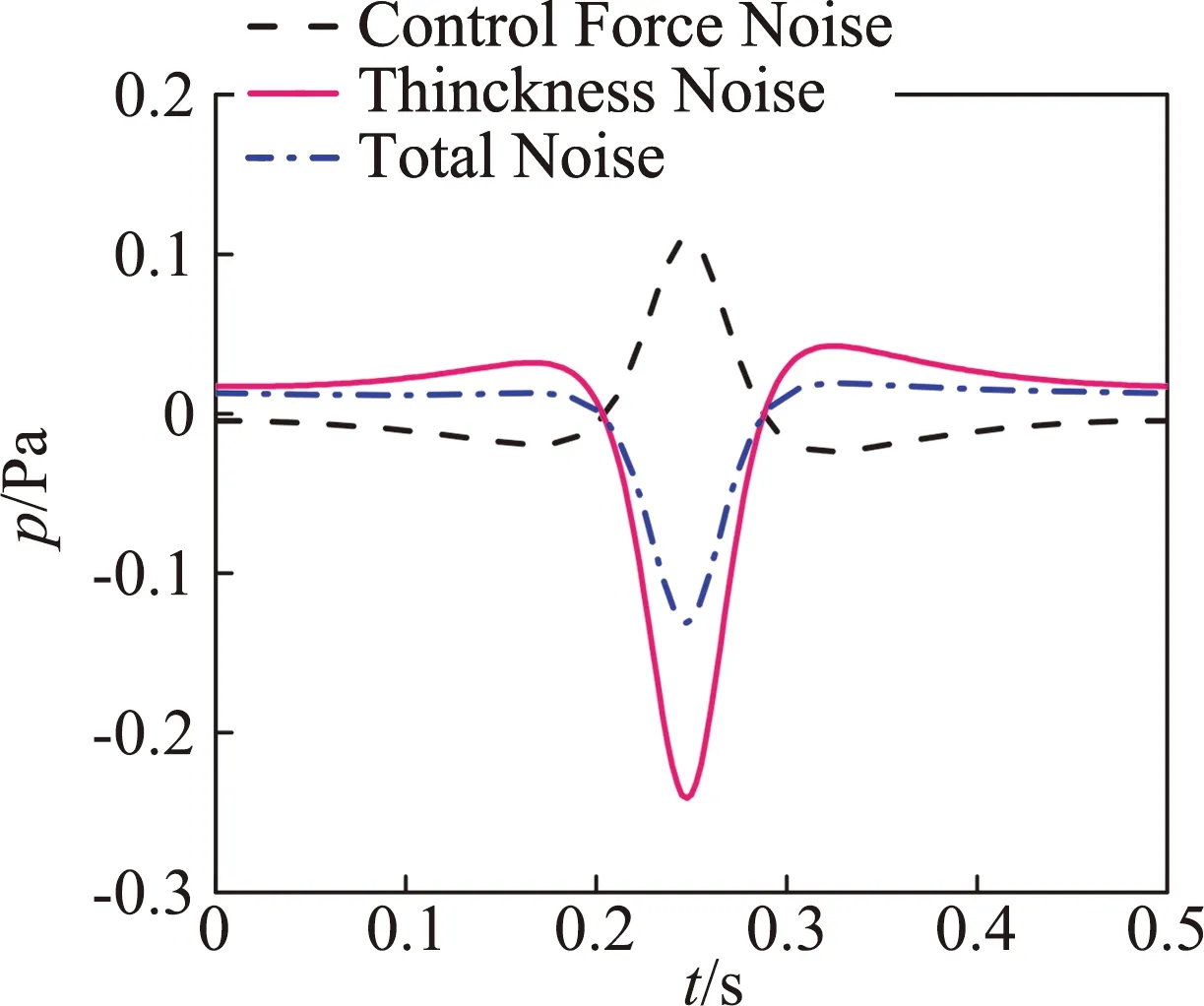
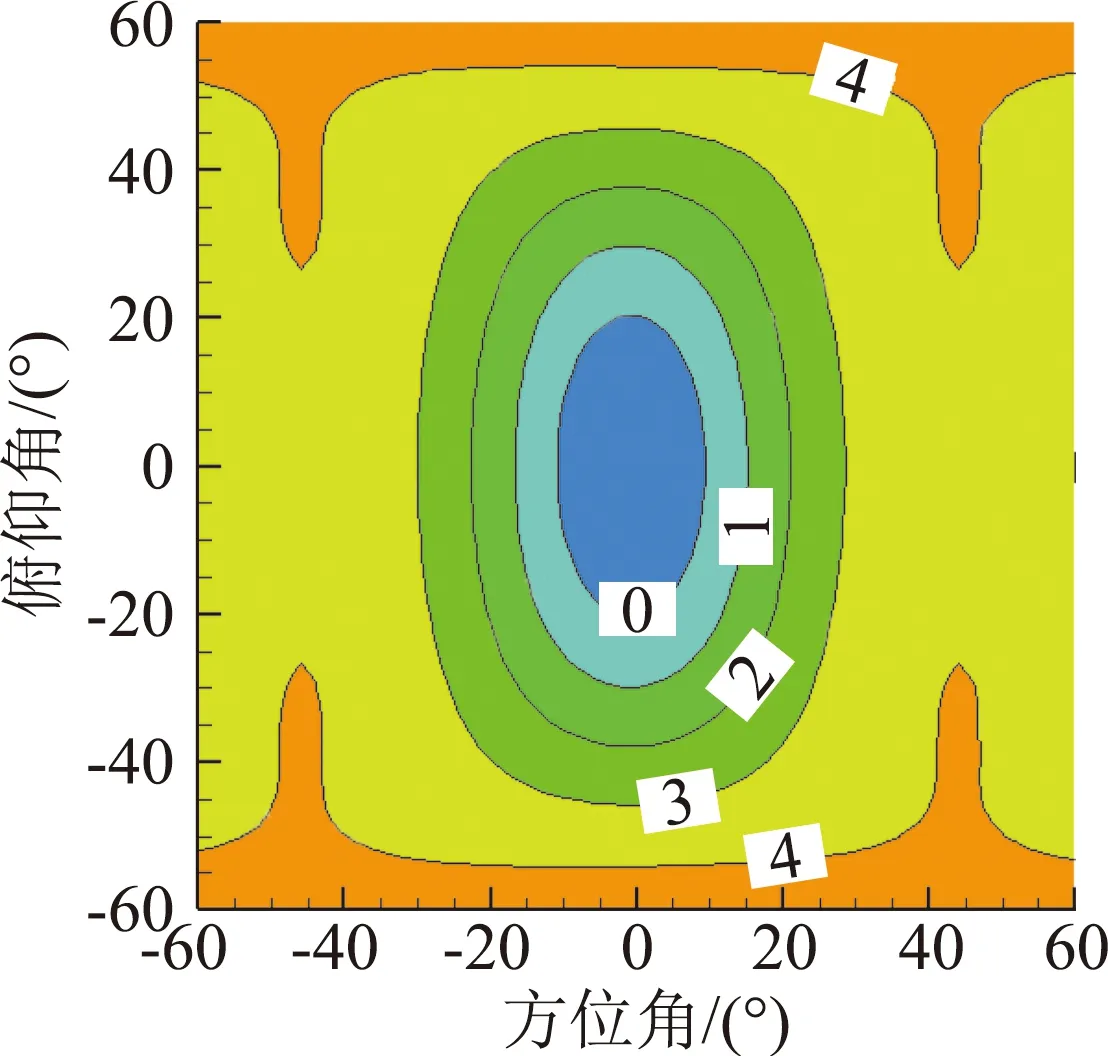
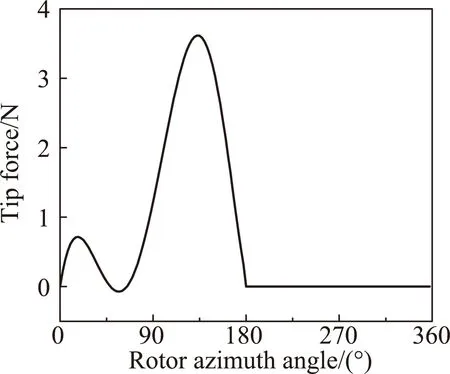
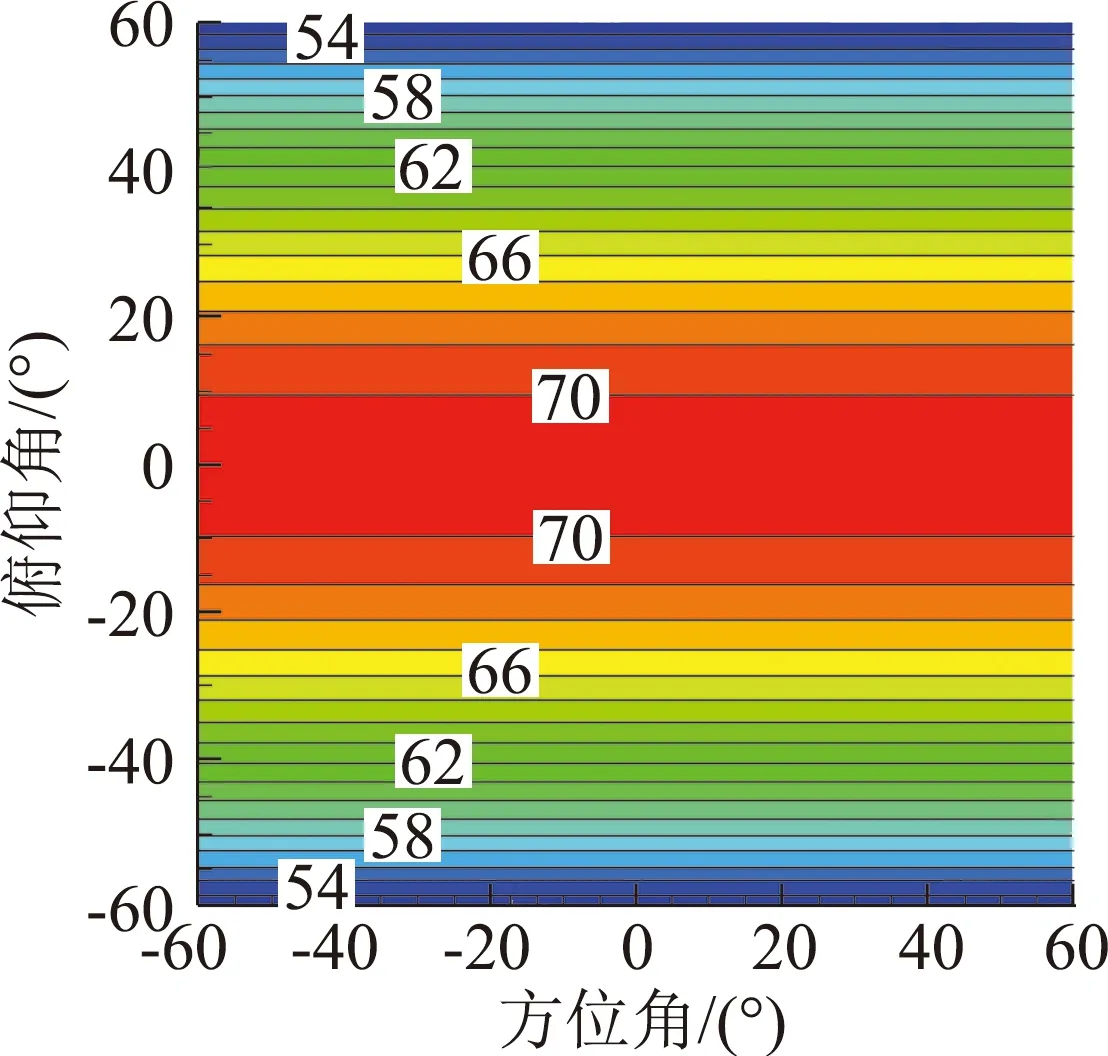
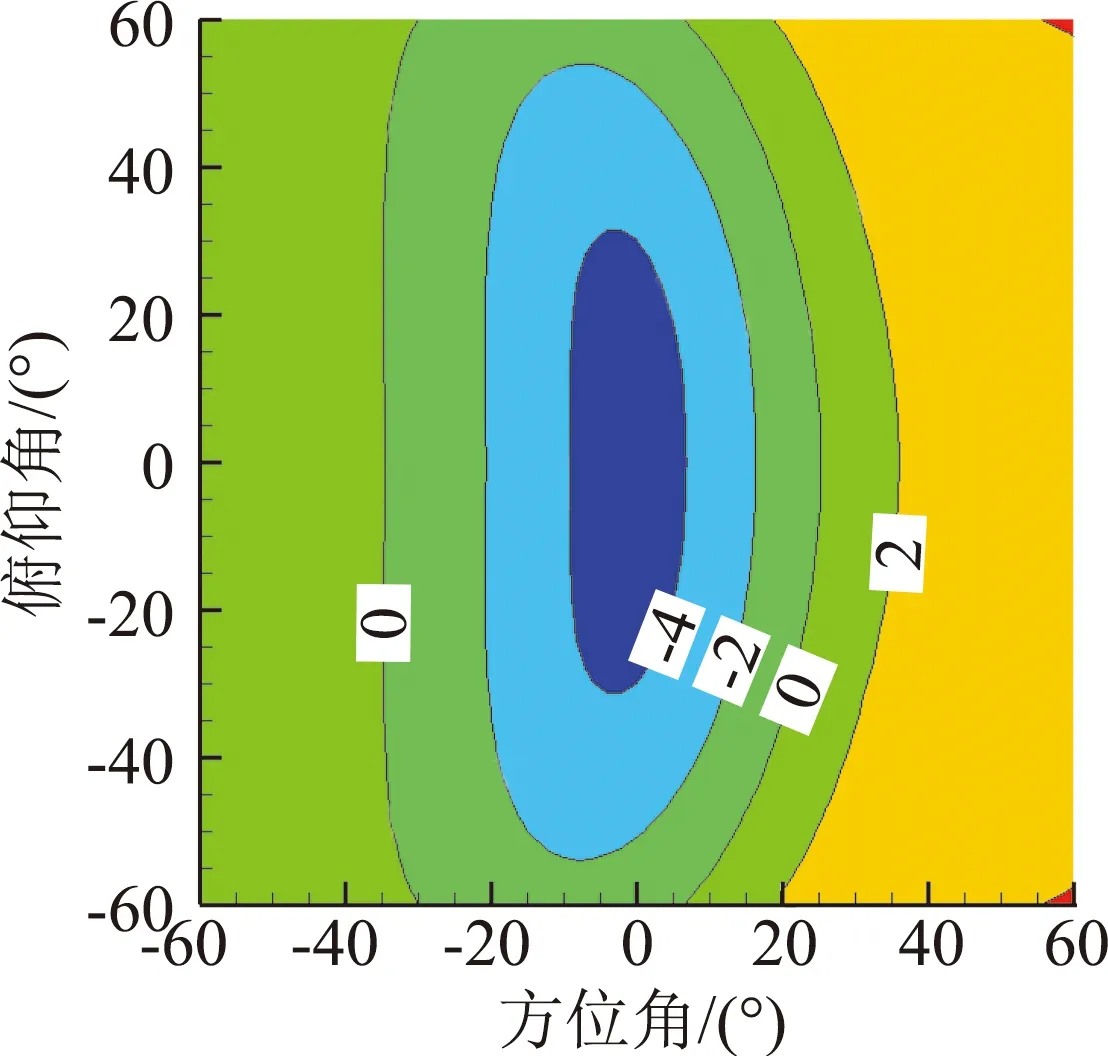
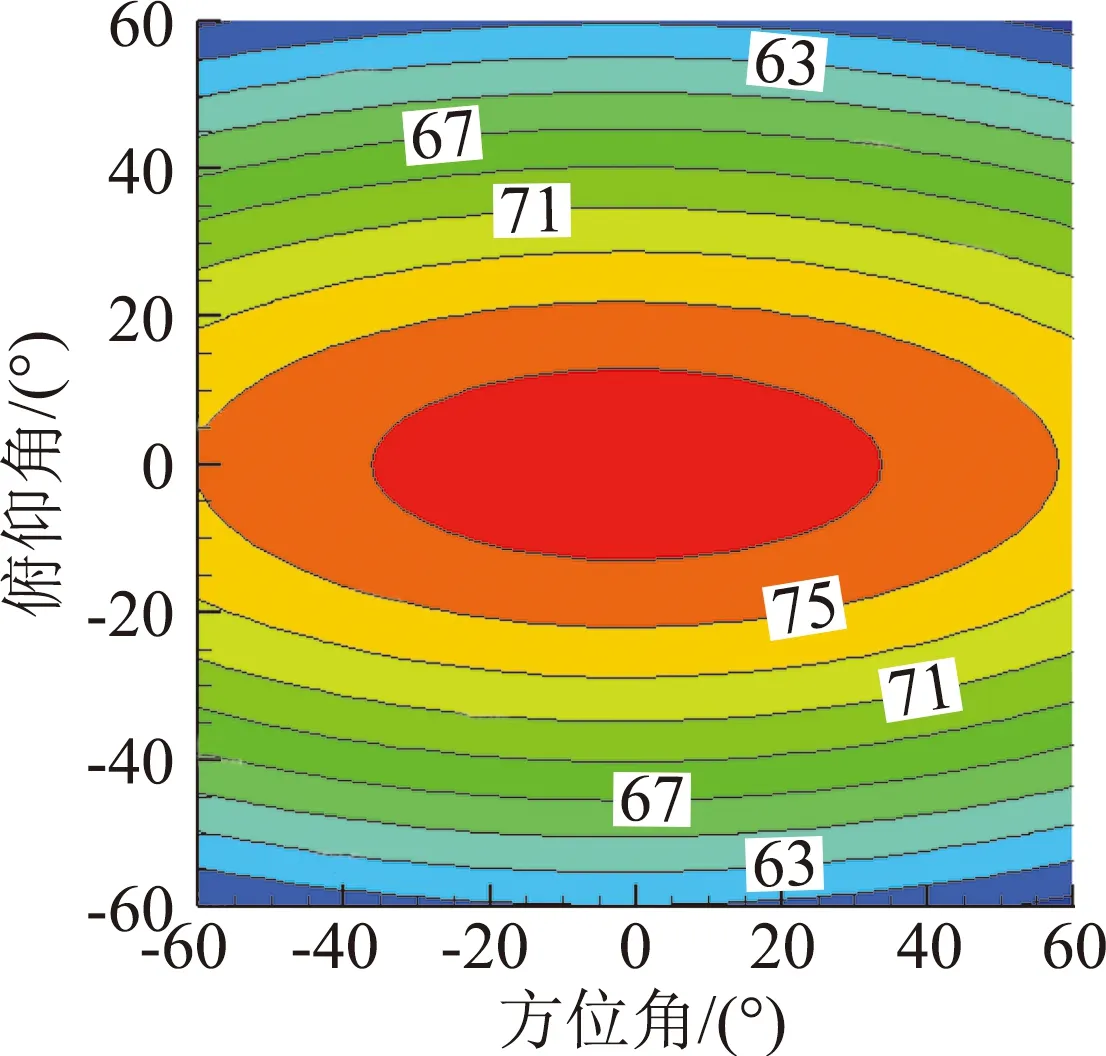
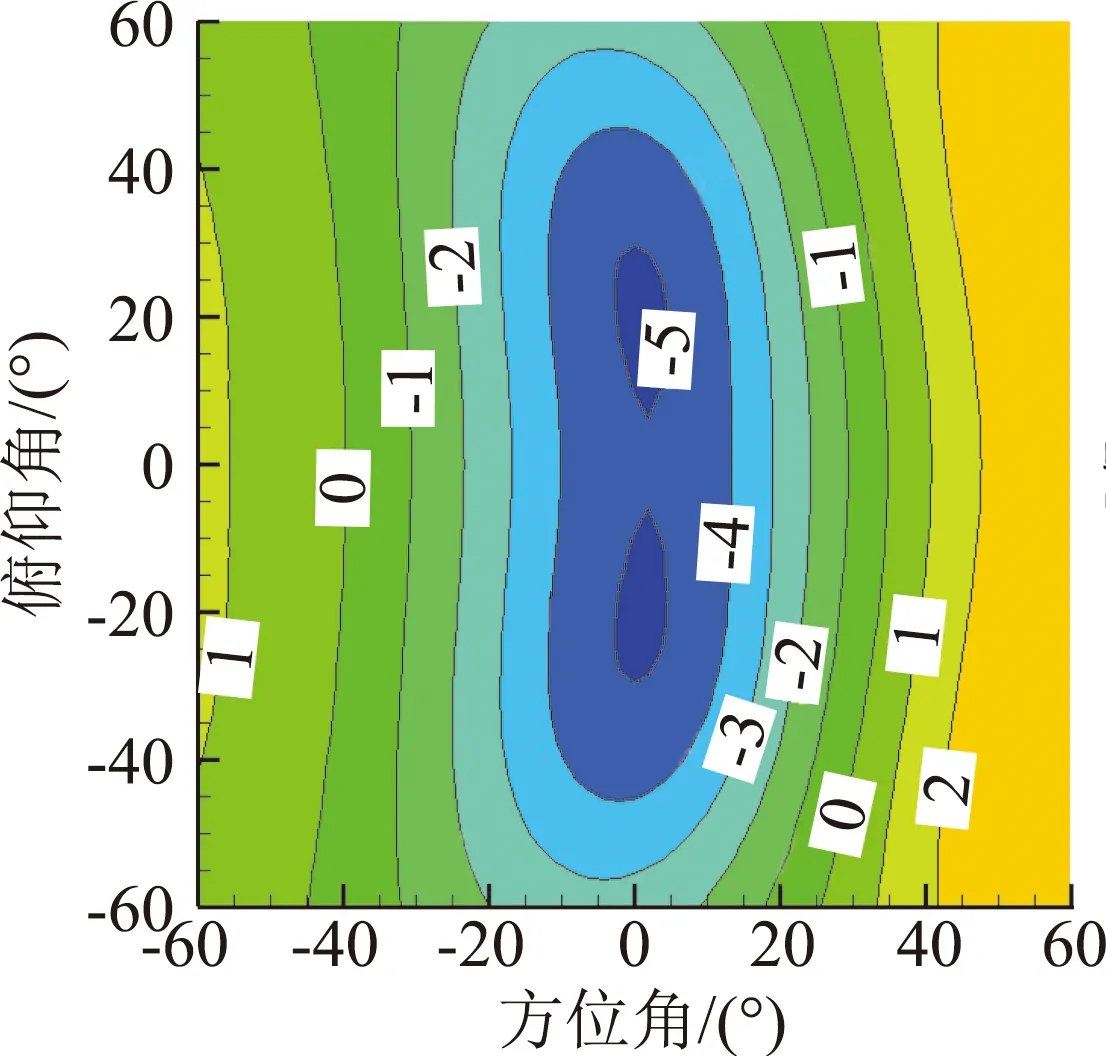
式中,f为抵消因子,f=1表示声压完全相消,0 为了获得非定常控制力的输入规律,本文采用文献[7]中推导出的旋翼单/偶极子噪声的简化解析表达式: 图4 不同展弦比时厚度噪声声压历程 图5 不同厚度时厚度噪声声压历程 图6 不同旋转桨尖马赫数的厚度噪声声压历程 (6) (7) 式中,f(MH,ψ)为解析函数,观测距离d=100R。 当抵消因子f=1时,将解析表达式带入式(5)可以得到桨尖控制力的控制规律如图7所示,控制力波形呈现类谐波函数的特点。因此,本文接下来研究了输入规律为谐波函数的桨尖控制力对旋翼厚度噪声的影响。控制力F的输入函数为: (8) 式中,Fn是控制力幅值,n为谐波频率,m为相位控制因子。 图7 控制力变化示意图 图8给出了输入规律为F=-4cosψ的非定常控制力产生的载荷噪声声压时间历程,声压波形主要由两项构成,控制力导数项引起的正声压决定了控制力噪声的主要特征,可以抵消厚度噪声的负声压;而控制力项引起了沿声压峰值对称的负声压波形,可以抵消厚度噪声的正声压,从而实现基准观测点处的声压对消。非定常控制力引起的载荷噪声主要沿力方向传播,且由控制力导数项决定,因此为了实现声压相消,非定常控制力在桨盘90°方位角处的变化率必须最大。 图8 观测点处控制力噪声声压时间历程 图9(a)、9(b)分别给出了添加桨尖控制力后目标观测区域内的总噪声声压级分布和声压级变化,声压级变化小于零的部分表示噪声降低区域。由图可见,添加桨尖阻力后,声场辐射特性发生了明显变化,旋翼前方区域的声压级明显降低,而两侧的声压级有所增加,且远场区域(-40°≤ψobs≤40°,-50°≤θobs≤50°)内的噪声声压级均明显减小,中心区域的声压级降低16 dB左右,部分区域声压级虽有所增加,但声压级较低,对总体声压级影响较小。接着,图10给出了添加非定常控制力后桨盘平面内三个观测点的声压时间历程,控制力不仅能使基准观测点的声压大部分相消,而且可以降低左右两侧观测点的噪声。 接下来分析控制力幅值对桨盘平面内旋翼厚度噪声的影响,图11分别给出了采用控制力幅值Fn为2N、4N、8N的1阶谐波控制力进行厚度噪声降噪时基准观测点处的声压时间历程。控制力幅值增加,控制力产生的正声压增加,基准观测点声压级降低,随着控制力幅值的进一步增大,会产生过大的正声压,反而使基准观测点声压级增大。此外,非定常控制力的输入还会引起功率消耗,因此在实际应用中需要选择合适的控制力幅值进行旋翼厚度噪声降噪。 为分析控制力频率对厚度噪声降噪的影响,图12给出了添加幅值Fn=2N,谐波频率n分别为1、2、3的控制力后基准观测点处的声压时间历程。图中可见,当谐波频率增加时,控制力产生的正声压增大,基准观测点的降噪效果变好,控制力频率的进一步增大则会使控制力产生的正声压过大,反而使声压级增大,这与控制力幅值的降噪效果一致。综合分析控制力幅值和频率分别对基准观测点处厚度噪声的降噪效果,可以发现当Fnn=4时总噪声大幅度减小,当Fnn>8时总噪声增加,这是因为当控制力在桨盘平面90°方位角处变化最快时,控制力噪声主要由控制力导数项的幅值Fnn决定。 为了更好地分析谐波频率对厚度噪声的影响,本文在控制力导数项幅值一定的前提下(即Fnn=4),分析了不同谐波频率对旋翼厚度噪声降噪区域面积的影响。引入降噪因子S用来表征不同输入规律的控制力对降噪区域面积的影响,如式(9)所示: (a)总噪声声压级 (b)声压级变化 (a)ψobs=-15° (b)ψobs=0° (c)ψobs=15° 图10 桨盘平面内不同观测点的噪声声压时间历程 Fig.10 Thickness noise pressure reduction using active tip force at different observer locations (a)Fn=2N (b)Fn=4N (c)Fn=8N 图11 不同控制力幅值的噪声声压时间历程 Fig.11 Thickness noise pressure reduction using different amplitudes of tip force at the target observer locations (9) 式中,S总为目标观测区域总面积,Δψobs、Δθobs分别为降噪区域的横、纵坐标差。 图13给出了分别采用2、3、4阶谐波控制力后,目标观测区域内的噪声声压级变化。可见,在桨尖添加输入规律为谐波函数的控制力均可有效降低基准观测点处的旋翼厚度噪声,谐波频率越大,达到声压相消所需的控制力幅值越小,控制力需用功率越小,但声压级降低幅度减小。对比图9可以看出,采用1阶谐波控制力进行厚度噪声降噪时,降噪因子S1=0.44,谐波频率增加时,降噪因子分别为S2=0.26,S3=0.21,S4=0.04,即降噪区域面积逐渐减小。因此,在采用桨尖非定常控制力进行旋翼厚度噪声降噪的实际应用中,需综合考虑控制力的需求功率以及降噪区域面积大小,可以采用多阶谐波叠加的形式实现功率消耗小的大范围降噪。 根据前面的计算结果可以发现,通过在桨叶端部添加非定常控制力可以实现远场观测区域内的厚度噪声降噪。图7中给出的控制力存在正、负的变化,正表示阻力,负表示推进力,然而在实际情况下,在旋翼上施加周期变化的推/阻力是不现实的,因此,本文采用阻力激励器的形式只产生正方向的阻力。在求解控制方程(5)时,为保证控制力始终为正(阻力),仅考虑方位角0°~180°区域内的控制力,其余方位角控制力为0,最终得到如图14所示控制规律的桨尖阻力,可以看出,桨尖阻力也具有在90°方位角处变化率最大的特点。 图15(a)给出了目标观测区域的厚度噪声声压级(dB)分布图,可以看出悬停状态下旋翼厚度噪声不随桨盘方位角变化,仅与俯仰角有关,桨盘面内噪声声压级最高,当观测点远离桨盘平面,噪声声压级降低,这也验证了旋翼厚度噪声主要沿桨盘面内传播的特性。施加图14所示的阻力激励后,目标观测区域内的声压级变化如图15(b)所示,声压级变化小于零的部分表示噪声降低区域。可见,旋翼前方区域(-30°≤ψobs≤20°,-50°≤θobs≤50°)内的噪声声压级均明显减小,中心区域的声压级降低5 dB左右,降噪因子SH=0.33。但左右两侧的声压级有所增加,这可能是因为0°和180°方位角处桨尖阻力突变引起的。研究中发现,阻力控制规律对厚度噪声的降噪影响很大,不合适的控制规律会减小降噪效果,因此本文后续将继续开展阻力控制规律的研究,通过优化设计,扩大桨尖阻力的降噪面积。图15(c)给出了基准观测点的声压时间历程,阻力激励器产生的控制源噪声基本可以抵消基准观测点处的厚度噪声。这表明本文通过阻力激励器添加的桨尖非定常控制力可以有效降低旋翼正前方区域内的旋翼厚度噪声,并且可以实际应用到直升机旋翼噪声的降噪中。 (a)n=1 (b)n=2 (c)n=3 图12 不同控制力谐波频率的噪声声压时间历程 Fig.12 Thickness noise pressure reduction using tip force with different harmonic frequencies at the target observer location (c)n=4, Fn=1N 图13 不同控制力谐波频率的旋翼厚度噪声降噪 Fig.13 Thickness noise SPL reduction using different harmonic frequencies of tip force at the target observer region in hover 图14 桨尖阻力的控制规律 由于直升机前飞状态下旋翼前行侧与后行侧桨叶的运动速度和气动环境不同,可能对噪声辐射特性产生影响,因此本节进一步分析了前飞状态下阻力激励控制的降噪有效性,计算状态为:μ=0.15,桨尖马赫数MH=0.65。 图16(a)给出了目标观测区域的旋翼厚度噪声声压级分布。与悬停状态不同的是,前飞状态下厚度噪声在方位角上具有明显的辐射方向性,这是因为由于多普勒效应的影响使得两侧的声压级降低,俯仰角方向上的变化规律与悬停一致,且厚度噪声沿水平方向的下降速度比沿竖直方向的下降速度慢。 图16(b)给出了阻力激励控制后噪声声压级变化。基准观测点处声压级降低6 dB,与悬停状态相比降低幅度增大。区域(-40°≤ψobs≤30°,-60°≤θobs≤60°)内的声压级均降低,可以计算出前飞状态下桨尖阻力的降噪因子SF=0.46,与悬停状态相比降噪面积增大,同样的桨尖阻力在前飞状态下的降噪面积更大,这是由于多普勒效应的影响,旋翼厚度噪声辐射沿方位角具有明显的方向性,左右两侧的厚度噪声声压级较低,致使同样的控制力能够降低更大区域面积的厚度噪声。图16(c)给出了基准观测点的声压时间历程,阻力激励器产生的控制源噪声基本可以抵消旋翼厚度噪声。前飞状态下的降噪结果表明本文发展的旋翼厚度噪声控制方法可以适用于不同飞行状态的直升机。 (a)厚度噪声声压级分布 (b)声压级变化 (c)基准观测点声压时间历程 图15 悬停状态下阻力激励器降噪效果 Fig.15 Thickness noise SPL reduction through tip force at the target region in hover (a)厚度噪声声压级分布 (b)声压级变化 (c)基准观测点声压时间历程 图16 前飞状态下阻力激励器降噪效果 Fig.16 Thicknessnoise SPL reduction through tip force at the target region in flight 在旋翼厚度噪声的实际应用中,采用阻力激励器降噪时需要考虑功率消耗,对于本文采用的AH-1/OLS旋翼,拉力系数约为0.005,根据升力公式T=ρΩ2R2πR2CT/2,可以估算出桨叶升力约为431.3 N,而桨尖阻力幅值最大为4 N(升力的1%),且阻力激励器只在一定方位角范围内工作,因此阻力激励器产生的额外功率消耗很小。 本文基于声压相消原理采用阻力激励建立了旋翼厚度噪声的控制方法,通过数值模拟进行了旋翼厚度噪声的控制机理和参数影响研究,得出结论如下: 1)对于直升机旋翼,桨叶展弦比减小、厚度增大或桨尖马赫数MH增大时,旋翼厚度噪声声压负峰值均增大,且旋翼厚度噪声主要沿桨盘平面传播; 2)在桨尖施加平面内控制力,在远场产生的声压波形中控制力项和控制力导数项可以分别抵消厚度噪声的声压波形,使得旋翼前方区域内的噪声降低,并且控制力在90°方位角处变化率最大; 3)控制力幅值或频率增大均可增加控制力噪声,当基准观测点降噪效果一定时,控制力谐波频率减小,降噪区域范围增大,但所需的控制力幅值较小,因此在应用中可采用多阶谐波叠加的形式实现厚度噪声降噪; 4)在桨叶外端布置阻力激励器可以实现桨尖非定常控制力的添加,且功率消耗低;悬停及前飞条件下的算例结果表明,阻力激励控制可以降低旋翼正前方区域的厚度噪声,且适用于不同飞行状态的旋翼厚度噪声降噪;前飞时由于厚度噪声辐射特性的不同,阻力激励降噪效果更好。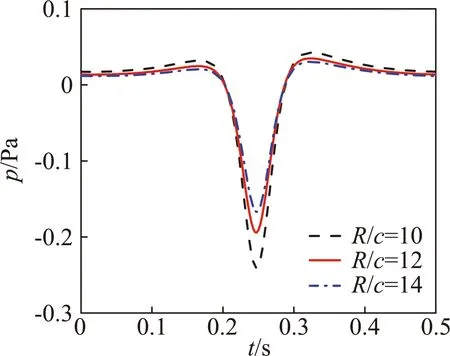

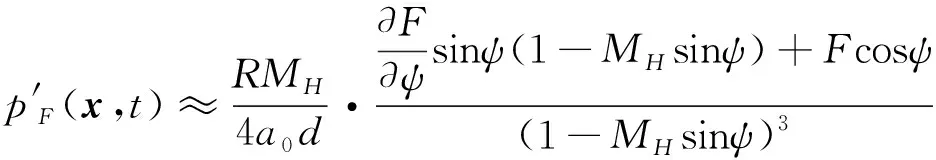

3.2 控制力幅值
3.3 控制力频率

4 基于阻力激励控制的旋翼降噪分析
4.1 悬停状态

4.2 前飞状态

5 结 论
