牛顿环等厚干涉与迈克尔孙等倾干涉的比较

刘敏敏

(武汉工程大学光电信息与能源工程学院,数理学院 湖北 武汉 430205)

在大学物理光的干涉教学中，牛顿环等厚干涉与迈克尔孙等倾干涉是教学中很重要的内容．由于干涉条纹的相似性，学生在学习时往往很容易把牛顿环等厚干涉与迈克尔孙等倾干涉混淆起来[1～4]，本文着重分析和总结了牛顿环等厚干涉与迈克尔孙等倾干涉的特点、联系和区别，以供学习参考．

1 薄膜干涉

如图1所示，一折射率为n的透明薄膜，处于上下折射率分别为n′和n″的介质中，膜厚为d，从面光源(扩大光源)上S点发出的真空波长为的光线0以入射角i射到膜上A点后，分成两部分，即反射光和折射光，到薄膜中在膜下表面B处又反射之后经C处折射到介质n′中，即2光．显然，1和2光是平行的，经透镜L会聚后在P点．因为，1和2光是来自同一入射光，因此1和2光的振动方向相同，频率相同，在P点的位相差固定，所以二者产生干涉．一束光经薄膜二表面反射和折射分开后，再相遇而产生的干涉称为薄膜干涉．又因1和2各占入射光0的一部分，所以此种干涉称为分振幅干涉．

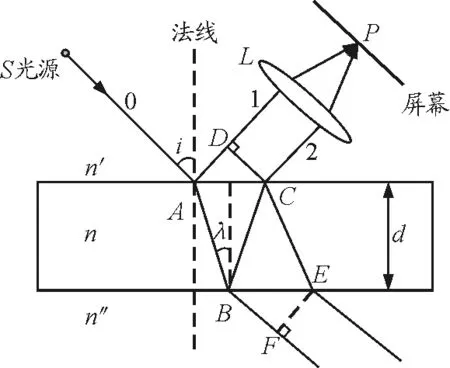
图1 薄膜干涉示意图

光束1,2 的光程差为

(1)

其中，k为条纹的级次．按照产生干涉的原因不同，薄膜干涉可分类为:

(1)等厚干涉.在薄膜干涉中光入射角i不变，即为常数时，干涉随厚度的变化而形成不同级次的条纹，在同一厚度下形成同一级次的条纹，称为等厚干涉．

(2)等倾干涉.在薄膜干涉中薄膜厚度d不变，即为常量时，干涉随倾角的不同而变化形成不同级次的条纹，在同一倾角下形成同一级次的条纹，称为等倾干涉．

2 牛顿环等厚干涉和迈克尔孙等倾干涉

2.1 牛顿环等厚干涉

牛顿环光路以及干涉条纹示意图如图2所示.

图2 牛顿环光路以及干涉条纹示意图

其中R为牛顿环平凸镜的曲率半径，平行光垂直入射，入射角i=0, 空气膜折射率n=1，代入式(1)，牛顿环的光程差和产生明暗纹的条件为

(2)

可得明条纹级次k满足如下条件，其中dmax为空气膜的最大厚度

(3)

事实上，当空气膜的厚度远大于入射光的波长时干涉现象将会不明显甚至消失，如在牛顿环实验中我们可以观察到此现象，在牛顿环的平凸镜与平板玻璃接触点附近，干涉现象明显，离接触点较远的地方，干涉现象变得不明显，用肉眼观察时，则看不到干涉的细小条纹，这也正是光的干涉在障碍物尺寸与光波波长相比拟的条件下产生的一种体现．另外，干涉明暗条纹的半径可表示为

(4)

从式(4)可以看出，随着条纹级次k的增加，干涉条纹的半径增加，但是由于条纹表达式不是等差数列，即相邻两条纹间距不相等，以明条纹为例，则两相邻的明条纹间距为

(5)

式(5)表明相邻两条纹的间距Δr是级次k的单调递减函数，级次k越大，间距Δr越小，级次k越小，间距r越大，由于里环的级次k小，外环的级次k大，因此整体条纹为以平凸镜和平板玻璃的接触点为中心，里环稀疏，外环密集的明暗相间的同心圆环．

2.2 迈克尔孙等倾干涉

迈克尔孙等倾干涉光路以及干涉条纹示意图如图3所示，d为等效空气膜的厚度，f为观察干涉条纹透镜的焦距，迈克尔孙等倾干涉的光程差与明暗纹条件为

Δ=2dcosi=

(6)

图3 迈克耳孙干涉仪光路以及干涉条纹示意图

当入射角为零度垂直入射时，对应着干涉条纹的中心，随着入射角度增加，条纹以中心为圆心向外展开．由式(6)可知中心的条纹级次最高，随着入射角度的增加，光程差随之递减，条纹向外展开时，条纹级次越来越低．

以明条纹为例，则可以得到入射角i随级次k的微分

(7)

可以看到随着入射角度的增加，相邻两明条纹角度间距减小，即以干涉条纹中心为参考，干涉条纹里环稀疏，外环密集．

由明条纹条件可得

(8)

可得条纹级次的取值范围为

(9)

等效空气膜的厚度d决定了条纹的级次的最大值，最高级次对应零度入射角，即垂直入射的情形．

由式(8)可得

(10)

从光路以及干涉条纹示意图可以得条纹半径

(11)

故级次k越大，条纹rk半径越小．而且，由式(11)可得两相邻的明条纹间距为

Δr=rk+1-rk=

(12)

式(12)表明两相邻的明条纹间距Δr是级次k的单调递增函数，可以看出级次k越大，间距Δr越大，级次k越小，间距Δr越小，由于里环干涉条纹级次k大，外环干涉条纹级次k小，因此，整体干涉条纹为里环稀疏，外环密集的明暗相间的同心圆环．

3 牛顿环等厚干涉与迈克尔孙等倾干涉的比较

牛顿环等厚干涉与迈克尔孙等倾干涉条纹，都是明暗间隔的圆环，从干涉圆环中心往外，干涉条纹越来越密．然而，虽然牛顿环等厚干涉条纹和迈克尔孙等倾干涉条纹具有相似的形状，但两种干涉却具有不同的本质，两者的联系与区别主要可分为以下几点：

第一，牛顿环等厚干涉的空气膜的厚度是变化的，迈克尔孙干涉仪的等效空气膜是厚度相等的．不能简单地从字面上理解等厚干涉为“厚度不变”，理解等倾干涉为“倾角不变”．

第二，产生牛顿环等厚干涉的入射光与等倾干涉的入射光线有所不同．在牛顿环等厚干涉中，入射光线是经扩展光源发出的平行光线，这些光线是垂直照射到牛顿环平凸透镜的上表面后进入空气膜，在介质( 空气) 相同厚度位置形成同一级干涉条纹． 而在迈克尔孙等倾干涉中，照射到空气薄膜上的是经面光源发出的具有不同倾角的非平行光线，其中具有相同倾角的入射光线产生同一级次干涉条纹．

第三，两种干涉的不同还体现在干涉条纹的级次上．牛顿环的干涉级次从条纹中心由内向外依次增加的，越往外，光程差越大，干涉级也越来越高．对于空气膜牛顿环，牛顿环干涉图形中心对应最低级次条纹．而在迈克尔孙等倾干涉中，从中心往外，对应的入射角角度的增加，光程差是逐渐减小的，干涉级次依次降低，中心对应最高级次的条纹，与牛顿环中的情形正好相反．对于等倾干涉图样的中心，光程差为2d，不一定是明纹或暗纹，而牛顿环空气膜中心厚度为零时则是暗斑．

第四，改变中间空气层厚度时，干涉条纹的移动规律不同． 在牛顿环等厚干涉中，通过逐渐增加中间空气层厚度，观察干涉条纹的移动，其干涉条纹是往中心收缩的；当减小薄膜厚度时，中心级次较低的干涉条纹向外冒出．而在迈克尔孙等倾干涉中，逐渐增加空气层厚度，由式(9) 可知，级次随之增加，等倾干涉条纹一个个从中心冒出并往外移动；反之减小空气膜的厚度时外围级次较低的条纹向中心收缩．在条纹的移动随空气膜厚度的增减的变化上，牛顿环等厚干涉和迈克尔孙等倾干涉情况是相反的．

第五，由明条纹半径公式(4)与(11)可知牛顿环和迈克尔孙等倾干涉的条纹半径表达式不一样，由两相邻明条纹间距公式(5)和公式(12)可知，牛顿环相邻两干涉明条纹的间距与迈克尔孙等倾干涉两相邻明条纹的间距的表达式也不一样，影响它们的具体因素实际上是不一样的．虽然条纹看上去非常相似，但是它们的本质不同．

第六，迈克尔孙干涉仪通过调节，也可以实现等厚干涉，只是其干涉条纹不再是同心的明暗相间的圆环，而是近似平行的弧形，或者经细致调节后得到的平行的等间距的明暗相间的干涉条纹．

总之，对于牛顿环等厚干涉和迈克尔孙干涉仪等倾干涉，理清它们的本质规律有利于学生在学习时理解和掌握它们．在教学的过程中，注意比较它们的异同之处，有助于帮助学生理解和掌握此两处知识点，并且进一步理解光的干涉性质以及波动本性．