基于信息熵属性约简的相似重复记录检测方法∗
2019-12-27陈彦萍洪明杰杨小宝
陈彦萍 洪明杰 杨小宝
(西安邮电大学 西安 710121)
1 引言
随着互联网信息技术的不断发展,数据信息的潜在价值逐渐被重视,对企业的生产决策、市场销售、经济效益、竞争力提升等都有着重要作用[1]。然而由于数据信息共享、数据迁移、来自同一实体的不同表达、输入拼写错误或是受数据来源不同等原因导致了相似重复数据的存在,相似重复数据可能会影响程序运行速度,同时也会占用更多存储空间和传输带宽和时间,消耗更多的网络流量,更不利于后续的数据挖掘工作,精准可靠的高质量数据是数据挖掘的前提,是进一步提取数据潜在价值的基础,提高数据质量[2]对于优化资源利用、降低数据管理成本也有着重要意义。
相似重复记录检测是数据清洗中的关键步骤,是判断该记录是否表示的是现实世界中的同一实体。传统的检测相似记录的方法主要是对记录的相似度匹配:“排序 & 合并”[3~4]比较次数较多时间复杂度较高,邻近记录排序[5]算法(Sorted Neighbor⁃hood Method,SMN)的滑动窗口大小设定对检测效率影响很大,编辑距离算法[6~7]对字符拼写错误及字符缩写检测检测率比较低,还有依据记录内码序值[8]、基于tokens值[9]的相似检测算法也都致力于减少记录比较次数。随着数据量的增加,数据来源的不同,数据结构也不一样,传统方法面临新的难题,聚类算法[10~11]应用对于相似重复检测有着显著效果。文献[12~14]根据关键属性或属性权重对数据集先进行分组聚类处理,再进行相似检测,在处理大量数据中提高了检测效率,文献[14]针对高维数据用R-树进行索引,应该聚类思想完成相似记录的检测,文献[15~16]分别对重要属性和非重要属性进行二次判断,依据属性进行分组,并在记录检测时采用提取记录字段相似度的特征向量的方法完成对相似记录检测。国内外的研究学者对相似重复记录检测已经有了广泛的研究,提出了较多的方法,其中聚类分组思想是解决海量数据的相似重复检测的有效途径,但大数据时代数据的3V(Velocity、Variety、Volume)特点,如何提高检测的效率和精度?本文使用K-modes算法进行聚类分组方法,依据信息熵值来确定属性权重并对属性维度进行约简,在聚类后的数据集中选择性权重较大的字段逐项进行比较,避免整条记录相似参与匹配耗费时间,提高了检测效率。
2 相关工作

图1 重复检测的流程图
如图1所示,一般对于重复检测主要有两大阶段:数据预处理和相似重复记录检测。这两大阶段处理和检测方法多种多样。预处理阶段是检测过程的基础,好的预处理方法对于检测结果影响至关重要。
相似重复记录检测是在数据集中识别出类似记录的过程,而聚类算法是将数据集相似数据进行分类的过程,簇内的对象保持一定相似性,簇间对象相异,所以运用聚类的思想可以有效帮助找出每个簇内相似重复率,在检测大量数的记相似性上具有良好的效果。
2.1 K-modes聚类算法
K-modes[17]是对 K-means算法的扩展,保留了K-means算法效率的同时将K-means的应用扩大到离散数据,K-modes算法采用相异度来度量记录之间相关程度,使用一个簇类的每个属性出现频率最大的那个属性值作为代表簇的属性值来更新modes。
设 S=(U,A)是一个信息分类系统,U={x1,x2,…,xn},A={a1,a2,…,an}, xi,xj∈ U(1 ≤ i,j≤ n), xi和xj分 别 被 A 描 述 为 xi=(f(xi,a1),f(xi,a2),…f(xi, am)) 和 xj=(f(xj, a1), f(xj, a2), …f(xj, am)),xi和xj的距离定义为其中:

W是 n×k的{0,1}矩阵,n表示对象个数,k表示聚类个数,wil=1表示第i个对象被划分到第l类的中心,Z={z1,z2,…zk},zl(1≤l≤k)是第 l类的中心。
在约束条件(1)~(3)下达到极小化,K-modes聚类算法描述如下:
Step1:从数据集中随机选择k个对象作为初始聚类中心,k为聚类个数;
Step2:应用简单匹配算法计算每个对象到中心的距离,并分配到离它最近的类中;
Step3:基于频率重新计算各类的聚类中心;
Step4:重复Step3,Step4过程,直到目标函数F不再发生变化为止。

图2 K-modes聚类算法流程图
代码描述如下:
Radom(K)
for(int i=0;i<num;i++)
{
Int dis,mindis=0;
mindis=Distance(data[i],center[0]);
for(int j=0;i<k;j++)
{
dis=Distance(data[i],center[j]);
if(dis<mindis)
{
mindis=dis;
}
BeCluster(data[i]);
}
If(UpdataCenter)
{
for(int i=0;i<num;i++)
{
Int dis,mindis=0;
mindis=Distance(data[i],center[0]);
for(int j=0;i<k;j++)
{
dis=Distance(data[i],center[j]);
if(dis<mindis)
{
mindis=dis;
}
BeCluster(data[i]);
}
}
else
return Cluster;
2.2 信息熵
“熵”(entropy)最早是由鲁道夫·克劳修斯(Ru⁃dolf Clausius)于1854年提出的概念,其物理意义是体系混乱程度的度量,熵就越大则该体系越均衡。1948年克劳德·艾尔伍德·香农(Claude Elwood Shannon)提出了“信息熵”的概念,用来描述信源的不确定度,第一次用数学语言阐明了概率与信息冗余度的关系,解决了信息的量化问题。
假设离散型随机变量X(信源)的取值集合A={a1, a1, … aq},对应的概率预测 pi=P[X=ai],则义为

即信源的所提供的的信息量,一般以2为底,单位比特(bit)。
3 信息熵的属性权重计算和维度约简
对于一些包含多个属性字段多元数据,不同属性的提供的信息量不同,重要程度不同,需要确定这些属性的重要程度,从属性集合中去除某些非重要属性,实现属性维度的约简。
3.1 熵值计算属性权重
属性重要程度即为属性权重,目前权重确定方式分为主观赋权、客观赋权和主客观组合赋权三种方式。主观赋权依据专家经验来进行赋权,主观意愿较强,信息不能准确量化,客观赋权有充分的数理根据,具有较好的规范性。这里考虑到数据属性之间都有着复杂的联系,采用客观赋权的熵值法来计算各个属性的权重。
在聚类的簇中,可以将数据看做是n×m的矩阵,n表示簇类中的数据个数,m表示属性个数,各字段属性熵值可用以下方法来确定。
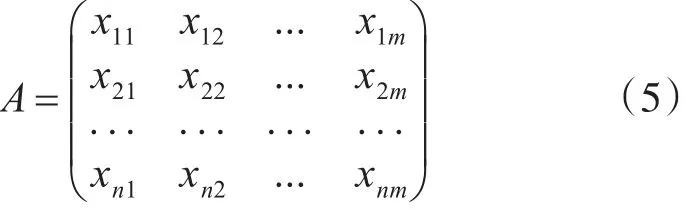
1)设某多维数据集A有m维属性n条数据,xnm表示m属性下第n条数据的值,可构建属性值的决策矩阵:
2)数据标准化处理,为了使不同量纲的数据具有可比性,对数据压缩到[0,1]区间上,每列所有数据和为 1,即,计算第i条数据的j属性所占的比重:

其中xij为属性值,Mij表示属性值比重。
3)第j维属性的熵值:
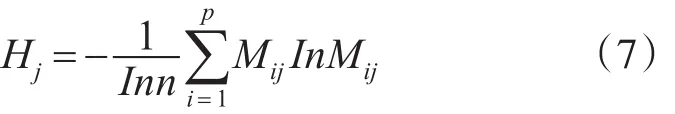
4)易得 0≤Hj≤1,若 Mij均相等,那 Hj=1,不易区分各属性优劣程度,所以定义区分度Fj=1-Hj,当属性值分布较为均匀时,熵值Hj越大,区分度Fj越小,该属性区分能力越弱,聚类作用也就较弱,反之亦然,所以Fj越大时,则该属性就越重要。
5)计算第j维属权重:
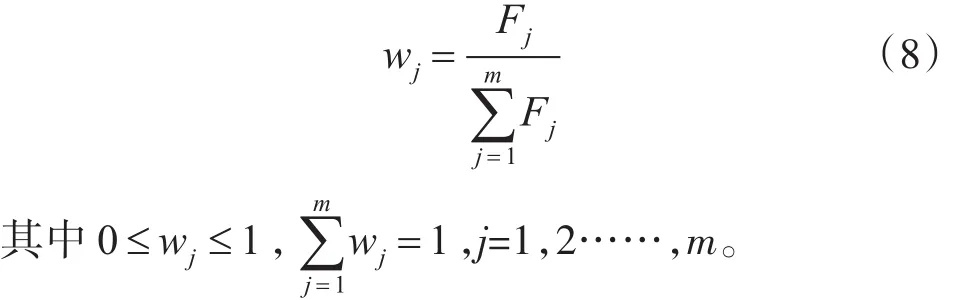
3.2 属性维度约简
应用熵值法确定属性权重并约简非重要属性。
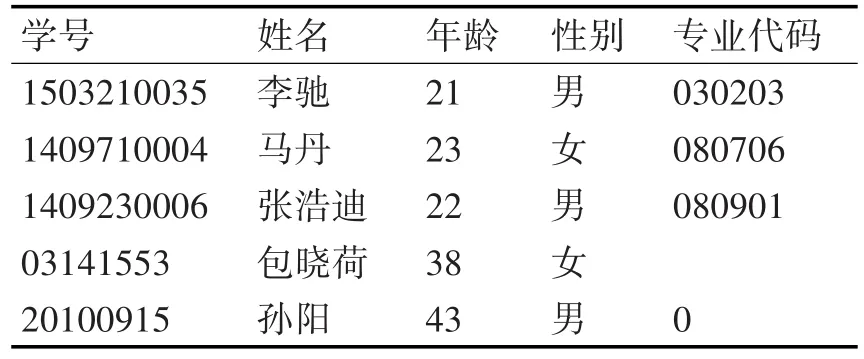
表1 部分师生信息列表
表1为某校部分师生信息的列表。因为数据类型不同,需要将数据统一转换为可计算的数值型数据,如学号、年龄、专业代码是数值型的直接可以参与运算,而姓名、性别字符型的需要转换为数值才可以参与运算。这里均采用Unicode编码将字符转换为10进制的阿拉伯数字。如:姓名字段“李驰”对应10进制Unicode编码为“26446 39536”,性别字段“男”对应10进制Unicode编码为“30007”,之间转换可以通过函数得以实现,表中的空值则默认为0。以表1为例进行属性约简,过程如下:
1)构建决策矩阵。

2)标准化处理后,应用式(6)计算出每个属性值所占比重,可得A对应的矩阵

3)数据集共5条数据,n=5;Inn=1.6094,根据式(7)、(8)计算可得表2结果。
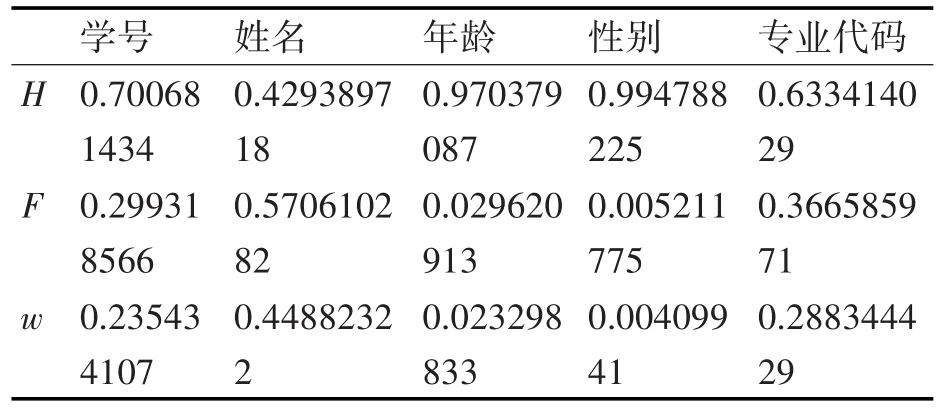
表2 师生信息属性熵值、区分度、权重计算结果
所以,根据表1信息利用熵值法计算得出表2,各属性权重所占比例:学号约占23.5%,姓名约占44.9%,年龄约占2.3%,性别约占0.4%。专业代码约占28.8%,性别权重最小,可以视为非重要属性去除。
如果数据集中存在属性字段较多,可根据实际情况,保证数据检测精度允许范围内人为选择需要保留属性字段个数,实现数据维度的约简,此步骤可以减少后续记录匹配阶段的匹配次数,提高检测效率。
4 相似记录匹配
在初步聚类分组和属性约简后,需要对聚类的小数据集进行相似重复记录的检测。由于数据类型的多样性,可能存在数值型,中英文字符串等。
数值型数据可直接进行计算,如年龄、身高、日期等。将数据集中数据映射到空间中的点,两条记录之间的相似性直接可以用空间距离反映,距离越远说明差异越大。点x,y直接的距离D(x,y)可表示为

对于长度较短的英文或中文,如:姓名,性别,可以数据采用Unicode编码映射成为阿拉伯数字,利用式(9)计算两字符串之间的相似度。
而对于长度较长的字符串,如:地址,采用编辑距离法计算字符串相似度。可以通过直接将字符串中的每个汉字转化为音形码,再将所有音形码合并起来进行计算。字符串s1,s2直接的距离D(s1,s2)可表示为

其中d表示讲字符串s1转换为s2替换、插入、删除字符所需的最少编辑操作次数。
这里采用单个字段逐条匹配。选择权重最大的属性计算该属性下的各个数据值之间的距离,根据字段设置阈值θ判断该字段值的相似性,再按照属性权重大小逐一比较各字段值,直到整条记录所有属性比较完成为止。基于属性权重的相似记录匹配步骤:
Step1:计算出各属性权重并选择最大属性权重的字段;
Step2:计算数据集中该属性下各记录值的相似度,大于该字段阈值则为相似,小于为不相似;
Step3:判断是否比较到最后一个属性,是则判定该条记录为相似记录,算法结束,否则继续执行Step1。

图3 基于属性权重的相似记录匹配流程图
在每个分组的聚类簇中并行化执行该算法,每个小数据集中可判断出相似的记录。该算法需要对每个属性字段设置阈值θ,阈值θ根据经验设定,设置大了,容忍度提高,造成误判;设置小了,造成漏判,所以需要根据实际应用反复尝试,看结果是否到达最优。
5 实验设计
5.1 实验环境
实验采用 Intel i7 2.6 GHz CPU,物理内存8GB,硬盘空间500 GB,操作系统是Windows 7,数据库软件使用MY SQL,程序使用C++语言和Mi⁃crosoft Visual Studio 13.0开发平台。实验数据来源于某校信息中心包括学生基本信息、学生到课数据、校园卡消费数据等,由于数据来源多样,学生日常活动的重复性和历史数据的积累。
5.2 实验设计
为了检验论文中检测算法的有效性,随机提取定量的数据作为实验数据,人工软件结合的方式将相似重复数据量处理成一个准确占比,通过实验结果的对比从三个主要指标查全率、查准率和运行时间进行验证。
从信息中心管理系统中分次随机提取5000,10000,20000,50000,100000,200000条记录的数据量,分别将数据处理成包含包43,89,208,479,789,1980条重复记录的数据集。数据含属性53个,包括学号、姓名、所属院系、学院代码、专业、班级、年级、身份证号、一卡通号、考勤类型、签到时间、综合成绩、电话、家庭住址、宿舍等,表3只列出部分属性字段及数据记录。

表3 在校师生信息列表
从表4中试验结果看出,保留属性权重和占比达80%以上时,查准率和查全率均接近于90%,保留属性权重和占比96.7%时,查准率和查全率都高于98%。经过多次试验表明,保留属性权重和占比达95%以上时,可将误差控制在容忍误差内。

表4 保留属性数量与检测精度对照表
在文献[13]中提出的根据属性权重的分组方法实际也是先对数据进行聚类,在小数据集中检测相似重复记录,为提高检测精度采用了多趟分组查找技术,该方法具有较好的检测结果。因此选择等级分组方法作为本文的对照,为便于处理,等级分组检测法法命名为WGM(Weight Grouping Meth⁃od),本文检测方法命名为 BKCM(Based on K-modes Cluster Method),分别已处理过的数据集完成检测。为了实验具有可比性,两种方法的分组数和聚类个数和阈值都取相同的值,在小数据集检测中都采用多线程并行完成,在BKCM方法中保留属性权重和占比95%的属性以确保检测精度。
5.3 实验结果及分析
表5、表6、图4、图5为两种方法在查准率和查全率的比较,从中可以看出BKCM方法的查准率和查全率都不低于WGM方法,随着数据量的增大两种方法都会略微下降,且BKCM是在设置约简属性的情况下,如果人为设置更低的容忍度,增加保留属性个数,检测精度也会更高。

表5 WGM与BKCM方法查准率比较

表6 WGM与BKCM方法查全率比较

图4 WGM与BKCM方法查准率比较
从表7两种方法的运行时间上可以看出,BKCM在检测同量的数据时完成的时间要小于WGM,在数据量增加时优势也越加明显,原因在于在小数据集检测过程中,BKCM约简了记录属性个数,减少了记录相似匹配次数,缩短了检测时间,对于大量数据处理效果更明显。

图5 WGM与BKCM方法查全率比较

表7 WGM与BKCM方法时间比较
通过多次试验,BKCM方法在检测精度和时间效率上都和理论分析是一致的,总体都优于WGM方法的相似检测方法,尤其是对于数据属性维度非常多的数据,检测效果明显。
6 结语
本文针对相似重复记录检测问题展开了研究分析,采用了多种有效的策略和方法。首先应用K-means聚类方法对于数据进行处理,运用聚类本身特点在簇中查找相似记录更为有效。其次,为提高检测效率再依据属相权重对属性进行约简,并在检测过程中采用多线程并行处理。实验表明,该方法能有效地检测相似重复记录,对提高数据质量有着显著效果,同时也对上层数据应用分析阶段提供了可靠的数据信息。但在实际使用中发现该方法仍有一些问题需要解决,如:聚类簇个数以及字段阈值设定的问题,都需要人为干预进行,由于这两个指标设定对记录检测的精度有一定影响,所以针对这些不足后续工作还需要进一步研究。
