一种改进的ID3决策算法及其应用∗
2019-12-27圣文顺孙艳文
圣文顺 孙艳文
(南京工业大学浦江学院 南京 211222)
1 引言
决策树分类方法是一种有效的实例学习[1]和数据挖掘[2]方法,当前最有效的决策树分类算法是Quinlan在1986年提出的ID3算法,其中决策树以自顶向下递归的分治方式构造[3]。ID3算法的思想是将所有实例(或者数据库中的数据)作为决策树的根节点,按照信息论方法中熵[4]的概念来度量各项属性的信息度,以此作为选择属性的依据,根据属性值对树根进行分裂,建立分支节点;然后将每个分支节点分别作为根节点,重复进行“选择属性——分裂树”的操作,直到最后的分支节点仅包含正例或者反例,构建成一棵完整的决策树[5]。
2 ID3算法理论
对于有大量实例数据的归纳学习,常采用ID3算法。实例数据[6]一般都是混乱无序的,归纳学习[7]的目的就是从无序的数据中找出内在蕴涵的规律。实例数据一般都基于属性理论,这样就允许使用信息论方法来测试特定属性值从而进行分类。ID3算法的核心思想是将Shannon的信息论方法[8]引入到属性选择中。ID3算法通过把每个属性当作当前子树的根节点来度量信息增益[9]。
Shannon的信息论方法提供了度量一条信息的信息量的数学基础。将一条信息看成是可能信息空间的一个实例;传播信息的动作就相当于从可能的信息中挑选出一个。从这个观点来看,定义一条信息的信息含量依赖于这个空间的大小、每个可能的信息的出现频率。对于实例学习,可将每一实例的属性看作一条信息,属性的选择即可从属性的信息量出发,优先选择信息量高的属性生成决策树。
ID3算法中信息论方法形式化如下:设作为训练集的实例数据集合为X,ID3学习的过程是将该实例数据集合根据某一属性A的属性值分为n类,记为{c1,c2,…,cn},第i类的实例数据的个数计为|Xi|,—个实例数据属于第i类的概率为p(Xi|A=ai),则有:

概率p(Xi|A=ai)即为属性A的属性值等于ai的概率。给定属性取值空间和每一属性值出现的概率,那么可定义该属性值的信息含量数学期望值:
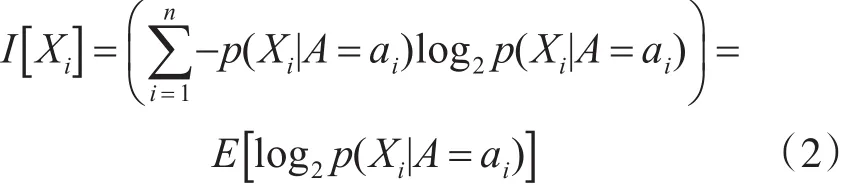
对于实例集X,最终会将其分为n类,设为{c1,c2,…,cn} ,则有决策树划分X的信息量为

选择属性A后,对划分出的每个子集,可得:

根据信息论方法,在当前树的根节点做测试所提供的信息增益与树的总的信息量减去测试完成后完成分类索溪的信息量相等,则有:

式(5)即为属性A的信息增益,信息增益越大,说明选择该属性进行决策树的划分带来的不确定性越小,越能快速的构建好决策树。ID3算法基采用Gain(A)[10]作为选择测试属性的依据生成决策树。
3 ID3算法改进
由ID3算法可知,信息增益最大要求I[X]值尽量大。研究表明,采用加权和计算[11]的选择方式往往倾向于选择取值较多的属性,而抛弃取值少的属性。然而在实际中,取值多的属性并不一定是主要属性,取值少的属性不一定是非主要属性,这种属性称为噪声[12]。现提出对ID3算法进行改进——对每项属性的权重加以修正,在选择测试属性时,不再以属性的取值多少作为主要依据。
设修正权值[13]为a,取值区间为[0,1],该权值由用户根据先验知识确定。先验知识[14]是指先于经验的知识,具体包括领域知识和专家建议。先验知识调节其对分类的信息量,提高分类的准确性,应用到决策树学习中,除了用于生成和修改决策树的实例集之外,还包括所有影响决策树规则生成和选择的因素。先验知识是一个模糊概念,可使用模糊集概念[15]来辅助确定。
改进的ID3算法主要步骤如下:在式(4)中加入α,可得:

相应的增益为

改进的算法使用式(6)和式(7)来代替原式生成决策树。
4 算法验证
本文通过分析HR选择就职人员的记录,应用改进后的ID3算法生成符合就职的决策规则。示例样本数据见表1。

表1 样本数据
对于覆盖所有历史样本数据的树的信息含量为
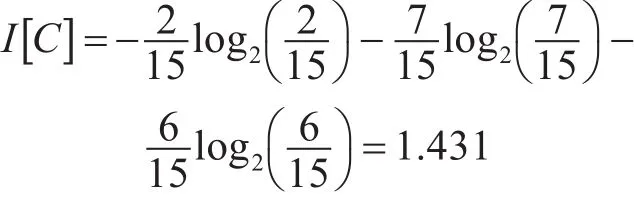
假设选择历史样本数据的属性“专业”作为决策树的根节点,可将历史样本数据分为C1={1,14}、C2={2,4,5,8,10,11,13,15}和 C3={3,6,7,9,12},分别对应“专业”属性取值为“国际贸易”、“通信与信息系统”和“计算机科学与技术”的取值分类。根据先验知识,对性别、年龄、学历、专业分别设修正权值为0.3、0.2、0.1、0。完成树所需的信息量数学期望为

即选择专业属性测试的信息增益为0.304。
类似可得:
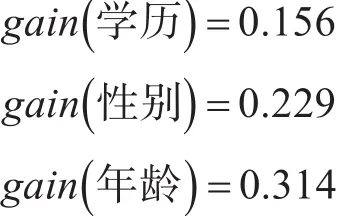
对应所得的决策树为

图1 决策树
5 结语
上述算法示例表明,在原有ID3算法中加入属性修正权值,同样能够生成决策树,且具有可行性。加入修正权之后,ID3决策树的生成不再仅仅依赖于属性的信息量,先验知识也能够对决策树的生成起到影响,可以对算法中噪声的产生起到抑制作用。
先验知识的获得和表示是该改进算法的重要部分,如何确定属性修订权值直接影响了改进算法的效果。先验知识的处理属于模糊集合问题,可用粗糙集概念[16]对其进行形式化描述,已有不少学者在这方面进行深入研究,这也是下一步研究工作的重点。
