基于灰色马尔科夫链模型的CT球管故障间隔期预测

邱春冬 杨玉志 王春云

南京大学医学院附属鼓楼医院 临床医学工程处，江苏南京 210008

在实际维修工作中，CT球管出现的故障次数较少，是典型的小子样和贫信息系统，因此考虑选用灰色模型来对CT球管的故障间隔期进行预测。灰色GM(1,1)模型的预测数据比较平滑，在对服从指数分布的序列进行预测方面具有一定的优势，但是如果序列数据随机波动比较大，那么用灰色GM(1,1)模型预测就不能保证预测的可信度[1-3]。因此，本文在灰色GM(1,1)模型的基础上建立灰色马尔科夫链模型来对CT球管的故障间隔期进行预测，灰色马尔科夫链模型对兼具趋势性和波动性的非平稳随机序列具有很好的拟合效果，能更好的表达数据的变化规律[4-6]。

1 灰色GM(1,1)模型

灰色GM(1,1)模型是灰色预测理论体系中使用最广泛的灰色预测模型，它是关于数据序列预测的一个变量的一阶微分灰模型[7-9]。根据现有的原始数据序列，通过时序累加生成新的数据序列，新的序列呈现的规律可以用一阶线性微分方程进行拟合，拟合后的数据序列可以揭示原始数据序列的变化规律。数字化放射设备的故障率数据，多数属于序列短、信息量少、规律性不强的数据，符合贫信息系统特征，因此可以用灰色GM(1,1)模型对其故障率进行预测[10-13]。

灰色GM(1,1)模型预测值函数：

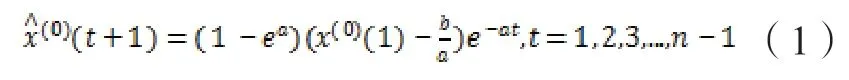
2 灰色马尔科夫链模型

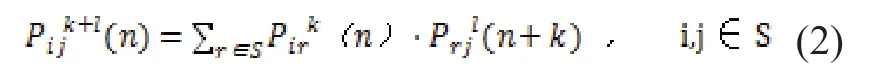
公式(2)称为Chapman-Kolmogorov方程，简称C-K方程。C-K方程说明对于步数较高的转移概率矩阵可以用步数较低的转移概率矩阵来表示。即可以用k步转移概率矩阵P(k)表示：Pk+l=Pk·Pl。令k=l=1，有Pk+l=P1·P1'=P2，利用数学归纳法逐渐递推可得P(k)=Pk，即k步转移概率矩阵P(k)可以用一步转移概率矩阵P来表示。

2.1 灰色马尔科夫链模型构建过程

2.1.1 状态划分 按照灰色GM(1,1)模型的预测原理，对已知的原始数据序列x(0)求出其预测值，由此可得残差序列[14]：

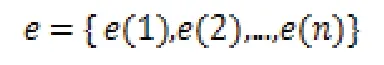
其中：

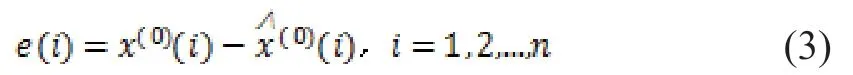
误差：

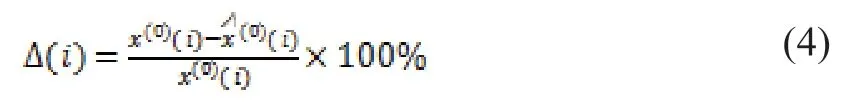
根据误差大小进行状态划分，共划分r个状态，每个状态间隔相等，记为Eij=[Lij,Uij]，j=1,2,…,r，此处Lij，Uij分别为残差序列的第i步的第j个上下边界：

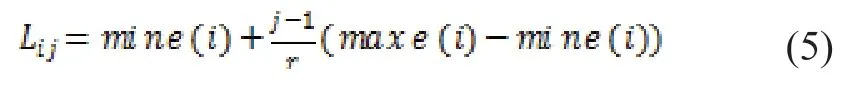
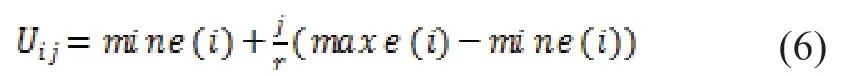
2.1.2 计算状态转移概率矩阵 状态转移概率为：

式中：Mij为状态Ei经m步转移到状态Ej的原始数据样本数。根据误差大小将残差序列e划分为r个状态，构成r*r阶的一步转移概率矩阵，它反映了原始数据序列状态转移规律[15]。

2.1.3 获取预测值 确定系统的一步状态转移概率矩阵后，对矩阵的行向量进行分析，可以得到预测数据序列从当前状态转移到下一状态的概率，记为：Ei(t)，i=1,2,…,r，t为转移时间。区间的中点被视为每个区间可能的预测值[16]，则将来状态的预测值按下式计算：

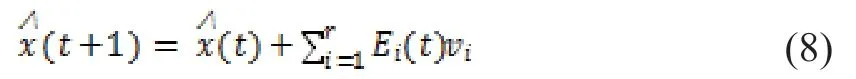
这里：

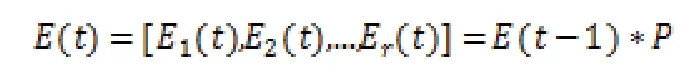
这样就计算出下一个预测数据处于何种状态，从而可以计算出预测值为

3 实例分析

x线球管存在其特有的生命周期，以球管的总扫描时间来衡量，一旦达到其设计寿命上限，球管发生灯丝断裂或旋转阳极损坏的概率将大大增加。以某型号CT球管总使用时间为例。对实际工作中收集的数据进行整合分析，得到某型号CT每一个球管的发生故障时已扫描的时间，见表1。

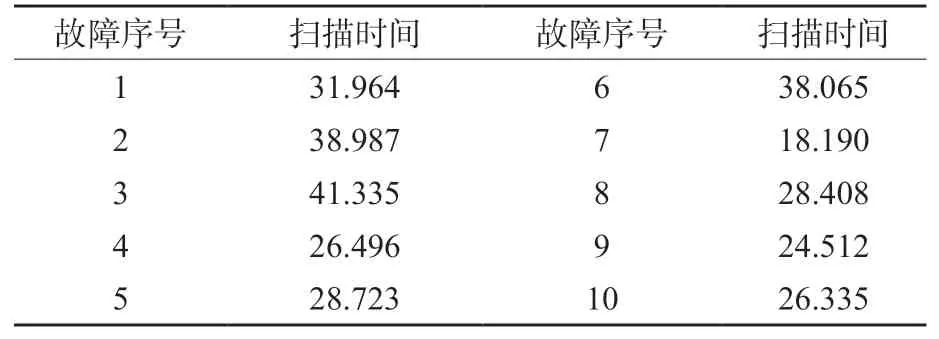
表1 某CT球管故障时扫描时间（单位：万秒）

3.1 灰色GM(1,1)预测故障间隔期

利用表1中前9次数据为原始数据序列，对第10次数据做预测，得到球管故障间隔期原始序列为：

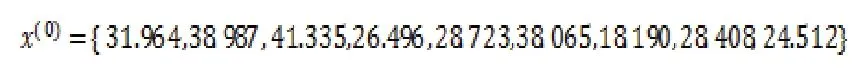
代入公式，利用Matlab软件，计算B和Y的值，并代入公式计算得到发展系数a和灰作用量b的值为：a=0.0729，b=585.7142。灰色GM(1,1)模型的预测值函数为：

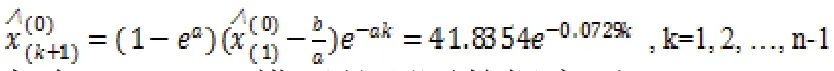
灰色GM(1,1)模型的预测数据序列：

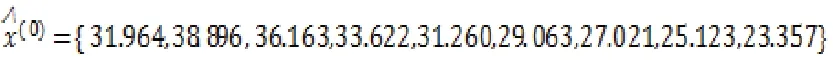
将预测值和实际值进行拟合，如图1所示。从图中可以看出CT球管的故障间隔期总体呈下降趋势，说明随着CT使用年限的增加，电子部件的老化以及其他因素的影响，球管发生故障的间隔期越来越小，比较符合CT设备运行的一般规律。

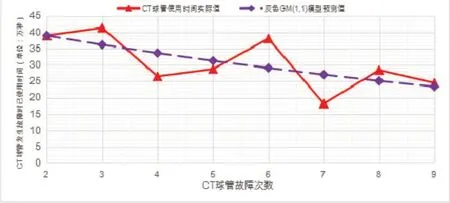
图1 某 CT球管使用时间实际值与灰色GM(1,1)模型预测值比较

3.2 灰色马尔科夫链模型预测故障间隔期

3.2.1 状态划分 表2为球管扫描时间实际值和灰色GM（1,1）模型预测值的比较，分析相对误差状态，可划分为四个状态区间，状态1：E1=(-49，-30]；状态2：E2=(-30，-12]；状态3：E3=(-12,7]；状态4：E4=(7,24]。

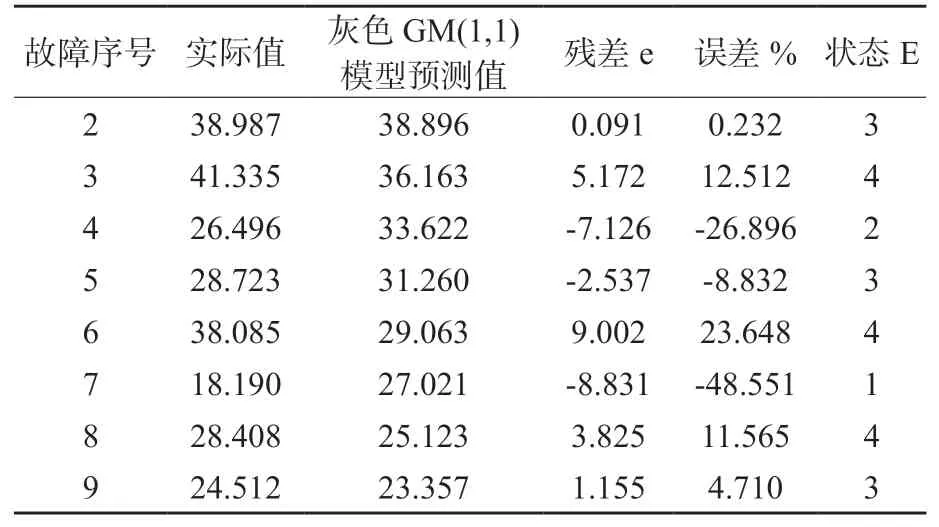
表2 某CT球管扫描时间实际值和灰色GM（1,1）模型预测值比较

由此可计算每个状态的中间值为M1=-39.5%，M2=-21%，M3=-2.5%，M4=15.5%。

3.2.2 故障间隔期的预测 由表2可以得到每次故障所在的状态区间，利用残差相对值公式，可得到预测值为：

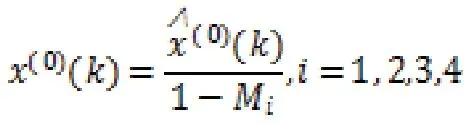
得到灰色马尔科夫链模型的预测数据序列为：

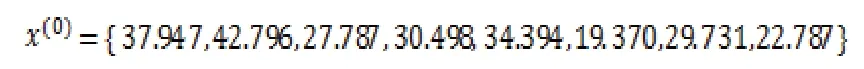
3.2.3 误差分析 一个模型能否用于预测，预测的效果好坏，需要用模型评定指标来进行衡量。在统计学预测方法中，平均绝对百分误差（MAPE）是最常用误差标准之一，可作为预测模型的评价指标：

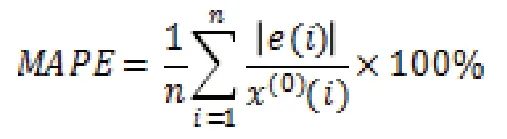
其值越小越好，它反映了原始数据序列和预测数据序列的差异程度，可以为预测结果的可靠性提供客观的依据。

灰色GM(1,1)模型与灰色马尔科夫链模型的实际值与预测值的误差见表3。

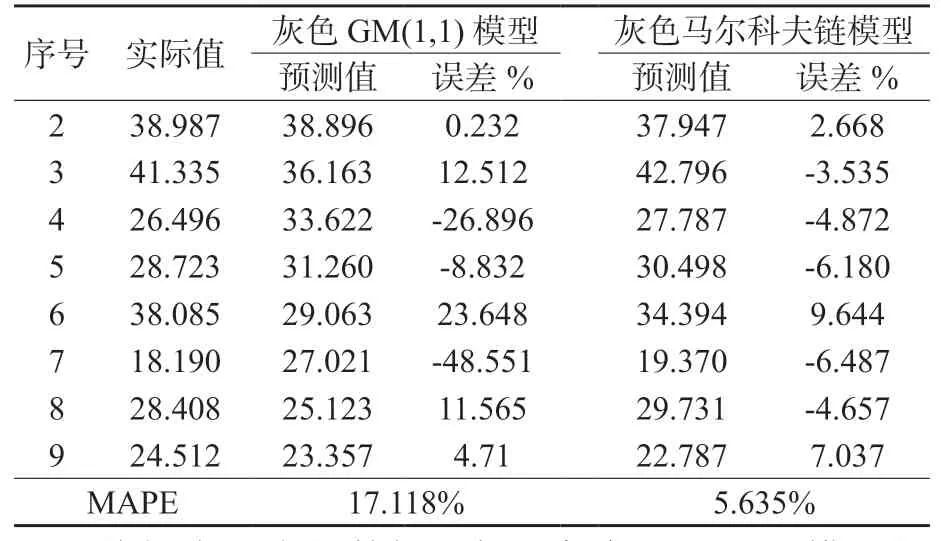
表3 两种模型预测误差分析

分析表3中的数据可知，灰色GM(1,1)模型的MAPE为17.118%，灰色马尔科夫链模型的MAPE为5.635%，说明灰色马尔科夫链模型的预测数据更加契合原始数据序列，也表明将灰色GM(1,1)模型与马尔科夫链理论相结合可以有效地预测CT球管的故障间隔期。如图2为两种预测模型的预测结果与实际值的比较图。

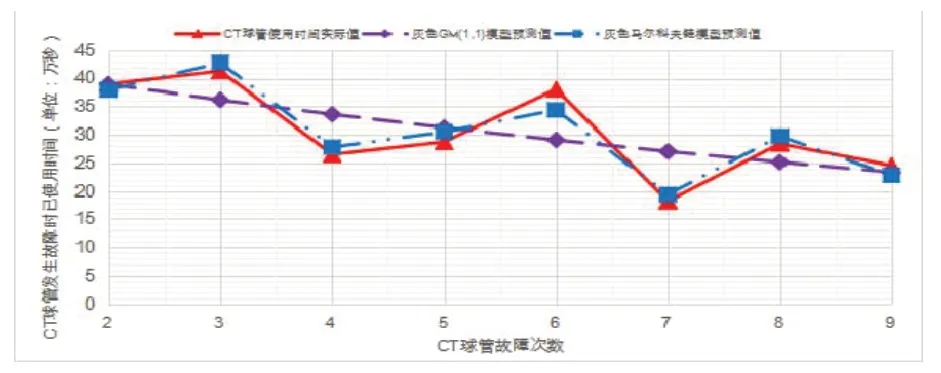
图2 某CT球管故障间隔期原始值与两种模型预测结果比较图

3.3 灰色马尔科夫链模型对下次故障间隔期进行预测

3.3.1 确定转移概率矩阵 由表3所知，共有CT球管故障间隔期原始数据序列具有8个数据点，由于最后一个点的转移方向不明，因此只考虑前7个点，根据实际数据的情况和状态划分情况，共有3个点处于第一状态，其中有2个点处于第二状态，有2个点处于第三状态，故可以确定一步转移概率矩阵P1为：

3.3.2 预测下次故障间隔期 由预测数据的状态划分结果可知，CT球管第9次发生故障时，它所处的状态为状态3，那么CT球管下一次发生故障时，它所处的状态可以由一步转移概率矩阵P1确定。因此，可知经一步转移后，CT球管第10次发生故障时它处于状态4的位置。利用公式得到灰色GM(1,1)模型预测CT球管第10次发生故障时，球管已使用的时间为：

根据灰色马尔科夫链模型的预测公式，可以计算得到CT球管第10次发生故障时，球管的使用时间所处的区间为（23.341,28.562），最终获得灰色马尔科夫链模型的预测值为：

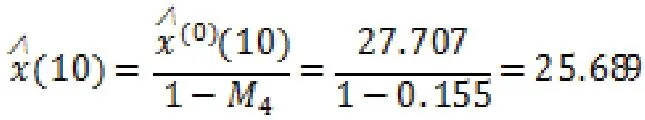
实际上，第十次更换球管时，球管的使用时间为26.335万秒，在此区间内，与预测值的误差为2.453%。

4 小结

通过CT球管故障间隔期预测的实例分析，表明在少数据，贫信息，不确定的情况下利用该灰色马尔可夫链模型预测CT球管故障间隔期的有效性，可综合体现灰色预测和马尔科夫链预测的优点，它可以有效降低预测误差，提高预测精度。用灰色马尔可夫链模型预测CT球管故障间隔期还只是初步探索，期望为设备管理部门制定预防性维修间隔期提供依据，能够指导设备使用科室和管理部门做出良好的设备管理决策，但是由于CT设备运行时随机性和波动性很大，该方法还需进一步深入研究。