基于格的两方口令认证密钥交换协议

赵宗渠，黄鹂娟，叶 青，范 涛

(河南理工大学 计算机科学与技术学院，河南 焦作 454000)

0 引 言

由于现代网络广泛采用客户-服务器的结构，客户远程登录服务器的安全性以及数据传输的机密性已被学术界视为重点问题研究，而适用于客户-服务器认证框架的基于格的两方口令认证密钥交换(password-based authenticated key exchange，2PAKE)协议已经成为应用最为广泛的一种。口令的好处在于简单易记 ，在2PAKE协议中，客户仅凭口令就可以实现安全地登录服务器，并为后续交互生成高熵的会话密钥，而不用担心攻击者通过控制通信信道截获其口令。即通过密码学技术在开放的易受攻击的网络中建立一个安全的通信信道，实现安全的通信。

早期的2PAKE在1992年由Bellovin和Merritt[1]提出，在Diffie—Hellman密钥交换协议的理论基础上，该协议实现了两方相互认证并建立安全的会话密钥，可抵抗在线口令字典攻击。之后，两方的认证密钥交换协议被大量提出[2-5]。2001年Katz，Ostrovsky和Yung[6]在标准模型下构造出高效的PAKE协议，该协议利用CCA2安全的加密体制及相应的平滑投射哈希函数实现密钥交换，简称KOY协议。这些协议需要一个通用的参考字符串(common reference string, CRS)。而舒剑等[7]引入伪随机函数，提出了只需一个生成元，且在同类型的协议中计算开销度最低的协议，协议执行整个过程中，响应方不需要知道私钥，同时实现了双向认证。

传统PAKE协议的安全性绝大多数都是依赖于大整数分解和离散对数问题的困难性，这类数论类型的数学问题在量子算法中被证明不再困难，协议在安全性上也不能得到保障。格上的数学难题目前被认为能够抵抗量子算法攻击，并且具有并行计算、效率高的特点，格困难问题上最著名的算法最短向量问题(shortest vector problem，SVP)需要指数时间和指数空间，早期的PAKE结构也不能用基于格的假设来实例化，为使PAKE能抗量子攻击且更具有实际应用可行性，基于格困难问题的密钥交换协议的研究和设计迫在眉睫。近年来，基于口令的高效认证密钥交换协议被大量提出。

2008年，Peikert和Waters[8]使用有损陷门生成算法和完全基于最坏情况的格假设，构造出第一个基于格的CCA-secure的加密结构，方法更有效，技术更简单，这方案并不适应平滑投射哈希函数的性质，后续的结构[9-12]也不能立即支持平滑投射哈希函数。直到2009年Katz和Vaikuntanathan[13]突破了用KOY[6]和GL[14]方法构建基于格的PAKE协议的障碍，以基于误差学习(learning with errors，LWE)问题的困难性问题为基础，首次提出基于格的CCA安全的加密体制及其相应的近似平滑投射系统，构建了基于格的首个2PAKE协议。

2014年，Peiker[15]提出一种基于环上带误差学习(ring learning with errors, RLWE)的简单低带宽调和函数，构造其密钥封装机制，实现了密钥交换。2016年，利用格困难问题，赵秀凤等[16]提出一种密钥交换协议，因该协议需要密钥生成中心生成长期私钥和临时私钥，成本花销大。为解决两方协议不适应大规模通信的问题，利用DH思想，Xu等[17]基于RLWE问题提出了可证明安全的PAKE协议，客户和服务器之间进行6轮通信，传输的消息量较多，需计算多项式环和多个哈希函数的值，使得通信开销度增加，协议效率降低。

2011年，Ding等[18]把Katz和Vaikuntanathan提出的近似平滑投射系统，应用于Groce-Katz框架[19]中，该框架仅需构建一个具有标签的选择密文攻击(chosen ciphertext attack, CCA)安全的加密体制和一个带有相关近似平滑投射哈希函数的选择明文攻击(chosen plaintext attack, CPA)安全的和带有标签的安全加密体制，与伪随机函数簇相结合，提出了一种高效的基于格困难问题的协议，在标准模型下证明是安全的同时具有双向认证的能力。该协议在一次会话密钥的生成过程中，需要重复利用CCA安全的加密算法来实现客户对服务器的显式认证，增加了计算的复杂度。

2017年Zhang等[20]在Katz的基础上弱化近似平滑投射函数的概念，提出一种投射密钥仅取决于哈希密钥的非自适应平滑投射哈希函数，基于LWE困难问题构造出格上可拆分的公钥加密体制，即加密密文由相互独立的2部分计算组成，并将其应用于Katz等[6]的3次通信框架中，提出一个带有标签的仅需2轮通信的PAKE协议，提高了通信效率，但可分离的公钥加密体系和非交互式零知识证明的复杂代数关系，使得该方案的密钥尺寸和计算开销度都有所增加。

综上所述，为使PAKE更具有实际应用可行性，需要构造更简单、更安全、更高效的PAKE协议，总结和学习前人的思想和方法，本文构造了一种新的格上基于口令的认证密钥交换协议。主要贡献为将格上具有近似平滑投射哈希性质的CPA安全的加密体制和伪随机函数簇相结合，提出格上基于LWE困难性问题的高效2PAKE协议。与同类方案相比，分析表明本文协议减少哈希密钥的生成次数，降低了计算投射密钥的计算开销度，利用伪随机函数计算认证值获得双向认证，避免重复加密口令得到密文的值进行认证服务器带来的计算开销，在服务器和客户的协商下利用随机函数和平滑投射的正确性计算出会话密钥，并证明其安全性。

1 相关知识

1.1 格相关知识

定义1设n维空间上m个线性无关的向量B=(b1,b2,…,bm)，所有这些向量的整系数线性组合定义为格Λ⊂Rm，即为

(1)

(1)式中，向量组b1,b2,…,bn构成格的一组格基。

定义2离散高斯分布。对于任意s>0，以向量c∈Rm为中心、s为参数的格Λ上的离散高斯分布函数定义为

(2)

(2)式中，x∈Λ，ρs,c(x)=exp(-π‖x-c‖2/s2)。

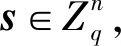
(3)

(3)式中，对于取自As,α的任意m个采样(a1,b1),…,(am,bm)，其矩阵形式表示为

(4)

(4)式中，A=(a1,…,am)，b=(b1,…,bm)t。

1.2 近似平滑投射哈希函数

Cramer和Shoup首次提出了平滑投射哈希函数，文献[13]将其应用于基于格的PAKE协议，构造了格上的近似平滑投射哈希函数，本文就采用此平滑投射哈稀函数。

2)平滑性。对任意的x=(c,pw)∈XL，Hk(x)统计上接近均匀分布x和α(k,label,c)。

1.3 公钥加密体制

一个带标签的基于格困难问题LWE假设的CPA安全的公钥密码体制PKE′=(KeyGen′,Enc′,Dec′)，它的明文空间为P。

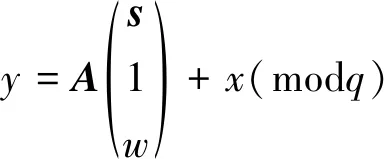
(5)

4)解密算法。对于正整数a=1到q计算得

(6)

(6)式中，如果a′=a输出w/a停止，否则尝试计算下一个有效的a,如果所有的都失败输出。

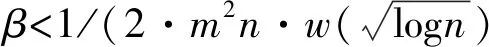
1.4 安全模型

在Bellare等[21]提出的BPR模型基础上给出了本协议的安全性分析模型。在协议执行之前，可信第3方制定公共参考串(common reference string, CRS)和其他公共参数。

协议参与方：在两方协议中，所有参与方由客户u∈U和诚实可信服务器S∈s组成，其中，U表示协议用户的集合。

长期密钥：在基于口令的协议中长期密钥就是口令，用户u∈U具有口令pwU，诚实服务器和客户共享口令pws=(pwU)u∈U，从字典集合D中独立均匀地选择口令。

攻击者A拥有控制所有信道的时间概率多项式算法的权利；可截获所有明文信息，读取它们并修改成自己意定的信息；A可以获取实例的会话密钥，模仿会话密钥可能泄露的信息。

定义4(安全性)设口令字典空间为Dn，Q(k)表示主动攻击的会话次数，其中k是与安全参数无关的常量。若对任意概率多项式时间的攻击者A至多可进行Q(k)次在线攻击，且满足Adv∏A(k)≤Q(k)/Dn+negl(k)，则称PAKE协议Π是安全的。

2 基于格的两方PAKE协议

2.1 协议描述

本节在Groce-Katz框架下，应用具有近似平滑投射哈希函数的CPA安全的公钥密码体制PKE′=(Gen′,Enc′,Dec′)和具有标签的CCA安全的加密体制PKE=(Gen,Enc,Dec))设计了一种改进的2PAKE协议。

设n为安全参数，ε∈(0,1)是一个极其微小的实数；客户和服务器共享其口令为pw，pk′和pk分别是CPA和CCA安全的公钥密码体制的公钥，并且作为公共参考串，在协议执行前由可信第三方用公钥生成算法KeyGen(1k)生成，系统中没有用户知道与之对应的私钥；CPA安全的密码体制PKE′的Hash函数簇是H={Hk}k∈K，定义域为X，值域为{0,1}n，Hash函数的密钥空间是K；伪随机函数簇F={Fδ:δ∈(0,1)l}l∈N，协议描述如图1。

客户与服务器执行过程如下。

1)客户Client选择随机值rc∈(0,1)，用PKE′对口令pw加密得到密文Cc，从哈希密钥空间K中随机选择密钥kc，通过投射函数α(kc,Cc)计算投射密钥sc。最后向服务器Server发送消息〈Client|Cc|sc〉。

2)服务器Server收到来自客户Client的消息〈Client|Cc|sc〉后，先选择随机数rs←{0,1}，让CCA安全的公钥加密体制的标签为label=〈Client|Server|Cc|sc〉，用PKE对口令pw加密得到密文Cs，从哈希密钥空间K中随机选择哈希密钥ks，用投射函数α(ks,Cs)计算投射密钥ss。通过近似平滑投射函数计算哈希值tk，令随机数δ=tk，计算ms=Fδ(1)。然后向客户Client发送响应消息〈Server|Cs|ss|ms〉。

3)客户Client收到来自服务器Server的消息〈Server|Cs|ss|ms〉后，同理可得哈希值tk′，然后计算认证信息ms=Ftk′(1)对服务器进行认证，若认证不通过则终止协议，否则计算mc=Ftk(3)，会话密钥SK=Ftk′(2)。然后向服务器Server发送〈mc〉。

4)服务器Server收到客户Client的消息〈mc〉，计算mc=Ftk(3)进行验证，若不相等则终止协议，否则计算相应的会话密钥SK=Fδ(2)。

Common reference string: pk’,pkClient(pw) Server(pw)rc∈(0,1)∗Cc=Encpk′(pw,rc)kc←K; Client|Cc|ss →rs∈(0,1)∗ ks←K;ss←α(ks,Cs)lable=Client|server|Cs|scCs=Encpk(label,pw,rs)tk=Hks(Cc,pw) Hash(sc,Cs,pw,rs)tk′=Hkc(Cs,pw)Server|Cs|Ss|ms←δ=tk;ms=Fδ(1)Hash(ss,Cc,pw,rc)验证: ms=Ftk′(1)mc=Fδ(3)SK=Fδ(2) mc →验证:mc=Fδ(3)SK=Fδ(2)

图1格上的两方PAKE协议

Fig.1Two-partyPAKEprotocolbasedonlattice

协议第2轮客户收到服务器发送的密文Cs、投射密钥Ss和验证值ms，通过平滑投射函数的性质计算tk′，验证ms的正确性实现客户对服务器的显式认证。协议的最后客户向服务器发送通过哈希值tk′计算的认证码mc，服务器计算并验证mc的正确性，实现对客户的显式认证，因而该协议获得了客户和服务器之间的双向认证。

正确性：对于所有诚实的参与方，在协议执行后，获取不相同的会话密钥的概率是可忽略的。由ASPH的近似正确性可知Hash(s,c,pw,r)和Hk(c,pw)的汉明距离大于ε的概率是微乎其微的，则tk和tk′的汉明距离至多为2ε是可忽略的，客户和服务器会得到相同的δ，以及伪随机函数簇的正确性，所以客户和服务器能获得相同的会话密钥。

前向安全性：假设攻击者获得了用户的口令pw，同时截获了其发给服务器的密文和投射秘钥，想要计算出前一次的会话秘钥SK=Fδ(2)，就得知δ=tk′=Hkc(Cs,pw)⊕Hash(ss,Cc,pw,rc)，由于用户选择任意的随机值rc∈(0,1)加密密文，而攻击者不能从以上信息中恢复出随机值rc∈(0,1)和哈希秘钥kc，即无法计算出tk′，所以不能获得以前的会话秘钥。

2.2 安全性证明

本节在1.4节所述的安全模型下证明其安全性。

定理2假设n是安全参数，Dn是口令空间，基于格的具有近似平滑投射哈希函数的CPA安全的公钥密码体制为PKE′，和格上带有标签的CCA安全的公钥加密体制PKE，F=F{Fδ}是伪随机函数簇，则本文所提出的是具有明确身份认证的安全协议。对于攻击者A存在可忽略函数negl(k)、计算时间最多为t、询问次数至多为Q(k)次的敌手A，有Adv∏A(k)≤Q(k)/Dn+negl(k)成立。

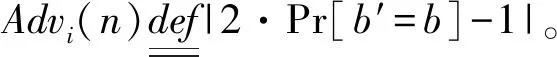
试验Γ0这个试验相应于安全模型中对实际协议的真实攻击。在连续的实验中，比较相邻试验的优势差，最后分析攻击者在试验Γ0中的优势。

试验Γ1我们修改Execute询问的模拟方式。模拟者选择任意的口令pw0，计算Cc=Encpk′(pw0)作为对攻击者发出询问的响应。使客户计算的tk′设置为与服务器的tk值一致，其他计算与真实协议一样。

引理1|Adv1(n)-Adv0(n)|≤negl(n)。

证明这是PKE′的直接描述方式，假定一个多项式时间的敌手M攻击密码体制PKE′：已知公钥pk，敌手M模拟整个实验，包括选取任意口令。将(PW,PW0)作为M的挑战明文对响应Execute询问，将Execute询问中的Cc用挑战密文c代替。因M可以完全模拟真实的协议，即可以计算正确的tk，最后对Test询问中的随机比特做猜测，若A攻击成功则M输出1；否则M输出0。可知M成功的概率为|Adv1(n)-Adv0(n)|，所以由PKE′的安全性可知引理结论成立。

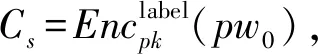
引理2|Adv2(n)-Adv1(n)|≤negl(n)。

证明这个引理是基于PKE的,事实上我们依靠CCA的安全性构造一个多项式时间的敌手M攻击协议，给出公钥pk，敌手模拟整个实验为攻击者A。在回答Execute询问时，M将挑战明文对(PW,PW0)生成的密文C代替Execute询问中的ms。注意M可以完全模拟真实的协议，即可以计算正确的SK，最后对Test询问中的随机比特做猜测，若A成功则M输出1；否则M输出0。可知M的区分优势为|Adv2(n)-Adv1(n)|，由PKE的安全性可知引理结论成立。

试验Γ3在试验Γ2的基础上修改Execute询问中的计算，用直接选取的随机数代替tk的值，而不是利用近似平滑投射函数的正确性计算。

引理3|Adv3(n)-Adv2(n)|≤negl(n)。

证明从近似平滑投射函数的性质得出，因Cc和Cs被替换为虚拟口令的密文，对于近似平滑投射函数(Cc,pw0)和(Cs,pw0)是一个非法输入，输出被视为均匀分布，统计距离最多是可忽略的。攻击者可以进行Q(x)次询问，故最终引起的概率差是可以忽略的。

试验Γ4修改Execute询问中的伪随机函数，假设Fδ(i),i=1,2,3是独立均匀选择的随机数。

引理4|Adv4(n)-Adv3(n)|≤negl(n)。

证明从试验Γ3可知，客户与服务器已经拥有了相同的tk，因此将获得相同的δ。我们假定敌手M攻击伪随机函数簇Fδ，且拥有无限大的能力。在响应Execute询问时，M对其输入进行询问，用其回答替换Fδ(i),i=1,2,3。若A成功,则M输出1；否则M输出0。可知M的概率差为|Adv4(n)-Adv3(n)|，所以由伪随机函数簇可知引理结论成立。

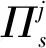
引理5|Adv5(n)≤Adv4(n)|。

试验Γ6对协议模拟作技术上的处理。若客户C收到Send(C,i,Server|Cs|ss|ms)询问，且判断〈Server|Cs|ss|ms〉是匹配生成的，强制令客户与服务器实例获取相同的tk。由于tk对攻击者是隐蔽的，故此修改不影响攻击者的成功概率。

引理6|Adv6(n)≤Adv5(n)|。

试验Γ7我们修改Send0询问。如果客户被Send0=(C,i,S,j)激活，则利用虚拟口令pw0计算密文Cc=Encpk′(pw0,rc)。

引理7|Adv7(n)-Adv6(n)|≤negl(n)。

证明模拟者需记录与pk′相应的私钥sk′之外，该证明和引理1的证明相似。从试验Γ5起，我们进行被动攻击测试，利用具有的解密能力来响应形如Send(C,i,Server|Cs|ss|ms)的询问。

实验Γ8模拟者拥有与公钥pk对应的私钥sk。对Send(S,j,Client|Cs|ss)询问，如果〈Client|Cs|sc〉不是由C的实例生成的，则利用私钥进行解密pw0′=Decsk(Cc)，若pw=pw0′，则攻击者成功并停止模拟，然而这并不减少攻击者成功的概率。

引理8|Adv7(n)≤Adv8(n)|。

实验Γ9修改Send(S,j,Client|Cc|ss)询问。〈Client|Cc|sc〉可能是客户实例生成的，也可能不是，但是解密得到的pw和pw0不相等，假设服务器端的tk值为随机值。

引理9|Adv9(n)-Adv8(n)|≤negl(n)。

证明实验Γ7中用虚拟口令pw0的密文替换Cc，对于ASPH函数(Cc,pw0)是一个非法输入，其输出被视为均匀分布，故最终引起的概率差是可以忽略的。

实验Γ10Send询问中让独立均匀选取的随机数作为Fδ(i),i=1,2,3的值。由伪随机函数簇的性质可知，攻击者不能区分Γ9 和Γ10 的优势。

引理10|Adv10(n)-Adv9(n)|≤negl(n)。

实验Γ11在这个实验中我们修改Send(S,j,Client|Cc|sc)，用虚拟口令pw0所对应的密文将服务器端的密文Cs替换。

引理11|Adv11(n)-Adv10(n)|≤negl(n)。

证明此引理和引理1的证明类似，不同在于此处利用PKE，从实验Γ5起，我们需要事先获取私钥sk，解密密文来回答针对客户的Send(C,i,Server|Cs|ss|ms)的询问。至此与客户C相关的所有Send询问的修改试验都已完成，对实验Γ11中攻击者成功的概率进行分析。假设攻击者猜错口令，则攻击成功只能猜对随机比特b，因用随机值替换会话密钥，故攻击者猜对b的概率是1/2；同时如实验Γ5，Γ8所述，攻击者每次能通过猜测口令成功的概率至多为1/Dn，在Q(k)次试验后攻击者最终的概率为Q(k)/Dn。综上试验Γ1—Γ11所述，可知AdvΠA(k)≤Q(k)/Dn+negl(k)正确，即定理2结论成立，定理证毕。

3 协议性能分析

本节在安全性和效率上，与KATZ等[13]提出具有近似平滑性的PAKE协议，Ding等[18]提出高效的PAKE协议， Zhang等[20]提出格上可分离公钥加密体制的PAKE协议，Zhou等[22]提出基于LWE的强安全AKE协议相比较。在安全性方面，新的协议是基于格的抗量子攻击的，可双向认证，具有可抵抗不可检测在线字典攻击的能力；在效率方面，本文协议客户端使用CPA安全的公钥加密体制加密口令，减少加密参数，降低计算复杂度。与文献[18]相比，用伪随机函数计算认证值，避免重复加密密文来认证服务器，使本协议的效率提高。尽管本协议与文献[18，20]所用哈希函数个数相同，但是本文哈希函数是基于CPA的参数计算相比之下更简单。分析如表1。

表1 协议性能分析

文献[13]是格上具有近似平滑性且需3轮通信的2PAKE协议，通信代价主要取决于密文、投射密钥和一次性验证签名，与本方案相比，公钥尺寸大，密文长度增加约n倍，且只能用一次性签名检查客户和服务器的有效性，不能实现显式双向认证。分析并与表2相比文献[13]的客户计算复杂度与通信开销比本文方案的要大，协议效率低。

文献[18]是格上高效的2PAKE协议，且需通信数为3轮，分析并与文献[13]相比，客户端用CPA安全的公钥加密口令，降低公钥尺寸和密文长度，提高协议效率。协议第2轮中，客户端通过CCA安全的公钥加密体制重复加密密文实现对服务器的显式认证，与本文协议相比，增加了客户端的计算复杂度，协议中哈希函数的计算较多。分析并与表2相比本协议降低客户计算复杂度，提高协议的效率。

文献[20]是格上应用可分离公钥加密构造2PAKE协议，需要通信数为2轮，虽然降低通信轮数，但可分离的公钥加密体系和非交互式零知识证明的复杂代数关系，使得该方案的通信开销度增加，协议效率降低。

文献[22]是基于LWE困难问题的强安全AKE，协议，仅需要2轮通信，没有任何加密原语来实现身份认证，协议极其简单。与本文协议相比，尽管计算复杂度低、效率高，但该协议不能实现双向认证，且适用于特定场合的应用程序，局限性大。

4 结束语

本文将具有近似平滑投射性的CPA安全的PKE′体制和带有标签的CCA安全的PKE体制相结合，设计了格上新的2PAKE协议。该协议通过平滑投射哈希函数的正确性，利用伪随机函数簇计算认证值，在后量子时代中具有及其重要的意义。在客户端用CPA安全的PKE′体制加密口令，降低公钥尺寸和密文长度；用计算伪随机函数的值替换重复加密口令计算认证值实现对服务器的认证，降低计算复杂度，提高协议的运行效率；与已有的同类协议相比较，该协议具有描述简单，计算复杂度低等优势，同时协议的两方参与者都实现了显式相互认证，可抗量子攻击，并给出其安全证明。