浅谈高中数学形成性测试卷命题——以一套期中试卷的命制为例

上海市建平中学 李传峰

上海市建平中学 张永华

高中数学测试所用到的形成性测试卷（包括周考、月考、期中考、期末考、章节考等），其测试目的主要是反馈教学情况，进而反哺教学.

因此“好”的测试卷，可以准确反映学生对各知识点掌握的程度，评估学生的数学能力（数学核心素养），评价教师教学的效果，发现教师教学中的不足（学生学习中的不足）.

笔者以不久前的高二第一学期期中数学试卷（C层）为例.

命题内容：极限与无穷等比数列各项和、向量、矩阵与行列式、直线与线性规划.

考试对象：高二年级C层315名同学.

学情介绍：C层的同学数学学习的基础和能力较好.

试卷基本情况：试卷类型是笔试，试卷长度21题（填空题12道，选择题4道，解答题5道），试卷满分100分，测试时间90分钟.

期望通过率（合格率）达到0.8，期望优良率0.3左右，期望平均分71分左右.

笔者以为，一套好的数学形成性测试卷至少要考虑以下四个方面：知识点、难度、试题创新度、数学核心素养考查.

一、知识点

该指标包含两个方面：

1.知识点的覆盖率是否全面

知识点覆盖率是非常重要的指标，虽然不可能达到百分之百，但笔者以为即使是考查范围比较广的期末考试，基本知识点的覆盖率也不应低于70%.

本次命题，课程标准中的19个知识点试卷中考到了17个，知识点的覆盖率约为90%.

2.知识点在试卷中的分布是否合理

课程标准中对不同知识点的难度要求在试卷中是否合理呈现，重点知识的考查是否到位.

如何在命题中落实这些指标，笔者认为要用好双向细目表.（1）通过双向细目表确定本次考查的重点知识；（2）通过双向细目表选择合适的题型来落实各个知识点的考查.

本次命题，笔者依据课程标准的要求确定考试的重点是直线部分，难点是向量部分，填空题的11、12题和解答题的21题均以直线和向量为背景，把重点和难点的考查落实到位.

二、难度

1.形成性测试试卷难度的一般原则

关于本次试卷的总体难度，笔者确立了三条原则：（1）期望平均分71分左右；（2）及格率在0.80-0.90之间；（3）尽可能不出现满分.

经过多年的命题反馈，笔者发现满足这三条原则的试卷有以下好处：

（1）成绩区分度较好；（2）可以较好地反馈教师教和学生学的真实情况；（3）有利于激发学生学习数学的热情（学困生和学优生都容易得到激励）.

本次考试的结果（统计人数315人）：最低分43，最高分97，平均分73分，及格率0.86，优秀率（85分及以上）0.13.

2.调控试卷难度的几点建议

要想命制一套整体难度合理的试卷，需要注意以下几点.

（1）教师在平时教学中通过学生的课堂反应和作业质量对学生学习的情况进行较准确的评估.

（2）命题时要认真考虑以下三点：①考查内容的多少和难度；②学生是否充分复习；③认真预测每一题的难度，从而获得试卷整体难度的预测.

（3）先命压轴题，再根据压轴题的难度确定其他题目难度.

三、试题创新度

试卷的题目来源有三类：陈题、改编题、原创题.

笔者在命卷时，基础题多用陈题或改编题，而较难的题目多用改编题和原创题.特别是压轴题（填空题最后两道，解答题最后一道）是原创题.这种设置既有利于提高试卷的效度，又有利于提高试卷的信度.

本次考试笔者编制了三道原创题.（注：题号均为原试卷中的题号）

11.在向量a=（x，y）的右边乘以一个矩阵A2×2，按向量的乘法规则相乘以后得到一个新的向量a0，我们把这个运算过程称为对向量a实施了一次右矩阵变换.直线l1：y=ax+2上任意一点P（x，y）确定向量通过矩阵对向量实施右矩阵变换后得到向量，点P1的坐标（x0，y0）满足y0=3x0-b，若直线l2：a1x+b1y+1=0和l3：a2x+b2y+1=0相交于点T（3a，b），则过点E（a1，b1），F（a2，b2）的直线l4的方程是______.

参考答案：x+6y+1=0.

命题说明：本题分三段，第一段学生通过阅读学习“右矩阵变换”的概念，运用右矩阵变换完成由向量（x，y）到向量（y，x）的“对称变换”；第二段的运算形式上是考查“直线关于直线对称”，实质上笔者的意图是把直线的知识点与高一上学期学习的有关函数的知识点进行联系和整合，此处实质上是一次函数y=ax+2与y=3x-b互为反函数，因此通过反函数运算更简单，通过这种设计，丰富运算能力考查的层次性；第三段主要是考查思维能力，看学生对直线方程的理解是否达到一定高度.通过综合三个知识点从而提高题目的难度，既考查学生基础知识和基本方法的掌握，又考查学生数学运算和数据分析的素养.

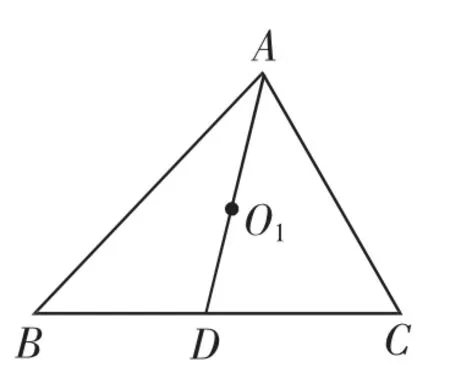
图1

12.如图1，△ABC中，BC=1，D为BC的中点，AD=1，O1为AD的中点，取线段DO1的中点O2，线段的DO2的中点O3，线段的DO3的中点O4，…，线段DOn-1的中点On（n为大于1的自然数），令ti=n），当n→∞时，数列{tn}的各项和等于______.

命题说明：

涉及知识点：向量平行四边形法则、三角形法则、等比数列、无穷等比数列各项和公式.

数学核心素养考查：数学抽象和直观想象.

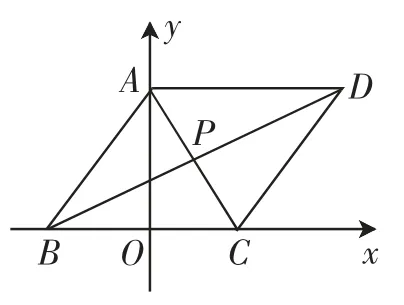
图2

（1）求直线CD的方程；

（2）若点E，F分别在平行四边形ABCD的边BC和CD上运动，且EF∥BD，求的取值范围；

（3）试写出三角形PCD区域（包括边界）所满足的线性约束条件，若在该区域上任取一点M，使，试求λ+μ的取值范围.

命题说明：

涉及知识点：直线方程、向量的坐标运算、二次函数、平面向量分解定理、线性规划.

数学核心素养考查：数学建模.

四、数学核心素养考查

文学中的小说有所谓的明线（索）和暗线（索），其实命数学试卷和写小说一样，也有明线索——数学知识点的考查，和暗线索——数学核心素养（数学方法和能力）的考查，除了在双向细目表中列出每题要考查的知识点，笔者喜欢如文2和文3那样把每一道题所要考查的数学核心素养（数学方法和能力）也列出来，这样等整张试卷出好以后，可以从整体上分析明线——基础知识考查和暗线——数学核心素养（数学方法和能力）考查，从而整体判断本张测试卷的知识覆盖率和数学核心素养（数学方法和能力）覆盖率.

五、结束语

笔者所在学校对测试卷的命题质量有一套评价标准，虽然不一定非常科学，但体现了对命题评价的重视和有益探索.评价内容分四个方面：试卷创新度、试卷达成度、试卷知识点覆盖率和试卷勘误率，每一个评价方面再细化出操作细则.

当然，由于学生差异、教材差异和学校差异，具体用什么样的标准来评价试卷，还需要各位教育同仁根据各自的实际情况进行探索.