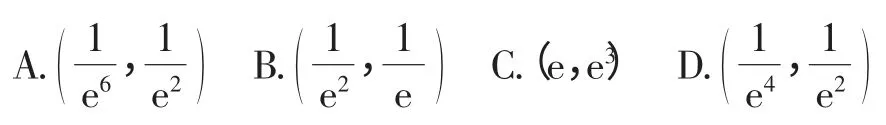追根溯源，巧妙构造辅助函数解选择压轴题

广东省广州市天河中学 王翠娜

全国高考选择题大多以函数压轴.近两年来，随着使用全国卷的省份越来越多，我们不难发现，选择题中以函数的导数为工具，利用函数的单调性解不等式或比较大小或求取值范围的压轴题已经成为各地模拟题的热点.但是这类题目需要学生有敏锐的数学观察能力和熟练的代数变形能力，成为学生学习和考试的难点.只有抓住问题的本质特征，才能从根本上解决问题.随着新课程标准的实施，高考越来越重视考查学生的数学思维能力和核心素养，这更需要我们追根溯源，回归根本.本文以微专题的形式谈一谈如何构造辅助函数解决问题.请看下面的题目：

1.（2018届天河区一模理）设函数f（x）在R上存在导数f′（x），∀x∈R，有f（-x）+f（x）=x2；当x∈（0，+∞）时，f′（x）＜x；若f（4-m）-f（m）≥8-4m，则实数m的取值范围为（ ）.

A.［-2，2］ B.［2，+∞）

C.［0，+∞） D.（-∞，-2］∪［2，+∞）

2.（2018届天河区二模理）已知定义在（0，+∞）上的函数f（x），满足：（1）f（x）＞0；（2）2f（x）＜f ′（x）＜3f（x）（其中f ′（x）是f（x）的导函数），则的取值范围为（ ）.

第1题我校平均分为1.532，难度系数为0.307，第2题我校平均分为2.312，难度系数为0.4089.经过了一个学期的复习，这样的题目也做过不少，平均分并没有提高多少，况且里边还存在一些同学碰运气猜对的情况，真正会做的就更少了.根本原因是学生没有抓住最本质的东西，不知道从哪里下手构造函数，甚至完全没有思路.此类题的解题技巧是构造辅助函数，利用辅助函数的单调性、奇偶性，实现问题的转化，从而使问题得到解决.而如何根据条件的结构特征构造一个可导函数是解决这类问题的关键.这也是全国高考题对能力考查的创新，本质上是视角的转换.我们的复习就是要用创新应对创新，用转换适应转换.在试题创新背后，一定存在着稳定的东西.备考者要沿着命题者的思路回到原点，感受知识到能力的过程，把隐性的解题经验显性化、算法化.本文以探求最本质的根源，寻找最一般的解题思路为出发点，追根溯源，回归根本.

一、追根溯源（基本导数公式）

公式1：设F（x）=f（x）±g（x），则F′（x）=f′（x）±g′（x）.

公式2：设F（x）=f（x）·g（x），

则F′（x）=f ′（x）·g（x）+f（x）·g′（x）.

公式4：设F（x）=xf（x），则F′（x）=f（x）+xf′（x）.

公式6：设F（x）=xn·f（x），

则F′（x）=nxn-1f（x）+xn·f′（x）=xn-1［nf（x）+xf′（x）］.

公式8：设F（x）=ex·f（x），则F′（x）=ex［f（x）+f′（x）］.

二、变形拓展（规律总结）

1.若已知条件为f（x）+f′（x）的“加”型结构：

（1）f′（x）+g′（x）≥0，构造函数F（x）=f（x）+g（x）.

（2）f ′（x）·g（x）+f（x）·g′（x）≥0，构造函数F（x）=f（x）·g（x）.

（3）f（x）+f′（x）≥0，构造函数F（x）=exf（x），［exf（x）］′=ex［f（x）+f′（x）］.

（4）f（x）+xf′（x）≥0，构造函数F（x）=xf（x），［xf（x）］′=f（x）+xf′（x）.

（5）xf′（x）+nf（x）≥0，构造函数F（x）=xn·f（x），［xn·f（x）］′=nxn-1f（x）+xn·f′（x）=xn-1［nf（x）+xf′（x）］.

2.若已知条件为f（x）-f′（x）的“减”型结构：

（1）f′（x）-g′（x）≥0，构造函数F（x）=f（x）-g（x）.

（2）f′（x）g（x）-f（x）g′（x）＞0，构造函数

以上是常用的构造技巧，但具体还要联系已知条件和结论，结合f（x）和f′（x）的关系式，以及根据不等式的“形状”适当变形来选择构造形式.但一定要明确题目给出的f′（x）的关系式，这是我们要构造的函数导数中的一个因式，我们就是根据这个来思考问题的.请看下面几个例子.

例1 定义在R上的可导函数f（x），其导函数f′（x）满足f′（x）＞2x恒成立，则不等式f（4-x）+8x＜f（x）+16的解集为（ ）.

A.（2，+∞） B.（4，+∞）

C.（-∞，2） D.（-∞，4）

解析：学生不知道条件f ′（x）＞2x怎么用.其实根据f ′（x）＞2x，可构造函数g（x）=f（x）-x2，则g′（x）=f′（x）-2x＞0，g（x）在R上单调递增.

g（4-x）=f（4-x）-（4-x）2=f（4-x）-16+8x-x2，所以不等式f（4-x）+8x＜f（x）+16⇔g（4-x）+16+x2＜f（x）+16⇔g（4-x）＜f（x）-x2=g（x）⇔4-x＜x，从而得解.特别注意求解的不等式与构造的辅助函数之间的关系.

例2 （2007年陕西卷理）已知f（x）是（0，+∞）上的非负可导函数，且xf ′（x）-f（x）≤0，对任意正数a，b，若a＜b，则（ ）.

A.bf（a）≤af（b） B.af（b）≤bf（a）

C.af（a）≤f（b） D.bf（b）≤f（a）

例3 已知定义在R 上的可导函数f（x）的导函数为f′（x），满足f′（x）

A.（-2，+∞）B.（0，+∞）C.（1，+∞）D.（4，+∞）

例4 函数f（x）的定义域为（0，+∞），其导数为f′（x），且满足f（x）>0，f（x）

解析：处理本题的关键是合理利用f（x）

例5 设函数f ′（x）是函数f（x）（x∈R）的导函数，f（0）=1，且3f（x）=f ′（x）-3，则4f（x）>f ′（x）的解集为（ ）.

解析：利用“减”型结构里的公式6，这里m=1，n=3，f ′（x）=3［f（x）+1］.构造函数g（x）=，所以g（x）为一个常数函数，且g（0）==2，所以g（x）=，即f（x）=2e3x-1，f′（x）=6e3x.因为4f（x）>f′（x），所以4（2e3x-1）>6e3x.所以e3x>2.所以lne3x>ln2，所以x>.故选B.

复习时可以采用微专题的形式，让学生先从几个简单题入手，直接套公式，构造法的原理先掌握住，再灵活变形迁移，由易到难，思维提升，可以很好地提高学生的数学思维能力，取得较好的复习效果.

例6 已知奇函数f（x）的定义域为（-∞，0）∪（0，+∞），f′（x）为其导函数，且满足以下条件：

以上几题构造函数的过程，遵循高中数学课程标准的基本理念“倡导积极主动，勇于探索的学习方式”，可以让学生对照公式自己构造出来，“让学生体验数学发现和创造的历程，发展他们的创新意识”.这几题会做了，天河区一模和二模的题自然就不是问题了.从题目中“提炼”出反映数学本质的东西，从数学本质上思考，我们才能品味到它们的必然性！当学生看到类似的题目时，能有一种“一览众山小”的感觉，那么我们的复习就成功了.