高考数学答题谨防五误区

江苏省宜兴市和桥高级中学 王 蓬

新课标高考中起决定性作用的往往是数学，基于数学这门课的考试特点，一个客观题就是5分，而一个主观题占14至16分，考生在考试时稍有疏忽，答案就会出现“失之毫厘，谬以千里”的现象.那么，在高考数学答题中有哪些误区需要特别关注呢？

一、审题不清

每次考完试后，总有一部分考生会槌胸蹋地，懊悔不已，因审题失误丢了不少分.有些考生自以为客观题简单，考试时往往对其采用“一目十行”的快速阅读方式，自以为抢得了时间，结果是要么看错题意，要么忽视题目中的附加条件，更有甚者，虽把准确答案做出，却没按照要求填写.

例1 设l，m表示直线，m是平面α内的任意一条直线，则“l⊥m”是“l⊥α”成立的______条件（选填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”）.

错解：必要不充分.

剖析：本题错误率极高，多数考生看完题目后立即想到直线与平面垂直的判定定理，即α，却根本没有注意到题目中已经告知直线m具有任意性，于是把答案错误地写成“必要不充分”.事实上，解答这道题，只需依据课本对线面垂直这个概念的定义，就可得到正确答案：充要.可见审题不是凭空而起，必须联系课本知识.

正解：充要.

点评：审题是解题的重要组成部分，也是正确解题的保障.所谓审题，就是要求我们看清题目条件，弄清解答要求，通过主观的分析与判断，选择恰当的解题方法，设计合理的解题步骤.数学审题，其实就是对数学语言的识别，如何实现条件与结论之间的转换，这就要求我们通过阅读题意分析题意，去揭示题目中数与数、形与形和数与形之间的本质联系.

二、有关概念与定理认识不清

数学答题的理论依据就是课本上的有关概念与定理，答题时，必须对课本上所有的概念、定理和性质了如指掌，否则很难把题目做对.

例2 已知等差数列{an}中，若a3+a4+a5+a6+a7=450，则a2+a8=______.

错解：因为a3+a7=a10，a4+a6=a10，2a5=a10，

因为a2+a8=a10，所以a2+a8=180.

剖析：上述过程似乎有道理，但缺乏根据，结果纯属巧合，不可取.实际上，在等差数列{an}中，当m+n=p+q时，才有am+an=ap+aq成立.注意：等式两边均为两项.

正解：因为a3+a7=2a5且a4+a6=2a5，

所以由a3+a4+a5+a6+a7=450得5a5=450.所以a5=90.

又a2+a8=2a5，所以a2+a8=2×90=180.

点评：高考复习不可脱离课本，我们应该重视对数学概念和有关定理、性质和公式的复习.对数学概念、定理、性质和公式的理解，不可仅仅局限于字面上，而应该对其内涵进行加工，不仅要学会从正面理解它们，还要能举出反例，突破理解盲区.例如大家在复习等比数列概念时，我们不仅要弄清通项、首项、项数及公比之间的内在关系，还要不断总结等比数列中的易错点.

三、思维定式

思维定式，有时也会“害死人”.有的考生看见与平时遇到的题目相类似，往往凭解题经验，马上动笔，结果解答出错.有的考生则陷入欲进不能、欲罢不能的困境，白白浪费了珍贵的考试时间.

例3 如果x，y∈R+且满足x+2y=4，那么的最小值为______.

以上代数式十分烦琐，无法通过基本不等式凑出定值，于是不了了之.

剖析：造成上述错解的原因是受到了陈题“如果x，y∈R+且满足x+2y=4，那么的最小值为______”的解题方法的约束，没能及时调整解题策略.

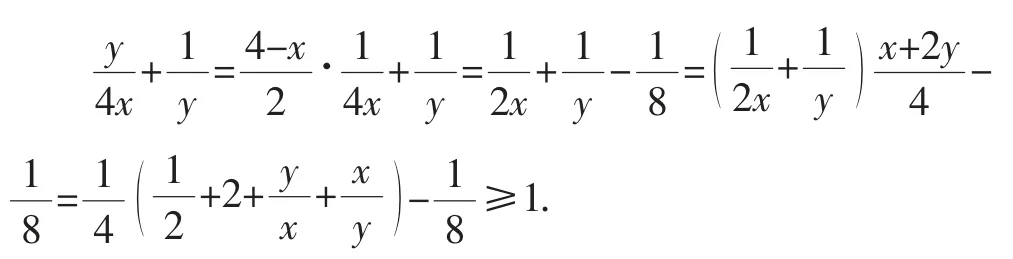
点评：墨守成规，不善创新，是高考答题的禁忌.我们平时解题，要养成打破常规，乐于创新的思维习惯.在解题中善于发现题目中的“不一样”，用不一样的解题方法，去攻破不一样的题目.只有这样，才能摆脱题海，回头是岸.

四、答题不规范

考场答题，规范第一.但有些考生却做不到这一点，喜欢随心所欲，一旦写错，就涂涂改改，卷面十分不整洁，甚至令阅卷老师无法找出答案，从而影响到阅卷的判分.有些考生喜欢跳步答题，缺少必要步骤，如解答最后不写总结，虽然自我感觉都做对了，但由于不合解题规范，照样被扣分，十分可惜.

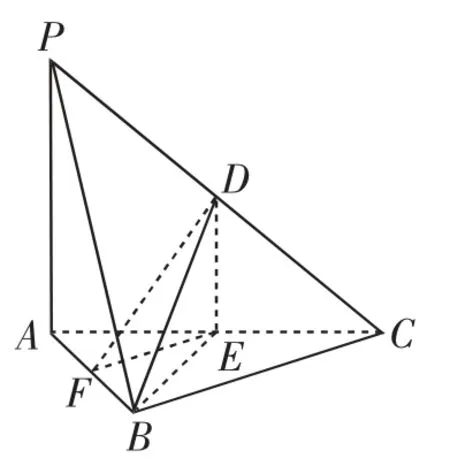
图1

例4 如图1，在三棱锥PABC中，D，E，F分别为棱PC，AC，AB的中点.已知PA⊥AC，PA=6，BC=8，DF=5.

求证：（1）直线PA∥平面DEF；

（2）平面BDE⊥平面ABC.

不规范解答：

（1）因为D，E分别为棱PC，AC的中点，所以DE∥PA.

所以直线PA∥平面DEF.

（2）因为D，E，F分别为棱PC，AC，AB的中点，PA=6，BC=8，所以DE∥PA，DE=PA=3，EF=BC=4.

又因为DF=5，故DF2=DE2+EF2.

所以∠DEF=90°，即DE⊥EF.

又PA⊥AC，DE∥PA，所以DE⊥AC.

所以DE⊥平面ABC.

所以平面BDE⊥平面ABC.

剖析：上述证明过程，若不仔细推敲，则往往认为可以得满分.可细心斟酌，却会发现，在应用有关判定定理时，漏写了必须写的条件，如，用线面平行判定定理时，必须写明直线所在的位置；用线面垂直判定定理时，必须交代平面内的两直线相交.

点评：高考阅卷判分，既重视结果，更看重过程，都是按步给分的，尤其是立体几何解答题，更注重答题的规范性.所以对于会做的题目，同学们在书写过程中，一定要做到语言严谨，书写规范到位，谨防“低级错误”.

五、时间分配不科学

有些考生缺乏对自己实力的正确判断，总是希望自己能答遍试卷上所有的题目，于是“来也匆匆，去也匆匆”，匆忙答题只能造成漏洞百出的后果.虽然从卷面上看，写得头头是道，但却得不了几分.其实高考是一场选拔性考试，我们不求最好，但求更好.对此，我们必须科学合理地分配好答题时间，有把握的题目应力争得满分，对于没有把握的题目果断放弃.只有这样，才能提高考场得分效率.

例5 不等式ax2+x-2a＜0是一个关于x的二次不等式，如果它的解集里只含有4个整数，那么实数a的取值范围是______.

本题是填空题的压轴题，具有一定的难度，若考生没有一定的数学素养和转化能力，即使花上两个小时也不一定能做出来.我们必须知道，这道题的“性价比”其实并不高，同第一个填空题一样，也只有5分，当思路不明晰时，我们大可不必在此类问题上浪费时间.

本题详解：由题意可知：a＞0，令f（x）=ax2+x-2a，则f（0）=-2a＜0，此时需要讨论f（-1）=-1-a＜0，f（1）=1-a不能确定其正负.再来计算f（-2）=2a-2=2（a-1），f（1）f（-2）≤0.下面对a进行讨论：

（1）a=1时，f（1）=f（-2）=0，则不等式ax2+x-2a＜0的解集中仅有2个整数解0和-1，不符合题意.

（2）a＞1时，f（1）＜0，f（-2）＞0，f（2）=2a+2＞0，此时整数解有3个，分别为0，1和-1；不符合题意.

（3）a＜1时，f（1）＞0，f（-2）＜0要使不等式有4个整数解必须满足：

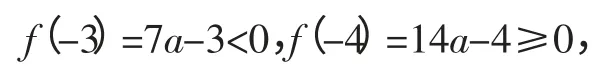
点评：基础题和中档题是大多数考生的主要得分点，大多数考生考试时的主要精力要用在这些题上.那些难题对不少考生来说，即使带回家也不一定做得出来，因此要“学会放弃”，有所不为才能有所为.在试卷发下来后，我们应通览全卷，把握“题情”，分清哪些是基础题，哪些是中档题，哪些是难题，初步确定对应的作答时间，从而让每一分钟都能产生答题效益.

常言道：考场如战场.避免失误，就是得分最有效的途径.因此，我们不仅要训练数学解题技能，也要训练稳如泰山的考试心理素质.