几种常见的三角函数求值方法的总结*

海口市琼山华侨中学 李 武

三角函数求值是高中数学的重要内容，高考中经常考查三角函数求值问题.在近几年的高考命题中，三角函数的求值一般是以选择题和填空题的形式出现，而学生在解决此类问题时常常不能快速针对题目特点选择相应的解题方法.为了便于学生复习三角函数求值问题，本文将三角函数中常见的几种问题给出相应的解题方法.

一、三角函数定义求值法

在三角函数求值问题中最基本的一种求值是已知tanα、sinα、cosα中的某一个三角函数值，求另外一个三角函数值，可选用定义法解题.

分析：由已知条件可知，解决此问题可以直接通过定义法或者利用三角函数的基本公式进行解题.

注意：当遇到一些特殊角的三角函数值时，可以先根据题意得到角再求值而不需要用定义法求值.

二、未知角由已知角表示求值法

定义1：若题目中要对某个角求三角函数值，则称该角为未知角.

定义2：将题目中已给出的某个角的函数值，以及能得到函数值的特殊角统称为已知角.

类型1：已知条件只给出一个角的三角函数值，当未知角和已知角消去参量α后得到一个特殊角则可用此法.

分析：因为2α-2（α-π）=2π，所以2α=2π+2（α-π）.而2π是个特殊角，所以可用此法.

解：cos2α=cos［2π+2（α-π）］=cos2（α-π）=1-

类型2：若条件给出两个角的三角函数值，则未知角通常可由已知角线性表示.

三、构造tan型求值法

定义3：三角函数分式指的是分子分母中都含有三角函数.

定义4：三角函数整式指的是式子中分母不能含有三角函数.

类型1：已知条件给出tanα的值或者给出一个三角函数分式的值，求tanα的值或是求三角函数分式的值时，则可考虑用构造tan型，但要注意三角函数分式中的分子和分母每一项必须要同次幂.

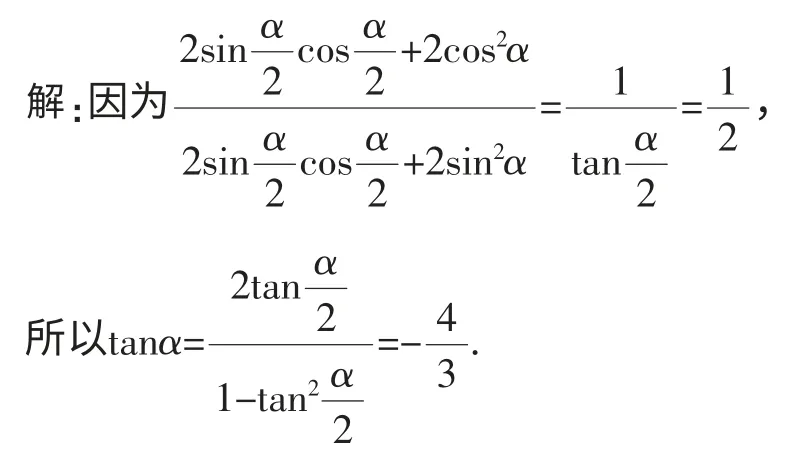
类型2：已知条件给出一个三角函数整式的值，求tanα、三角函数分式或整式的值则可考虑用构造tan型求值，但要注意三角函数整式要转化成分式并且要求三角函数分式中的分子和分母每一项必须要同幂.

例6 已知sin2α+3cos2α=2.

（1）求tanα的值；

分析：sin2α+3cos2α=2是个三角函数整式方程，所以根据类型2的条件先将三角函数整式化为分式并要求分式中分子分母的每一项要同幂.

即tan2α=1，

解得tanα=±1.

（2）由（1）可得tanα=±1.

所以当tanα=1时，原式=0；

当tanα=-1时，原式=2.

类型3：已知条件给出一个三角函数整式的值但当将整式转变为分式后分子分母每一项不能同幂，此时就先考虑将已知的整式升幂使得分子分母每项同幂再进行解题.

解得tanα=7或tanα=1.

从多个角度对三角函数求值进行探索处理，总结归纳题目特点，巧妙地把此类题目的底蕴充分挖掘出来，从多角度出发，多方面求解，多层次拓展，体现了数学从探索到解决问题的技能.W