在变形与观察中联系通性通法
——对一类压轴试题的教学思考
2019-12-26湖北省十堰东风高级中学黄祥兵
湖北省十堰东风高级中学 黄祥兵
湖北省十堰市教育科学研究院 程世平
数学教学离不开解题,解题教学是数学教学的重要组成部分,提高学生的解题能力也是提高学生数学核心素养的重要途径.各种考试的压轴试题通常设计的思维层次较高,运算也较复杂,如何使学生在压轴试题的解题上有所突破,如何使学生在解压轴题时能有章可循,是我们在习题教学中需要重点解决的问题.下面就一类压轴题谈谈如何通过变形与观察把复杂的数学问题与我们所熟知的通性通法有机地结合起来,让学生在变中求进、进中求通,用常规方法解决高难度的数学问题.
例1 (高三五月联考题)已知函数f(x)=(ex-1)(xb),F(x)=x3+mx2+nx-2,若曲线f(x)在点(1,f(1))处的切线方程是y=(e-1)(x-1),不等式F′(x)+3<0的解集为非空集合其中e为自然对数的底数.
(Ⅰ)求f(x)的解析式,并用a表示m,n;
(Ⅱ)若对任意x≥0,不等式2f′(x)≥F(x)恒成立,求实数a的取值范围.
解法一:(Ⅰ)略.
(Ⅱ)由(Ⅰ)可得F(x)=x3-2ax2+(a2-3)x-2,由f′(x)=xex-1得2f′(x)≥F(x)⇔x[2ex-(x-a)2+3]≥0,由非空集合得a<0.
令g(x)=2ex-(x-a)2+3,则g′(x)=2(ex-x+a),又令h(x)=2(ex-x+a),则有h′(x)=2(ex-1)≥0,所以h(x)在[0,+∞)上为增函数,且h(x)min=h(0)=2(a+1).
①当-1≤a<0时,h(0)≥0,g′(x)≥0恒成立,即g(x)在[0,+∞)上为增函数,则有g(x)≥g(0)=5-a2≥0,得,结合-1≤a<0得-1≤a<0.
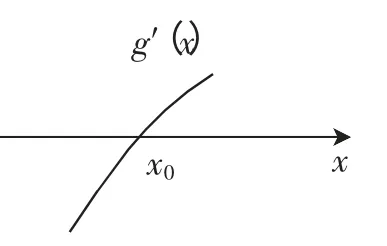
图1
②当a<-1时,则∃x0>0,使h(x0)=0且x∈(0,x0)时,h(x)<0,即g′(x)<0,即g(x)在(0,x0)上单调递减;x∈(x0,+∞)时,h(x)>0,即g′(x)>0,即g(x)在(x0,+∞)上单调递增,所以g(x)min=g(x0).所以只需满足g(x0)=2ex0-(x0-a)2+3≥0.又h(x0)=2(ex0-x0+a)=0,从而2ex0-(ex0)2+3≥0,解得0<x0≤ln3,由ex0-x0+a=0⇒a=x0-ex0,令M(x)=x-ex,0<x≤ln3,M′(x)=1-ex<0,所以M(x)在(0,ln3]上单调递减,则M(ln3)≤M(x)<M(0),即ln3-3≤M(x)<-1,故ln3-3≤a<-1.
由①②可知a的取值范围为[ln3-3,0).
解法分析:(1)本解法用到了分类讨论的数学思想,逻辑清晰、层次清楚,但整个过程对学生的综合能力要求较高,在分类讨论的基础上利用了二次求导和整体代换.
(2)分类讨论凸显了思维的严谨性,但很容易出错,在利用导数解决问题的过程中,涉及选择新变量,构造新函数,再以导数为工具求a的取值范围.
(3)整个讨论围绕着求函数g(x)=2ex-(x-a)2+3的最小值.
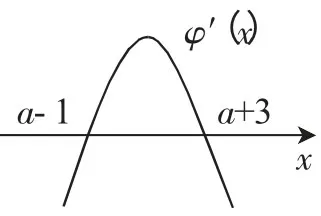
图2
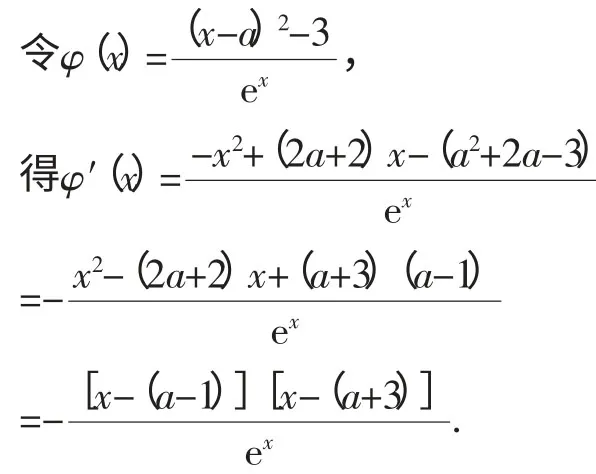
①当a+3<0,即a<-3时,x∈[0,+∞)时,φ′(x)≤0,函数φ(x)在[0,+∞)上为减函数,
所以φ(x)max=φ(0)=,解得与a<-3矛盾,此时a∈Ø;
②当a+3≥0,即a≥-3时,x∈[0,a+3]时,φ′(x)≥0,函数φ(x)在[0,a+3]上为增函数,x∈[a+3,+∞)时,φ′(x)≤0,函数φ(x)在[a+3,+∞)上为减函数,所以φ(x)max=φ(a+3)≤2,解得ln3-3≤a<0满足a≥-3,即ln3-3≤a<0.
由①②可知a的取值范围为[ln3-3,0).
(2)模式很重要,解题中若出现f′(x)+f(x)自然会联想到ex·f(x);若出现f′(x)-f(x)自然会联想到;若出现xf′(x)+f(x)自然会联想到xf(x);若出现xf′(x)-f(x)自然会联想到等.
(3)方法很重要,解题中若出现恒成立的问题,自然会结合变量分离,只是怎样分离变量,本题中就是变形成的形式来进行类似于变量的分离,本解法就是通过变形来联系通性通法.
例2 (2019年全国卷)已知函数f(x)=sinx-ln(1+x),f ′(x)为f(x)的导数.证明:
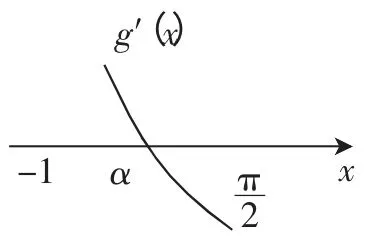
图3
(Ⅱ)f(x)有且仅有2个零点.
证明:(Ⅰ)设g(x)=f′(x),
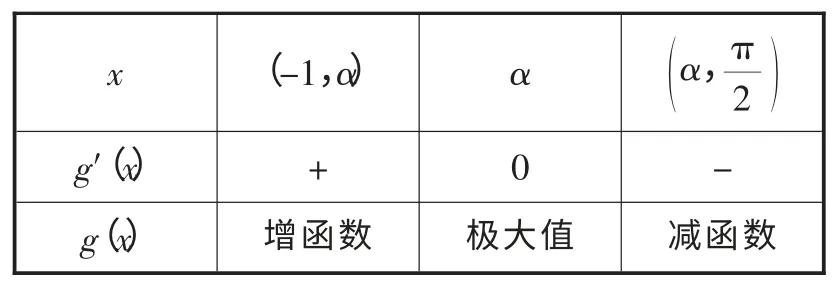
(Ⅱ)f(x)的定义域为(-1,+∞).
①当x∈(-1,0]时,由(Ⅰ)知,f ′(x)在(-1,0)上单调递增,而f ′(0)=0,所以当x∈(-1,0)时,f ′(x)<0.故f(x)在(-1,0)上单调递减,又f(0)=0,从而x=0是f(x)在(-1,0]的唯一零点.
④当x∈(π,+∞)时,ln(x+1)>1,所以f(x)<0,从而f(x)在(π,+∞)上没有零点.综上所述,f(x)有且仅有2个零点.
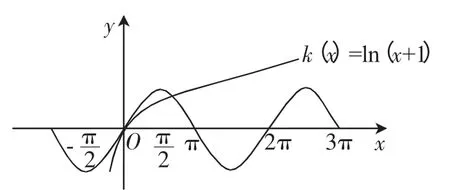
图4
解法分析:(1)本题为2019年全国卷Ⅰ的第20题,该题设计新颖,考查学生灵活利用函数导数知识解决问题的能力.
(2)第二问分类讨论,情况较多,标准要求清晰,难度较大,分四种情况是根据数形结合的思想方法对问题的严谨分析推理,具体的分析过程是:在同一坐标系内作出h(x)=sinx和k(x)=ln(x+1)的简图,(0,0)是两函数的一个交点,且k(e-1)=1,那么若f(x)有且仅有2个零点,则意味着f(x)在x∈(-1,0),x∈上没有零点,x∈时f(x)有一个零点,这样的分析就是我们分四类讨论的依据.
(3)基于以上结合图形的分析,我们证明问题的步骤才会清晰明了.
一道好的数学试题一定会强化通性通法,淡化特殊技巧,并且不偏不怪,考查学生思维的灵活性和对数学知识和方法的熟练应用,以上例1是衡水中学的5月联考题,解法一是常规解法,分类讨论求函数的最小值,然后研究新函数,求a的取值范围;解法二是我们重点强调的,通过变形与观察转化成求的最小值问题,而是我们需要重点掌握的函数模型,它的导数与0的大小关系通常可以转化为多项式函数与0的大小关系,而多项式函数是我们所熟知的函数,那么这一复杂的数学问题就转化为了我们熟知的函数模型,数学中很多与ex有关的问题都可以这样去转化;例2是2019年的高考试题,学生普遍觉得很难,难在不知道零点到底在哪里?若学生有意识地把零点问题转化为函数图像的交点问题,通过分析可顺利地把区间分为四段,每一段上的研究就是常规的用导数研究函数.
压轴题是拉开差距、区分学生层次的试题,题目千变万化,但不是不能应对,我们需要做的就是加强对各类问题的归纳与提炼,整合出不同的通法模型,具体解题时,学生需要通过变形与观察联系平时所研究的通法模型,因此,我们平时的教学要注重通性通法的教学,以及学生观察与转化能力的培养,提高学生的数学素养,让学生在应对复杂的数学问题时有章可循.F
