Study on the Casas-Alvero Conjecture of Univariate Polynomials
2019-12-26YangHuanyu
Yang Huanyu
(Department of Mathematics,Zhanjiang Preschool Normal College,Zhanjiang,Guangdong 524084)
Abstract:Let f(x)be a monic complex univariate polynomial with the leading coefficient is equal to 1.This paper uses the knownledge of higher algebra to prove that if f(x)has exactly two distinct roots,then f(x)is not a Casas-Alvero polynomial.The above mentioned result partly verifies the Casas-Alvero conjecture.
Key words:Casas-Alvero conjecture;polynomial of one complex variable;derivative;root
I.Introduction
(i)Background
Since 1998,when Casas-Alvero (professor of department of mathematics,university of Barcelona)proposed Casas-Alvero conjecture[1],this conjecture has been favored by mathematical scholars and has been widely applied in topology.Professor Casas-Alvero and several mathematicians are working to prove the conjecture is correct,hoping to prove it.As a result,the problem remains unresolved and is now known as the Casas-Alvero conjecture.In this paper,the Casas-Alvero conjecture of polynomial of one complex variable is discussed with the knowledge of advanced algebra.
(ii)Overseas and Domestic Research Status
In recent years,the study of Casas-Alvero polynomials by researchers is one of the hot topics in mathematics.In 2005,Diaz-Toca G.M and Gonalez-Vega L were able to prove conjecture up to 8 (published to 7),by using the re-computation method[2].
Subsequently,Von Bothmer H-C.G,Labs O,Schicho J and Van Der Woestijne C proved that the degree of this conjecture was a power of prime numbers and some other related cases[3].
Draisma J and De Jong J.P gave different proofs of the current problem and a good introduction to conjecture,by using valuation theory to prove rather than algebraic geometry[4].
(iii)The Main Content and Significance of This Paper
Set f(x)as the

polynomial of one complex variable of n (n>1)with its leading coefficient equal to 1,then set f(k)(x)(k=1,···n-1)is the k derivative of f(x).If there is a complex number α1,···,αn-1,then
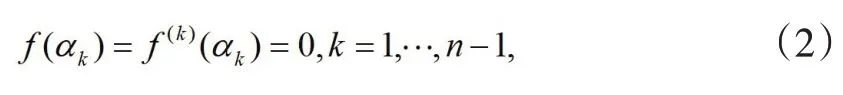
f(x)is called n-degree Casas-Alvero polynomial.In 2001,E.Asas-Alvero [1]defined this kind of polynomial when he studied the topological properties of plane curve and proposed the following conjecture:
Conjecture A If f(x)is n-degree Casas-Alvero polynomial,then there must be α is a complex number.

The above conjecture A is called casas-alvero conjecture,which is a puzzle that has not yet been solved and has only been proved in some very special cases[2~4].For example,conjecture A is true when degree n of polynomial f(x)is less than 12,but it is not known whether this conjecture is true when n=12[3].
According to the factorization theorem of complex coefficient unary polynomial,if f (x)is suitable for (3),then f (x)has the only root x=α;conversely,any polynomial with different roots cannot be represented as (3)[5].Therefore,conjecture A can be expressed equivalently as:
Conjecture B If f(x)has different roots,f(x)is not a Casas-Alvero polynomial.
It can be seen that if any polynomial with different roots can be proved not to be a Casas-Alvero polynomial,it can be concluded that the Casas-Alvero conjecture is valid.According to the above ideas,this paper solves a class of basic cases of Casas-Alvero conjecture,that is,proves the following theorem.
The primary outcome:
Theorem:If f(x)has exactly two different roots,f(x)is not a casas-alvero polynomial.
The proof of the above theorem uses the following properties of unary polynomials.
II.Some Lemma
Lemma 1[5]If the number of multiple roots is counted as multiple,then the polynomial with n degree complex coefficients has exactly n roots.
Lemma 2[5]When n degree polynomial f(x)can be expressed as(1),if α1,…,αnare the n roots of f(x),then
Lemma 3[5]The necessary and sufficient condition that x0 is the k multiple root of f(x)is that f(x0)=f'(x0)=…=f(k-1)(x0)=0,and f(k)(x0)≠0.
Lemma 4[8]Ifare all the different roots of the polynomiallike form (1),are the multiple numbers of them,thenand
Lemma 5[9]For polynomial f(x)like the form(1),let indeterminate y and x be suitable for
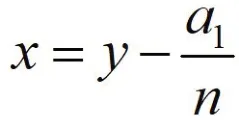
Lemma 6[5]The complex coefficient n (≥1)polynomial can be uniquely decomposed into the product of the first factor in the complex number domain.
III.Proof of Theorem
(i)Source of Ideas
The conjecture involves roots of polynomials,theory of polynomials,and n-degree derivatives of polynomials;through searching the data,it is found that the existing relevant research is extremely limited,so we can only start with the basic characteristics of polynomials and flexibly use the professional course knowledge of"advanced algebra".Fortunately,lemma 3 is very similar to the relevant conditions of the conjecture,so I choose to find a breakthrough from lemma 3 to obtain a method to prove the correctness of the conjecture.
(ii)Proof of Theorem
Set f(x)as a polynomial of n degree complex coefficients like form (1),and assuming f(x)exactly have two different roots α and β,their multiplicity is n1 and n2,respectively.At this point,α andβ are the complex numbers which are suitable for

According to lemma 1,we can know that n1 and n2 are the positive integers which are suitable for

According to lemma 2,

According to the derivation rule for unary polynomials(see[5]),the n-1-degree derivative of f(x)is
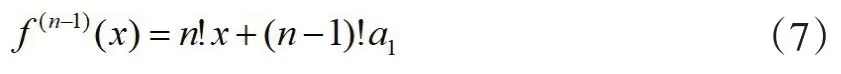
If f(x)is a Casas-Alvero polynomial,it can be known from the definition (2)of such polynomial that:there are complex number αn-1which is suitable for
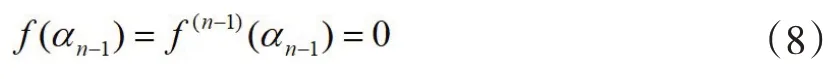
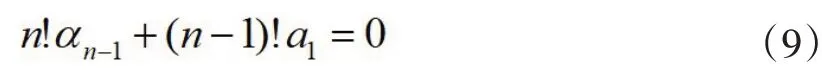
From(9),we can know that

Substitute(10)into(8),we can know that


Or

When(12)is true,it can be obtained from(6)

Combine(5)and(14),we can know that
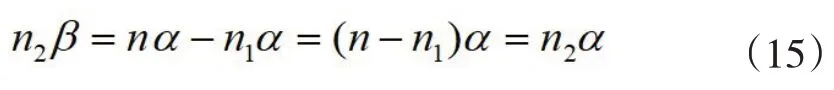
Since n2 is a positive integer,so we can conclude from(15)that α=β which contradicts(4)
Similarly,when (13)is true,the contradictory result of α=β can also be obtained.
In conclusion,it can be known that when f(x)has exactly two different roots,f(x)is not Casas-Alvero polynomial.
(iii)Application of Theorem
Example 1 Determine whether the polynomialis a Casas-Alvero polynomial.
Solution 1(elementary row operation of matrix):

Obviously,f(x)has exactly two roots of-1 and 4,so it can be directly determined from the above theorem that f(x)is not a Casas-Alvero polynomial.
Solution 2(determinant method):
Any n-degree unary polynomialcan be written as n-degree determinant

taking the characteristic of determinant,factorization is carried out by means of reduction of order and extraction of common factors[7].

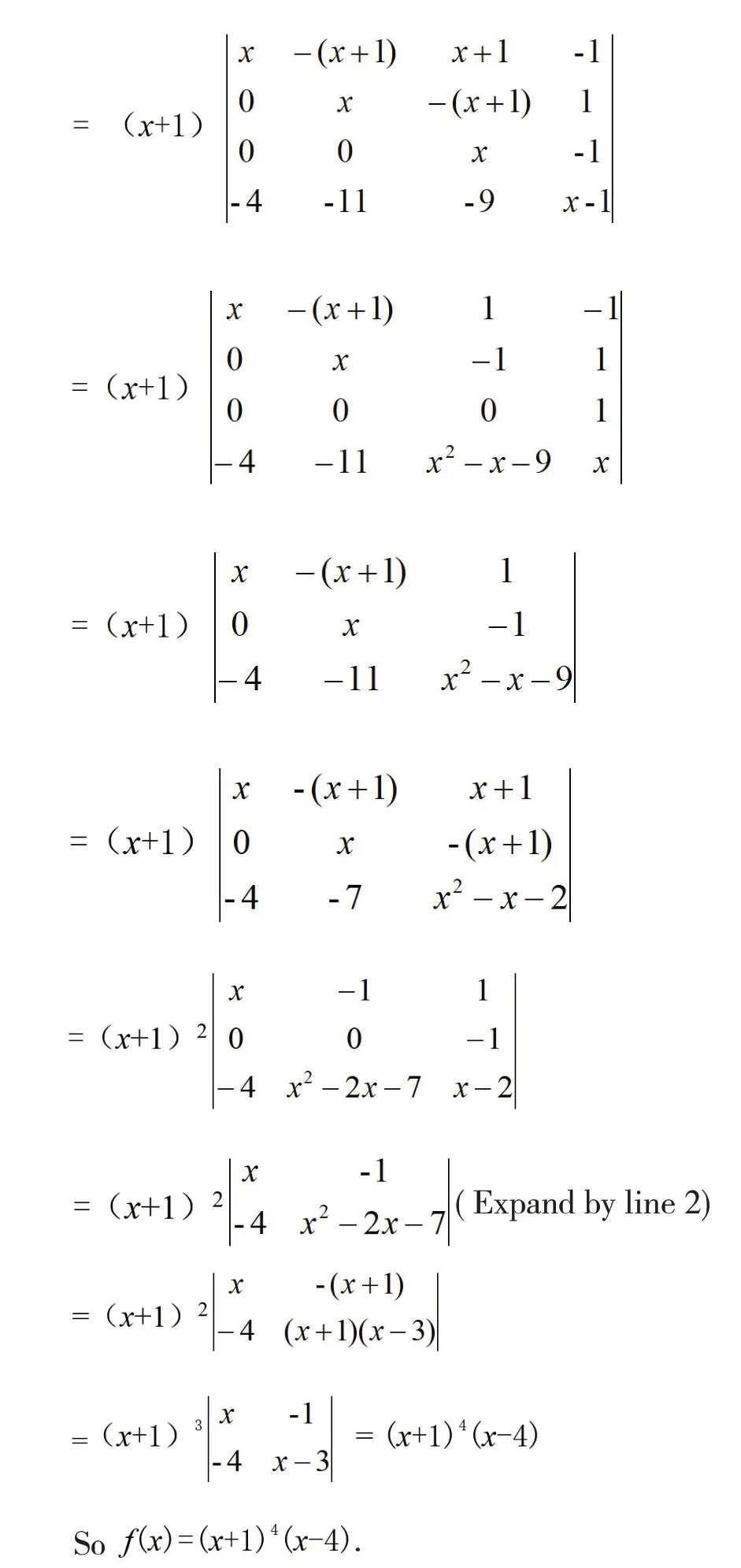
Obviously,F(x)has exactly two roots of-1 and 4.Similarly,f(x)is not a Casas-Alvero polynomial.
