Application of Computer Lingo Software in Production Efficiency
2019-12-26XiongLi
Xiong Li
(Hubei Communication Technical College,Wuhan,Hubei 430079)
Abstract:This paper comes from the problem of production efficiency when the author reads the story of mathematician,and expounds the importance of production efficiency when arranging production and the application of lingo from three aspects.
Key words:production efficiency;lingo
The author read about some books about the life and deeds of Mr.Hua luogeng,a mathematician,in spare time.Mr.Hua luogeng was the first mathematician in modern China who applied mathematical theory research to production practice and promoted the development of economic mathematics.In his later years,he vigorously promoted the unification and selection methods.
In normal production,if the way of production arrangement is different,the efficiency will be very different,here is an example to illustrate.
Suppose a factory has three workers produce two different components,in unit time,worker A can produce 80 components A or 40 components B,worker B can produce 30 components A or 90 components B,and worker C can produce 15 components A or 60 components B,each of the components is fitted into a set.So,how should the factory arrange production?
In order to facilitate the understanding,we list the key data in the above conditions as follows:
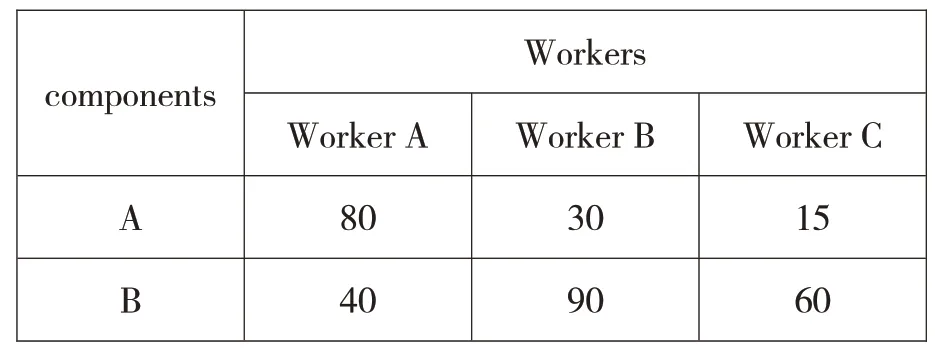
I.First of all,Suppose that Each Worker is in a Row,and Each of Them Can Produce Matching A and B Parts
If unit time is 1,worker A's time to produce part A isx,and the time to product part B is1-x,then:80x=40(1-x),solved to getx=
At this time,the production of parts componentspieces each,constituting 27 sets.
Similarly,the unit time is 1,and the time worker B spent to produce part A isy,and the time to product part B is1-y,then:30y=90(1-y),solved to gety=At this time,the production of parts componentspieces each,constituting 23 sets.
As for worker C,the time worker C spent to produce part A isz,and the time to product part B is 1-z,then 15z=60(1-z),solved to getz=At this time,the production of parts componentspieces each,constituting 12 sets.
The data list is as follows:
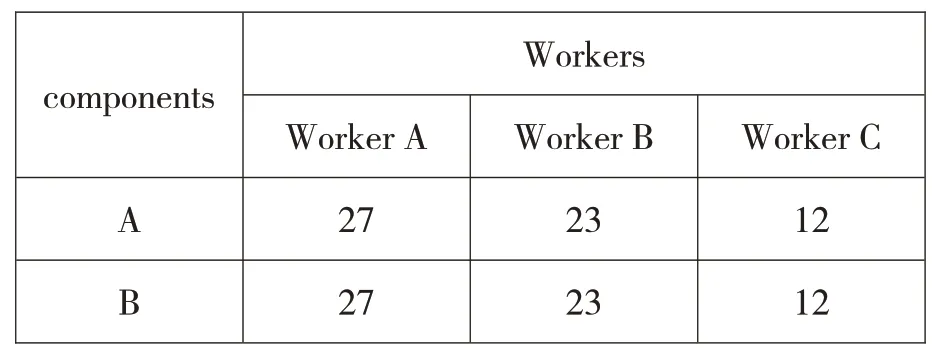
Therefore,the total number of sets of parts produced is 27+23+12=62sets.
Obviously,this method does not give full play to the advantages of each worker,the speed of A,B and C is different.Within the unit time,worker A produces the largest number of parts A and worker B produces the largest number of parts B.If the workers with the largest number of parts are arranged to produce only the parts,there are the following ways.
II.Whoever Produces More of That Parts will be Arranged to Produce that Parts
Worker A produces part A in the largest quantity within the unit time,worker A shall be arranged to produce part A;Worker B produces part B in the largest quantity within the unit time,worker B shall be arranged to produce part B;in order to match the A and B,worker C shall produce two parts.Set the time of worker C used to produce part A asx,then the time of producing part B isxx,and we can get:

Solved to getx=,the quantity of part A produced by worker C issets,the quantity of parts B produced by worker C is.The total number of parts is listed below:
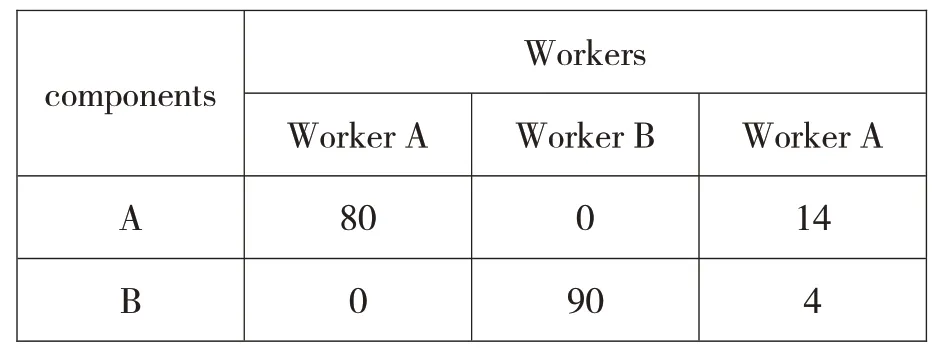
Therefore,the total number of sets of parts produced is 80+14=90+4=94sets.
It can be seen that when worker produces complete set of parts severally,the total production number is 62;after considering which parts they produced more per unit time,the production plan was adjusted,and the total number of production sets was 94,which increased by half,resulting in a 50%increase in efficiency.Then,is 94 sets the maximum production?
Let's consider that worker A produces parts A and B are 80 and 40 respectively,and the efficiency ratio of producing two parts per unit time is 80:40=2:1;similarly,the efficiency ratio of worker b is 30:90=1:3;the efficiency ratio of worker C is 15:60=1:4.This shows that A has the highest efficiency in producing part A and C has the highest efficiency in producing part B.
III.Whoever Makes Which Part is the Most Efficient Will Be Arranged to Make the Part
We adjust the production plan,so that worker A only produces part A and worker c only produces part b.In order to form complete set,worker B makes both part A and part B.Set the time of worker B used to produce part A asx,then the time of producing part B is11xx,in order to match the A and B,we can get:
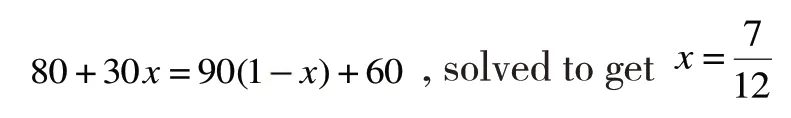
That is,the quantity that arrange worker B to produce part A issets,the quantity that arrange worker B to produce part B issets.The total number of parts is listed below:

Therefore,the total number of sets of parts produced is 80+18=38+60=98sets,4 more than the previous scheme.
It can be seen that,in the production process,the results may vary greatly with different production arrangements.In the 1960s and 1970s of the last century,we also seem to be able to appreciate Mr.Hua luogeng's efforts to promote the role of the unified planning method and the excellent selection method under the circumstances,and made outstanding contributions to the national economic construction.
Problems of increasing efficiency through scheduling can sometimes be solved by computers.For example,the following problems in linear programming:
A food factory uses rice as the main raw material to process A and B food,after 12 hours' processing,a bag of rice can get 3kg of A,with the profit of 24 yuan per kg.4 kg of B can also be obtained after 8 hours of processing,and each kg of B can earn 16 yuan.At present,the daily supply of rice raw materials is 50 bags,and the controlled quantity of labor hours is 480 hours,and due to the control of market demand,the maximum amount of processing is 100 kg of A.
How should the factory arrange production so as to maximize the profit after sales? What is the maximum?
We analyze the constraints,decision variables and objective functions of the linear programming problem,letx1bag of rice produce A,x2bag of rice produce B,and get the mathematical expression of the problem:
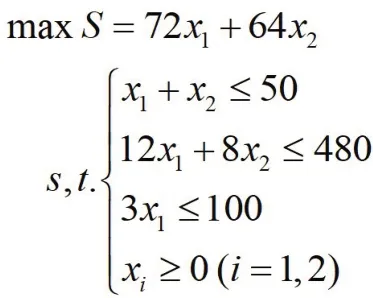
Because it's a linear programming problem with two variables,using graphical method then we can get:x1=20,x2=30.The maximum profit value is:(yuan).
However,if analyze the following problems:(1)Raw material supply is controlled.If you can buy a bag of rice for 35 yuan now,do you want to buy it?(2)Processing hours are controlled,if workers can be temporarily hired,what is the maximum hourly wage? (3)If the profit of product A increases to 30 yuan/kg,does the original production plan need to be adjusted? Even using graphical method these problems won’t be solved.It is a time of information age,the application of computer software is very wide,LINGO is a mathematical software to solve planning problems,the interface is simple,intuitive,and easy to understand,we can use it to solve the problem.
As shown in figure 1,input in LINGO interface:
After checking that there is nothing wrong with the program,clickon the menu,the following results are obtained:
It can be seen from the operation results in figure 2x1=20,x2=30,the maximum profit value is(yuan).The result is consistent with the graphic method.

Figure 1
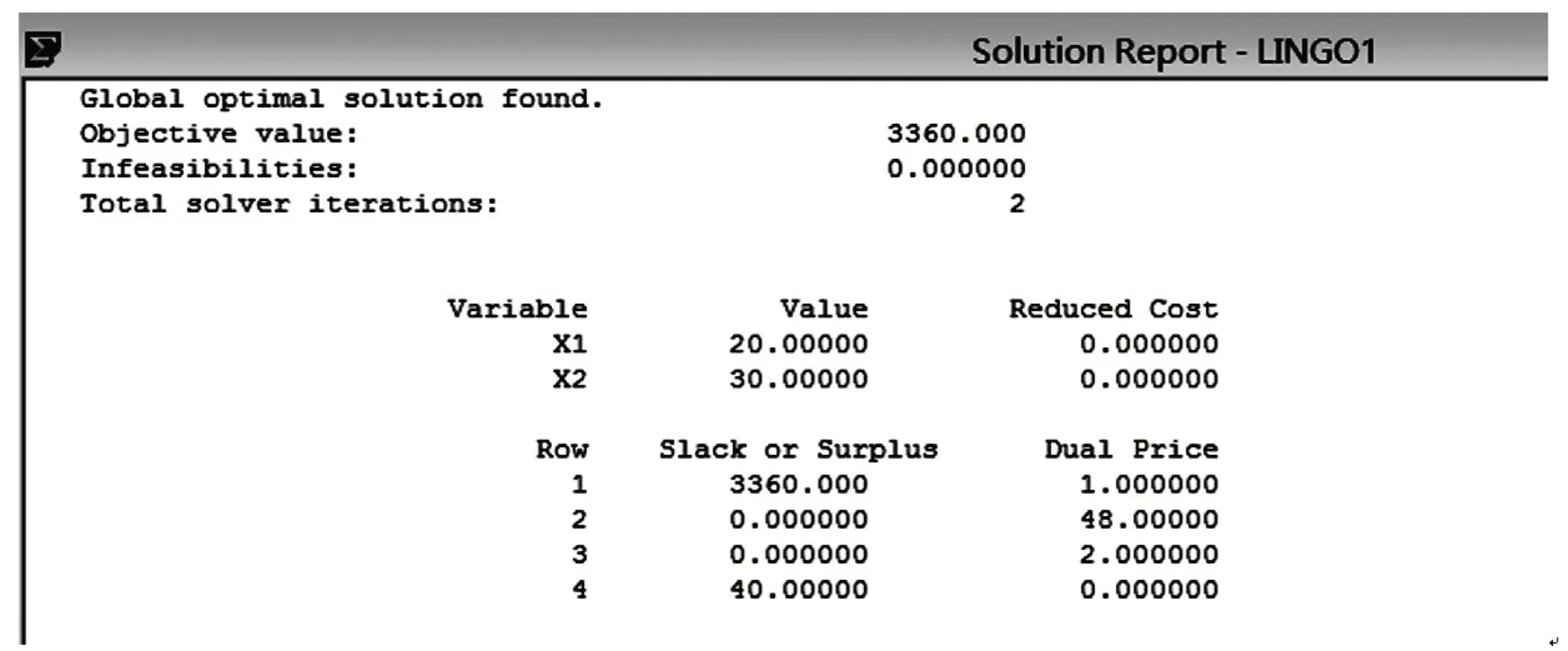
Figure 2
In addition,according to the shadow price in the above results,the surplus amount of raw rice is 0,and every additional bag of rice will increase the profit by 48 yuan.Since the cost of a bag of rice is 35 yuan,less than the 48 yuan increase in profit,it can be bought.The remaining amount of working hours is 0,and the profit will be increased by 2 yuan for each additional unit of working hours.Therefore,if the working hours are increased,the wages of temporary workers should not be more than 2 yuan/hour.The processing capacity of A is 40,and the increase of the processing capacity will not affect the profit,so the production plan will not be changed when A's profit increases to 30 yuan/kg.
You can't do it graphically if you increase the variables in the previous example,but LINGO still works,and graphical methods cannot analyze information such as shadow prices,which are important in the economy,for reference in economic decisions.However,with LINGO,it can be extended to the nonlinear programming problem,which can achieve many things at one stroke.
