计算机lingo软件在生产效率中的应用
2019-12-26熊莉
熊 莉
(湖北交通职业技术学院,湖北 武汉 430079)
笔者在课余时间读到了一些关于数学家华罗庚先生的生平及事迹的书籍,华罗庚先生是近代中国首位将数学理论研究应用于生产实践,并推动经济数学发展的数学家,他在晚年大力推广统筹法和优选法。
在平时生产中,安排生产的方式不同,效率会有很大区别,下面举一个例子来说明。
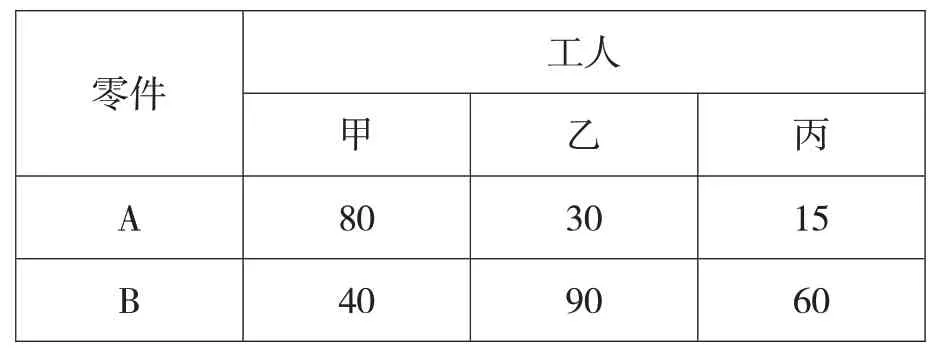
设某工厂安排三个工人生产两种不同的零件,在单位时间内工人甲可生产80个零件A或40个零件B,工人乙可生产30 个零件A 或90 个零件B,工人丙可生产15个零件A或60个零件B,每种零件各一个配成一套。那么,工厂应该怎么安排生产?
为了便于理解,我们将以上条件中的关键数据列表如下:
一、首先,假设工人各自为阵,每人自己生产可以配套的A,B两种零件
假设单位时间为1,工人甲用于生产零件A 的时间为x,用于生产零件B 的时间为1-x,则:80x=40(1-x),解得x=。此时,生产零件A,B 各件,构成27套。
同理,单位时间为1,工人乙用于生产零件A的时间为y,用于生产零件B 的时间为1-y,则:30y=90(1-y),解得y=。此时,生产零件A,B 各件,构成23套。
对于工人丙,用于生产零件A的时间为z,用于生产零件B 的时间为1-z,则:15z=60(1-z),解得z=。此时,生产零件A,B 各件,构成12套。
数据列表如下:

所以,生产零件的总套数为27+23+12=62套。
这种方式显然并没有发挥每个工人的特长,甲、乙、丙三人生产零件A,B 的快慢是不一样的。在单位时间内,甲生产零件A 数量最多,乙生产零件B最多,如果安排生产零件数量最多的工人只生产该零件又有如下方式。
二、谁生产哪种零件多就安排谁生产哪种零件
工人甲在单位时间内生产零件A数量最大,安排工人甲生产零件A;工人乙单位时间内生产零件B的数量最大,安排工人乙生产零件B;为了零件A,B 配套,工人丙就需要生产两种零件。设丙用于生产零件A的时间为x,则他生产零件B的时间为1-x,有:
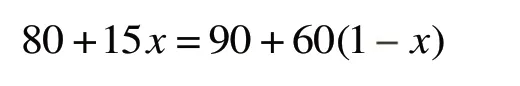
解得x=,丙生产零件A 的数量为件,生产零件B的数量为件。总的零件数列表如下:
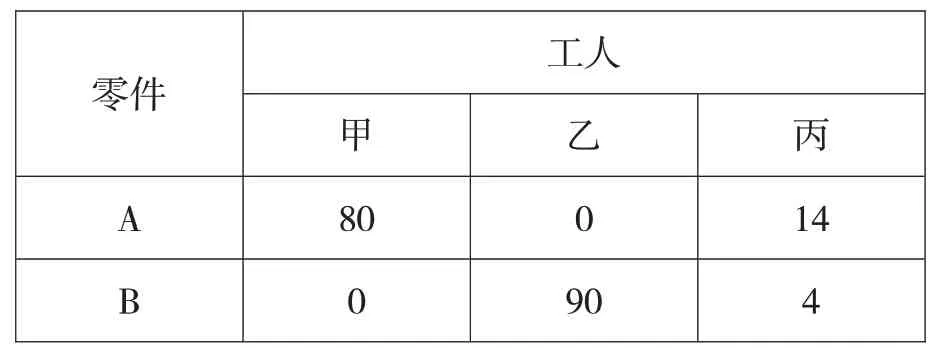
所以,生产零件的总套数为80+14=90+4=94套。
可见,工人各自生产成套零件时,总的生产套数为62 套;考虑他们单位时间内生产哪种零件多时,生产方案做了调整后,总的生产套数为94套,生产套数多了一半,使得效率提高了50%。那么,是不是94套就是生产的最大值呢?
我们再来考虑,工人甲生产A,B 两种零件的数值分别为80,40,在单位时间内生产两种零件的效率比为80∶40=2∶1;同理,工人乙的效率比为30∶90=1∶3;工人丙的效率比为15∶60=1∶4。这说明甲生产零件A的效率最大,丙生产零件B的效率最大。
三、谁做哪种零件的效率最大就安排谁做该零件
我们调整一下生产方案,让甲只生产零件A,丙只生产零件B,为了配套,乙既做零件A 也做零件B。设乙做零件A的时间为x,则他做零件B的时间为xx,零件A,B要配成套,有:
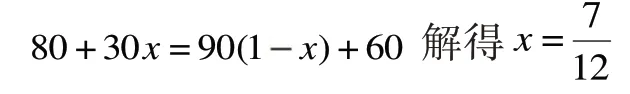
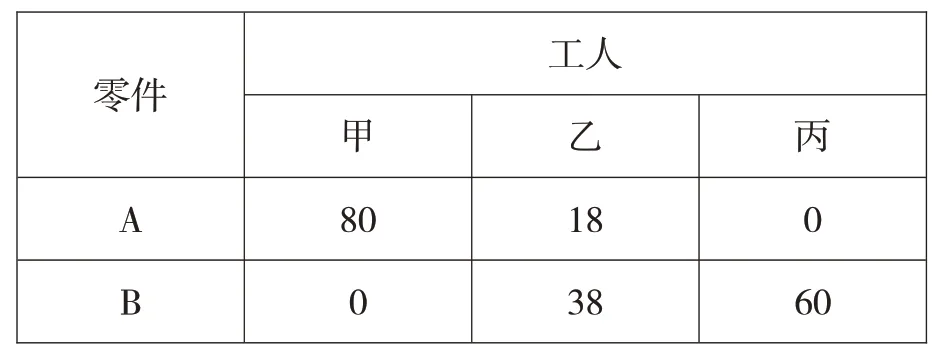
所以,生产零件的总套数为80+18=38+60=98套,比上一种方案又多了4套。
可见,在生产过程中,安排生产的方案不同得到的结果可能有很大差别。在上世纪的六七十年代,我们也似乎能够体会到华罗庚先生在当时的情况下极力推广统筹法和优选法的作用,为国民经济建设服务而作出的卓越贡献了。
通过生产安排以提高效率的问题有时候也可以借助计算机来实现。例如在线性规划中的下列问题:
某食品工厂用大米作为主要原料加工A,B两种食品,一袋大米经过12小时加工可获得3公斤A,每公斤A 可获利24 元;也可以经过8 小时加工获得4公斤B,每公斤B可获利16元,现在每天的大米原料供应量是50 袋,劳动工时的控制量是480 小时,而且由于市场需求的控制,最多加工100公斤A。
工厂应该怎么安排生产才能使得销售后获得的利润最大呢?最大值为多少?
我们分析该线性规划问题的约束条件、决策变量和目标函数,设安排x1袋大米生产A,x2袋大米生产B,得到该问题的数学表述:
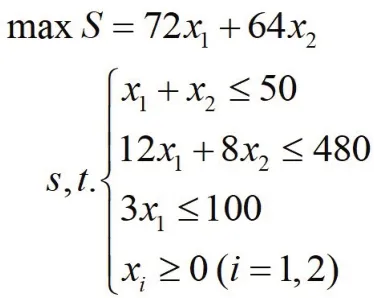
因为是两个变量的线性规划问题,用图解法可得:x1=20,x2=30。
但是,如果要分析以下问题:(1)原料供应有控制,如果现在35 元可以购买一袋大米,买吗?(2)加工工时有控制,如果工人可以临时雇佣,付出工资最多每小时几元?(3)如果产品A 的获利增加到30元/公斤,原来的生产计划是否需要调整?运用图解法中都不能解决。现在是一个信息时代,计算机软件的应用很广泛,LINGO是一款解决规划问题的数学软件,界面简洁、直观、易懂,我们可以借助它来解决问题。
如图1,在LINGO界面输入:
从图2 运行结果可知x1=20,x2=30,最大利润值为:(元)。与图解法结果一致。
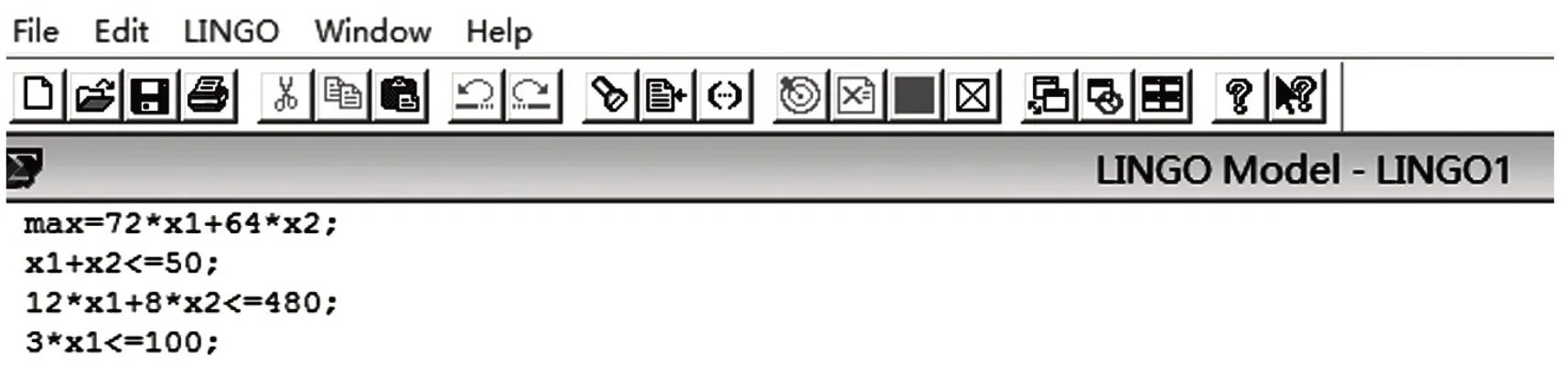
图1
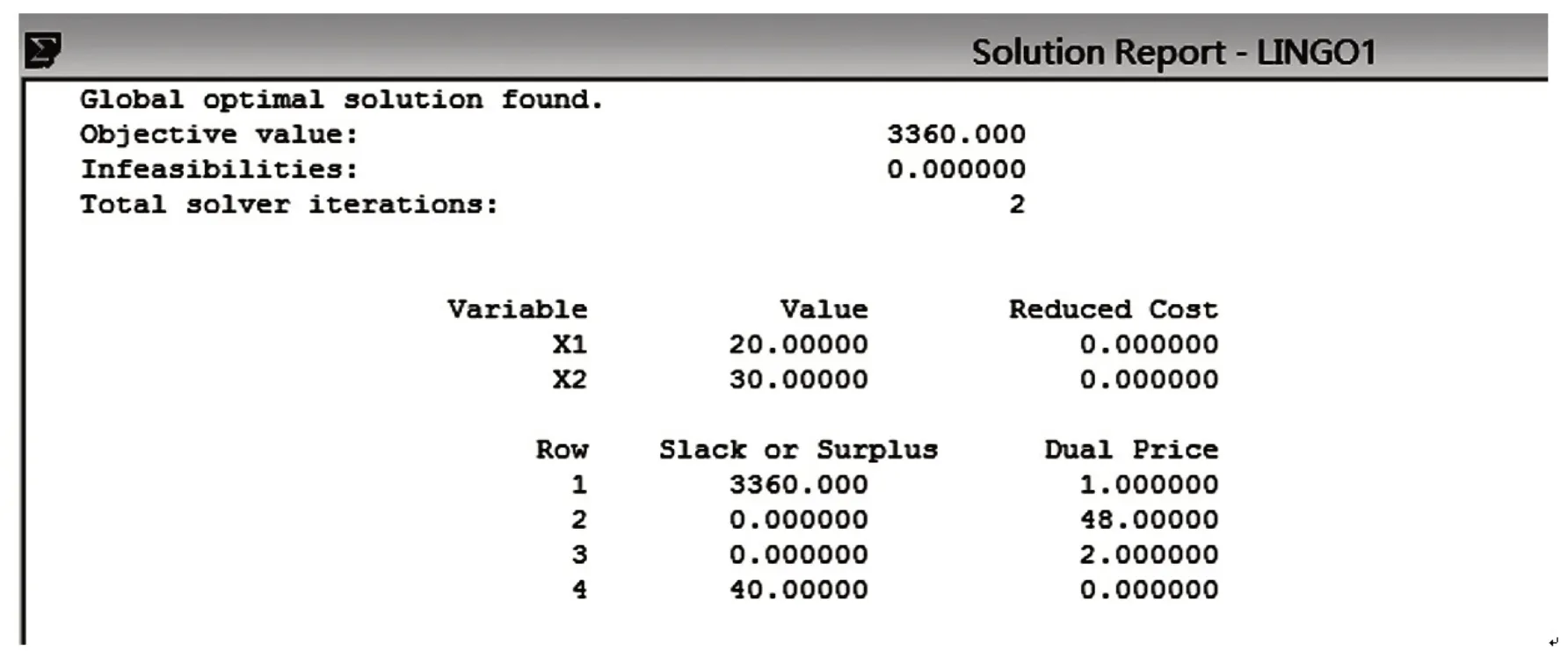
图2
此外,由上面结果中的影子价格可知,原料大米的剩余量为0,每增加一袋大米,利润增加48元,由于一袋大米的成本35元,小于它带来的利润增加量48元。所以可以买。工时的剩余量为0,每增加一个单位的工时,利润增加2 元,因此如果增加工时,临时聘用工人的工资应该不多于2元/小时;对A的加工能力剩余40,而且加工能力的增加不会影响利润,因此A 获利增加到30 元/千克时不会改变生产计划。
如果上例中变量增加的话就不能用图解法来做了,但是LINGO 求解仍然可行,并且图解法不能分析在经济中重要的影子价格之类的信息以此为经济决策做参考。而用LINGO求解,可以扩充到非线性的规划问题,可谓一举多得。
