基于遗传蚁群动态融合的地面自主作战机器人路径规划

李郁峰，李魁武，潘玉田，郭保全，余红英

(1.中北大学 电气与控制工程学院，山西 太原 030051；2.西北机电工程研究所，陕西 咸阳 712099)

在机器人路径规划算法中，遗传算法全局搜索能力强，但是反馈信息没被利用，增加了无用迭代次数，求解的效率变低[1-3]。而在蚁群算法中，信息素得到了不断积累与更新，从而收敛于最优路径。但由于初始阶段缺乏信息素，导致初期信息素的积累时间较长，收敛速度慢，且求得的解往往不是最优解[4-6]。

文献[7-8]针对两种算法的不足，提出了遗传与蚁群基本融合算法(Genetic Algorithm-Ant Algorithm,GAAA)。但是该基本融合算法的时间效率和求解效率都是在不同阶段使用不同算法，而不是真正意义上的融合，而且在后期蚁群算法中，由于收敛速度过快易陷入局部最优。

笔者在GAAA基本融合基础上，提出了一种动态遗传与蚁群融合算法(Dynamic Genetic Algorithm Ant Algorithm，DGAAA),包括遗传算法生成初始路径信息素与蚁群动态融合遗传算法两个阶段。

1 遗传算法生成初始路径信息素阶段

1.1 确定适应度函数

在全局与局部路径规划中，必须满足动态避障与路径最短的条件。采用栅格法建立环境模型。动态避障是比较关键的一个约束条件，已知障碍物的个数、位置和速度信息。假设自主作战机器人和各障碍物为匀速直线运动，因此可以不考虑机器人和障碍物运动速度的变化。动态避障的基本条件是：对于某一路径，组成路径的各点与各障碍物之间的最小距离必须大于机器人与障碍物的半径之和。

设机器人从当前点P0到Pi(xi,yi)需要的时间为ti，从P0至Pi-1(xi-1,yi-1)所用的时间为ti-1，从Pi-1(xi-1,yi-1)至Pi(xi,yi)所用的时间为Ti-1，则

ti=ti-1+Ti-1，

(1)

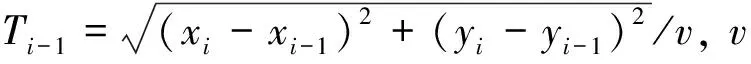
xbk(ti)=xbk(t0)+vkxti,

(2)

ybk(ti)=ybk(t0)+vkyti,

(3)

式中：(xbk(t0),ybk(t0))为第k个障碍物的起始坐标；vkx,vky为第k个障碍物的当前速度vk在xOy坐标系中的分量。

设在ti时刻，路径点Pi(xi,yi)与第k个障碍物的距离Dik为

(4)

则对于任意一条路径，路径上点与障碍物的最短距离Dmin为

(5)

式中:n是组成路径的点的个数;m为障碍物的个数。

由此可得动态避障的适度函数ffit1为

(6)

由式(6)可知，只要路径上各点与各障碍物的最小距离大于机器人半径R0与障碍物的安全半径Rk之和，则机器人就能完全避开障碍物，所以适应度为1，否则为0，这样确定是符合实际情况的。

选取路径最短个体适应度评价函数：

(7)

式中，D为相邻序号栅格之间的距离。

最后得到遗传算法的综合适应度函数为

F=ffit1·ffit2.

(8)

该综合适应度函数有机融合了两个约束条件，避免了两项加权求和所导致的优化不稳定问题。

1.2 自适应遗传算子

采用自适应交叉变异算子[9]，计算群体的平均适应度favg和最大适应度fmax，按照适应值大小将群体排序并分为两组。

1)交叉操作。首先判断种群的代数，若小于n，执行固定的交叉概率；若大于或等于n，执行自适应交叉概率。其中，n为固定操作的种群代数，自适应交叉概率Pc：

(9)

式中：fc为要交叉的两个个体中较大的适应度值；k1、k2为常数,k1≥0，k2≤1.

2)变异操作。首先判断种群的代数，若小于n，则执行固定的变异概率；若大于或等于n，则执行自适应变异概率Pm：

(10)

式中：fm为要变异个体的适应度值；k3、k4为常数，k3≥0,k4≤1.

2 蚁群动态融合遗传算法阶段

2.1 最佳融合点评估策略

基本融合算法中，两种算法的融合是通过设定固定的迭代次数来实现，致使种群进化效果不够理想。增加了无用迭代次数，使融合算法收敛速度变慢。因此，为了交叉地调用两种算法，提出一种最佳融合点评估控制策略[10-12]。过程如下：

1)蚁群算法生成初始种群，并更新全局最优解。

2)利用步骤1)中生成的最优解作为遗传种子并优化。

3)进入遗传操作，初期生成的所有种群借助于评估控制策略进行最佳融合点评估，根据条件判断是否进入蚁群操作。

评估控制策略步骤如下：

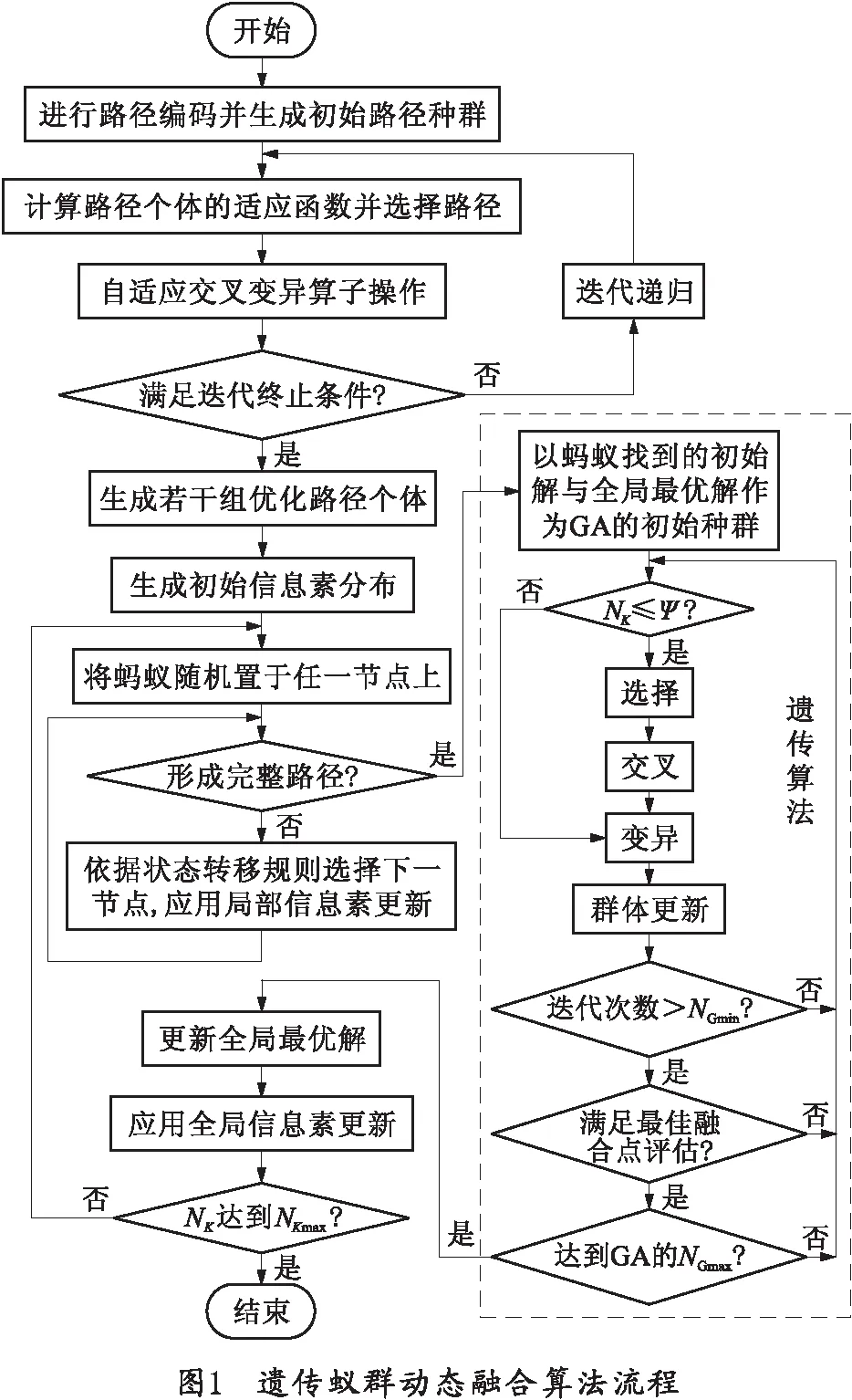
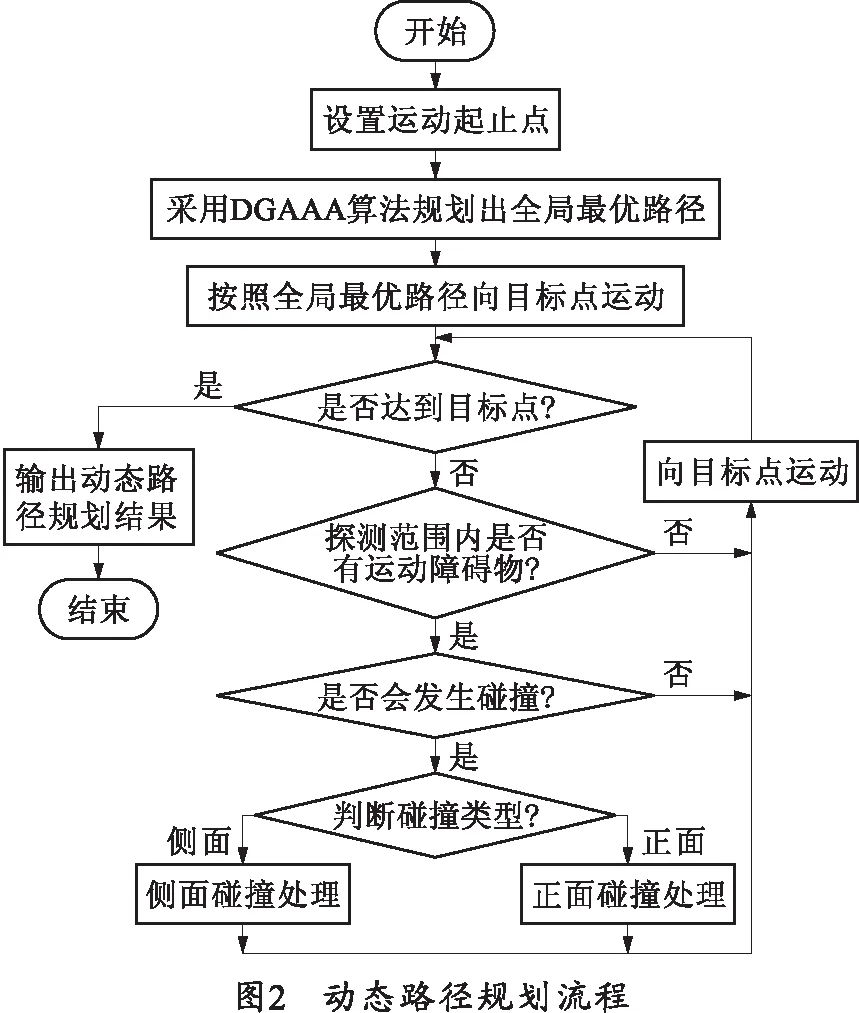
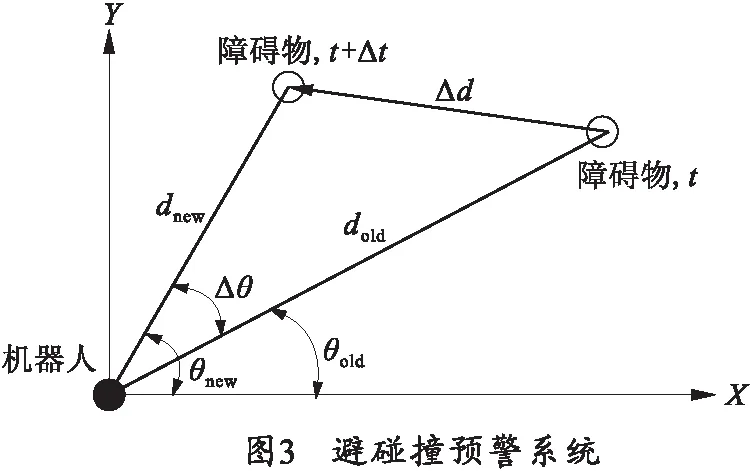
1)遗传操作中,为了确定迭代范围,设定最小迭代次数NGmin和最大迭代次数NGmax(NGmin

2)如果在迭代次数范围内，连续n代都满足

Δfn<Δfn-1，

(11)

采用式(11)动态交叉调用两种算法，控制它们的融合时机，以提高算法的自搜索能力、收敛速度。

2.2 信息素的更新

基本融合算法中，只通过蚁群算法的解和全局最优解更新信息素，使更新速度变慢，启发信息不能得到及时地更新。而动态融合算法则在基本融合的基础上，利用遗传算法中每一代种群最优的个体，再次更新信息素[12]。在最佳融合点评估策略的控制下，确保了种群进化方向。所以，该方法比基本融合方法能够更快、更好地反映各个路径的优劣，以便指导下一步的蚁群寻优并尽快找到最优解。

更新信息素的规则为

(12)

式中：Lgb分别为动态融合中现有种群中最优解、更新信息素时全局最优解的值;ρ为信息素的挥发系数，ρ⊂[0,1];τij为t时刻在(i,j)边上残留的信息激素量;Δτij(t)为经过时间Δt路径(i,j)上信息素的增量。

2.3 迭代调整阈值设计

在DGAAA算法中，为了避免算法运行后期遗传算法出现早熟，设计一个迭代调整阈值Ψ，对遗传操作和蚂蚁种群规模进行调整。

Ψ=ξNKmax，ξ∈(0.5,1),

(13)

式中，NKmax为DGAAA算法整体最大迭代次数。

若后期迭代次数超出了所设置的阈值Ψ，则只作变异操作。当变异结果优于当前染色体时才接受。通过蚁群算法可适当地增大群体的规模，以便进一步发现最优解。动态融合算法路径规划具体流程如图1所示。

3 实验分析

利用动态融合算法进行了静态全局与动态局部路径规划仿真实验。为了进一步验证算法的实用性，在地面作战机器人上进行了实地测试。

3.1 仿真实验

3.1.1 仿真参数的确定

遗传算法阶段中影响算法运行的参数众多，最为关键的是种群大小N、变异概率Pc、交叉概率Pm.设定遗传算法结束条件中最小迭代次数NGmin=20,最大迭代次数NGmax=100.N=30，Pc=0.8，Pm=0.09.DGAAA算法整体最大迭代次数NKmax=100，迭代调整阈值Ψ=75，m=60，Q=100，α=2，β=5，ρ=0.8.

3.1.2 局部动态环境路径规划仿真

局部动态路径规划流程如图2所示。

障碍物运动状态的位置信息是通过传感器实时计算得到。根据避碰撞预警机制[13-14]，已知作战机器人R的运动速度和方向，由前后两个采样时刻(t,t+Δt)获得的障碍物O相对机器人R的位置信息，计算出障碍物O的运动状态。如图3所示，机器人相对全局坐标系速度vv和方向θv已知，O在t和(t+Δt)时刻相对机器人的角度(θold，θnew)和位移(dold，dnew)可由传感器测出，可以计算获得O相对全局坐标系的运动速度vo和方向θo.

障碍物相对机器人的速度为

(14)

根据图3中的几何图形三角变换关系，可得到变换的中间变量

(15)

可以确定障碍物相对机器人的偏角如下：

如果dold

1)如果θold>θnew，则θo/v=θnew+γ2.

2)如果θold<θnew，则θo/v=θnew-γ2.

3)如果θold=θnew，则θo/v=θnew.

如果dold>dnew，障碍物是向靠近机器人的方向运动的，则：

1)如果θold>θnew，则θo/v=θold-π-γ1.

2)如果θold<θnew，则θo/v=θold-π+γ1.

3)如果θold=θnew，则θo/v=θold-π.

障碍物相对全局坐标系的运动速度和角速度为

(16)

(17)

(18)

当作战机器人可能与动态障碍物碰撞时，由当前障碍物的方向与速度，通过提前改变方向来避开动态障碍物。采用静态障碍物环境作为环境模型，动态障碍物从右往左运动，正面动态避障过程如图4所示。侧面动态避障过程中，动态障碍物从下向上运动如图5所示。

在该实验设定的动态环境下，利用基于DGAAA的动态局部路径规划，机器人能够成功避开动态障碍物，运行时间1.349 s，相比基本融合算法GAAA的运行时间1.441 s，DGAAA算法在实时性上得到较大提高。这表明该算法在动态的环境下也能完全成功地规划出近似最优的路径。

3.2 作战机器人路径规划实验

地面作战机器人可以应用于多种野外环境，具有很强的环境适应性。为了进一步验证笔者提出动态融合算法DGAAA的实用性，在校园内选取实际的障碍物环境分别用DGAAA与基本融合算法GAAA进行了测试。路径规划实验结果比较如表1所示，路径规划实验过程如图6所示。

表1 路径规划实验结果比较

地面作战机器人在得到通过视觉、超声及红外传感器返回的环境信息后，经过信息处理、数据融合，得到障碍物的深度信息。通过非结构化道路检测，获得可通行区域，并利用立体视觉匹配重建得到障碍物的形状、尺寸等信息，利用遗传蚁群动态融合算法进行路径规划。

从实验结果比较和路径规划过程分析，作战机器人基本完成了系统的要求。在进行大量的实验中，DGAAA能够规划一条从起始点到目标点的最优或次优路径。相比GAAA算法，DGAAA应对环境变化的反应时间更快，并在行进过程中避开障碍物的成功率更高。

4 结束语

在基本遗传和蚁群融合算法的基础上，提出两种路径算法动态融合策略用于地面作战机器人的路径规划中。通过动态融合，采用最佳融合点评估控制策略，设计了相应的信息素更新方法，引入迭代调整阈值较好地克服了停滞，并能达到更好的路径规划效果。实验结果表明，在复杂环境下，相比基本融合算法，该算法能够更好更快地实现全局静态和局部动态路径规划。