基于复变函数解法的桁材开孔腹板弹性屈曲分析

杨 源，莫中华，唐文勇，孙启荣，沈亚明

（1.南通中远海运川崎船舶工程有限公司，江苏南通226005；2.上海交通大学海洋工程国家重点实验室，上海200240）

0 引 言

在船体梁总纵弯矩作用下，甲板纵桁和船底纵桁承受较高的轴向压力，结构设计时要确保它们具有足够的屈曲强度。但是，出于人员、管路穿行和结构减重的目的，纵桁的腹板上不可避免地会布置一些开孔。开孔形状以腰圆形和圆形较为常见，孔尺寸相比板格短边长一般较大，此时开孔对板格屈曲强度的影响值得关注。由于开孔的存在，结构分析域的形状变得不规则，面内应力发生了重分配，依靠纯解析方法难以准确处理该问题。

早期，Schlack[1]采用Ritz法研究了中心开圆孔的矩形板格受压屈曲问题，在小孔径、方形板条件下的计算结果与试验结果大体接近，这种模型过于理想化，实用价值有限。近年来，El-Sawy[2]、褚洪[3]、李政杰[4]等采用有限元法研究了开孔板弹性屈曲压力的各种敏感性因素。潘祖兴[5]以复变应力函数重构法配合区域划分法研究了带矩形开孔的矩形板屈曲，结果准确性高，只是区域分解法更适于通过简单分解即可获得较规则子区域形状的开孔结构域，不易推广到其他开孔形状的情形。本文聚焦船体结构中常见的开腰圆孔矩形板格的板边受压弹性屈曲问题，以复变函数方法完成开孔板平面应力计算，以基于背景网格的Ritz法计算弹性屈曲载荷，形成了一种有别于有限元的半解析算法，可应用在船体结构设计校核中。

1 开孔板的平面应力计算

待分析问题的力学模型如图1所示，在矩形板的中部存在一个腰圆形的开孔，开孔板的外板边可能受到单向或两向的压应力作用，不考虑体力作用。开孔板的长、宽、厚分别标记为a、b、t，孔的长轴、短轴的长度分别标记为lx、ly，孔心位置以坐标( xh,yh)来表示，E、μ 为板材料的弹性模量和泊松比。计算开孔板格屈曲首先要确定板上任意一处位置的平面应力状态量( σx,σy,τxy)。

根据Muskhelishvili提出的复变函数解法[6]，体力为0 时，均匀各向同性材质下的弹性平面问题的应力状态解可由两个复解析函数φ( z )和ψ( z )决定。各向应力、面内位移与φ( z )、ψ( z )之间存在如下的关系：

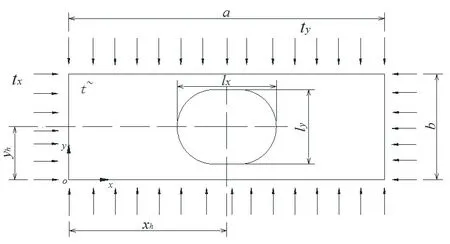
图1 分析模型示意图Fig.1 Diagram of analytical model

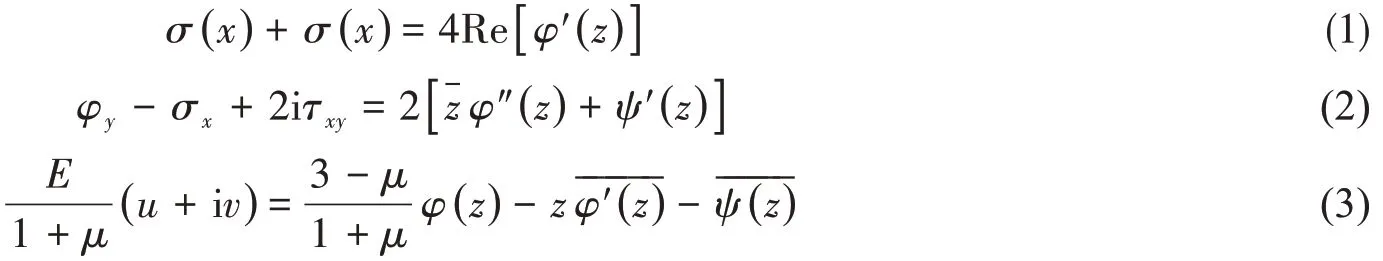
对于非圆形孔口的计算一般要进行保角变换处理，将弹性体在z平面上所占的区域变换为平面上以ξ = 0 为原点，1 为半径的单位圆内部区域，此时的保角变换关系可表示为z = f( ξ )。将其代入φ1( z)和ψ1( z )中，z的函数变为ξ的函数，函数的单值解析性质不变，有

根据复变函数理论，在环形区域内单值解析的函数可展开成Laurent 级数，且这种展开应是唯一的。故可设：

（10）-（11）式中，Ak和Ck为复常数，k= 0对应的常数项对分析无影响，可不考虑。为编程方便，上式进一步转化为函数g( ξ )的线性组合，未知量变为实常数αk和βk，共8n个。

采用最小二乘边界配点法[5-9]，构建边界条件的限制方程。边界面力tx，ty与应力σx,σy,τxy的关系如下：

式中，nx和ny为边界法矢的方向余弦。本模型包括内外两部分边界，内边界为腰圆形孔边，边界面力为0，外边界为矩形，边界面力为法向压力。将内、外边界等距离散为M个点，在每个点j上，用resj表示x,y两个方向上应力残差的平方和：

最接近精确解答的参数{ αk} ，{βk} 应使各点处的resj之和最小，故有

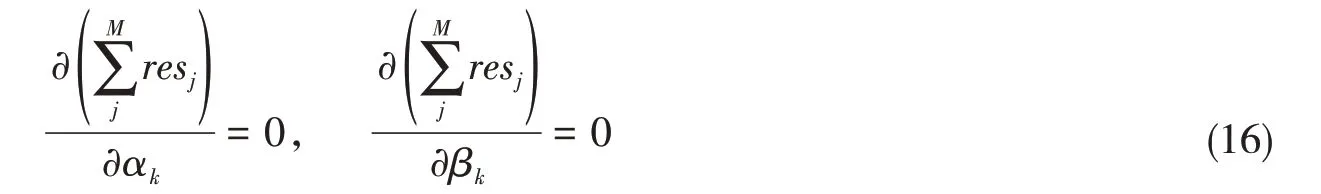
上式形成8n个线性方程，以求解未知参数{αk} ，{ βk} ，k为1至4n的整数，从而进一步确定结构域内每一点处的平面应力状态量。

2 开孔矩形板的弹性屈曲分析

假设在板边的面内压力作用下，开孔板正处于中性平衡状态。扰动引起结构发生偏离初始构形的微弯，结构域Ω内任一点( x,y )的挠度记为w，假设：

式中，Aj为未知常数，qj( x,y )为满足结构位移边界条件的基函数。基函数的选取与板的面外边界条件有关，本文主要关注四边简支情况，不妨继续采用经典矩形板的基函数构造形式：

此时，腰圆孔的出现增加了一道内圈的孔边界，模型的孔边是完全自由的，挠度未受限制，因此（18）式是满足位移边界条件的，但孔边弯矩和剪力均为0，这两项力边界条件则不再能够通过假设的基函数自动满足。因此为获得较准确的结果，需要增加N的数目，后面的算例说明22项的基函数组合已可获得足够准确的解。

开孔板的弯曲变形能Vε可表达为

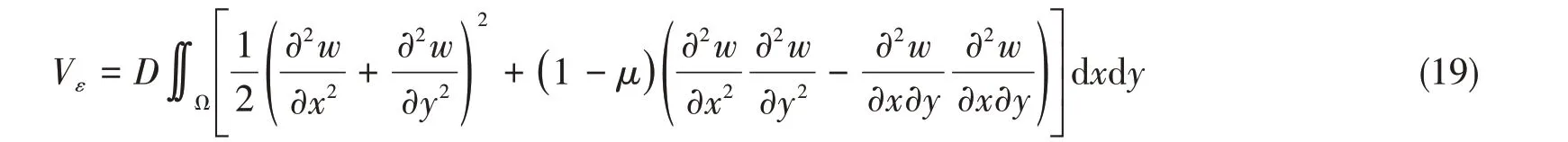
而在板边单位压力作用下外力功W为

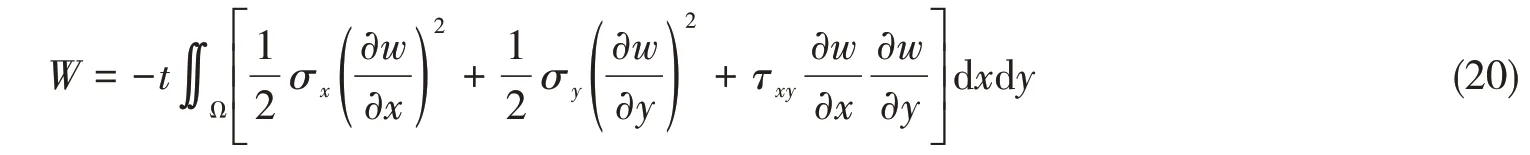
式中，D = Et3/[ 12( 1 - μ2)]，表示板的挠曲刚度。结构位能U = Vε- λW，λ代表施加的板边压力载荷。根据位能驻值原理，有

中性平衡状态下板结构挠度解的不唯一，表现为方程组系数矩阵的奇异，使屈曲临界载荷的计算转化为矩阵特征值的计算。对开腰圆孔的矩形板，板内各处的平面应力σx，σy和τxy不再是简单的均匀分布或线性分布关系，积分域Ω 的形状也是不规则的。显然，直接从整体的积分域出发来计算（22）-（23）式的积分比较困难，因此将结构域离散为三角形来实施积分计算。

这时结构域离散生成的网格属于背景网格，不影响板结构挠曲面的连续性。在离散得到的三角形积分域内可使用二维Gauss积分方法计算积分，矩阵MA，MB的元素可表示为

上式采用二维四点Gauss 积分公式[10]，ws为第s 个积分点的权重，Ar为离散得到的编号为r 的三角形面积，(,)为编号r 的三角形中第s 个积分点在总体坐标系下的坐标。每个积分点位置处的面内应力σx、σy，τxy由上一节所述的平面应力计算方法确定。

3 典型算例分析

参照图1 取一典型的船体桁材板格，ls= 0.8 m，ly= 0.6 m，a = 2.55 m，b = 0.85 m，t = 0.01 m，孔的中心与板的中心重合，矩形板的长板边不受面力，短边受1 MPa的均布压力。平面应力计算时，短板边等分为20段，长板边等分为60段，腰圆形孔边按1/4圆弧长等分20段的密度离散，然后取每一段的中点位置作为边界计算的配点，Laurent展开的参数n取30。计算在Matlab 7.7下编程实现。开孔腰圆孔的保角变换参照文献［11］的做法进行，获得的保角变换关系如（26）式，变换前后的内外边界线见图2。

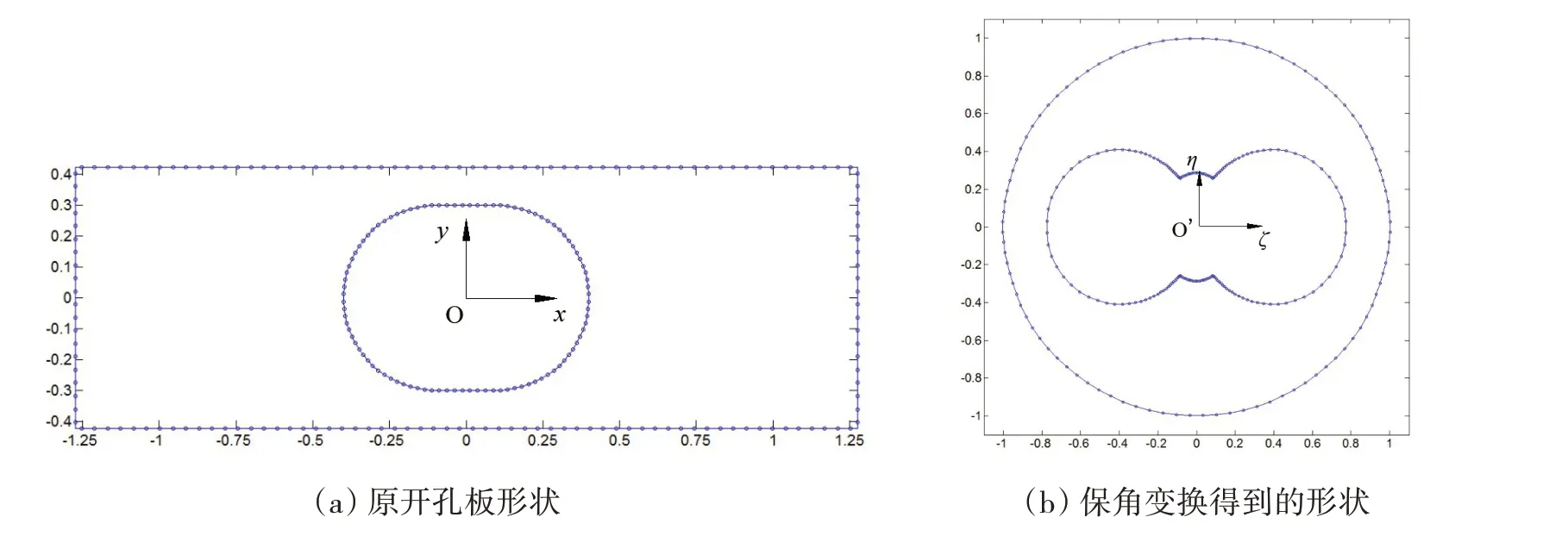
图2 保角变换示意图Fig.2 Diagram of conformal transformation

Matlab 编程计算开孔板的平面x 向应力如图3 所示。考虑到应力分布的对称性，在如图4 所示的1/4 对称腰圆孔边上，取弧长等分点处的孔边切向应力σθ结果，与ABAQUS 6.10 下的有限元平面应力解对比，显示于表1。作为对比基准用的开孔板格有限元模型，腰圆孔边网格尺度取0.012 m，外矩形板边网格尺度取0.025 m，在两者间的区域网格尺度逐渐过渡，以确保得到的孔边应力足够准确。表1中除了序号为7、8 的两个计算点由于应力结果的绝对值较小而反映出较大的相对误差外，其他11 个计算点的相对误差率均在4%以内。考虑到应力集中效应在孔边最大，开孔板上其他位置处应力的误差将更小，可见复变函数解法的开孔板格应力计算是比较准确的。

图3 短边受压下的开孔板σy应力云图 Fig.3 σy stress contour of perforated plate under longitudinal axial compression

图4 孔边应力σθ计算点示意图Fig.4 Diagram of calculation points for tangential stress σθ around the oval hole

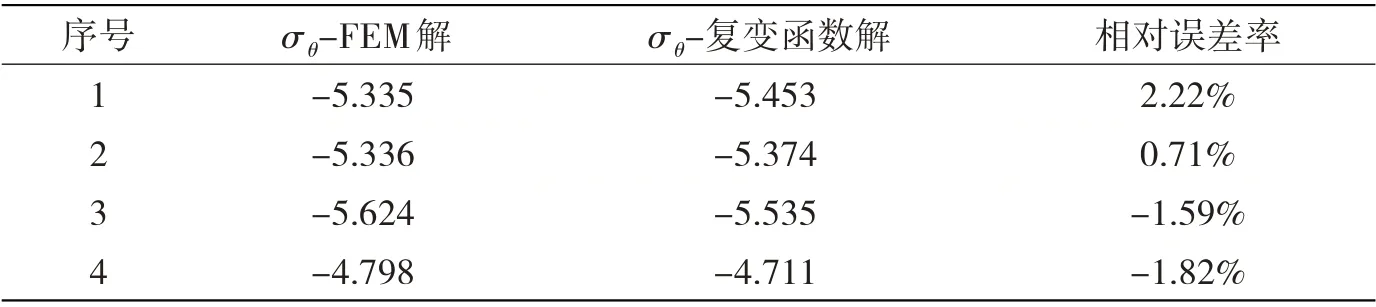
表1 孔边应力σθ计算对比Tab.1 Comparison of tangential stress σθ around the oval hole

续表1

屈曲载荷计算环节的域网格离散采用较粗的三角形网格，基于Delauney 三角化方法实现，如图5所示。计算采用（24）式的构造形式，以22 项基函数的线性组合来近似板的挠曲面，具体参数见表2。

有限元特征值屈曲作为对比方法，在ABAQUS 6.10 下建立2 种网格的有限元模型。第一种如图6 所示，为global mesh size=0.05 m 下以Free 方式划分得到的有限元网格模型，以四边形单元（S4R）为主，辅以三角形单元（S3），记作有限元模型I。这种网格较密且均匀，经过验证更密的网格对计算结果影响已经比较微弱，可认为这种网格密度下的分析结果准确度是足够的，以此作为对比的基准模型。第二种采用如图4 所示的三角形背景网格，生成三角形单元（S3）离散的有限元模型，记作有限元模型II。两种有限元模型在加载时均采用shell edge load 方式施加板边的面内压力，并在矩形的3 个顶点处施加适当的面内约束，限制模型的刚体位移，特征值屈曲计算选用兰索斯迭代算法完成。

图5 算例采用的积分背景网格Fig.5 Integration background mesh of the example

图6 对比用的有限元模型Fig.6 Finite element model for comparison

表2 算例采用的基函数序列Tab.2 Basis functionse quence of the example

表3 算例的对比结果Tab.3 Comparison of results for the examples

计算结果如表3 所示，本文方法的屈曲临界压力解与有限元模型I 解比较接近，存在-0.56%的误差。本文方法得到的1 阶屈曲变形模态如图7 所示，亦与有限元模型I的基本一致。负偏差则可能来自域离散的数值积分，这一点通过加密背景网格的验算可初步验证。若将M2背景网格的密度分别增加为原来的2 倍和3 倍，相应的弹性屈曲解分别为116.92 MPa 和116.89 MPa，与有限元模型I 的解已非常接近。而有限元模型II 的解则出现了7%以上的明显结果偏差，这反映出背景网格和有限元网格存在着明显差别。

图7 本文方法获得的一阶屈曲模态变形Fig.7 First-order buckling mode deformation obtained by this method

有限元方法采用分片位移场假设，网格离散对位移场连续性的削弱在网格较稀疏时会引起明显的误差，需要通过足够密的网格来保证精度。而本文方法在平面应力和屈曲载荷计算中均采用了完全连续的位移场假设，网格的离散只是为了不规则形状域下的数值积分计算，故本文方法对于网格离散的依赖度较低。

4 敏感性对比验证

在展示开孔板格弹性屈曲载荷敏感性的同时，本章进一步展示本文方法的准确性。敏感性对比计算中，均采用与上一节相似的网格离散。

首先，通过设定不同的x、y 向板边压应力比，可获得如图8 所示的弹性屈曲结果曲线。以ABAQUS 解为基准，本文方法的结果误差率在2%以内。误差率随着长边受压比重的增加有微弱增加。板格在短边受压为主时，可获得较高的屈曲承载能力，故这种情况在船体结构校核上也更常见，下面的计算主要针对短边受压情形展开对比。

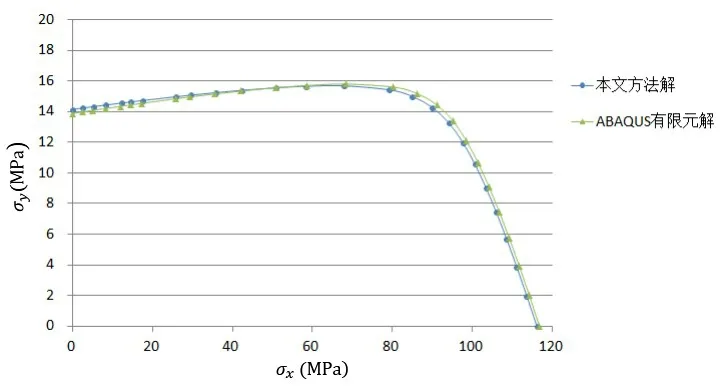
图8 双向轴压作用的弹性屈曲解Fig.8 Elastic buckling solution under bi-axial compression

将腰圆孔沿x轴方向朝左侧逐渐移动，分别计算xh从1.275 m逐步减小至0.575 m的弹性屈曲压力解，结果如表4。当xh大于0.675 m时，本文方法与ABAQUS有限元解的吻合度较好，以ABAQUS解为基准，本文方法的结果误差率保持在1%以内。当开孔距离孔边较近时，本方法的误差开始增大，这与有限的基函数选取不能反映过于局部化的挠曲变形有关。

表5～7分别反映了腰圆孔形状、矩形板长度a和宽度b的变化对屈曲临界载荷的影响，以ABAQUS解为基准，本文方法的结果误差率均在1%以内。可以看出，以腰圆孔倍率表示腰圆孔长轴长度与短轴长度之比，腰圆孔倍率越高，弹性屈曲解也越大；弹性屈曲解随矩形板长度a的增大而逐渐减小，但a>2.85 m后，弹性屈曲解的减小幅度已十分微弱；弹性屈曲解随矩形板宽度b的增大而逐渐减小。

表4 腰圆孔位置的敏感性效应Tab.4 Sensitivity to oval cut-out location

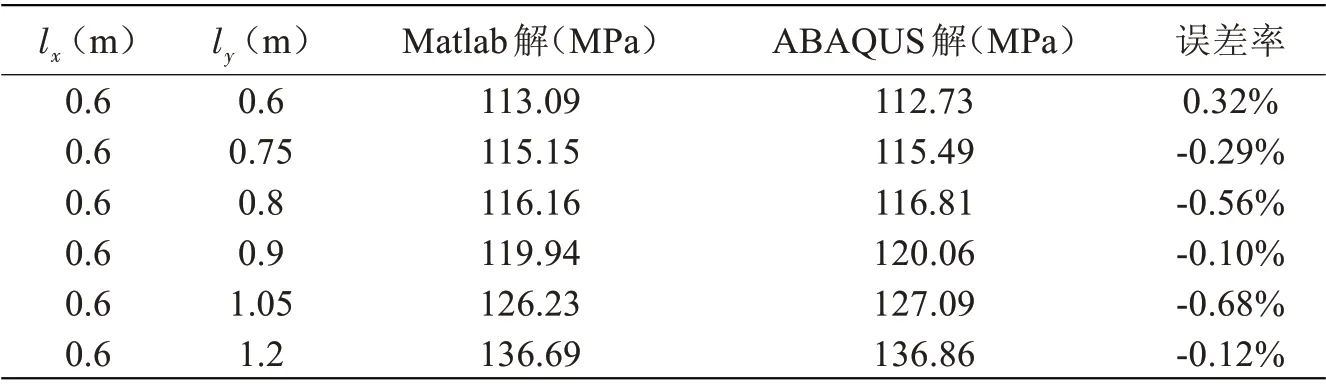
表5 腰圆孔倍率的敏感性效应Tab.5 Sensitivity to oval cut-out shape

表6 矩形板长边长度a的敏感性效应Tab.6 Sensitivity to rectangular plate long-side length

表7 矩形板短边长度b的敏感性效应Tab.7 Sensitivity to rectangular plate short-side length

5 结 语

对船体桁材开孔腹板的屈曲问题，本文提出以改进的复变函数方法计算板内的平面应力，结合背景网格积分下的Ritz 法，确定开孔板格的弹性屈曲载荷。该方法基于完全连续的面内和面外位移场假设，对网格的依赖性相比有限元已有明显的削弱，可以在较粗的域离散网格下获得十分准确的弹性屈曲解。通过与ABAQUS 屈曲有限元结果的系列对比，本方法能够较好地反映双向受压、孔位移动、腰圆孔倍率、矩形板长度和宽度变化的敏感性影响，具有良好的结果精度，可用于设计阶段船体桁材开孔板格的屈曲校核。