考虑实测初挠度、厚度和残余应力等缺陷的耐压球壳极限承载力分析

2019-12-25王永军蔡新钢黄进浩潘广善

船舶力学 2019年11期

张震，王永军，蔡新钢，黄进浩，潘广善，秦天

（中国船舶科学研究中心，江苏无锡214082）

0 引言

“十三五”期间，我国提出了深海进入、深海探测以及深海开发的海洋发展战略。深海装备的开发是实施这一战略的重要保障。与陆地环境不同的是，在深海作业的设备必须能够承载较大的水压，以确保其不被破坏。因此，耐压结构是深海设备的关键部件，它直接决定了设备整体的安全性和可靠性。

由于其优良的承压性能，球壳常被用作深海设备的耐压结构，如潜艇球面舱壁、潜器载人舱以及深海设备耐压壳等。耐压球壳极限承载力计算是球壳结构设计过程中的重要环节，其计算结果的准确性直接决定了深海设备安全储备大小，较大的计算误差势必导致耐压壳体重量的增加，从而影响深海设备整体性能的发挥。

结构极限承载力即结构所能承载的最大载荷，超过该载荷值后，结构发生破坏，破坏的基本型式包括：较大的局部塑形变形、屈曲和断裂。一些结构的破坏也经常包含以上三种型式的组合。例如，局部塑形变形会伴随屈曲发生，局部屈服会降低结构的稳定性。当前深海耐压壳体多数采用高强钢或钛合金制造，壳体壁厚较小；另一方面，根据耐压壳体的力学特性，其载荷几乎全部由薄膜压缩来承受。以上因素导致其破坏形式多为屈曲。屈曲主要有线性和非线性屈曲。由于制造工艺的影响，几乎所有的球壳均含有一定的缺陷，从而导致多数球壳结构为非线性屈曲。多年来，各国学者针对球壳的非线性屈曲问题进行了大量的理论和试验研究。美国和俄罗斯科研人员通过大量试验得出了关于球壳极限承载力的经验公式。近年来，我国学者围绕大深度潜水器耐压球壳的设计进行了不懈的探索。刘涛[1]通过引入非弹性段的材料弹性模量，给出了较厚球壳的屈曲压力简易计算公式；王自力等[2]研究了初始几何缺陷对球壳极限承载力的影响规律；潘彬彬等人[3]研究了各国船级社关于球壳极限强度的设计公式，指出其公式过于保守，需要制定统一的球壳设计公式，并结合有限元方法推导出适用于钛合金球壳的经验公式。

由前述研究可以看出，解析法和非线性屈曲分析有限元法是当前耐压球壳极限承载力计算的主要方法，由于其针对影响极限承载力的因素处理方式不同，计算结果有时会相差很大。本文在非线性屈曲分析有限元法的基础上，以实测初挠度替代计算过程中所采用的线性屈曲模态，并增加实测厚度和残余应力的成分，采用ANSYS 软件的APDL 语言编制了计算程序，使得计算模型更加接近真实情况。为了验证该方法的有效性，加工了直径1 000 mm 的球壳，分别进行了加工成型后的初挠度测量、厚度测量、残余应力测量以及水压试验。

1 计算方法

1.1 解析法

Zoelly 于1915 年采用小挠度理论推导出了理想球壳结构的极限承载力计算经典公式，该公式假设材料均匀且各向同性，材料应力应变符合线性关系，结构无初始缺陷。

许多试验结果表明，耐压球壳的极限承载力远低于公式（1）所给出的计算值，这是由于经典理论所做的假定过于严格，几乎所有耐压球壳均不能满足上述全部假定条件。

随后，美国泰勒水池经过大量试验得到了考虑制造工艺因素的极限承载力计算公式[4]：

式中，Es和Et分别是材料的割线模量和切线模量，cz是制造影响系数，tcr是临界弧长上的壳板平均厚度，Rcr是球壳外表面的局部曲率半径。

俄罗斯Krylov 研究院Paliy 等对耐压球壳的极限强度进行了理论和试验研究，提出耐压球壳的临界压力公式[5]：

式中，f 为耐压球壳最大初挠度，t 为球壳厚度，f'为初挠度系数，σe为经典理论（公式（1））所得到的球壳应力，σs为材料的屈服极限，β为综合考虑了材料性能、几何缺陷等因素得到的制造效应系数。

潘彬彬等人[6]采用有限单元法针对不同尺度和缺陷的钛合金球壳结构进行了数值模拟，得到了用于钛合金球壳极限强度评估的经验公式，并通过四只钛合金球壳模型验证了该经验公式的准确性。目前，这一经验公式已被吸收进CCS规范，应用于潜深大于500 m的钛合金外压球壳极限强度计算：

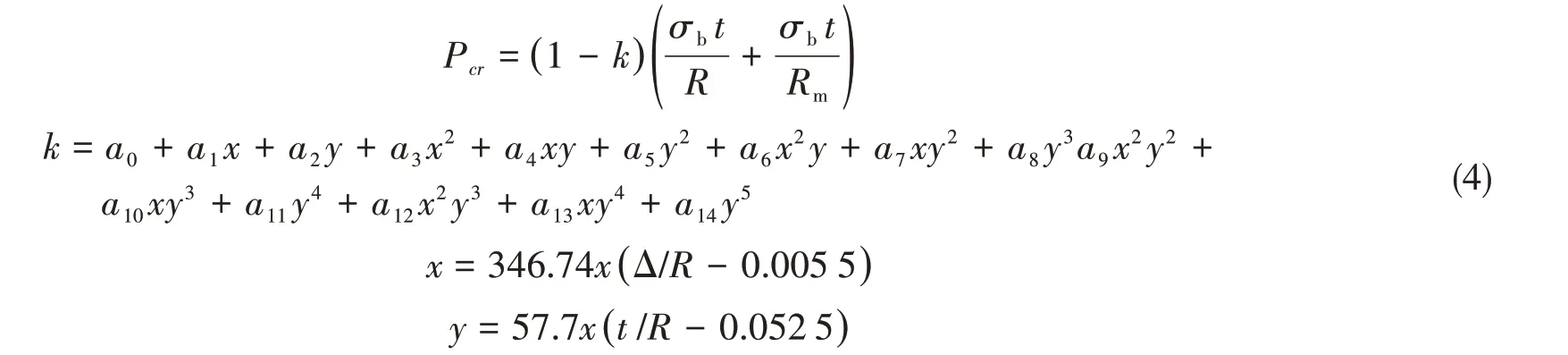
式中，k为制造修正偏差系数，t为球壳厚度，Δ为球壳制造最大允许偏差，R为球壳内半径，Rm为球壳中面半径，σb为材料抗拉强度。

泰勒水池公式和俄罗斯公式通过一衰减系数的方式考虑了初始缺陷对耐压球壳承载力的影响，但计算结果偏于保守[7-9]。另外，俄罗斯公式作为球壳的稳定性校核公式，其应用前提是球壳的应力小于规定的许用应力，具有一定的局限性。潘彬彬等人的公式是根据钛合金材料性能推导得出，对于钢制结构尚未有大量的试验验证。

1.2 非线性屈曲分析

伴随着计算机科学和技术的快速发展，数值分析方法得以大规模应用。特别是经过近30年的发展，有限单元法的基础理论和方法已经比较成熟，成为工程领域应用最为广泛，成效最为显著的数值分析方法[10]之一。

基于有限单元法的耐压壳体极限承载力计算主要包括特征值屈曲分析和非线性屈曲分析。特征值屈曲分析对应于分叉屈曲破坏型式，主要针对完善型球壳结构，计算结果远大于试验值。目前，应用较为广泛的是基于初挠度的非线性屈曲分析方法，计算流程见图1。首先进行特征值屈曲分析，得到某一阶屈曲模态。然后将屈曲模态值乘以初挠度系数，施加于非线性屈曲分析有限元模型，用于模拟耐压球壳初始几何形状，输入材料非线性参数后，即可进行求解，得到非线性屈曲临界载荷。

图1 非线性屈曲分析流程图Fig.1 The flow chart of nonlinear buckling analysis

相比于解析法，数值方法能够更加准确地求解相应的物理方程，降低计算误差。但基于特征值屈曲模态的非线性分析方法仍具有一定的缺陷。首先，非线性屈曲分析方法以特征值屈曲形状作为初始缺陷施加的依据，显然与实际形状有出入，导致其计算结果偏于保守[8]。另一方面，计算过程中并未涉及球壳制造过程中的残余应力和壳板厚度偏差等因素。因此，有必要开展基于实测数据的耐压球壳极限承载力的计算研究。

2 试验模型

2.1 试验模型介绍

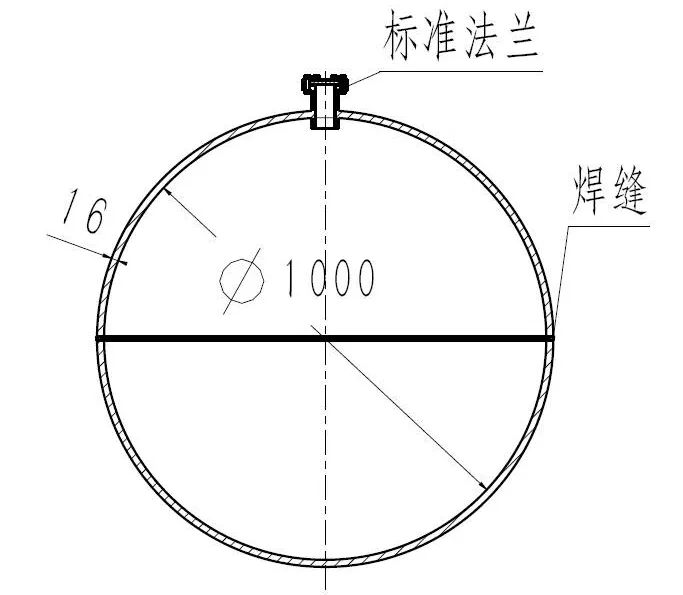
图2 试验模型结构图Fig.2 Drawing of test model

试验模型内径为1 000 mm，名义厚度16 mm，材料为Q345R，材料性能见表1，详细尺寸见图2。试验模型由两个同一批次同一规格的整板冲压半球焊接而成，模型上端设有注水孔，水压试验时便于向球壳内部注水，以减缓球壳破坏对试验设备的冲击。

试验模型的制造工艺流程见图3：熔炼得到的钢锭通过轧制得到一定厚度的钢板，并经过性能热处理后，整板冲压成半球；然后对冲压成型后的半球进行消应力热处理，并组焊，焊接方式为手工焊条电弧焊。探伤成功后，试验模型即制造完毕。

图3 球壳制造工艺流程图Fig.3 Flow chart of spherical shell manufacturing

表1 Q345R材料性能参数Tab.1 Material property parameters of Q345R

2.2 初挠度测量

采用Leica 激光跟踪仪AT401 进行试验模型初挠度的测量，基本流程是：首先在球壳外表面等距画出16 条经线和16 条纬线，测量经线、纬线交点处的空间坐标值，通过测量设备自带软件系统拟合得到球壳的球心坐标以及各点初挠度，见图4。初挠度测点数量为258 个，图5 为根据测量结果得到的试验模型初挠度云图，最大挠度为3.9 mm。提取四条经线上的测点数据进行分析，见图5，正值表示该测点处壳板沿径向外凸，负值为内凹。由图可知，焊缝两侧壳板明显向球内凹陷。这是由于焊接导致的角变形，使得焊缝及两侧壳板呈V字形，见图6。理论上，由于球壳赤道焊缝位于角变形的角点上，即V 字形尖端，该位置壳板的下凹幅度也应该是最大的。但是，由于焊缝余高的存在以及测量方法的局限性，一定程度上掩盖了壳板内凹幅度，使得焊缝处所测得的内凹幅度变小甚至转变为壳板外凸。

图4 初挠度测量现场Fig.4 The measurement field of initial defection

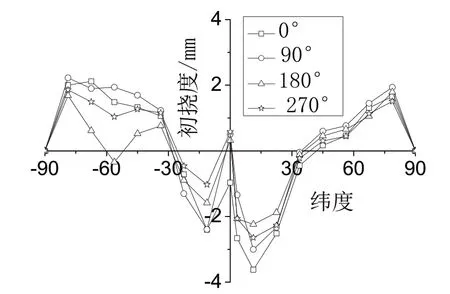
图5 90°经线初挠度测量结果 Fig.5 Measuring result of initial defection at 90°meridian

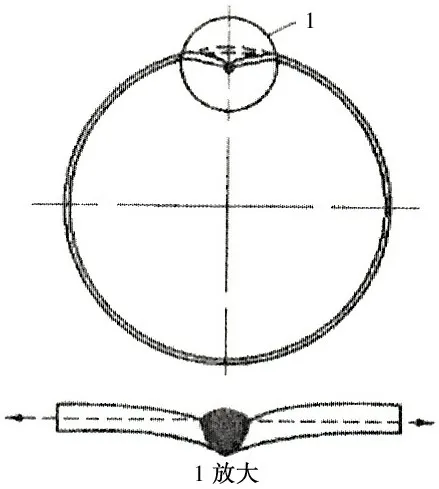
图6 典型焊接角变形Fig.6 Typical welding angular deformation

2.3 壳板厚度测量

采用超声测厚仪进行壳板厚度的测量，测量位置和测点数目与初挠度测量相同。为充分反应壳板厚度的分布规律，提取0°、90°、180°和270°四条经线上的测量结果进行分析，见图7，正值表示壳板增厚，负值表示壳板减薄。由图可知，四条经线上壳板厚度分布规律相同，均为两极小，中间大；局部位置出现壳板减薄现象，减薄量为0.2 mm。这一现象主要是由半球的制造工艺导致的。

2.4 残余应力测量

图7 厚度测量结果Fig.7 Measuring result of thickness

目前，常用的残余应力测量方法为盲孔法和X 射线衍射法，后者对被测试件损害最小。本文选用X 射线衍射法进行残余应力测量，测量设备为加拿大PROTO 公司iXRD 便携式残余应力分析仪，测试精度为±8 MPa，测试深度为10～30 μm（见图8）。

图8 残余应力测量现场Fig.8 The measurement field of residual stress

图9 测点位置 Fig.9 Measuring position

图10 残余应力测量结果Fig.10 Measuring results of residual stress

考虑到残余应力测量工作量大、耗时长以及球壳对称的特点，仅在某一条经线上0～90°纬度范围内选取测量点。残余应力测点位置见图9，沿经线分布，垂直于焊缝，距离焊缝横向距离为0mm 的点位于焊缝中心，距离为100 mm 的点位于焊缝右侧100 mm，以此类推。残余应力测量结果见图10，横轴表示测点位置，纵轴为应力值。图10 中数据点■为纵向（沿焊缝方向）残余应力σx，曲线a为其拟合趋势线，由图可知焊缝附近呈现较大的拉应力，最大为120 MPa；距离焊缝越远，应力越小，并逐渐转变为压应力，最大为-40 MPa；这一趋势与典型球壳赤道焊缝残余应力分布一致。数据点☆为横向（垂直于焊缝）残余应力σy测量结果，曲线b 为其拟合趋势线，总体规律与纵向应力相似，最大拉应力达到180 MPa，最大压应力为-15 MPa。但是，焊缝附近的横向残余应力较为分散，在20 mm 和50 mm 处出现较大的峰值。采用四次多项式针对测点数据进行拟合，可得残余应力与测点位置的关系式（5），可见残余应力分布与理论相符。

3 结果讨论

3.1 水压试验结果

为了得到试验模型的极限承载力，将试验模型放入大型压力筒进行外压试验，水压加载过程见图11，平均加载速率为0.14 MPa/min，当压力达到17.7 MPa时，压力筒内传来一声巨响，伴随着水压直线下降，由此认定试验模型发生破坏。模型破坏情况见图12，整体呈碗状，上半球完全凹陷并与下半球贴合，无裂缝出现。

图11 水压加载曲线Fig.11 Hydrostatic test trendline

3.2 基于实测数据的非线性屈曲分析

为了充分考虑实测初挠度、厚度和残余应力的影响，采用基于有限元软件ANSYS 的APDL 的二次开发程序，进行极限承载力计算。

考虑实测初挠度、厚度的有限元模型建立方法参考文献[11]，主要思路是先建立完善的几何模型并采用shell单元划分网格，然后根据实测的初挠度数值对相应的节点位置进行修正，最后根据厚度实测值修改相应shell单元相应节点的厚度值。为确保有限元模型球面的连续性、光顺性，采用四点插值的方法计算得出相邻节点的初挠度和厚度，然后逐个修正。

考虑到焊缝金属表面残余应力比内部小，而由于应力测定设备的限制，焊接接头内部的残余应力无法测量。为了提高计算的准确性，根据表面残余应力的分布规律外插得到材料内部残余应力的分布，见公式（6）。有限元计算采用拟合公式（6）进行残余应力的加载。公式自变量为x，表示某点相对焊缝（即0°纬线）的距离。显然，同一距离（纬度）上的节点处残余应力值相同。

图12 试验模型破坏情况Fig.12 Destruction of test model

采用弧长法进行计算，图13 为破坏压力下试验模型的等效应力云图，图14 为破坏位置径向位移压力变化情况，可知试验模型的极限承载力为19.0 MPa，破坏位置为焊缝上侧200 mm 处和上半球顶部，为局部屈服导致的失稳破坏。根据初挠度和残余应力测量结果可知，该区域初挠度较大，且为压应力区域。与水压试验结果相比，有限元计算结果与试验值接近，破坏位置与试验结果一致。

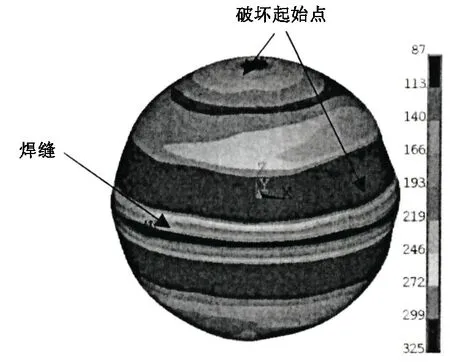
图13 破坏压力下球壳应力云图 Fig.13 Stress cloud chart under ultimate pressure

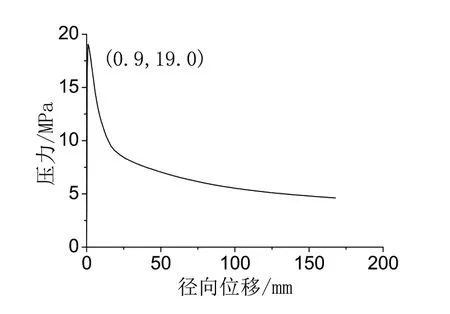
图14 破坏点径向位移随压力的变化Fig.14 Radial displacement change with pressure in failure position

3.3 计算方法对比分析

分别采用泰勒水池公式、俄罗斯公式和潘彬彬公式针对试验模型进行计算，结果见表2。考虑初始几何缺陷和残余应力后，有限元计算值与试验结果较为接近。泰勒水池公式和俄罗斯公式的计算结果均低于试验值，偏于保守，且球壳的所有非完善性因素均通过单一的衰减系数进行考虑，无法针对单一的影响因素（如残余应力）进行分析；潘彬彬等人的公式基于钛合金材料性能推导得出，对于钢制球壳具有一定的误差。非线性屈曲分析方法只考虑初挠度缺陷，根据特征值屈曲分析的模态进行初始缺陷的加载，因此，计算所采用的模态对结果影响较大[11]，模态缺陷形式不同，极限承载力不同，破坏形式也不同。

相比于以上方法，考虑初挠度、厚度和残余应力的非线性屈曲有限元法更加接近结构的真实情况，较解析法具有更强的适应性，最为重要的是，它可以粗略计算出实际结构的破坏位置。

表2 计算结果对比Tab.2 Calculation results of analytic methods

3.4 残余应力对极限承载力的影响

关于初挠度和壳板厚度对承载力的影响，目前已经过大量的研究并形成定论，而对于残余应力的影响还未有很多的研究。本文主要通过有限元计算的方法来讨论残余应力对承载力的影响规律。在初挠度和厚度分布恒定的前提下，采用上述ANSYS二次开发程序，分别施加不同的残余应力幅值计算球壳的极限承载力，结果见图15，图中σc为壳体残余压应力值，σs为壳体材料屈服极限，Pj为壳体极限承载能力理论计算值，P测为壳体极限承载能力的实测值，横坐标σc/σs表示残余压应力与材料屈服极限的比值，纵坐标Pj/P测表示极限承载力计算值与试验值的比值。可见，残余压应力对耐压球壳的极限承载力具有削弱作用，随着压应力幅值变大，极限承载力逐渐降低。需要指出的是，本文所采用的试验模型破坏形式为局部屈服导致的整体失稳，残余压应力的存在势必导致材料的提前屈服，从而削弱整体结构的承载性能。