基于系统辨识的大尺度模型耐波性试验实船响应外推预报

焦甲龙，孙树政，李积德，陈超核

（1.华南理工大学土木与交通学院，广州510641；2.哈尔滨工程大学船舶工程学院，哈尔滨150001）

0 引 言

常规的水池模型耐波性试验采用小尺度模型，波浪通常为长峰波，模型的运动由适航仪约束并测量，这些因素使得水池试验难以完全反映实船海上航行时的水动力特性。此外，水池长峰波试验会夸大船舶的运动与载荷响应，使船体设计偏于保守[1]。因此，研究船舶在短峰波中的响应是必要的。实船海试虽真实可靠，但实施成本高且周期较长。对于恶劣或极端海况下的实船耐波性研究，所期望的全尺度海况也是很难遭遇到的[2]。总之，实船海试有很大的局限性和不可控性。

基于上述状况，一些学者提出了实际海浪环境下大尺度模型试验技术。大尺度模型试验是指使用比水池模型更大尺寸的缩尺模型在自然水域中开展水动力学试验。通过大尺度模型试验可以得到三维海浪中船体的运动与载荷响应。该技术综合了水池试验和实船海试的部分优点，例如尺度效应小、风浪环境真实、模型航行范围广，且可进行任何浪向角下的试验。

国内外研究机构一般将大尺度模型试验用于重要型号舰船的设计定型。例如，美国海军驱逐舰DDG-1000 曾进行了45 m 长（缩尺比1:4）的模型试验，研究其运动性能、结构载荷及水下爆炸等。法国海军针对“夏尔·戴高乐”号航母开展了20 m 长（缩尺比1:12）的大尺度模型试验。希腊学者Grigoropoulos 等[3]提出了某大尺度舰船模型耐波性海上试验的步骤及方法。意大利学者Coraddu 等[4]在静水湖泊中开展了某舰船大尺度模型操纵性试验。孙树政等[5]针对两个大尺度模型在渤海湾开展了耐波性试验，并研究了试验结果与水池试验的差异。焦甲龙等[6]针对某舰船开展了缩尺比为1:25的大尺度分段模型的波浪载荷及水弹性试验。

大尺度模型试验中模型设计建造、试验实施方案、数据处理分析、综合性能评估等关键技术在文献[5-7]中已做了相关研究和报导。然而，大尺度模型试验技术目前还存在着一些尚未解决的难题，主要包括试验海况的选取原则和试验数据的实船响应外推方法。该问题可描述如下：即使对于相同浪级有义波高的海况，不同的波浪平均周期及方向分布也会对船舶响应造成一定的影响。然而自然海况中有义波高、周期、方向分布等参数是无法控制的，很难寻找到这三个参数同时满足要求的海况。因此，本文基于模型在某一工况下的测试响应采用系统辨识方法得到船型的固有响应函数，进而外推换算预报实船在其他任意海况下的响应。

1 大尺度模型试验技术介绍

现以某大尺度船模为例，对该试验技术进行简要概述。为研究某大型舰船的运动与波浪载荷性能，选取的模型缩尺比为1:25，模型水线长约12 m，排水量约4.6 t。将模型船体分成了七段，在第2、4、6、8、10 和12 站处将模型切开，用来测量该位置的剖面载荷。船模外壳由玻璃钢制作，在中和轴高度处安装柔性龙骨梁以测量剖面载荷，尾部一段的较大空间用于布置自航推进系统，模型总布置如图1所示。

为了实施真实海浪中的大尺度模型试验，采用的测试仪器设备主要包括浪高仪、高精度GPS/INS设备、动态数据采集仪、笔记本电脑、测量传感器（应变计、压力传感器和加速度传感器等）、电机及转速控制系统、自动舵设备、视频摄像仪等。

出于安全及可行性因素考虑，大尺度模型试验一般选在近岸海域进行。试验尽量选在遮蔽的海区并在涨潮时进行，这样可以避免涌浪的干扰。试验中模型的航行状态由辅助船上的人员远程控制，辅助快艇跟随模型共同行进并保持一定间距。在测量模型响应的同时还需测量试验海况，试验区域海浪采用浮标式浪高仪测量，模型遭遇海浪采用随船浪高仪测量。试验过程中主要改变三个控制变量：海况、航速和航向角。试验测量过程场面如图2所示。

图1 大尺度模型总布置图Fig.1 Large-scale model experimental setup

图2 大尺度模型试验实施场面Fig.2 View of large-scale model experimental campaign

2 试验海况换算及海域选取

船模水动力学试验是以相似理论为基础，将模型测试响应外推至实船。不规则波试验海况中的控制参数包括有义波高、特征周期和方向分布，本研究只考虑前两个因素。在水池模型试验中，波浪参数可在一定范围内任意组合选取，通过计算机控制的造波系统实现。然而自然海浪环境是不可控的，有义波高和特征周期很难同时满足期望值。本章将详细论述该问题，进而在下文提出由测量海况下模型响应外推其他海况下的实船响应预报方法。

2.1 试验海况的换算原则

船模水动力学试验中涉及到的相似准数为：雷诺数Re、付如德数Fr、斯特罗哈数St 和欧拉数Eu。对于惯性力起主要作用的耐波性实验来说，雷诺数和欧拉数不必完全相似。然而对于重力场下非定常周期性运动的船模运动响应研究而言，付如德数和斯特罗哈数必须严格相似：

式中：V为航速，L为船长，t为时间，下角标p对应实船，下角标m对应模型。

由（1）-（2）式可知，耐波性模型试验中必须满足的相似关系为

其中，λ 为实船与模型的线性几何尺度比。

在船舶耐波性研究当中，不规则波设计海况一般依据风浪等级选取，即根据目标船的类型及作业海域选取一系列风浪等级所对应的有义波高[8]。特征周期一般参考某海域的海浪长期统计资料，选取对应有义波高中出现概率最大或平均出现概率的周期。这样选取的原因在于实船航行时遭遇该海况的可能性最大，更符合实际情况。假设依据上述原则确定的实船海况有义波高为Hp，特征周期为Tp，由相似准则（3）式可以确定模型所对应的海况参数为：

2.2 问题的提出与描述

假设实船海况（有义波高Hp，特征周期Tp）在某一海区出现的概率为p( Hp,Tp)，考虑到大尺度模型试验的可实施性，则大尺度模型试验海况的出现概率p( Hm,Tm)也应尽可能大。换言之，在某海况长期分布表中，波高与周期的组合概率p( Hp,Tp)和p( Hm,Tm)都应为各波高中的最大值，这样才能同时保证研究的意义和试验的可实施性。

以中国沿海长期统计资料为例，其有义波高与平均周期的联合概率分布如图3 所示[9]。此外，出于普适性考虑，通过（6）式计算出的全球其他海域的波高与周期的联合概率分布也与图3相类似[10]：

图3 我国沿海海况波高周期长期统计资料Fig.3 Long-term statistical data of China coastal waves

式中，h 为无因次波高h = H/H0，t为无因次波周期t = T/T0，下角标0代表平均值，ε为谱宽系数。

将图3 中不同有义波高所对应的最可能出现的特征周期进行提取，并用线性回归拟合，结果如图4 所示。由此可发现，自然海况中波高与相应最大概率周期的关系可近似为一次函数。为了研究模型对应的自然海况换算至实船海况后波高与周期的对应关系，根据图4 拟合所得到的波高与周期一次函数关系式，结合（4）-（5）式可以计算出在自然环境下模型试验海况换算到实船尺度之后的海况信息。图5 给出了自然实际海况和不同缩尺比模型换算后实船海况的信息。由此可见，在某一波高下换算所得到的周期普遍高于实际周期，且随着缩尺比加大而迅速增高。即使在一些波高大于17 m 的情况下，换算海况可能与实际情况接近，但是这种大波高在自然界中很少见，不能作为普遍意义上的研究。然而需要说明的是，换算后的实船海况周期或波长较实际的自然值偏大，使得遭遇频率会更加接近船体的自振频率，这对于研究船舶在危险海况下的响应具有更强的指导意义。

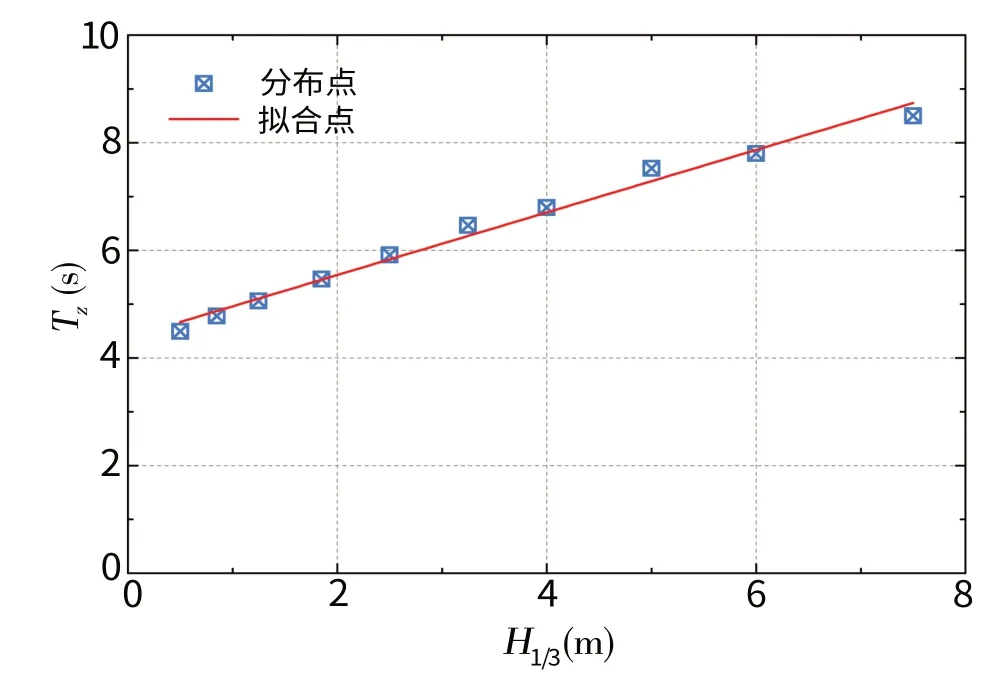
图4 波高与最可能周期分布 Fig.4 Distribution of H1/3 with most probable TZ

图5 不同缩尺外推下的实船海况Fig.5 Full-scale wave state at different scales

总之，模型试验的自然海况与换算后的实船海况很难同时满足要求，这也是大尺度模型试验技术中的关键问题。然而需要说明的是，上述研究仅限于对远洋中波高大于0.5 m 海况的统计分析，实际上近岸海浪参数随天气、地形和区域的变化范围较大。幸运的是，一些近岸遮蔽海区的小型风浪的周期较小，对于一些大比尺的模型而言，其波高与周期的联合分布换算到实船之后是满足要求的，例如文献[11]中的研究海况在换算之后就符合自然情况。焦甲龙等[12]也曾提出了大尺度模型试验海浪的选取方法。但无论怎样，提出一种具有普适性的由模型响应外推实船在其他海况下响应的方法是必要的，这也正是本文的主要研究内容。

3 基于时间序列分析的实船响应外推方法

为了将大尺度模型在某一测试海况下的响应换算至实船在期望海况下的响应，采用基于时间序列分析的NARMAX（带外生变量的自回归滑动平均）模型辨识出船舶的运动响应预报函数，进而外推不同工况下的船舶运动响应。

3.1 非线性时域模型

船舶在波浪中运动及载荷的流固耦合动力分析当中，存在着一定的非线性效应，特别是高海况下船舶的大幅摇荡运动。此外，流体对船体反作用力中存在着一定的记忆效应，可用运动微分方程表述如下：

式中，M 为船体质量，m 为流体附加质量，K( τ )为时间延迟函数，τ 为时间间隔，C 为船体静水恢复力系数，F( t )为波浪干扰力，x( t )为船体运动。

为了简化方程中的卷积项，经一系列推导可将（7）式简化为差分方程AR( l )自回归模型：

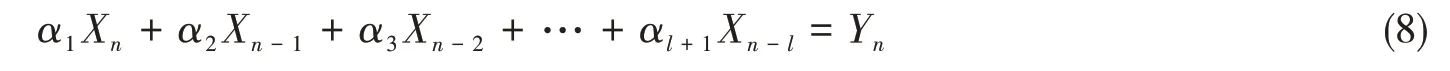
式中，αi( i = 1,2,…,l + 1 )为某系统的固定系数，Xj( j = n - l,n - l + 1,…,n )为系统j时刻的响应输出，Yn为n时刻的外界干扰，l为模型阶数。

为了更准确预报船舶的响应，在AR 模型中加入历史时刻的波浪输入信息，此外将系统噪声用白噪声序列表示，可以得到NARMAX模型：

式中，y( t )、u( t )和ε( t )分别为系统t 时刻的输出（船舶升沉、纵摇等响应）、输入（入射波浪等）和白噪声，ny，nu和nε分别为输出、输入和噪声的时间延迟步数，C为系统常数，d为时间滞后，ε( t )为残差。

3.2 船舶运动响应系统辨识

为了求解某船舶固有的时域响应预报方程，将（9）式展开为多项式，并改写为

其中，系数θm对于固定系统为固定值，多项式pm( )t 为输入、输出、噪声项以及它们的混合乘积项，M 为系统中的总项数。

为了辨识出系统的各个参数，需要给定一些已知的输入和输出信息，在此可理解为模型在某工况下测量的海浪输入与船模响应输出。若某已知数据包含N个时刻的测量值，可将（10）式写成矩阵形式：

该问题可转化为已知序列Y 和矩阵P，估计系统参数序列θ 使方程（11）残差最小，可通过最小二乘法进行求解。计算中使用向前回归算法[13]分别求解过程模型和噪声模型，具体算法及流程可参考文献[14]。在系统辨识中，对于低海况中的船舶响应可使用一阶线性模型，而对于中高海况则需使用二阶或高阶模型。在船舶响应外推预报中，由于残差序列是未知的，所以只使用过程模型即可。

3.3 不同工况下船舶响应换算

辨识出船舶的固有运动响应函数之后，即可根据其他任意输入海况对船舶运动响应进行外推预报，实船响应外推预报的整体思路及流程如图6 所示。需要说明的是，输入的艏前波浪时历应与船模响应同步对应，且应为遭遇波浪时历，船模响应信号可为运动、载荷、波动压力和加速度等。在船舶响应辨识过程中，可先使用一阶算法确定方程中的项数，再进行高阶辨识，直到通过模型检验为止。在进行船舶响应外推预报时，选取的浪向角应与已知辨识测试数据中的浪向角相同，因为不同浪向角下的船舶固有响应函数不同。

图6 实船响应外推预报方案Fig.6 Procedure of full-scale response prediction

4 算例分析与验证

以往开展的大尺度模型试验中尚未安装随船浪高仪，暂未得到艏前波浪数据。因此本章采用水池模型试验数据对上述外推模型进行验证，水池试验中波浪参数可控，更有利于检验所提算法的准确性。该外推模型一旦得到验证，对于水池试验、大尺度模型试验和数值计算结果处理均适用，其计算原理是相同的。

采用某单体复合船的水池模型试验数据进行分析，模型缩尺比为1:20，实船及模型的主尺度参数如表1所示，模型的安装如图7所示。试验在哈尔滨工程大学拖曳水池中进行，水池尺度为108 m 长、7 m 宽和3.5 m 水深。浪高仪固定在拖车上距船艏1.5 m处，试验中同步测量了入射波浪和模型升沉与纵摇响应，采样频率为100 Hz。不规则波试验波谱采用ITTC 单参数谱，选取了4 级（H1/3=2.5 m）和6 级（H1/3= 4.5 m）两个典型海况，有义波高对应模型分别为125 mm和225 mm。实船航速选取18 kn和24 kn，对应模型航速分别为2.07 m/s和2.76 m/s。

选取模型在6 级海况下以航速18 kn 迎浪航行时的波浪输入和模型响应输出为已知量，如图8 所示，以此辨识出模型的运动响应固有函数。进而分别外推预报船舶在4 级海况18 kn 航速和6 级海况24 kn 航速航行时的升沉与纵摇响应，并将预报值与试验测量值进行对比验证。

表1 船型主尺度Tab.1 Main dimensions of hull

NARMAX 模型中选用二阶非线性模型进行系统辨识，输入、输出和噪声的时间延迟步数分别取8，8 和10，升沉和纵摇的过程模型门槛值分别设为0.006 和0.01，升沉和纵摇与入射波浪之间的时间滞后数分别取28 和25，时间间隔为0.05 s。辨识结果如表2 所示，其中ERR 为误差缩减比，是衡量各项重要程度的参数。

图7 水池试验模型安装Fig.7 Experimental setup of a model in the tank

图8 六级海况下的已知数据（V=18 kn）Fig.8 The known model testing data under Sea State 6(V=18 kn)

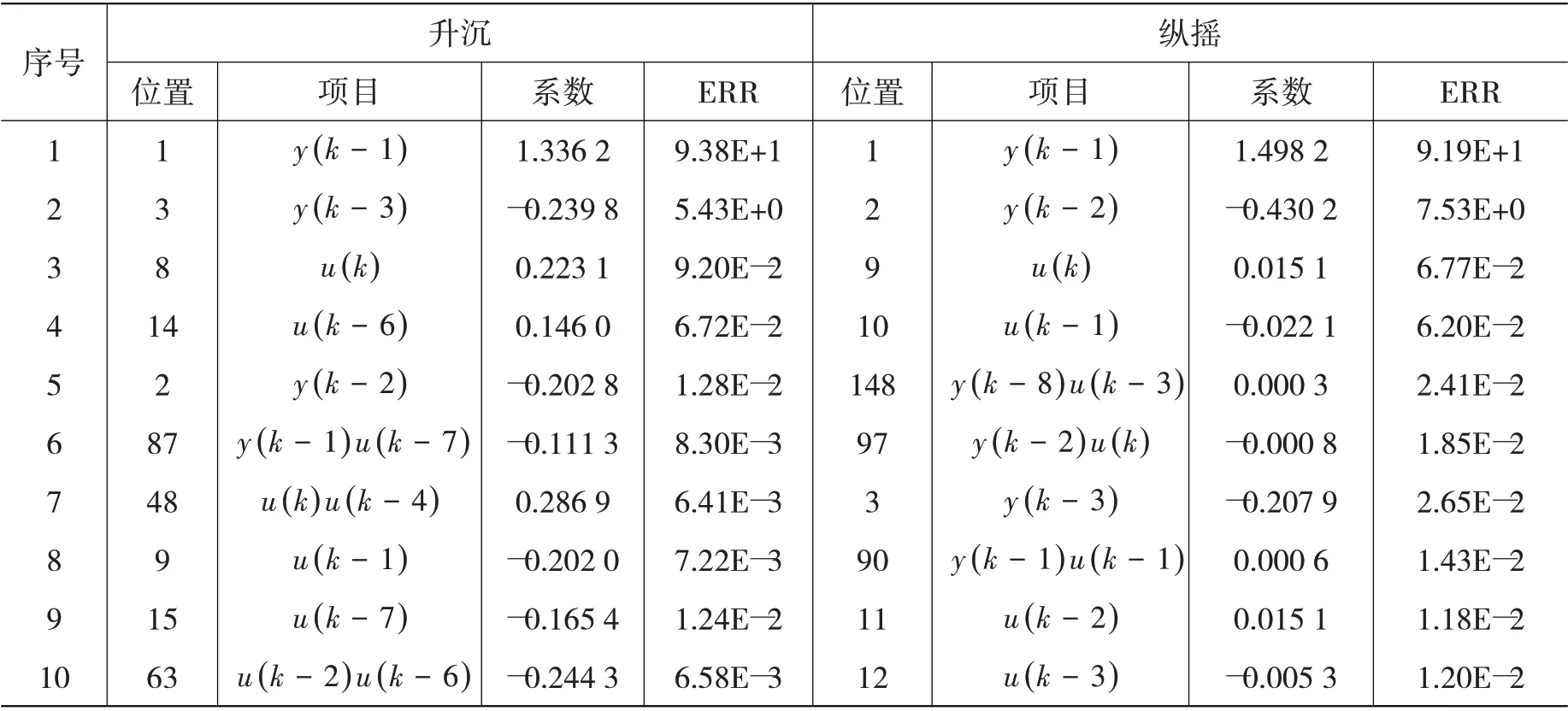
表2 辨识出的船舶响应参数Tab.2 The identified ship response coefficients

由此可知，船舶升沉和纵摇响应的函数表达式可分别写为（12）式和（13）式。图9 所示为所得非线性模型的相关性检验结果[14]，各曲线为变量间的相关函数，e代表误差，u代表输入。可以看出，各标准化相关函数曲线基本都落在置信区间带内，因此预报模型满足要求。

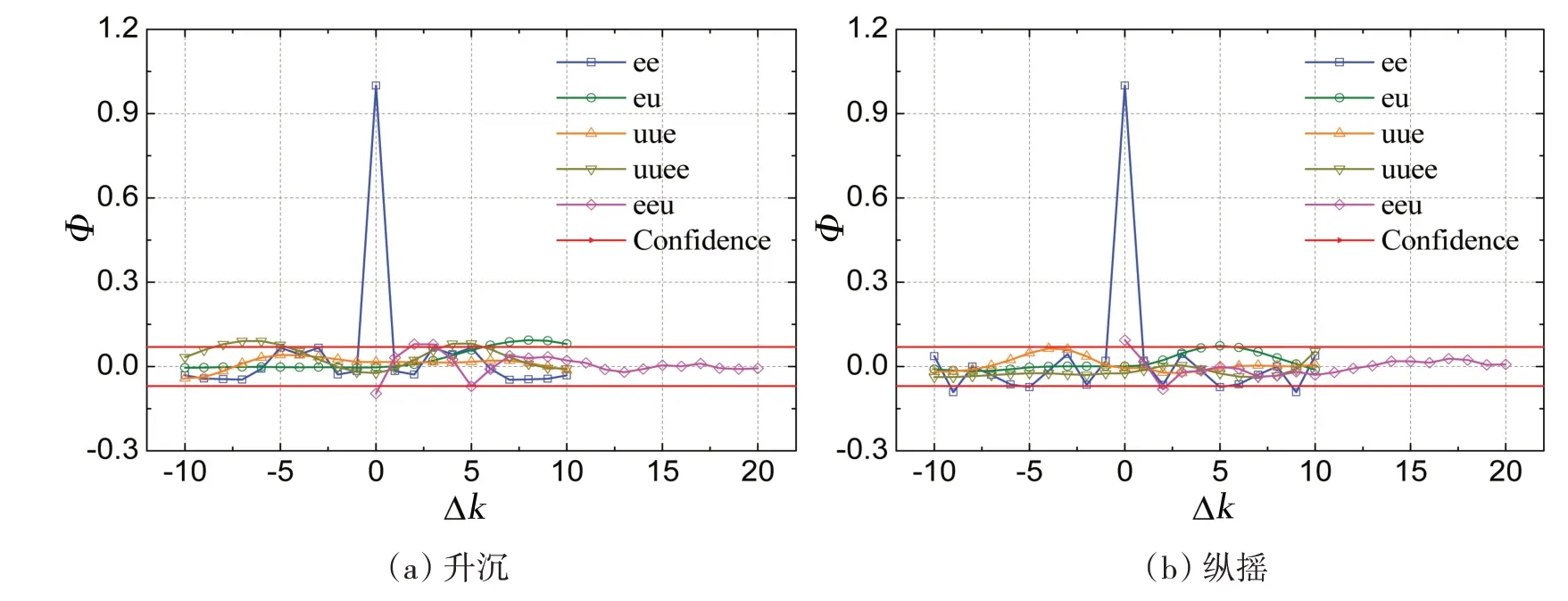
图9 相关性检验函数Fig.9 Correlation test function

图10 不同工况下的遭遇波浪时历输入Fig.10 Incident wave in different testing conditions

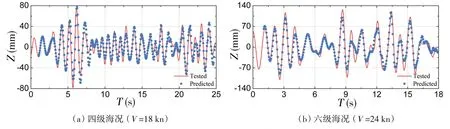
图11 不同工况下船模升沉响应预报值与试验值比较Fig.11 Comparison between prediction model heave value and measurement in different conditions

在不同工况下以入射波浪为输入，基于（12）式和（13）式外推预报船舶在相应工况下的响应。四级海况18 kn 航速和六级海况24 kn 航速时输入的遭遇波浪时历如图10 所示，外推预报出的相应工况下船舶的升沉和纵摇响应分别如图11和12所示。可以看出，外推预报的船舶响应与实测值的吻合度良好，完全满足工程应用需求，证明了本文所提方法的可行性。可以进一步推广为输入长时间的入射波浪时历，外推预报船舶的中短期响应，进而可根据所得时历进行有义值等统计谱分析，最后通过相似定理换算至实船即可。

图12 不同工况下船模纵摇响应预报值与试验值比较Fig.12 Comparison between prediction model pitch values and measurement in different conditions

5 结论与展望

本文首先阐述了大尺度模型试验中模型海况与实船海况换算中存在的限制因素，并为此提出了基于系统辨识的实船响应外推换算方法，解决了大尺度模型试验中一项关键技术问题。所提出的外推方法同样也适用于水池模型试验及数值计算中不同海况下的船舶响应的换算。通过算例分析表明，外推预报的结果与实测值吻合度高，证明了该外推方法的可行性。且该时域模型依据很少量短时间的已知数据即可辨识出船舶的固有响应函数，也不受航速的限制，避免了频域谱分析法中需要大量的长时间的测量数据。此外，通过非线性时域分析法，可以进一步研究舰船在高海况下的强非线性运动响应特征。

尽管本文解决了大尺度模型试验中一项关键难题，然而还有一些研究工作需要进一步开展。本文仅证明了长峰波中船舶升沉和纵摇响应外推结果的准确性，短峰波中运动响应和载荷信号预报的可行性还需进一步验证。本文所提船舶响应外推模型需要艏前波浪数据，因此大尺度模型上需要安装随船浪高仪，设计研发一套船艏安装浪高仪的稳定云台也是下一步要开展的工作。只有获取准确的入射波信息，才可以更精确地辨识出模型的响应函数。

本文对我国沿海海浪波高与周期联合分布的分析仅限于远洋中波高大于0.5 m海况的研究，然而近岸遮蔽海区的海浪参数随气候、季节、天气、风场、地形和区域的变化范围较大，因此对于近岸小浪高的周期分布还需进一步研究。焦甲龙等[12]分析了大尺度模型试验海浪的相似性并提出了海浪选取方案。尽管大尺度模型试验场区的海浪参数是无法控制的，但是实验设计中还是有可能通过选择试验海域和试验时间来获取目标海况。文献[15-17]介绍了我国沿海海浪有义波高和特征周期的时间和空间分布规律特征，这对于指导和帮助试验海区的选取有重要意义。