泥岩地层软化对反井扩孔井帮稳定影响分析
2019-12-25程守业龙志阳刘志强
汤 正,高 峰,程守业,龙志阳,刘志强
(1.煤炭科学研究总院建井研究分院,北京 100013;2.北京中煤矿山工程有限公司,北京 100013;3.煤矿深井建设技术国家工程实验室,北京 100013)
反井钻井法在众多地下工程领域已经取得了越来越多的应用,其成孔质量好,钻进效率高,既安全又环保,极大地改善了工作条件,成为地下工程领域重要的工艺技术。其中,导孔和扩孔是其施工工艺的主要部分:首先,在反井上口从上往下进行导孔,等到导孔钻头与下水平巷道贯通后,用扩孔钻头替换掉导孔钻头,由下向上进行扩孔,直到和上水平贯通[1]。
反井钻井法扩孔施工过程中,井帮缩径和井帮围岩失稳是反井钻井法发展的重难点问题。井帮缩径会导致无法放钻,不能进行钻头和滚刀的保养、维修和更换;井帮围岩失稳会导致井筒坍塌、埋钻等安全事故发生[2]。分析其原因是:反井钻井扩孔工程中,破碎岩渣下落,人员无法进入井筒对井帮进行支护,井帮裸露的时间长,从扩孔开始到扩孔结束,直到反井钻机拆除,大面积暴露的井帮容易发生风化、水化破坏。其中,当扩孔穿过遇水软化性岩石(如泥岩、石膏岩、泥质砂岩、页岩等)为主构成的地层时,水对井帮围岩的影响十分突出,这主要体现为水对该类岩石的力学性质和自稳能力的降低[3]。在实际反井钻井过程中,当井帮围岩为遇水软化性岩石时,会因为遇水而导致其力学性质变低,从而发生塑性变形产生位移,进而导致井帮缩径甚至失稳。
为了研究遇水软化性岩石的遇水软化特性,国内外学者作了很多方面的研究。周翠英等[4]通过研究软岩在浸水条件下的力学性质,发现该类软岩的抗压、抗剪强度均随着浸水时间呈现指数变化;Yoshida[5]分析了泥岩的软化特性并指出泥岩的力学性质随浸水时间增加而逐渐减弱;藤宏伟等[6]利用声波探测,得到了页岩的弹性模量、抗压强度和浸水时间的软化方程;任松等[7]通过正交试验研究了泥岩夹层浸水软化和浸泡时间、温度、卤水浓度的影响规律,得出了浸泡时间是对泥岩软化性质影响最大的因素,权重达到80%以上。
结合反井工程的实际需要,以重庆綦江蟠龙抽水蓄能电站取出的具有典型遇水软化特性的泥岩为研究对象,进行了泥岩的浸水软化试验,得到了泥岩的弹性模量、泊松比与浸水时间的定量关系,并基于弹塑性模型塑性区位移解,建立了考虑软化效应、边界效应的井帮围岩位移与浸水时间解析模型。该模型依据蟠龙抽水蓄能电站的实际工程地质情况,为反井钻井法的实际工程应用提供了参考。
1 软化试验
1.1 试样选取及加工方法
实验泥岩岩样取自重庆綦江蟠龙水电站。加工后的岩样试件为高100(±2)mm,直径50(±1)mm的圆柱体。共制作24个试件,分为8组,每组3个,第1组为未浸水试件,剩下7组为浸水试件。分别测出试件在未浸水,浸水4d、7d、14d、28d、40d、50d、60d环境下的轴向力、轴向位移、径向变形。浸水时间梯度见表1。

表1 泥岩浸水时间方案
浸水结束后,对试件进行单轴压缩直至试件完全破坏,试验的加载方法为位移加载法,加载速度为0.1mm/min。
1.2 试验结果及分析
根据实验测得的试件轴向力、轴向位移、径向变形,分别计算出泥岩未浸水、不同浸水时间下的弹性模量和泊松比,见表2。
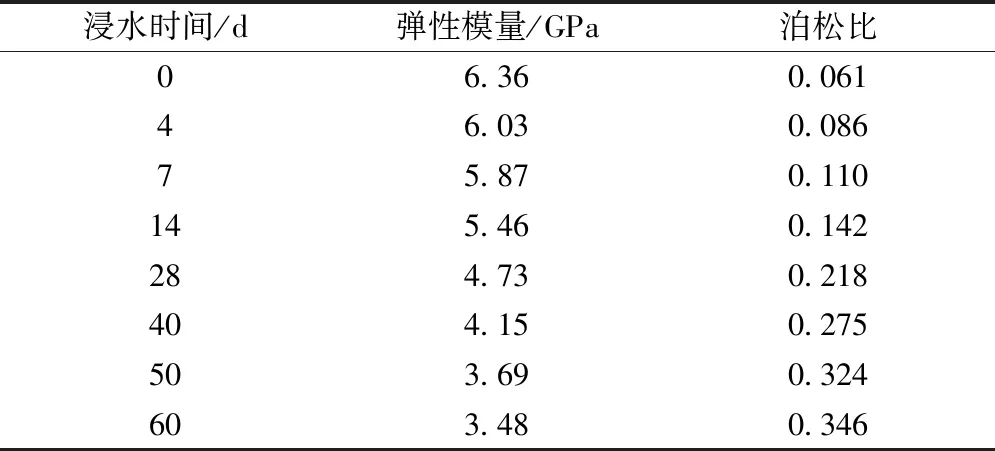
表2 泥岩浸水后的弹性模量和泊松比
泥岩岩样弹性模量随浸水时间的变化如图1所示。泥岩岩样的弹性模量随着浸水时间的增加逐渐下降。当浸水时间达到60d时,泥岩岩样的弹性模量已下降至3.48,减幅达到45.28%。这说明水对泥岩的软化作用很显著。为定量表征泥岩岩样浸水后弹性模量随浸水时间变化的表达式(设定泥岩完全软化后弹性模量接近于0),利用公式(1),用MATLAB对试验数据进行拟合。
Et=Ee-mt
(1)
式中,Et为t时刻的弹性模量;E为初始弹性模量;m为泥岩岩样的软化参数;t为浸水时间。

图1 泥岩弹性模量随浸水时间变化
泥岩泊松比随浸水时间的变化如图2所示。泥岩的泊松比随着浸水时间的增加而增加。为得到泥岩浸水后泊松比随浸水时间变化的定量表达式(设定岩石的泊松比不会无限增大),利用式(2),用MATLAB对试验数据进行拟合。
式中,μt为t时刻的泊松比;μ为岩石未浸水时的泊松比;n为泥岩岩样的软化参数。
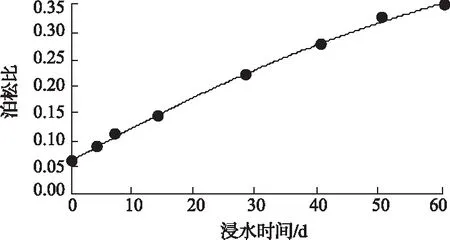
图2 泥岩泊松比随浸水时间变化
2 井帮围岩位移与浸水时间解析模型
在反井扩孔过程中,其钻进计算是一个三维的问题,但当井筒埋深较深时,其离地表远端的纵深方向的变形会受到限制,考虑到地应力随井筒深度的变化与地应力本身相比是一个小量,因此,将问题简化为平面应变问题。同时,由于井筒断面为圆形,其水平最大主压应力σH与水平最小主应力σh相等,即原场水平地应力为等向应力,因此将问题简化为圆形轴对称问题[8]。为建立解析模型,做出以下假设:①不考虑断层的影响,井帮围岩泥岩段按均质的、各项同性的连续介质来考虑;②本研究用岩石完整性系数K[9]来表示岩块的弹性模量和岩体的弹性模量之间的关系;③为简化问题,本研究不考虑水的分布情况,假设水对围岩的影响是一个完整的效果,用水影响因素S[10]表示;④设定反井扩孔过程中,井帮发生缩径的最大许用位移为ua,井帮围岩不发生失稳的临界位移为uc,井帮实际位移为u′,当ua
井筒未扩孔钻进之前,岩层存在一个初始地应力场,其可看做一个均匀的、等向的应力场,井筒开始扩孔钻进时,岩层产生附加应力场,井帮附加应力场的分析应属于弹塑性分析范畴。当岩层视为弹塑性体时,附加场作用于岩层可分为弹性变形阶段和塑性变形阶段:在弹性变形阶段,可利用厚壁圆筒的应力解和位移解(此时厚壁圆筒外半径与内半径的比趋于无穷大),可得反井扩孔钻进弹性变形阶段的位移、应力公式;在塑性变形阶段,井帮临空面为塑性区,由Tresca屈服准则、平衡方程、以及边界条件,可得,塑性区的位移公式[11]:
其中,u为井筒围岩内任一一点的位移;μ为围岩泊松比;E为围岩弹性模量;R0为井筒半径;σH为地应力,σH=γH,H为遇水软化类岩石埋深;r为围岩上一点到井筒中心的距离,本文研究井帮临空面的位移,取r=R0;λ为载荷参数,λe为弹性极限荷载系数[8],λ=λe时,井帮开始屈服。因此,取极限状态下井帮临空面上的位移,将式(3)转化为:
基于假设②、③,得出t时刻下,围岩浸水后的弹性模量和泊松比表达式:
E(t)=KEe-mst
(5)
式中,E(t)为t时刻围岩浸水后的弹性模量;μ(t)为t时刻围岩浸水后的泊松比。s=0时,表示无水状态,没有软化效应。s=1时,表示岩石处于浸水饱和状态。地下水对工程围岩的影响,按水量、岩石性质等因素,设置kw[12]作为水的影响系数,其取值见表3。基于s和kw具有相同的工程应用,本文中s与kw的关系表达式为[13]:
s=1-kw
(7)
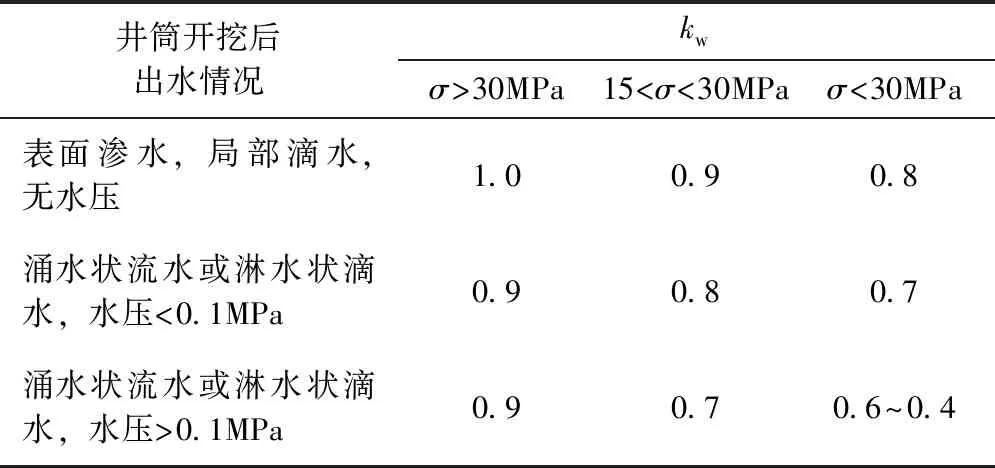
表3 kw的取值依据
注:σ为岩石单轴抗压强度,MPa。
将式(5)、(6)代入式(4),得到考虑围岩遇水软化效应的扩孔井帮临空面位移解:
实际工程中,破岩工作面对井帮临空面位移存在边界效应影响,其影响范围为l0,一般情况下l0=3D[14],D为井筒直径。设井帮临空面上一点到扩孔破岩面的距离为l,当l>l0时,位移不受破岩面影响;当l≤l0时,位移与l的关系为[15]:
式中,u′为距离扩孔破岩面为l处的井帮临空面上一点的位移。根据位移连续性,当l=l0时,u′=u。由此求得参数a的值。
由式(8)、(9)可得:
式(10)即为考虑边界效应的井帮围岩位移与时间解析模型,体现了井帮位移、时间及各参数之间的关系。公式中涉及的影响因素见表4。

表4 公式中涉及的影响因素
由假设④,当ua
3 工程应用
重庆綦江蟠龙水电站通风竖井采用反井钻井法施工,井筒围岩中有一段为泥岩,且该段围岩附近含有地下水。由地质勘探、现场数据反馈及泥岩软化实验,各参数取值依据如下:
1)井筒半径R0=2.5m,泥岩段埋深H=300m,上覆岩土容重γ取均值为24.8kN/m3,泥岩段岩体完整性较好,围岩影响因素k取0.8。
2)泥岩的单轴抗压强度为60~80MPa,地下水呈淋水状滴水状态,水压大于0.1MPa,由表3,取kw为0.9,则s=0.1。
3)参考Sakurai[16]判断围岩是否失稳的容许位移(围岩应变量大小)判据:应变是指围岩的变形值与开挖面直径之比,并认为2%是极限应变量,如果应变大于2%,将有发生围岩失稳的风险。取泥岩围岩不失稳的临界位移值u′=uc=100mm。
4)由泥岩软化实验,得出不同浸水时间下的泥岩弹性模量E和泊松比μ,同时,由数据拟合,得出m=0.011;n=147。
将各参数代入式(10),得到井帮位移与浸水时间的关系曲线,如图3所示。
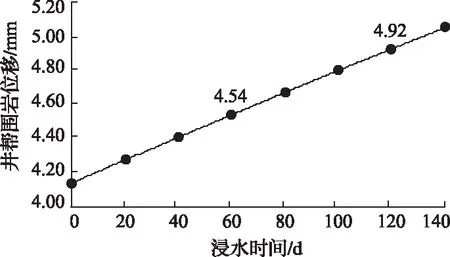
图3 井帮位移与浸水时间的关系曲线
对于该工程,反井钻机从泥岩段钻进至扩孔结束,共需要60d,参考图3,得出泥岩段埋深为300m的情况下,浸水60d的井帮位移为4.54mm,小于井帮缩径最大许用值;扩孔结束后至支护结束,共需要60d,参考图3,浸水120d的井帮位移为4.92mm,远远小于井帮围岩失稳的临界值。因此给出该段井筒扩孔施工的参考意见是:在扩孔施工段时间内,泥岩段围岩缩径值不影响放钻;扩孔结束至支护完成时间内,井帮围岩不会失稳。
4 井帮围岩位移与浸水时间解析模型参数自恰分析
基于表4中参数,代入不同的K值,得出泥岩完整性系数对井帮围岩位移的影响,如图4所示。
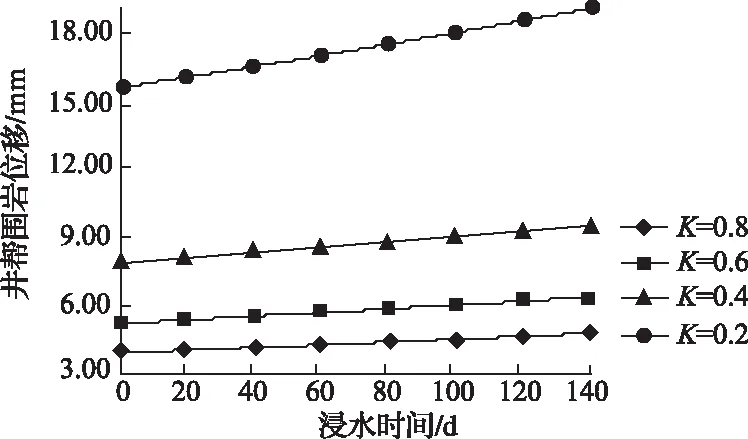
图4 泥岩完整性系数和井帮围岩位移的关系曲线
由图4可知,在其他因素相同的条件下,泥岩完整性系数越大,井帮围岩位移越小,由常识可判断,此结论是合理的。
同理,代入不同的H值、E值、s值,分别得出泥岩在不同埋深、不同弹性模量、不同水影响系数的条件下,相对应的井帮位移。如图5—图7所示。
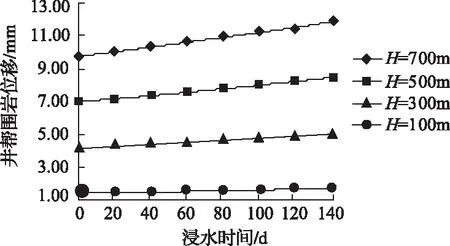
图5 泥岩埋深和井帮围岩位移的关系曲线
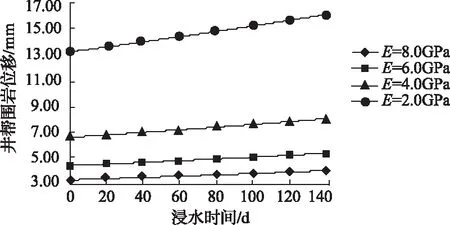
图6 泥岩弹性模量和井帮围岩位移的关系曲线
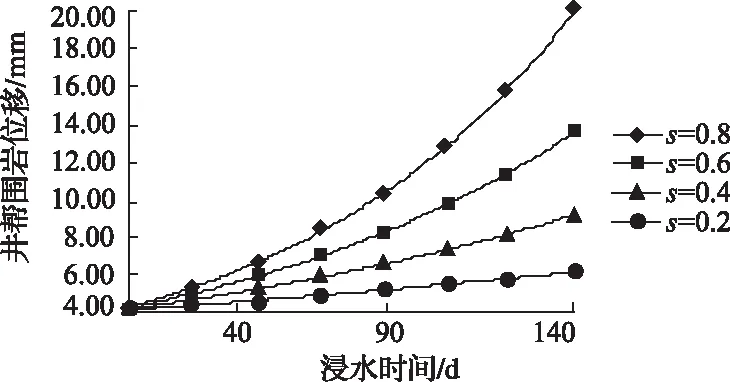
图7 水影响系数和井帮围岩位移的关系曲线
由图5可知,泥岩的埋深越浅,井帮围岩位移越小;由图6可知,泥岩的弹性模量越大,井帮围岩位移越小;由图7可知,泥岩的水影响系数越小,井帮围岩位移越小。结合实际情况,上述结论均是合理的,说明本研究的井帮围岩位移与浸水时间解析模型具有自恰性。
5 结 论
1)通过泥岩浸水软化试验,得出了泥岩的弹性模量随着浸水时间的增加而减小,泥岩的泊松比随着浸水时间的增加而增加。通过数据拟合,建立了泥岩弹性模量、泊松比和浸水时间的定量关系方程。
2)通过建立井帮围岩位移与时间解析模型,得到了考虑工程参数、岩石力学参数、软化特性、边界效应的井帮围岩位移和浸水时间的关系式。
3)通过自恰分析,得出了井帮围岩位移与各类参数的变化规律和实际情况相符,进一步验证了本文建立的井帮围岩位移与浸水时间解析模型的自恰性。
4)当反井工程通过遇水软化的地层时,通过井帮围岩位移与浸水时间解析模型,可以为实际反井钻井法的工程应用提供参考。
