缆松弛补偿器液压管路边界层厚度与温度耦合关系仿真分析
2019-12-25
(大连海事大学 轮机工程学院,辽宁 大连 116026)
在对液压系统故障的研究中,大多主要集中在故障诊断、故障定位及故障原因查找等方面,而对当前液压系统状态正常但存在故障隐患的预测研究较少[1]。对液压系统特征参数的提取主要利用单一的时域、频域和时频联合域指标构建特征向量,不能有效地反映故障信息[2]。且现有对液压系统运行状态的研究从宏观入手较多,大多通过利用硬件、软件对液压系统运行过程中的动态参数进行采集、处理,建立特征参量与故障类型的映射模型[3-7],或以传感器为基础研制检测仪[8-9]。研究工作主要是针对整机设备对液压设备状态进行评估,而对特定部件微观的状态评估研究较少。液压系统管路的宏观状态特性与微观的状态特性息息相关,可反映液压系统的实时状态[10]。因此,如果从边界层理论出发,并且将现有的MEMS传感器技术引入到船舶液压系统中,研究边界层与液压系统参数的关系,可实现大系统复杂信息感知领域的理论突破。
在众多需要监测并分析的液压系统特征状态参数中,温度的变化将显著影响液压系统的整体性能,而液压系统边界层状态在温度变化中起主导作用。因此,考虑基于传统船舶液压故障预测与诊断的理论,分析液压管路边界层与温度的耦合,为液压系统的故障预测和监测新手段提供理论支撑。
1 流动方案设计
所选管路在工作时,其允许的运动黏度范围为10~380 mm2/s。在FLUENT管路流动仿真中,对于不同的流动状态,应采用不同的管道内流动的模型。通过式(1)来计算该管道内流动情况的雷诺数,根据雷诺数来设置相应的流动模型。
Re=ρVd/μ
(1)
式中:V,ρ,μ分别为流体的流速、密度与黏性系数;d为特征长度,即管的直径。
管路流动研究采取控制变量法,对科考船绞车系统缆松弛补偿器液压系统正常管路中的边界层特性分析的具体方案见表1。

表1 层流情况下,不同运动黏度的管路流动方案
由管路参数、液压油参数和流动情况,根据式(1)求得各黏度对应的雷诺数和湍流-层流转变运动黏度为28.65 mm2/s。
2 FLUENT模型建立
利用FLUENT软件层流稳态模型对三维密封管道进行数值模拟。模拟遵循流体力学三大方程,即质量守恒方程 、动量守恒方程和能量守恒方程[11]。
为了符合实际工况,模型充分考虑了现实中缆松弛补偿器液压系统液压泵出口管路的布置,模型的管路直径采用58 mm,其尺寸是缆松弛补偿器液压系统液压泵出口管路的直径大小。运用三维建模软件SOLIDWORKS建立缆松弛补偿器液压系统液压泵出口管路的三维模型,见图1。

图1 液压泵出口管路三维模型
选取缆松弛补偿器液压系统部分液压管路,基于FLUENT中管路稳态流动分析,采用控制变量法,对正常缆松弛补偿器液压系统管路中的边界层特性进行分析,为后面研究提供参考值。该缆松弛补偿器液压系统液压站的主要参数以及L-HM46 矿物油型液压油参数分别见表2、3。

表2 缆松弛补偿器液压系统液压站参数

表3 L-HM46 矿物油型液压油参数
采用基于压力的稳态隐式求解器,根据设计方案,模型的雷诺数范围是1 098.2~1 647.2,所以选取层流流动模型。流场操作压力为工作压力。
根据模拟流场设置边界条件:假设液压油在管道内部不可压缩流动,采用速度入口边界条件,入口速度为1.136 m/s,方向为垂直进口,液压管的入口为完全均匀流动。出口条件采用outflow出口边界条件。壁面边界条件设置为绝热壁面。由于在液压系统中,液压油的黏度会随着温度的改变而改变,所以在材料属性设置中,不能简单的设置为常数。根据液压工程师技术手册[12]中,液压系统常用的矿物型液压油,当40 ℃时运动黏度小于135 mm2/s,且温度在30~150 ℃范围内,用经验公式计算得到不同温度时液压油的运动黏度。
(2)
式中:ν40为温度为40 ℃时液压油的运动黏度;n为指数,随液压油运动黏度变化,见图2。

图2 40 ℃时,液压油运动黏度与指数对应关系
由此得到液压油运动黏度与指数关系式。
(3)
通过式(3)得到所用液压油对应的指数为2.115 6。一般液压油最低工作黏度为14 mm2/s。根据式(3)描绘缆松弛补偿器液压系统选用液压油的黏温图,见图3。

图3 液压油运动黏度-温度
根据缆松弛补偿器液压系统选用液压油的黏温关系式,编写自定义函数(user define function,UDF)来实现液压油运动黏度随温度变化函数。
3 仿真结果分析
通过FLUENT模拟仿真计算,得到进口体积流量qV,in=2.999 364 7×10-3m3/s。出口体积流量qV,out=-2.999 372 4×10-3m3/s,以及进出口的体积流量差ΔqV=-7.688 631 2×10-9m3/s。相对流量差|ΔqV/qV,in|=2.563 4×10-6,当|ΔqV/qV,in|≤0.5%时认为质量守恒。
管道0.35 m处的截面情况见图4,从管道截面中心点沿径向方向(y方向)到管壁的流速,该区域是属于边界层发展阶段。

图4 从截面中心点沿径向方向的流速
图4显示出管道在该方向分布的流速,在管壁内流速为0,然后向着中心点逐渐增加,曲线形状呈抛物线状。由于该处是处于边界层发展阶段,所以边界层厚度小于半径,但随着管道流动,边界层厚度会逐渐增加。
管道出口截面流速分布见图5。对应的流动情况见图6。

图5 出口截面流速云图

图6 出口截面流速的变化情况
通过图5和图6可以看到,管道出口截面流速数值大小呈抛物线状,截面中心流速最大,然后沿径向方向逐渐减少,直到管壁处流速为0。由于出口处边界层已经发展完毕,流速最大在截面中心处,其符合圆直管流动的现实情况。通过该方案进行模拟管道流动,满足圆直管层流流动规律[13]。因此,可以通过该方案分析液压系统的液压管道在各种情况下的管道边界层流动情况。
3.1 边界层厚度
边界层的厚度是从物面(即当地速度为零的地方)开始,沿法线方向速度与当地自由流速度U相等的位置之间的距离。边界层由绕流物体头部起,边界层厚度是从零开始沿流动方向开始逐渐增大,见图7。

图7 边界层厚度示意
图7中x表示流体沿管道壁面流动方向,y表示壁面到管道轴心的距离。在离开壁面不远的地方,边界层内的速度就已接近于外部速度。为了方便对管道各截面的边界层进行研究和数据提取,定义边界层厚度为截面最大速度的99%处到截面流动速度为0处(即管壁处),计算公式为
L(x)=l|uy=0.99U
(4)
式中:L(x)为管距为x截面处的边界层厚度;l为速度为uy时的实时边界层厚度;uy为管道的第x截面的径向方向上,距管管道轴心距离为y处的流动速度;U为为第x截面最大流动速度。
3.2 边界层厚度与系统温度参数的耦合分析
38.4 ℃时管道前端的速度云图见图8、9。

图8 38.4 ℃时管道前端速度云图

图9 38.4 ℃时管道前端速度云图局部
由于各温度的管道前段速度云图规律相似,因此选择单个温度的管道前端速度云图作分析。可以看出,管道前端内的边界层速度都是在进口均匀速度流进后,随着流体向前流动。由于管壁的影响,来流速度在壁面处速度逐渐减少,并且在靠近管壁区间很薄的流体层中减少作用最严重,由此可见流动的速度梯度大。
由于不考虑液压油的压缩性,所以在管道内流体流动一定的距离后,管道的总流量不变,中心流速慢慢增加。由于流速增加,管道内的压力随着流动方向递减,见图10。

图10 管道内截面轴线速度矢量图
通过液压管道流动轴向速度的分布情况分析,获得管道流动边界层厚度情况。对于在液压管道内流动,在正常工况下,边界层厚度是随着流动方向慢慢增加。从图11中可以看到边界层厚度的发展呈近线性增长,并且在1 m后会增加减慢速度。从42.7 ℃,0.5 m内边界层厚度发展曲线为V=-0.02x2+0.030 5x+0.004 6,对于其他不同运动黏度,边界层厚度发展情况与图8近似。
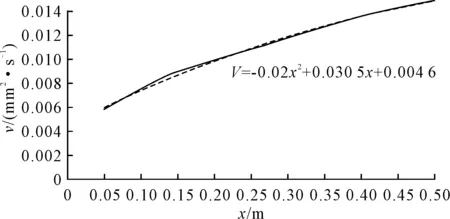
图11 42.7 ℃,0.5 m内边界层厚度变化
设计方案中5种不同管道液压油温度情况下(42.7~35.2 ℃),管道边界层厚度与管轴线方向距离的关系见图12。

图12 边界层厚度沿管轴线方向发展的变化
由图12可见,42.7 ℃温度下,边界层厚度增长速度最快。36.7 ℃温度下,边界层厚度增长速度最慢。图中显示边界层厚度的增长速度是随着管道液压油温度而变化,即管道内液压油温度的增大,边界层厚度增长速度也将会随之增大。因此,认为在液压系统管道边界层发展阶段区域,同一管道位置上,液压系统液压油温度与边界层厚度呈反比关系。同时,在管道边界层发展阶段区域中,液压系统液压油温度也与边界层厚度增长速度呈反比关系。
4 结论
通过仿真提取到液压系统温度与边界层厚度的耦合数据,分析得到系统温度与边界层厚度的关系。下一步可在实验中通过MEMS传感器提取边界层相关参数进行验证。此方法从边界层的参数出发,通过液压油管路边界层与系统参数耦合,寻找微观上的变化规律,实现对液压系统的状态的预测和提前诊断,从而提供一种实现对液压系统故障预防及提前诊断的新方法。
