基于四元数的机器人手眼标定算法*

王昌云， 李立君

(中南林业科技大学 机电工程学院，湖南 长沙 410004)

0 引 言

手眼标定的目的是求解机器人末端执行器坐标系到相机坐标系的变换矩阵，它是机器人完成手眼协调、自主导航等工作的基础。Tsai R Y等人[1]、Shiu Y C等人[2]将手眼标定的方程归结为AX=XB，并给出了其线性闭环解法，两种方法复杂且推导繁琐；王君臣等人[3]基于非线性优化解手眼标定方程，该方法精度高，但算法复杂且易陷入局部最优得不到最优解；文献[4～9]用矩阵直积等数学工具求解手眼标定方程，算法结构简单，精度有待提高。

本文利用四元数基于奇异值分解(singular value decomposition,SVD)手眼标定旋转部分，之后代入旋转部分的解求得手眼标定的平移部分完成标定。最后，将四元数的手眼标定方法(quaternion hand-eye calibration method,QCM)与文献[9]中的矩阵直积(matrix product)的标定方法进行对比实验，评价本文算法的优劣。

1 四元数的概念

1.1 四元数乘法

四元数向量可用来描述刚体的坐标旋转，设3个四元数向量分别为α=[a0,aT]T，β=[b0,bT]T和γ=[c0,cT]T，则两四元数相乘写为矩阵形式如下(乘法符号用“⊗”表示)

(1)

(2)

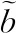
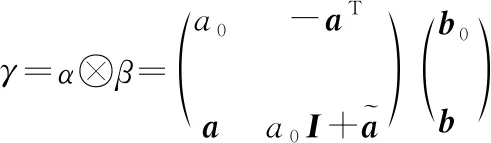
(3)

令

(4)

则式(3)可简写为

γ=α+β=β-α

(5)

1.2 四元数与旋转

单位四元数可定义任意两个坐标系之间的旋转变换关系，设任一空间向量r在坐标系Co，Ci和Cj中的表示为ro，ri和rj。任意两坐标系之间的旋转关系用四元数向量可表示为pio，poj和pij，则有

(6)

(7)

(8)

由式(6)～式(8)可得

pij=poj⊗pio

(9)

式(9)为四元数连续旋转的表达形式。

2 基于四元数的手眼标定求解

手眼标定方程AX=XB可解耦为旋转和平移2个部分。

RARX=RXRB

(RA-I)tx=RXtB-tA

(10)

式中R为3×3的旋转矩阵，t为3×1的平移向量。

2.1 手眼标定旋转矩阵求取

根据单位四元数表达连续旋转的特性，可将式(10)的等式一改写为

pA⊗pX=pX⊗pB

(11)

式中pA，pX，pB分别为旋转矩阵RA，RX，RB的四元数形式。结合上节所述式(11)可改写为

(12)

单位四元数向量p=[e0,eT]T和欧拉参数[θ,uT]的关系可表示为

e0=cos(θ/2)

(13)

e=sin(θ/2)u

(14)

综合式(13)、式(14)将式(12)改写成矩阵形式

(15)

式中θ为机械臂末端移动旋转分量的旋转角度，可人为控制。uA,uB为旋转矩阵RA和RB的旋转轴向量

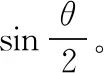
(16)

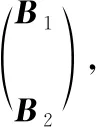
(17)

由式(17)即可求得pX特解。

2.2 手眼标定平移向量求取

将四元数pX转换成旋转矩阵RX并代入式(10)中，且机械臂存在2次移动则

(RA1-I)tX=RXtB1-tA1,(RA2-I)tX=RXtB2-tA2

(18)

式(18)中仅有tX为未知量，则令

(19)

由最小二乘法可得

tx=(CTC)-1CTD

(20)

3 实验与结果分析

3.1 数值模拟实验

该实验的硬件平台为CPU主频为2.7 GHz,内存为8 G的计算机，软件平台为MATLAB 2016a。

数值模拟分析的步骤如下：

1)随机生成3×3正交矩阵RX和3×1向量tx，作为手眼矩阵X的真实值；

2)随机生成正交矩阵RAi和tAi，i=1,2…N；

3)基于AX=XB求解RBi和tBi，i=1,2…N；

4)加入高斯噪声，模拟实际测量数据，考虑到旋转分量和平移分量的误差水平不同，参考王君臣在文献[3]的数据，对RAi和RBi加入均值为0，标准差为0.01d的高斯噪声，其中d为噪声水平；对tAi和tBi加入均值为0标准差为0.2d的高斯噪声向量；

5)对包含噪声数据的[RAitAi]和[RBitBi]分别使用文献[9]中的基于矩阵直积的手眼标定方法(matrix Kronecker-product hand-eye calibration method,KCM)和本文提出的QCM分别进行手眼标定。

为更好模拟实测数据，将上述标定过程重复1 000次(取N=20)，每次加入同分布但不同数据的噪声，标定结果用相对旋转误差和相对平移误差2个指标评价,即

(21)

(22)

至此，完成噪声水平为d的2种算法的相对误差估计。令噪声水平d=1,2,…,10，对每种噪声水平重复上述步骤，可求出两种算法在不同噪声水平的估计误差分布。模拟结果如图1所示。

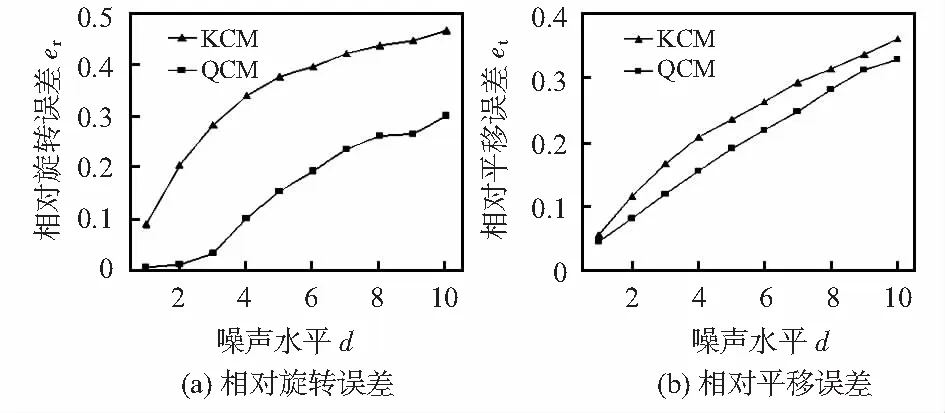
图1 两种误差与噪声水平的关系

图1(a)和图1(b)分别为两种标定算法的相对旋转误差和相对平移误差随噪声水平变化的关系图，从图中可得，随着噪声水平的增大，两种算法的相对平移误差和相对旋转误差都随之增大；在同等噪声水平下，本文算法的误差增长较低，稳定性更好。

3.2 机器人手眼标定实验

为了验证算法的有效性和精度，对机器人进行手眼标定实验。试验用机器人为自主研发的六自由度串联机器人，相机为维视MV-VEM120SC工业相机。

图2 机器人手眼标定实验场景

实验过程如下：机械臂移动N次，通过摄像机标定获取标定板与摄像机的N+1次位姿关系，通过机器人的控制系统获取机械臂末端和机器人基坐标的N+1次位姿关系。通过相邻两次位姿关系获取矩阵Ai和Bi。

通过文献[9]的KCM和本文算法(QCM)求取手眼矩阵X。误差定义为

(23)

实验取N=10，机器人手眼标定的误差结果如下：本文算法的手眼标定误差为0.123 8，基于矩阵直积的手眼标定误差为0.133 9。结果可得本文提出的基于四元数的手眼标定算法比基于矩阵直积的标定手眼算法误差低，标定结果更精确。

4 结 论

1)本文利用四元数表示坐标系在空间的旋转运动，基于SVD的线性优化算法和单位四元数特性求解手眼关系的旋转部分，代入平移部分等式基于最小二乘法求解手眼标定的平移部分。

2)数值模拟结果表明:本文算法相较KCM对噪声的敏感度低，稳定性高；机器人实验结果表明，本文算法有较高的精度，可满足机器人的应用需求。