磁场耦合双梁压电振动俘能器响应特性研究*
2019-12-24张旭辉谭厚志樊红卫
张旭辉, 左 萌, 谭厚志, 樊红卫
(1.西安科技大学 机械工程学院,陕西 西安 710054;2.陕西省煤矿机电设备智能检测与健康维护重点实验室,陕西 西安 710054)
0 引 言
随着微电子制造技术和无线传感技术的发展,微电子设备、无线传感器及各种新型电子产品的应用范围不断扩大,电子设备能量供应问题日益突出[1,2]。传统电池对于微型电子设备而言体积较大,供能时间短,能量有限[3]。环境中的机械振动最为常见且受环境因素影响较小[4],通过振动能量转换供能替代传统电池具有广阔应用前景。近年来,振动能量收集技术发展迅速,成为了当前热门的研究领域之一[5]。压电式振动能量采集器具有结构简单、能量转换密度大、与微机电系统(micro-electro-mechanical system,MEMS)集成容易等优点,是目前应用最广泛的振动能量收集方式[6,7]。
振动能量收集系统谐振频率与外界振动频率相同时系统产生共振,此时能量的收集转换效率最高[8]。典型的压电梁式能量收集器属于线性谐振系统,难以与实际振源频率相匹配,能量转换效率低,因此拓宽振动能量收集系统的谐振频带范围,提高能量转换效率成为主要研究目标之一[9,10]。朱莉娅等人[11]提出一种自调谐宽频带压电振动发电机,利用同步开关控制电路实现结构频率与实际振源频率相匹配,频率调节相对变化率达到5.1 %。本课题组前期提出一种线形—拱形组合梁结构俘能器[12]实现了多方向与自调谐俘能,提高了俘能效率。吴义鹏等人[13]提出共振频率可调式非线性俘能器,通过调节磁间距能够实现系统谐振频率与实际振源频率的匹配。王光庆等人[14]提出一种带有弹性放大器的悬臂梁式俘能器,通过分析俘能器性能表明弹性放大器谐振频率与压电梁谐振频率相近时,能够拓宽俘能频带。岳喜海等人[15]设计了一种多向宽频磁电式俘能器,借助磁场耦合实现多向宽频振动俘能。Mann B P等人[16]设计了一种具有双稳态特性的非线性俘能器,利用磁体间相互作用来拓宽能量采集器的频率带宽。周生喜等人[17]提出一种磁耦合式双稳态压电振动能量收集器,研究结果表明,该双稳态结构拓宽了有效频带,增大了输出电压。Andò B等人[18]提出了一种双稳态非线性振动俘能器,利用梁在两种稳态之间的转换冲击压电元件实现能量转换。研究表明,利用双稳态特性能够提高俘能器性能。姚丙盟等人[19]对双稳态能量收集系统进行研究,结果表明系统在合适的磁铁距离下具有双稳态特性,这种特性拓宽了系统的频率响应范围,使系统的能量转换效率提高。
本文以双梁—永磁体结构的压电振动俘能器为研究对象,基于磁偶极子理论建立磁力表达式,构建系统动力学模型并进行数值仿真,实验研究耦合磁场条件下悬臂梁响应特性以及水平磁间距对系统输出的影响规律。
1 系统结构建模及数值求解
1.1 模型建立
如图1所示为双悬臂梁结构的压电振动俘能装置。
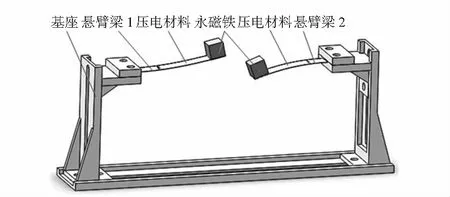
图1 双梁压电振动俘能装置
悬臂梁1与悬臂梁2分别固定在基座上,永磁体质量块位于悬臂梁自由端,压电材料分别粘附于两个悬臂梁上表面距离自由端10 mm位置。双梁长度不等,因此谐振频率不同,当其中任一个梁谐振频率与外界激励频率相匹配时将产生大幅值运动,系统中的磁斥力进一步增大运动幅值,拓宽大幅运动频带范围,另一个梁受耦合磁场影响也将产生大幅运动,从而实现系统俘能频带范围的拓宽。
1.2 永磁体非线性磁力建模
双梁压电振动俘能装置由两个长度不等的悬臂梁组成,由于引入磁场因素,首先对磁场部分建立非线性磁力模型,如图2所示。在悬臂梁上下摆动的过程中,永磁体的实际运动会以悬臂梁固定端为中心与水平面偏转一定的角度,由于偏转角度较小,在建模过程中忽略永磁体实际偏转角度,视为上下平行运动。
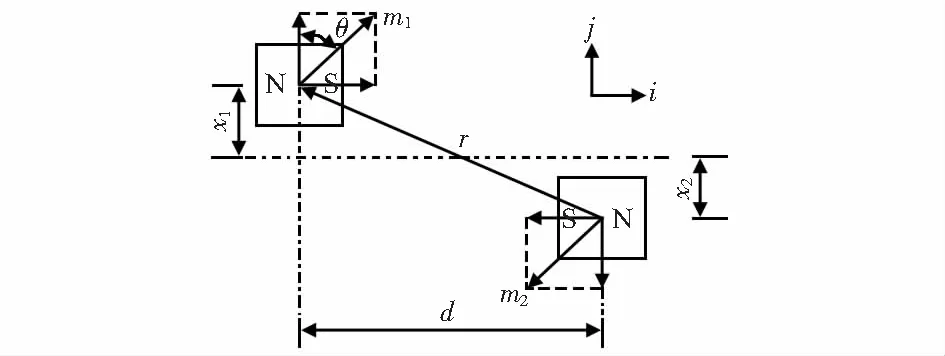
图2 磁力分析模型
为便于非线性磁力计算,将结构中的永磁体近似看作是磁矩分别为m1,m2的磁偶极子[20],其相对静止时的平衡位置的位移分别为x1,x2。磁矩m1,m2与j方向的夹角为θ,永磁体间距为d。经过推导可以得到永磁体的相互作用力Fm的计算公式
(m1·m2)·r-(5(m1·r)(m2·r)/r2)·r]
(1)
式中m1=M1V1(isinθ+jcosθ),m2=M2V2(isinθ+jcosθ),M1,M2分别为永磁体1和永磁体2的磁化强度,V1,V2分别为永磁体1、永磁体2的体积,μ0=4π×10-7H/m为真空磁导率,r=-di+(x1-x2)j为永磁体2到永磁体1的方向向量,r为向量r的模。
由于在悬臂梁振动过程中j方向上的磁斥力为主要影响因素,因此在计算中考虑j方向上的磁斥力,式(1)经简化得到j方向上的磁斥力大小为
(2)
将式(2)在(x1-x2)=0处泰勒展开,得到三阶磁斥力
(3)
永磁体间距d足够大时,磁体之间作用力近似为零,此时系统为线性系统;间距d减小到一定程度时,两个永磁体之间产生磁力,此时系统为非线性系统;间距d过小,则磁斥力过大,双悬臂梁的响应将受到抑制。
1.3 动力学建模
双梁压电振动俘能器在外界激励作用下,系统受迫振动,设悬臂梁1和悬臂梁2末端永磁体的振动位移分别为X1,X2,当悬臂梁以一阶模态运动时,可将系统简化为弹簧—阻尼的集中参数模型,如图3所示。
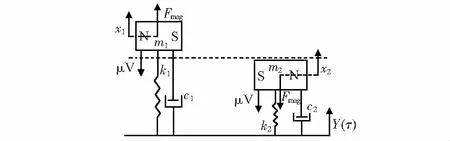
图3 集中参数的压电悬臂梁等效模型
压电式悬臂梁振动俘能器的控制方程可以由两个相关的物理量来描述成一个简单的数学模型。这两个物理量分别是悬臂梁末端永磁体位移X1,X2和输出电压V1,V2。这些物理量都是随时间变化的函数,并且遵循运动方程。根据牛顿第二定律和基尔霍夫定律,可以得到图3所示系统的动力学模型[21]
(4)
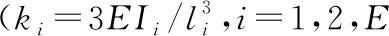
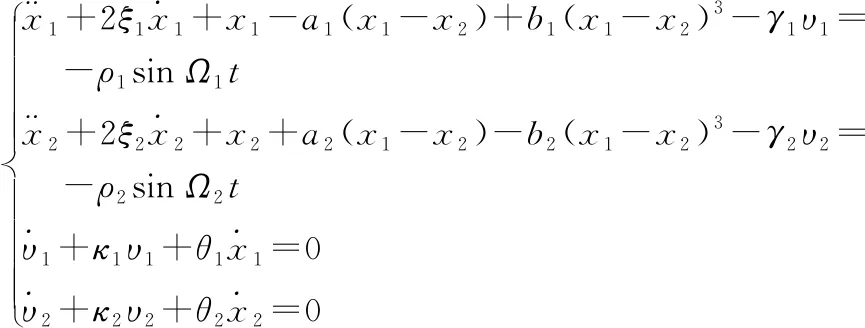
(5)
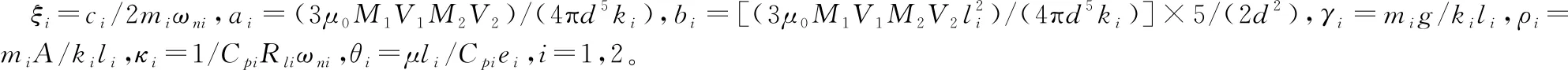
1.4 模型参数
模型的实际尺寸和材料参数如表1、表2所示。
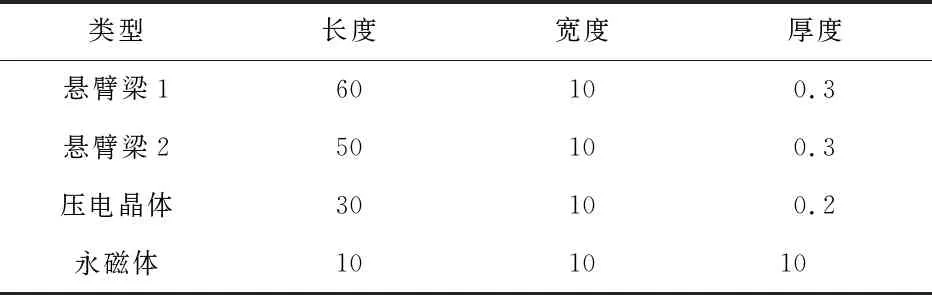
表1 结构尺寸参数 mm
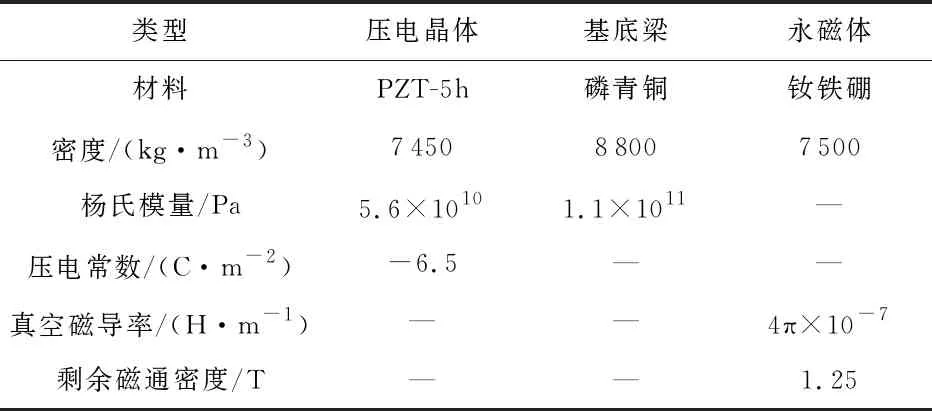
表2 结构材料参数
2 仿真分析
通过四五阶龙格库塔算法对无量纲动力学方程组(5)进行数值模拟,分别获得系统线性和非线性条件下的响应频谱特性。
如图4所示为悬臂梁1的数值解析结果,图4(a)为归一化位移频谱特性曲线,图4(b)为归一化电压频谱曲线,归一化后1号悬臂梁对应谐振频率为1。由图可看出,系统中不存在耦合磁场时,系统为线性谐振系统,其响应频谱图只有单一峰值。当系统中加入永磁体后,由于非线性影响系统响应出现双峰值现象,1号悬臂梁有效俘能频带数增加。
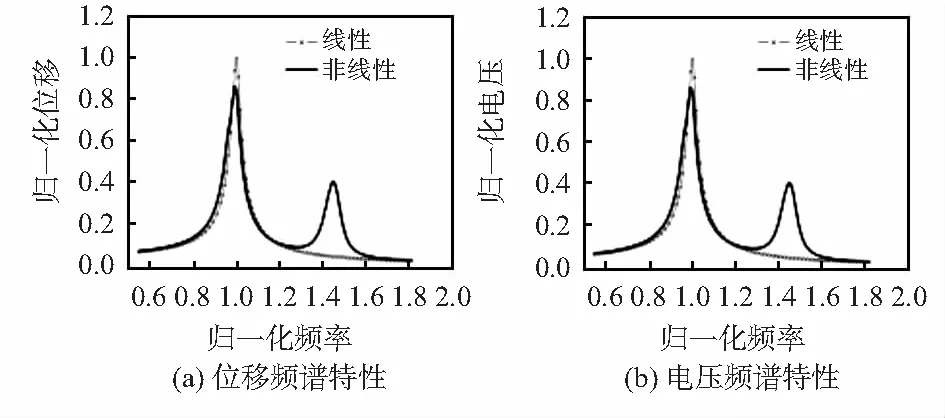
图4 悬臂梁1响应频谱特性对比
图5为悬臂梁2仿真结果,图5(a)为梁的归一化位移频谱特性曲线,图5(b)为归一化电压频谱曲线,归一化条件下悬臂梁2的谐振频率为1.45。由图中可以看出,与梁1响应情况相同,线性梁的响应频谱图只有单独的峰值,引入永磁体后,响应特性曲线呈现两个不同频率对应的峰值,悬臂梁2的有效俘能频带数增加,达到了拓宽俘能频带的目的。
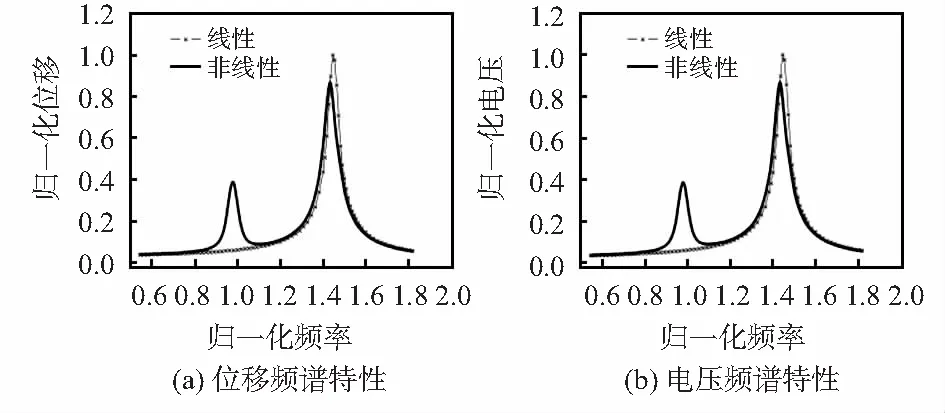
图5 悬臂梁2响应频谱特性对比
3 实验分析
3.1 实验平台
实验平台由振动控制台、功率放大器、激振器、双梁压电振动俘能器、激光测振仪、加速度传感器和PC组成。实验中采用非接触式测量方法,利用激光测振仪对俘能器响应位移幅值进行测试,避免加速度传感器在实验中因接触对测试结果的影响。
本实验通过改变永磁体间距,测试双悬臂梁俘能系统中永磁体对俘能系统输出的影响规律。实验首先测试在无磁场环境即线性条件下,悬臂梁式俘能结构的输出特性,分别确定两梁的固有频率,然后测试不同永磁体间距d=30,26,22 mm下的系统响应。
3.2 实验结果
选择激励源振动幅值为2 m/s2,分别测得悬臂梁1与悬臂梁2在无磁铁和不同磁间距下的响应位移频谱特性和输出电压,如图6所示。
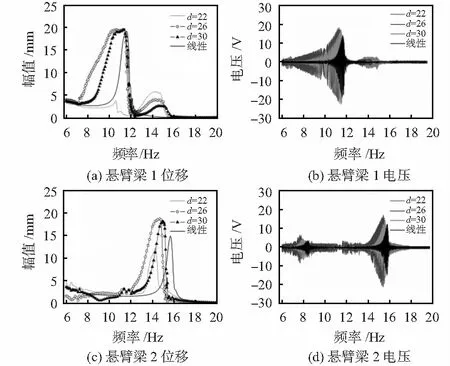
图6 不同磁距条件下响应位移和电压幅频特性
图6(a)和图6(b)分别为悬臂梁1的位移和电压响应特性,图6(c)和图6(d)是悬臂梁2的位移和电压响应特性。由图6(a)和图6(b)可看出,线性条件下,梁1谐振频率为11.8 Hz,带宽为1 Hz,对应位移峰值约为18 mm,输出电压约为14.6 V。系统加入耦合磁场后, 悬臂梁1的响应特性曲线出现2个峰,其主峰值对应谐振频率降低1 Hz,谐振频带宽度随磁间距的减小而增加,但由于磁间距d=22 mm距离太近,磁场势能大抑制悬臂梁的振动,此时系统响应幅值减小。次峰值由于磁场耦合而产生,且随磁间距缩小峰值增加。磁间距d=26 mm时系统响应效果最好,主峰值对应频带宽度较线性条件拓宽3 Hz,输出电压较线性条件提高约36 %。
由图6(c)和图6(d)可以看出,悬臂梁2的固有频率为15.8 Hz,带宽1 Hz,对应位移峰值约为15.6 mm,输出电压约为12.1 V。与悬臂梁1情况相同,加入耦合磁场后俘能器响应特性曲线产生两个峰值,主峰值对应频率降低,带宽随磁间距的减小而增加。次峰值产生在11.8 Hz,图6(c)中峰值不明显,但图6(d)中该段电压值明显增加。磁间距d=26 mm时系统响应主峰值拓宽2 Hz,输出电压较线性条件提高约40 %。
实验夹持装置采用3D打印制作,在激励频率8 Hz时振动明显,后续研究中将采用金属夹持装置。
3.3 误差分析
对比发现,双悬臂梁俘能器响应输出实验结果与理论结果存在误差,但整体趋势一致。通过分析,误差来源于:1)本文中采用压电陶瓷作为发电元件,材料不一致性及其与基底梁粘合产生误差;2)实验中夹持装置采用3D打印而成,振动传递一致性对实验结果有影响,后续考虑采用金属结构装置增大刚度。
4 结 论
1)建立集中参数的俘能系统模型,能够表达出双梁俘能器的振动响应特性,对加入耦合磁场后系统产生双峰值的响应预测效果良好;
2)悬臂梁式俘能结构中加入耦合磁场能够拓宽悬臂梁的谐振频带,频带范围由原来的单频带增加为双频带,有效俘能频带宽度最大拓宽为原来的3倍,电压输出明显提高;
3)双梁压电振动俘能器在耦合磁场作用下各悬臂梁的响应峰值由单峰值增加为双峰值,增加了俘能范围,随着磁间距的缩小,悬臂梁的主谐振频率降低,频带宽度增加,输出电压增高 ,但磁间距过小将抑制悬臂梁的振动。
