电动汽车动力电池包模态分析及优化

刘立邦，周长峰，张家豪

(山东交通学院汽车工程学院，山东济南 250357)

0 引言

电池包作为电动汽车固定动力电池的载体，在动力电池、电气系统安全工作和防护方面起着至关重要的作用，其结构的可靠性及安全性非常重要[1]。动力电池包与车架或车身相连，受到由车架或车身传来的振动冲击，因此动力电池包在满足静力学要求的同时，也要满足振动、冲击等动态性能的要求[2]。车辆行驶时，来自路面的激励频率一般为0～20 Hz[3]，考虑到其他激励作用[4]，如传动系统、车身、车桥的振动等[5]，通常电池包受到的主要振动激励频率均小于30 Hz。为防止产生共振，电池包的固有频率应避开常见的激励频率，否则，在车辆行驶时极易产生共振，使结构发生异响，影响车辆的乘坐舒适性，严重时还会引起零部件断裂失效[6]。

常采用模态分析研究电池包的振动特性。模态分析[7]是研究结构动态特性的一种方法，一般应用在工程振动领域，可用来确定结构的共振频段，并得到该频段激励下的振动响应。利用有限元软件，对动力电池包进行模态仿真，能够得到其固有频率及振型。

实际情况中，低阶模态很容易被外界激励，因此应避免常见激励频率与低阶固有频率重合。对于一阶固有频率过低的电池包，应对其结构进行优化，提高一阶固有频率，使其高于激励频率[8]。形貌优化是一种先进的优化形式，可在薄壁结构中快速确定加强肋的最佳布局，通过定义零件的设计区域，将设计区域细分为大量的独立变量，经过一系列迭代计算优化，在指定的设计区域内生成形貌优化模型[9-11]。

本文对某款电动汽车的动力电池包进行模态仿真，得到其固有频率及振型。为了使其固有频率避开外界激励频率，利用OptiStruct对电磁包箱盖进行形貌优化，确定加强肋的位置[12]，从而避免电池包使用过程中出现共振现象。

1 电池包有限元模型

本文分析的电动汽车动力电池包由3根横梁、2根纵梁、2块底板、箱盖及吊耳组成。该电池包所用材料为6061铝合金，其横梁、纵梁及底板采用挤压成型工艺制成，其箱盖为钣金件。电池包内部结构及几何模型如图1所示。

a)内部结构 b)几何模型图1 电池包结构及几何模型

1.1 有限元模型

在有限元软件中，根据实际构件几何尺寸的特点，可将构件划分为1D单元、2D单元、3D单元。通常，构件的连接位置使用1D单元，如用于模拟焊接和螺栓连接。当构件的厚度方向尺寸远小于另外两个方向尺寸时，可以采用2D单元来模拟，如汽车车身、管路、油箱等薄壁类零件。

该电池包主要为挤压铝型材和钣金件，厚度较薄，在保证计算精度的前提下，为了缩短计算时间，提高计算机工作效率，在有限元模型中将电池包视为一定厚度的片体，将其划分为2D单元[13]。

考虑到电池包建模时间、内部结构的复杂程度及计算量等因素，对其进行简化，将每组电池视为一个质量点，运用集中质量单元[14]通过1D单元与螺栓孔相连接[15]，如图2所示。

图2 电池包有限元模型

电池包的底板及吊耳与横梁、纵梁间的连接采用weld焊接单元[16]。箱盖与横梁、纵梁间的连接采用bolt螺栓单元[17]。根据实际装配过程中的连接位置和连接方式，设置连接单元，保证所建立的电池包有限元仿真模型接近真实情况[18]。

1.2 材料参数

电池包的6061铝合金材料具有抗腐蚀性良好、韧性高、加工后不变形、材料致密无缺陷等特点[19]，在保证结构有足够强度和安全性能的前提下，减少了电池包的质量[20]，其材料参数如表1所示。

表1 材料参数

1.3 边界条件

电池包工作状态下约束模态[21-22]的边界条件为：根据电池包在车上的实际安装情况，约束吊耳螺栓孔处结点的全部自由度[23]。

2 模态分析

运用兰索斯(Lanczos)[24-25]方法对施加约束的有限元模型进行模态分析，提取特征值，得到其固有频率及模态振型。兰索斯方法具有效率高、占用内存少的优势，目前被认为是求解大型矩阵特征值问题的最有效方法，常用在有限元分析中。提取的动力电池包前6阶模态，其固有频率及振型描述如表2所示，各阶振型图如图3所示(图中数字为相应频率下电池包的相对位移)。

表2 固有频率及振型描述

图3 电池包模态振型

由表2可以看出：电池包的前3阶固有频率分别为9.976、18.836、22.223 Hz。传动系统、车身、车桥的振动频率主要集中在0～30 Hz，因此，电池包可能会因受到激励而产生共振，故应采取措施，使其固有频率避开常见的激励频率。

由图3可以看出：振动变形主要出现在电池包箱盖的顶部，原因可能是箱盖为厚度很小的钣金件，刚度较小。因此，可在箱盖上布置加强肋，增加箱盖的局部刚度，以提高固有频率[26]。

3 电池包箱盖的形貌优化

将电池包箱盖顶部设置为布置加强肋的设计区，其余部分为非设计区。选择固有频率最大为优化目标函数，以提高结构刚度。加强肋的最小肋宽设为50 mm，起肋角度为60°，最大起肋高度为20 mm，并且设定肋的分布相对于结构x方向、y方向对称。

采用OptiStruct软件对电池包进行形貌优化。OptiStruct是用于结构分析和优化的设计软件，以有限元方法作为数值计算方法，并带有强大的优化算法，目前广泛用于概念设计和细化设计中。经过软件的迭代优化，得到形貌优化结果如图4所示(图中数字为优化过程中箱盖的变形量，单位为mm)。结合电池包箱盖的制造工艺，对优化结果进行修整，并进行重新建模，得到优化后的箱盖模型如图5所示。优化前的箱盖质量为4.216 7 kg，优化后的箱盖质量为4.226 1 kg，质量增加十分微小。

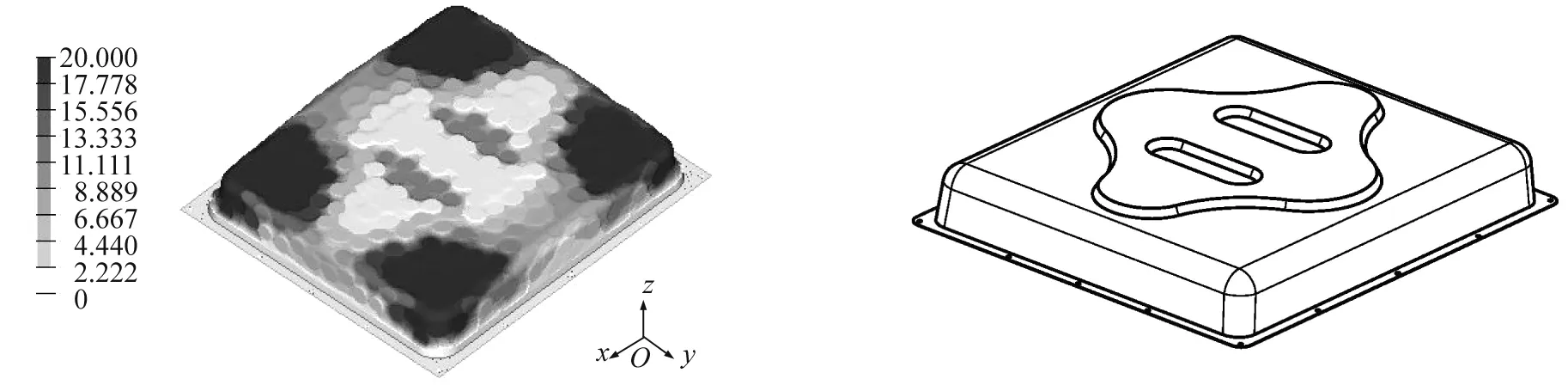
图4 形貌优化结果 图5 优化后的箱盖模型

4 形貌优化前后模态对比分析

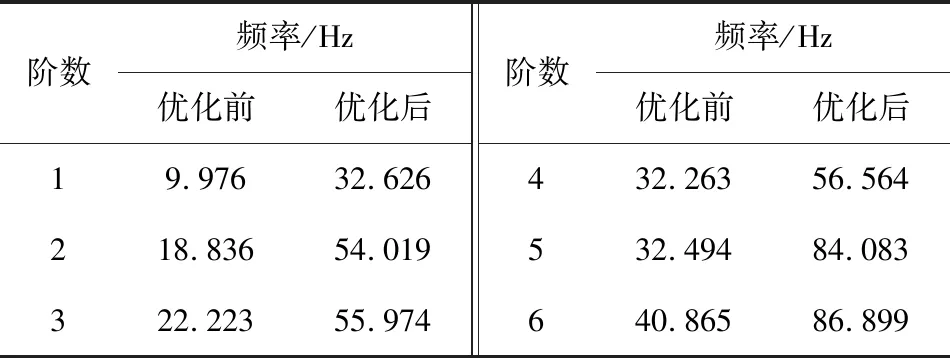
表3 优化前后电池包固有频率对比

使用优化后的箱盖替换电池包上原有箱盖，建立电池包的有限元模型，再次进行模态分析。将优化前后的固有频率进行对比，结果如表3所示。优化后的电池包振型如图6所示(图中数字为相应频率下电池包的相对位移)。

由表3可知：优化后的电池包各阶频率均有提高，且效果显著，一阶频率由9.976 Hz升高至32.626 Hz。优化后电池包的固有频率均大于30 Hz，高于常见的外界激励频率。

由图6可知：优化后电池包的1阶、5阶模态振型的相对位移较优化前稍有增大，因该相对位移并非真实的位移，所以通过振型图无法直接比较优化前后的振动位移，但优化后的固有频率避开了常见激励频率范围，仍可预测其振动情况得到改善。对于优化效果的具体分析，后续还要进行随机振动分析，以得到位移、应力等响应结果。

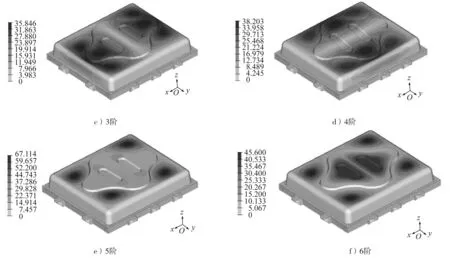
图6 优化后的电池包模态振型

5 结论

1)通过对电池包进行模态分析，得出了电池包的前6阶固有频率及振型，由于电池包箱盖刚度较弱，频率较低时，电池包的振动集中出现在箱盖的顶部。

2)对电池包箱盖进行形貌优化，在箱盖顶部添加加强肋，提高了箱盖刚度。对比优化前后电池包的固有频率，证明了优化后的电池包固有频率得到提高，可避开常见的外界激励频率范围。