机器人轨迹规划控制策略研究

张 霞，孙 强，蔡顺燕，刘 张

(1.成都师范学院 物理与工程技术学院,成都 611130；2.中国科学院沈阳自动化研究所,沈阳 110016 )

0 引 言

轨迹规划是指机器人在作业空间内高效、快速、平稳的完成既定任务，即有效实现末端执行部件的位姿变化和调整，在空域、时域上路径、速度及加速度的规划。基于轨迹规划线性函数，规划机器人在运动学和动力学约束条件下平稳、光滑运动轨迹，对实现机器人高精度、平稳、高效和低功耗作业具有重要意义[1]。目前已有部分学者对上述问题获得一系列的研究成果，针对完成“任务”形式多样性，涌现出示教-再现运动、关节空间运动及空间直线曲线运动等许多轨迹规划及其优化的方法。为了满足工业机器人高效、快速响应要求，时间最优轨迹规划成为热门轨迹优化问题并展开大量研究[2-3]。实际上，能量消耗、振动、脉动的累积等也是机器人轨迹规划的重要性能指标。在文献[4]中，将激振力作为性能指标，利用B样条曲线在运动学和动力学约束条件下进行轨迹优化。丛明，徐晓飞等以时间-脉动最优为目标，同时考虑了运动学约束，利用三次样条函数进行轨迹规划获得了比较平滑的轨迹[5]。利用能量消耗最优轨迹规划算法产生的光滑轨迹更容易进行跟踪且能够减小执行器和机器人结构的应力，并且在一些能源有限的场合，可以节约能源[6]。

考虑动作时间和能量消耗最优的路径规划，通常通过位移、时间样条函数或者三次、五次多项式函数解算光滑轨迹，并在优化过程中考虑速度，加速度，脉动，力矩等约束条件。文献[7]中利用多目标函数法(功效系数法)，采用直线法、折现法和指数法评价动作时间和能量消耗最优解，基于机器人运动学和动力学仿真模型，利用三次多项式函数生成光滑轨迹并逐步迭代优化。文献[8]同样利用三次多项式函数插值规划轨迹，因轨迹不够平滑产生脉动，不连续性脉动造成空间内多关节点加速度陡然增大、轨迹跟踪误差增大并引起关节高频振动，脉动优化成为平稳完成“任务”的研究重点[9]。为了满足机器人空间内作业效率最优、平稳性高的特性，文献[10]提出通过逆运动学解算出与机器人多关节空间位置序列，采用7次B样条函数插值构造各个关节初始、终止时的运动参数，机器人在完成启动和停止运动时其参数可控制，并且运动函数指标(速度、加速度和脉动)均连续的关节轨迹，但其优化目标只包括运动总时间。

本文采用C4连续的5次均匀B样条曲线插值关节位置序列，获得轨迹脉动连续、关节运动参数(速度、加速度)可控的轨迹曲线。为了解决轨迹规划函数中存在的非线性约束问题，并且能够获得全局与局部最优解，本文采用自适应混合遗传算法(Adaptive Hybrid Genetic Algorithm，AHGA)，综合考虑动作时间和能量消耗，在运动学和动力学约束下规划出时间与能量综合最优且脉动连续的轨迹。

1 空间轨迹优化

考虑机器人运动过程需保持较高稳定性，该文所述机器人本体采用同步带传动方案。该机构形式存在刚性不足特点，在较大速度和加速度工作时产生振动，造成空间关节速度、加速度的突变[5]。基于上述情况，本文运用逆运动学方程将已规划路径转化为关节空间节点，基于五次B样条函数构造轨迹，实现空间节点平滑的连接，根据实际需求优化并提高运动快速性和功耗。由于空间关节运动时间一致，轨迹规划流程图如图1所示。

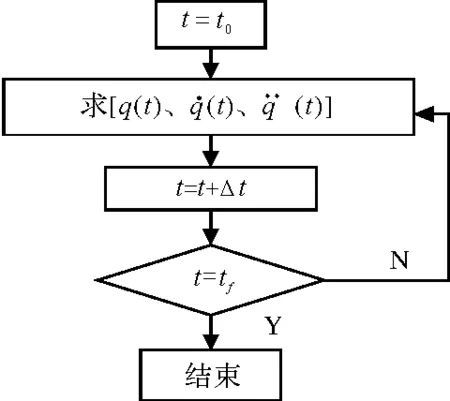
图1 轨迹规划流程图

图中，Δt为伺服控制采样周期。

五次B样条曲线方程为

(1)

式中，di+j-1为控制点，i=1,2,…,n-1，u∈(0,1)，Qi(u)为第i段B样条曲线上的关节结点，Nj,5(u)为5次规范B样条基函数。

写成矩阵形式：

(2)

di-1,di,di+1,di+1,di+3,di+4为组控制点；Qi(u)为曲线上的点，u为参数，0≤u≤1，其上点的横、纵坐标分别用t(u)、q(u)表示.

B样条轨迹曲线Qi(u)(其中i=1,2,…,n-1)对时间t进行三阶求导，获得机构本体的轨迹速度、加速度和脉动，函数如下：

(3)

已构造五次均匀B样条轨迹并不是最优运动轨迹，在实际应用中，需要对其进行优化，使轨迹更光滑。以时间最短和能耗最小为优化目标，采用改进优化的线性加权法进行轨迹优化，函数如下：

综合考虑时间和能量对轨迹的影响，采用线性加权法对已构造样条轨迹进行优化，定义目标函数如下：

(4)

机器人关节速度、加速度、脉动和力矩极限值分别为vcj、acj、jcj和Tcj，作为约束条件对机器人运动学和动力学指标进行优化。

(1)关节速度值

(5)

j=1,2,3，i=1,2,…,n-1

(2)关节加速度值

(6)

j=1,2,3，i=1,2,…,n-1

(3)关节脉动值

(7)

j=1,2,3,i=1,2,…,n-1

(4)关节力或者力矩

(8)

j=1,2,3,i=1,2,…,n-1

2 自适应混合遗传算法

遗传算法计算是基于自然界生物适者生存的规律提出的一种随机优化算法。计算过程简单、高效，但在使用过程中提前收敛、无法获取局部最优解缺陷[6]。

优化方法主要有微粒群算法(PSO)、差分进化算法(DE)、基于假设检验的模拟退火算法(SA)等[7]，上述方法局部搜索能力优，但考虑无法获取局部最优解缺陷，将局部搜索能力优的算法与遗传算法相结合，提出一种混合遗传算法，达到搜索能力提高的目的[8]。

该混合遗传算法从随机生成的初始群体出发，有效空间中搜索全局最优解，算法流程如图2所示。

图2 算法流程图

3 仿真结果

仿真验证算法参数为如下：群体规模M取50，迭代次数为200，转化系数α=1，Pc1=0.9，Pc2=0.6，Pm1=0.1,Pm2=0.001。机器人完成既定路径规划并且各关节可无碰撞平稳运行，利用空间坐标系变换得到的逆运动学方程求解机器人各个关节的位置序列，如表1所示。根据第2节已确定边界约束参数和选型的电机额定扭矩，计算出机构本体动力学参数，如表2所示。

表1 机器人关节位置序列

表2 机器人约束

表3 SGA最优轨迹规划结果

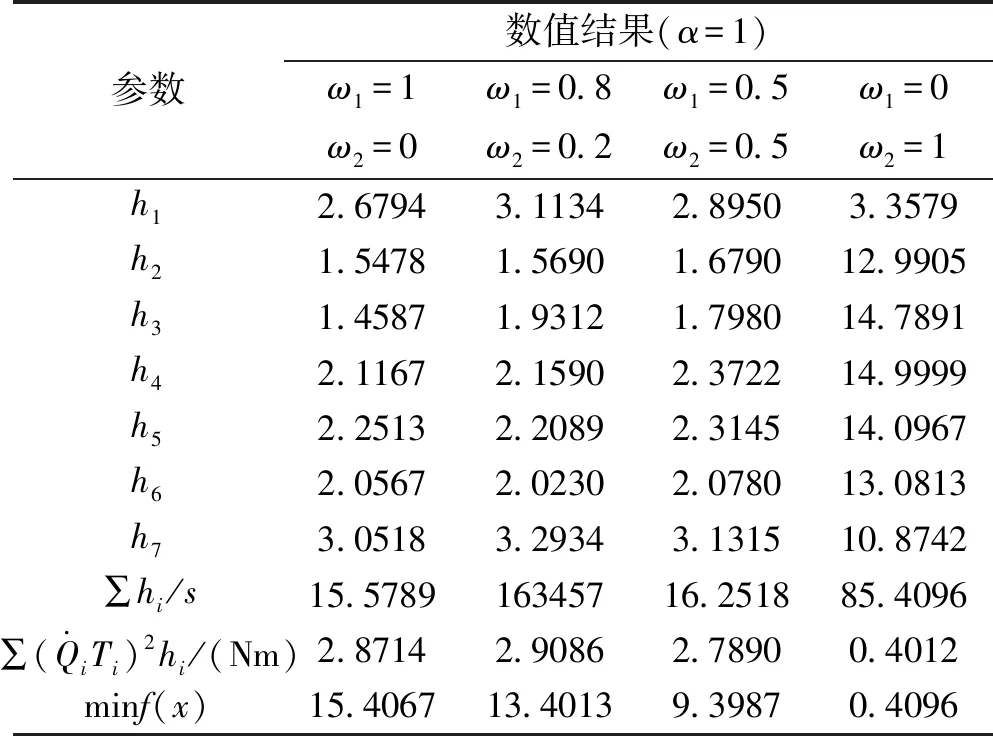
表4 AHGA最优轨迹规划结果

经过对表3和表4的对比可知，所述优化后的混合遗传算法同自适应遗传算法比较，局部搜索收敛能力更强。利用AHGA方法进行轨迹优化，在ω1=ω2=0.5情况下获得三个关节的位置p、速度v、加速度a、脉动j的优化解如图3～5所示。图中，位置为p，速度为v，加速度为a，脉动j。

图3所示，仿真曲线表明在0～18s时域完成既定运动轨迹，机器人3个关节在起始、末端速度和加速度均为零，纵坐标所示关节速度、加速度与脉动参数曲线连续、平滑，机器人各关节轨迹跟踪的误差效果最优。

图3 优化轨迹

4 试验验证

以硅片传输机器人为试验平台，基于虚拟样机验证轨迹规划策略和遗传优化算法有效性。机器人具有三个自由度，1轴伸缩，2轴的回转与3轴的升降，具体结构如图4所示。

图4 ADAMS仿真模型

对采用五次B样条和三次B样条规划的关节轨迹性能进行试验对比研究。在关节伺服控制器结构参数不变的情况下，将最优平滑轨迹按照机器人关节伺服控制周期离散化，送入伺服控制器做轨迹跟踪控制实验，关节伺服控制周期为1.28 ms。

4.1 机器人系统搭建

机器人系统主要包括机器人本体、控制系统、电源模块和软件模块组成。

机器人运动控制系统采用主从式结构，包括上位机和下位机。上位机完成机器人运动轨迹参数设定、上电初始化和运动参数实时反馈。下位机进行控制，包括硬件层面的PLC控制、软件层面的轨迹规划以及数据采集等功能，控制系统原理如图5所示。

图5 控制系统原理

机器人控制系统采用位置环闭环控制，编码器实现位置信息反馈，通过调整微分、积分、比例环节等参数，使其满足运动性能。

4.2 软件实现

控制系统软件主要是上位机软件的设计，本文软件采用VC++编写，并调用PMAC运动控制卡带有的运动控制库函数实现机器人的运动控制，本文软件具有离线优化和在线控制的功能。

软件的离线功能主要是用于机器人轨迹的优化计算，在线功能是用于实时生成运动轨迹实现机器人运动控制。

人机交互界面如图6所示，输入区为轨迹优化算法设计变量，型值点表示机器人3个关节运动路径的结点，显示区实时显示机构本体3个轴的位置与速度参数，运动程序可以完成三次和五次B样条两种轨迹规划的运动。

图6 人机界面

5 实验验证

机构本体控制流程图如图7所示，根据接收的3个关节空间坐标信息转换成机器人的运动轨迹，根据伺服周期将轨迹划分为很多段运动控制信息，并发送至下位机PMAC卡中，PMAC板将信号流发送到各关节驱动实现马达按照既定要求运动，各个关节采用闭环控制，传动链末端通过编码器完成位置信息反馈。

图7 系统控制策略

仿真与实物样机实验对比，三个关节的位置和角速度曲线如图8～10所示，表明自适应混合遗传算法优化的轨迹平滑性较好，具有较好的轨迹跟踪能力。

图8 1轴位置和角速度曲线

图9 2轴位置和角速度曲线

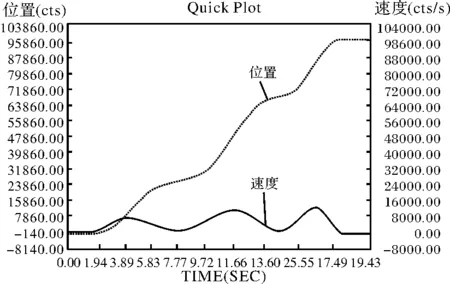
图10 3轴位置和角速度曲线

保证其它参数一致，验证不同插值函数计算得到的轨迹性能，本文采集轨迹跟踪误差并利用Matlab处理数据，3个关节轴位置跟踪误差绝对值曲线，如图11所示。

error1-三次B样条跟踪误差，error2-五次B样条跟踪误差

通过对各个关节轨迹的观察发现，最优解可满足既定约束参数；各关节始末速度、加速度为零，且关节速度、加速度与脉动曲线均连续、平滑，机器人关节轨迹跟踪误差降低到最小程度。

3个关节五次B样条轨迹所示的位置跟踪最大误差分别为 ；误差均方根分别为 ；3个关节的三次B样条轨迹位置跟踪最大误差分别为 ；误差均方根分别为 。试验表明轨迹规划方法具备可有效降低轨迹跟踪误差优点。

6 结 语

本文根据机器人工作特点，在考虑机器人运动学约束条件的同时，对机器人的运动轨迹进行优化，并提出一种关节空间中机器人时间与能量综合最优轨迹规划方法；针对机器人关节运动轨迹非线性约束全局与局部最优解要求，提出一种优化的自适应混合遗传算法，利用阀函数处理非线性约束问题。同时融合随机方向搜索的方法，提高了局部搜索能力和解的质。仿真计算和试验表明本文数值优化算法可获得性能良好运动轨迹解算，所述轨迹规划方法可达到提高机器人轨迹跟踪精度的优点。