OFDM/OQAM技术在时频弥散信道中的应用

戴 晖，姜晓斐，杨万君

(1.装备发展部信息系统局，北京 100034；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；3.陆军北京军代局驻石家庄地区军代室，河北 石家庄 050081)

0 引言

随着社会的进步与发展，高速移动载体将成为未来的主要出行方式。而在高速移动中，无线信道的时变性更强，往往具有多普勒频移大、时频弥散的特点，即信道呈现时频弥散特性。传统的OFDM等传输技术带外辐射较大，对符号定时和载波频率偏移十分敏感，其在时频弥散信道上应用存在一定问题。为了对抗时频弥散信道，即时间—频率双选衰落信道的影响，通过选取具有良好时频聚焦特性的成形滤波器函数用于OFDM系统，是一种能有效提高OFDM系统性能和信道资源利用率的技术路线。基于此思想，一些学者提出了基于交错正交调制的OFDM/OQAM。

OFDM/OQAM技术可通过各种不同的数字滤波器对信号频谱进行成形滤波，使得它们的带外辐射远低于OFDM，具有良好的抗符号间干扰(ISI)和子载波间干扰(ICI)的能力，且不需要循环前缀(CP)作为保护。相对于OFDM/CP系统来说，OFDM/OQAM系统具有以下3个优点：

① 由于OFDM/OQAM系统的脉冲函数具有较好的时频聚焦特性(Time Frequency Localization，TFL)，在信道的冲击响应长度是OFDM/OQAM符号长度的10%以内时，可以不加CP，从而提高系统的有效性；

② 时频聚焦特性较好的脉冲成形函数增强了OFDM/OQAM系统抗多普勒频移和抗多径能力，因此可以进一步增大OFDM系统的应用场景；

③ OFDM/OQAM系统中，由于需要保证实数正交，所以在发射端将星座图映射后的信息分成2部分发射出去，由于是实数，所以载荷信息量只有经典OFDM的传输效率的一半，但是由于数据量是经典OFDM的2倍，所以整体的传输效率与经典OFDM传输效率一致，但是由于不加CP，所以传输效率比OFDM/CP要高。

本文给出OFDM/OQAM系统的数学模型，并对比分析OFDM/OQAM系统与CP-OFDM在不同阶数调制下的性能，进一步指出在时频弥散信道中OFDM/OQAM系统关键技术的现有成果及其发展趋势。

1 研究现状

Rurton R.Saltzberg在1967年提出了OFDM/OQAM系统的数学模型[1]，奠定了OFDM/OQAM系统的理论基础。Botaro Hirosaki在1980年提出了OFDM/OQAM系统的数字化方法，这样就完成了OFDM/OQAM系统的数字化过程。现阶段在国外，无论是OFDM/OQAM技术的理论研究还是应用研究，都取得了非常大的成就[2-5]。研究者们重点对成型脉冲滤波器函数的选取以及OFDM/OQAM系统的实现形式进行了更深入研究。除此之外，研究者们还提出了基于循环前缀的OFDM/OQAM系统[6-7]和基于共轭对称矩阵的改进型OFDM/OQAM系统[8]。在系统应用方面，有文章讨论了OFDM/OQAM系统和CP-OFDM系统的性能差异[9-10]。还有文章研究了OFDM/OQAM系统在认知无线电[11]、数字陆地电视广播系统[12]、无限区域局域网[13]以及电力线通信等多个领域中的应用[14]。

在国内，早期对OFDM/OQAM系统的研究成果相对于国外来说少一些。但2000年之后，国内研究者对OFDM/OQAM技术产生了浓厚的兴趣，也有了一部分研究成果。其中电子科技大学[15-17]、浙江大学的研究团队[18]在OFDM/OQAM系统关键技术的研究成果比较突出，主要集中在信道估计与均衡、同步技术等方面。

2 OFDM/OQAM系统模型

OFDM/OQAM与经典的OFDM最大的不同点就是脉冲成型函数不一样，由于前者采用的脉冲成型函数不能够保证在复数域内正交，而在实数域内能够保持正交，因此经典的OFDM中的QAM映射变成了OQAM的映射方式。基于此，Sioha提出了OFDM/OQAM系统结构，如图1所示。

图1 OFDM/OQAM系统结构

图1中，g(t)为发送端脉冲成形滤波器；g*(t)为接收端的匹配滤波器。首先每个数据经过数据交错就是将复数分成实数和虚数2部分，然后进行N/2倍的上采样，采样之后的数据经过脉冲成型滤波器，和其他数据进行叠加，然后发射出去。从整体上看，由于上采样是N/2，在所有数据相加发射出去之后，使得符号的整体持续时间没有变；而OFDM/OQAM虽然可发送的数据量是原来的2倍，但由于每个数据载荷的信息是OFDM/QAM的一半，所以二者的传输效率一样(这里表示每个OFDM/OQAM符号的传输效率与CP-OFDM是一致的，但由于CP-OFDM需要添加循环前缀CP，因此其系统整体传输效率低于OFDM/OQAM系统)。

首先，接收端的数学模型为：

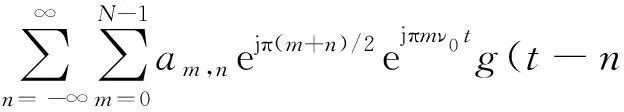
(1)

其中，am,n(n∈Z,m=0,1,...N-1)表示在数据处于时频格点的第n个符号内的第m个子载波上，其实这里是类比于OFDM/OQAM；τ0和υ0分别表示OFDM/OQAM时频网格中数据的时域持续时间和频域持续时间，且τ0υ0=1/2；前面已经介绍了，OFDM/OQAM系统是正交的，那么它的正交性是如何体现的呢，接收端如保证解调效果呢，为了便于分析和解释OFDM/OQAM接收解调原理，分析基函数gm,n(t)的正交性，则：

(2)

令t-nτ0=x+(k-n)τ0/2，则式(2)可以重写为：

(3)

其中，Ag(τ,υ)是模糊函数，其定义为：

(4)

模糊函数通常应用于雷达上面，它是一种分析时频二维域的有效工具，在这里借鉴过来，是来自对TFL的讨论，简单理解OFDM/OQAM中的模糊函数就是在时间和频率上的相关程度。通过分析式(4)的正交条件，则不难看出成形滤波函数g(t)必须是偶函数，如果单纯的讨论相位因子，则可将式(4)改写为

(5)

考虑到n+k+1=(n-k)+(2k+1)，n-k与n+k-1满足互异性，即如果n-k是偶数(奇数)，则n+k-1为奇数(偶数)，所以，综合式(4)与式(5)，实正交条件可重新表示为：

(6)

由τ0ν0=1/2可知，当成形滤波函数g(t)满足下式即可实现实正交条件：

(7)

则重写正交性表达式，可得：

(8)

在此需要说明的是，系统解调后接收端如果不取实数的情况下，得到的是一个复数值，其中的实数是所需要的，而虚部那一部分则是要丢弃的，而OFDM/OQAM实正交也是来源于此。

为了验证OFDM/OQAM系统性能，在AWGN信道下，对OFDM/OQAM系统进行仿真，OFDM/OQAM，OFDM在高白信道下的仿真结果如图2所示，系统建立的是基带的信息模型。从图2中可以看出，OFDM/OQAM与OFDM的仿真结果与QAM的理论值相当，从而验证了基于IFFT/FFT的OFDM/OQAM快速实现方案的正确性。特别说明的是，OQAM与QAM的BER理论值上是相等的，所以在此就没有再绘出OQPSK的理论BER曲线。

图2 OFDM/OQAM高白信道下仿真

然而在采用高阶调制时OFDM/OQAM系统的性能较差，仿真结果如图3所示。可以看出，即使在高斯白噪声信道下，系统的误码率性能依然很不理想。通过查阅文献，发现OFDM/OQAM系统在高阶调制方式下不是一个可以完美重建的系统模型，参考文献[19-21]中对此问题进行了详细阐述。即由于高阶调制引入了严重的系统自扰导致系统性能平台，由图中的曲线可以看出，在较低信噪比时，误码率曲线随噪声的减小降低，随着信噪比的增强，固有的自干扰成为影响系统性能的主要因素，系统进入误码率平台。通过该仿真进一步验证了由于系统本身的特性决定了在OFDM/OQAM系统中无法使用高阶调制技术，因此目前的研究都是在OQPSK调制方式下进行的。

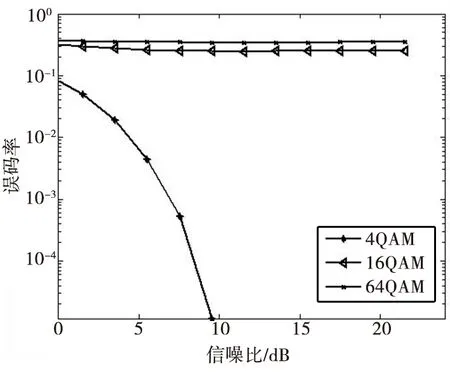
(a)4进制、16进制与64进制对比

(b)局部放大图图3 高斯白噪声信道下不同调制方式的误码率仿真

3 OFDM/OQAM系统关键技术

由系统模型分析可知，OFDM/OQAM系统无需添加循环前缀，通过采用具有良好时频聚焦特性的脉冲成型函数，从而有效提升系统的抗多径和抗多普勒能力、传输效率等指标。但同时也带来了如下问题：

① 脉冲成型函数的选取直接关系到系统的性能，但同时具备良好时频聚焦特性的脉冲成型函数设计难度较大；

② 系统的固有干扰(仅满足实正交特性，虚部干扰难以避免)使得系统接收端算法处理更加复杂，且难以直接应用传统CP-OFDM的已有研究成果。

基于以上分析，并结合当前国内外研究现状，OFDM/OQAM技术未来的研究热点将主要集中在以下3个方面。

3.1 良好时频聚集特性的脉冲成型函数设计

OFDM/OQAM所引入的具有良好时频聚焦性的脉冲成型波形可改善OFDM系统的子载波频谱结构，调整子载波正交条件及时频格点间距等。同时，依赖脉冲成型函数良好的时频聚焦特性，可以不使用传统的CP结构，提高频谱效率。因此，脉冲成型函数设计是OFDM/OQAM区别于传统OFDM系统的基础，也是其研究的热点问题。

OFDM/OQAM目前常用的脉冲成型波形是扩展高斯函数(Extended Gussian Function，EGF)，使系统在无循环前缀(Cyclic Prefix，CP)的条件下兼具良好的抗ISI和ICI能力。

同时，EGF函数可通过调整其扩展因子α使其具备时频可调特性，经分析有如下结论：

①α<1，EGF函数随着时间偏移缓慢下降，因此该条件下EGF函数具有很好的时间聚焦特性，且能够有效抑制ISI；

②α=1，EGF函数就是IOTA函数，时频域具有相同的扩展特性，抑制ICI和ISI的性能也相同；

③α>1，EGF函数随着频率偏移缓慢下降，因此该条件下EGF函数具有很好的频率聚焦特性，且能够有效抑制ICI。

目前，对脉冲成型函数的设计主要包括两方面：一方面是研究新型的具有良好时频聚焦特性的成型函数；另一方面则是以EGF函数为基础，结合信道特性通过优化信干噪比(Signal to Interference Noise Ratio，SINR)获取最优化滤波器参数。

3.2 抗虚部干扰的导频设计与信道估计

信道估计是时频双选择性衰落信道适应的基础，而导频设计与信道估计密不可分。目前最为成熟的信道估计是基于数据辅助型的，在OFDM系统中，还要根据信道类型来设计不同的导频形式，以对抗不同类型的衰落信道。而在OFDM/OQAM系统中，由于引入了脉冲成型函数进行滤波处理，不可避免地在实正交之外会产生虚部干扰，这就造成了OFDM/OQAM系统的导频设计结构与OFDM/CP有着不一样的特点。

相比于OFDM系统，OFDM/OQAM系统中存在固有的虚数干扰问题，这是OFDM/OQAM系统的一个特殊性，在信道估计算法研究中必须加以考虑。因而传统的应用于CP-OFDM系统中的信道估计算法将不再适用。OFDM/OQAM系统的固有干扰问题如图4所示。

图4 OFDM/OQAM系统固有干扰分布

从图4中可以看出，导频数据周围的所有发送数据符号均对导频数据产生了干扰，即系统的固有干扰。OFDM/OQAM系统的导频设计与信道估计则针对系统这一固有干扰进行改进；目前主要有2种方式：基于干扰消除的方式和基于等效功率最大的方式。但这2种方式设计得到的导频均属于块状导频，因此对于快速时变信道来说，其实用性不强。

3.3 信道均衡技术

多载波系统与单载波系统相比，一个重大的优势就是其均衡可以采用简单的频域均衡。在OFDM/CP系统中，由于采用CP将数字域离散的圆周卷积与线性卷积进行等效，使得均衡变得尤为简单。但是在OFDM/OQAM系统中，由于不加入CP，仅仅依靠脉冲函数良好的TFL性能来抑制信道的多径效应，因此不能够完全消除信道给系统带来的ISI。信道的弥散性会使得OFDM/OQAM系统产生虚部干扰，这使得OFDM/OQAM系统的均衡较于OFDM/CP变得复杂。

为了提升OFDM/OQAM系统均衡的效率，多结合信道估计采用干扰消除的方式。然而干扰消除的准确性，是建立在周围信号点的准确性、信道估计准确等基础上的。但是在快速时变信道中，这些条件很难同时满足，从而也造成了基于干扰消除算法的粗糙性。尤其对于虚部干扰比较敏感的情况下，比如在高阶调制和高动态情况下，系统在虚部干扰情况下回很快进入性能平台，从而降低系统的有效性。

为此，当前较为有效的方式是基于迭代的干扰消除算法。然而随着迭代次数的增加，算法性能增加趋于饱和。同时基于干扰消除法的计算量过于复杂，这是基于干扰消除方法的一个重大缺陷。

4 结束语

OFDM/OQAM系统由于其正交性条件放宽(仅实部正交)引入的虚部干扰，为系统的实现带来了巨大的挑战，包括：采用高阶调制时存在系统性能的地板效应；脉冲成型设计需满足实正交特征，可设计参数较少，且设计与系统的应用环境关联性强，增加系统的设计复杂度；系统固有的虚部干扰大幅增加了导频设计的难度，信道估计与均衡算法也将更加复杂。可以看到，目前OFDM/OQAM系统在相关关键技术方面已经有了较多技术积累，可通过进一步的深入研究，发挥其相对于传统CP-OFDM系统更高的时频资源有效利用、更强的信道适应性等特点，在无线通信中特别是在时频弥散信道中具有较为广阔的应用前景。