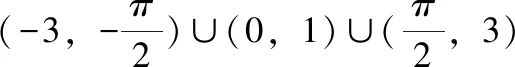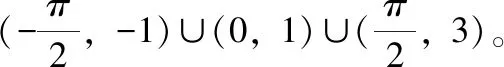有效把握题目信息，破解审题关

文丰顺县华侨中学

学数学离不开解题，解题离不开审题，审题是解题的钥匙。著名数学教育家波利亚说：“最糟糕的情况是学生没有弄清问题就进行演算和作图。”在解题时，学生往往不能把握有效信息来破解审题关，导致出错或费时而无所得。本文从有效把握信息的角度尝试提出破解审题关的路径。

一、把握结论与条件的联系信息，破解审题关

结论是解题的终极目标，根据分析法和综合法，解决问题的思维很多情形下都是在目标意识和条件间的联系下双向驱动的。把握结论要探索已知条件和结论间的联系与转化规律，善于从结论中捕捉解题有效信息，确定解题方向。

通过观察发现条件(1)式和(2)分别是正弦和余弦的两角和，而要求的是两角的余弦差，我们把握cos(α-β)=cosαcosβ+sinαsinβ这一公式特征，把cosαcosβ和sinαsinβ看成整体，那么条件(1)和(2)中，如果能找到cosαcosβ和sinαsinβ就能解决了，联系到同角基本关系式有平方关系，若把(1)和(2)同时平方再相加就迎刃而解了。

二、把握题目条件信息，破解审题关

题目所给出的条件信息是解题的根，要充分利用题目的条件的内在信息。审清条件信息的关键要素，充分挖掘隐含的条件信息，破解审题关。

例1.过点A(1，-1)、B(-1，1)且圆心在直线x+y-2=0上的圆的方程是( )

A.(x-3)2+(y+1)2=4

B.(x+3)2+(y-1)2=4

C.(x-1)2+(y-1)2=4

D.(x+1)2+(y+1)2=4

若利用选择题的特殊性——答案在选项中，充分使用好条件的凸显信息，可检验四个选择支是否满足条件：首先选项(B)、(D)的圆心不在直线x+y-2=0上，其次选项(A)的圆不过点A(1，-1)。

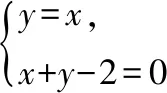
三、把握条件的结构信息，破解审题关

式子的结构特征是数学问题的体现形式，某些问题在已知的结构形式中常常隐含着某种内在的结构关系信息，把握结构信息就要求对结构进行分析、变形、拆分和转化，以破解审题关。

例3.设{an}是首项为1的正项数列，且(n+1)an+12-nan2+an+1an=0 (n=1，2，3…)，则它的通项公式是an=。

四、把握题目的数值信息，破解审题关

数值是数学运算中最常见的要素，式子的数值关系往往能暗示解题的方向。把握数值有效信息要善于观察规律、分析数值关联，从数值本身的变化规律，数字与数字之间的联系去寻找解题的思路，获得便捷的解法。

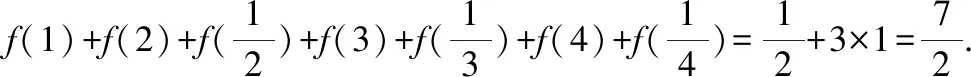
五、把握题目的图形信息，破解审题关

图形是数学问题的几何表现形式。把握图形信息就要把握图形的本质特征，或赋予问题中的某些代数关系以图形意义，利用图像做出透彻分析，从而找到解题途径。

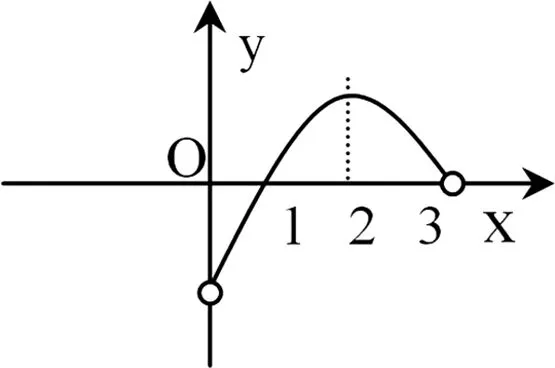
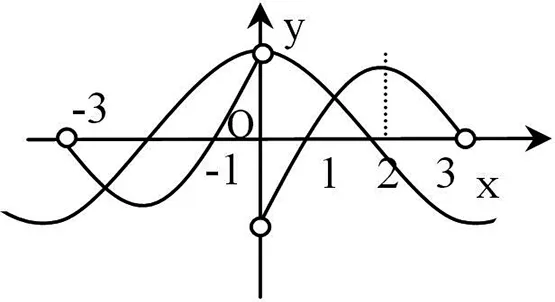
例5.已知f(x)是定义在(-3，3)上的奇函数，当0

图1

C.(-3，-1)∪(0，1)∪(1，3)

图2