基于CEL方法的压差驱动式管道机器人动力特性分析

江旭东 ，孙其海，滕晓艳

(1. 哈尔滨理工大学 机械动力工程学院，哈尔滨 150080； 2. 哈尔滨工程大学 机电工程学院，哈尔滨 150001)

压差驱动式管道机器人依靠首尾两端流体介质的压力差实现自驱动，尤其适合长距离在役油气管线的检测作业。压差驱动式管道机器人在作业过程中，运行速度平稳性和环境适应性(弯管通过性以及越障能力)将直接影响其作业质量。管道机器人运动过程涉及各舱段的刚体运动，也伴随密封皮碗的超弹性大变形和结构系统与管内流体的流固耦合作用，属于典型的柔性多体流固耦合动力学问题。Lesani等[1]，Liang等[2]将管道机器人简化为集中质量系统，分析了管道机器人的运动性能和制动特性；Mirshamsi等[3]考虑了质量分布特性对于管道机器人动力特性的影响。Zhang等[4-5]考虑了密封皮碗与焊缝的接触作用，建立了管道机器人的弹簧-阻尼-质量系统，分析了管道机器人的越障能力。Zhu等[6-7]考虑了密封皮碗与管道内壁的过盈接触作用，建立了舱段(刚体)-密封皮碗(超弹性)-管道内壁作用系统的轴对称动力学模型，预测了管道机器人与管道内壁的接触力。

但是，上述分析模型忽略了压差驱动式管道机器人作为多柔体系统与管内流体的耦合作用，难以精确预测管道机器人在复杂管道内的动力特性。耦合的欧拉-拉格朗日方法(Coupled Eulerian-Lagrangian，CEL)，采用基于体积分数的流固耦合边界追踪算法，自动在结构和流体域间进行载荷、位移、速度等信息的传递，能够解决切削加工[8-9]、空化射流冲击[10-11]、大尺度结构[12-13]以及转子系统[14-16]的流固耦合问题。流体压差驱动下的管道机器人的振动响应属于复杂的流固耦合问题。由此，本文基于CEL方法构建压差驱动式管道机器人的柔性多体流固耦合动力学模型，预示管道机器人在复杂管道内的结构动力响应。对比不同管道内径和机器人舱段长度下的密封皮碗应力场、管道与机器人间的摩擦力和流体对管道机器人的驱动压差，分析管道与机器人尺寸参数对机器人结构动力特性的影响。

1 管道机器人流固耦合模型

压差驱动式管道机器人由驱动舱段和作业舱段组成，两者通过双万向联轴节组成(如图1所示)。管道简化为刚体，管道机器人结构系统作为拉格朗日部件，管道流体作为欧拉部件。拉格朗日域划和欧拉域分别采用双向性减缩积分单元C3D8R与EC3D8R(如图2所示)。考虑到管道-机器人-流体间复杂的接触行为，通过基于惩罚函数法的通用接触算法描述多体系统的相互作用，采用基于体积分数的CEL方法模拟管道机器人系统的动力特性。

图1 压差驱动式管道机器人

1.1 流体域控制方程

流体域满足连续性方程和Navier-Stokes方程，则有：

(a) 管道机器人(拉格朗日网格)

(b) 流体(欧拉网格)

(1)

式中：ρf、g为分别流体的密度和体力，vf、σf分别为流体的速度和Cauchy应力张量。

假设管内流体为可压缩牛顿流体，Cauchy应力张量表示为：

(2)

式中：p是流体压强，μf是流体动力黏度，I是二阶单位张量。

基于Shyue[17]，通过Mie-Gruneisen状态方程表示流体压强，则有：

(3)

式中：ρf0、cf0分别为流体初始密度和声速，η为名义体积压缩应变，且η=1-ρf0/ρf，Γ0、s为材料常数，Em为单位质量内能。

1.2 结构域控制方程

通过2参数Mooney-Rivlin模型对聚氨酯橡胶材料描述密封皮碗的超弹性本构关系，则有：

(4)

根据Green方法，不可压缩超弹性材料的本构关系为：

(5)

(6)

式中：σs,u为聚氨酯橡胶材料的单轴应力。

由此，将聚氨酯橡胶材料制成标准试件(如图3所示)，根据式(6)拟合单轴拉伸实验数据(如图4所示)，获得Mooney-Rivlin模型参数：C10=0.191 MPa，C01=1.25 MPa。

Ⅰ型试验样本

Ⅱ型试验样本

图4 聚氨酯单轴拉伸应力-应变关系

1.3 流固耦合界面

在CEL方法中，流体域(欧拉域)以及自由表面通过体积分数跟踪描述[18-19]。体积分数为1代表欧拉单元充满流体，体积分数为0代表欧拉单元内无流体填充(如图5所示)。

由于流体遵循连续性方程，则体积分数F满足如下守恒关系：

(7)

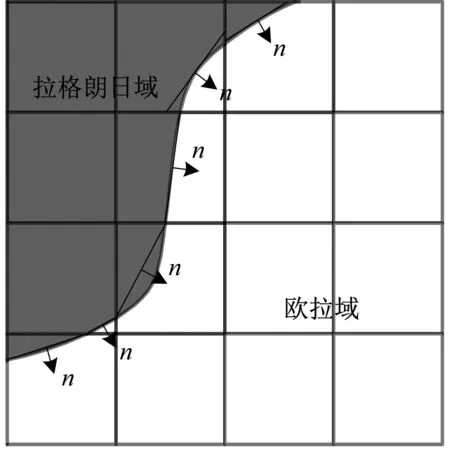
(a) 接触面法线

(b) 重构后接触界面

根据欧拉单元体积分数的当前值，结合拉格朗日域的结构边界的法矢，通过逐段线性逼近的方法确定流固耦合边界。利用流固耦合边界传递欧拉域与拉格朗日域的相互作用，拉格朗日域和欧拉域的接触通过基于罚函数耦合算法的通用接触分析获得(如图6所示)。

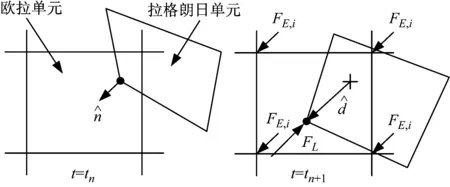
图6 罚函数耦合算法

基于通用接触算法，欧拉单元与拉格朗日单元发生相互倾彻时，产生的接触惩罚力Fp表示为：

(8)

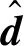
惩罚刚度由欧拉单元与拉格朗日单元的惯性决定，表示为：

(9)

式中：mL是拉格朗日节点处的质量，mE是通过欧拉单元基函数在倾彻点处插值获得的质量，Δt为时间增量步，ε为乘子系数(一般取为4%～5%)。

根据式(8)和(9)，将接触惩罚力向欧拉单元的各个节点等效，则有：

(10)

式中：FE,i、mE,i分别为欧拉单元的节点力和质量，Ni为欧拉单元的基函数。

拉格朗日单元的节点力FL与欧拉单元的节点力平衡，则有：

(11)

1.4 边界条件

设置欧拉域入口为均匀流速，出口为自由边界。管道简化为刚体，约束其所有空间自由度，双万向联轴节的转动副通过具有旋转属性的连接单元描述。在管道内腔、流体域和管道机器人间施加通用接触约束。根据管道机器人结构域相对于流体域的位置，通过布尔运算计算欧拉单元的体积分数，进而确定初始流固耦合界面(如图7所示)。

(a) 初始体积分数

(b) 速度边界

1.5 方程求解

联立式(1)～(11)，通过有限元方法求解CEL方法的流固耦合模型，采用Newmark显式积分算法构造上述控制方程的迭代格式，则有：

(12)

2 结果分析

管道机器人运行于入口速度v=3 m/s的蛇形管道，入口段管道内径D0=324 mm，缩径段管道内径D1=300 mm，管道壁厚t1=8 mm，两段弯道的曲率半径分别为3D1和1.5D1(如图7所示)。管道机器人舱段长度Lc=380 mm，双万向联轴节长度L2=315 mm，密封皮碗外径D2=324 mm，密封皮碗厚度t2=15 mm。通过CEL仿真分析，分别获得了密封皮碗的危险工况和应力场(如图8所示)，管道机器人的行走速度(约定为驱动舱段的运行速度)、驱动压差和摩擦力(如图9所示)。

(a) 3D弯道

(b) 1.5D弯道

作业舱段受到弯道的几何约束和离心力的作用，其密封皮碗在管道内测经历局部化挤压作用产生高应力区域，在3D弯道处形成的最大等效应力为1.936 MPa，在1.5D弯道处产生的最大等效应力为2.316 MPa。

管道机器人由入口段进入缩径段时(t=0～0.12 s)，密封皮碗渐次进入缩径段，摩擦力逐渐上升；同时，在驱动压差作用下管道机器人加速运动，形成峰值速度6.5 m/s；在t=0.12 s时，驱动舱段即将进入3D弯道，引起瞬时峰值摩擦力7 kN和峰值压差0.65 MPa。管道机器人在3D弯道内时(t=0.12～0.32 s)，密封皮碗与管壁的接触作用变弱导致摩擦力下降(如图7(a)所示)，但是驱动压差下降更加显著引起管道机器人减速运动。管道机器人由3D弯道进入直线管道(t=0.32～0.53 s)时，摩擦力波动范围为4.30～4.97 kN，驱动压差波动范围为0.05～0.32 MPa，管道机器人缓慢加速。管道机器人在1.5D弯道内时(t=0.53～0.67 s)，作业舱段的密封皮碗与管壁产生缝隙(如图7(b)所示)，摩擦力下降至谷值2.8 kN。管道机器人由1.5D弯道进入出口段直线管道时(t=0.67～0.8 s)，摩擦力逐渐增加趋于稳定，驱动压差在管道机器人位于直线管道时小幅波动导致机器人速度趋于平稳。

为了比较机器人结构参数和管道几何参数对机器人动力特性的影响，后续分析中将对摩擦力和驱动压差等瞬态响应在时间历程上取平均值，即通过平均摩擦力和平均驱动压差反映机器人的负载特性和自驱动能力。

(a) 速度

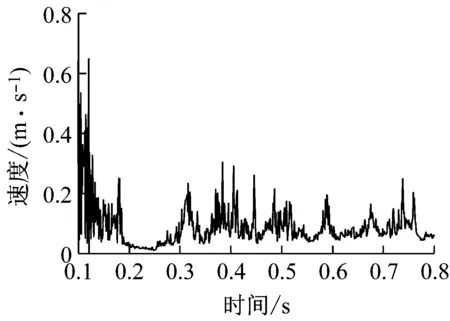
(b) 驱动压差

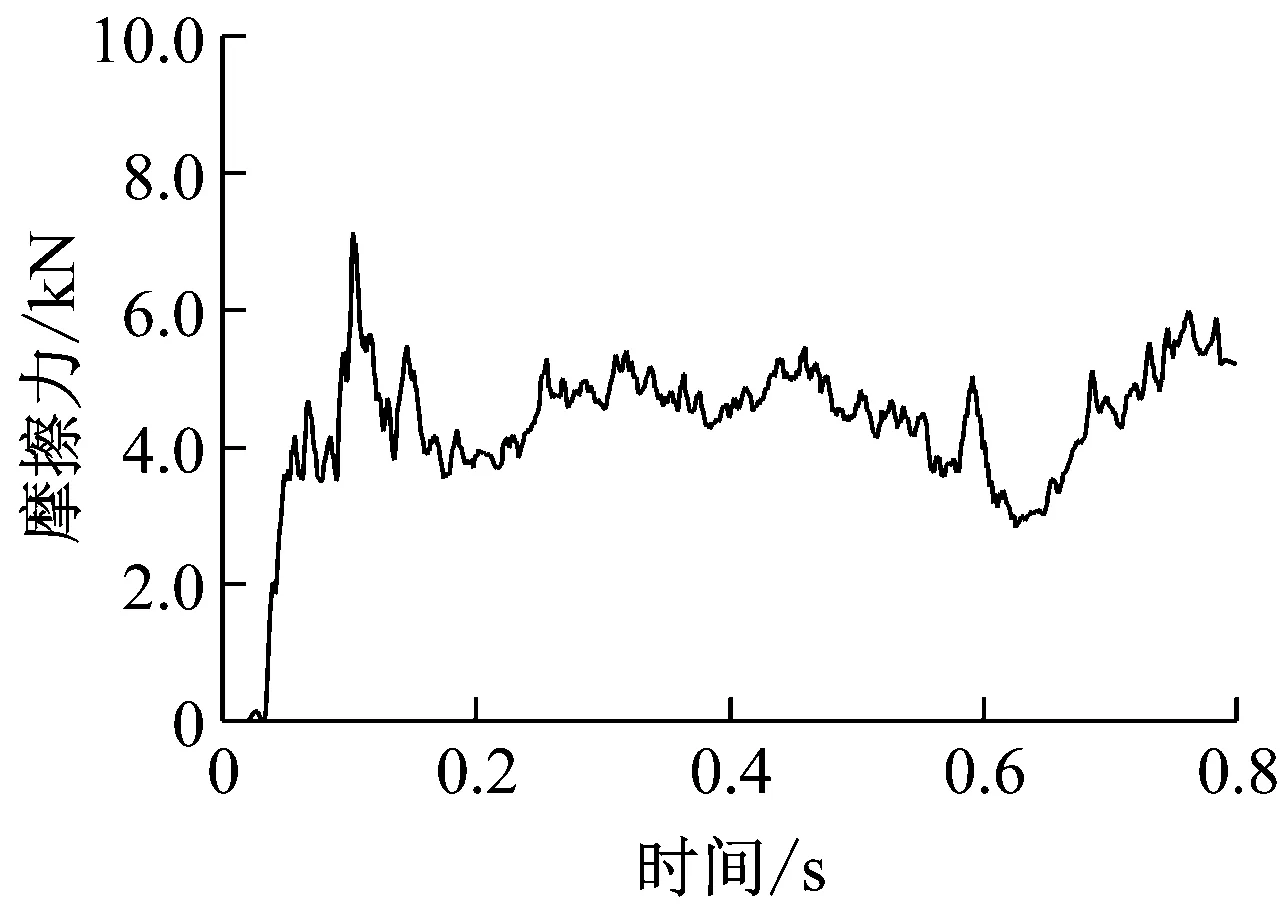
(c) 摩擦力

2.1 管道内径对机器人动力特性的影响

管道机器人舱段长度Lc=350 mm，双万向联轴节长度L2=300 mm，缩径段管道内径D1=250～300 mm，管道机器人和管道其他几何参数以及运动参数与上一工况相同。如图10所示，为管道内径对管道机器人动力特性的影响。随着缩径段管道内径的增加，密封皮碗与管道的接触作用减弱，平均驱动压差减小，4个密封皮碗的峰值等效应力、平均摩擦力单调减少渐进逼近于同一数值。作业舱段的密封皮碗3与弯道的局部挤压作用最强，其等效应力显著高于其他3个密封皮碗；但是，密封皮碗3与弯道的间隙显著高于其他3个密封皮碗，引起的平均摩擦力最小，随着缩径段管道内径的增加，4个皮碗的平均摩擦力的差异逐渐缩小。

(a) 皮碗等效应力

(b) 平均摩擦力

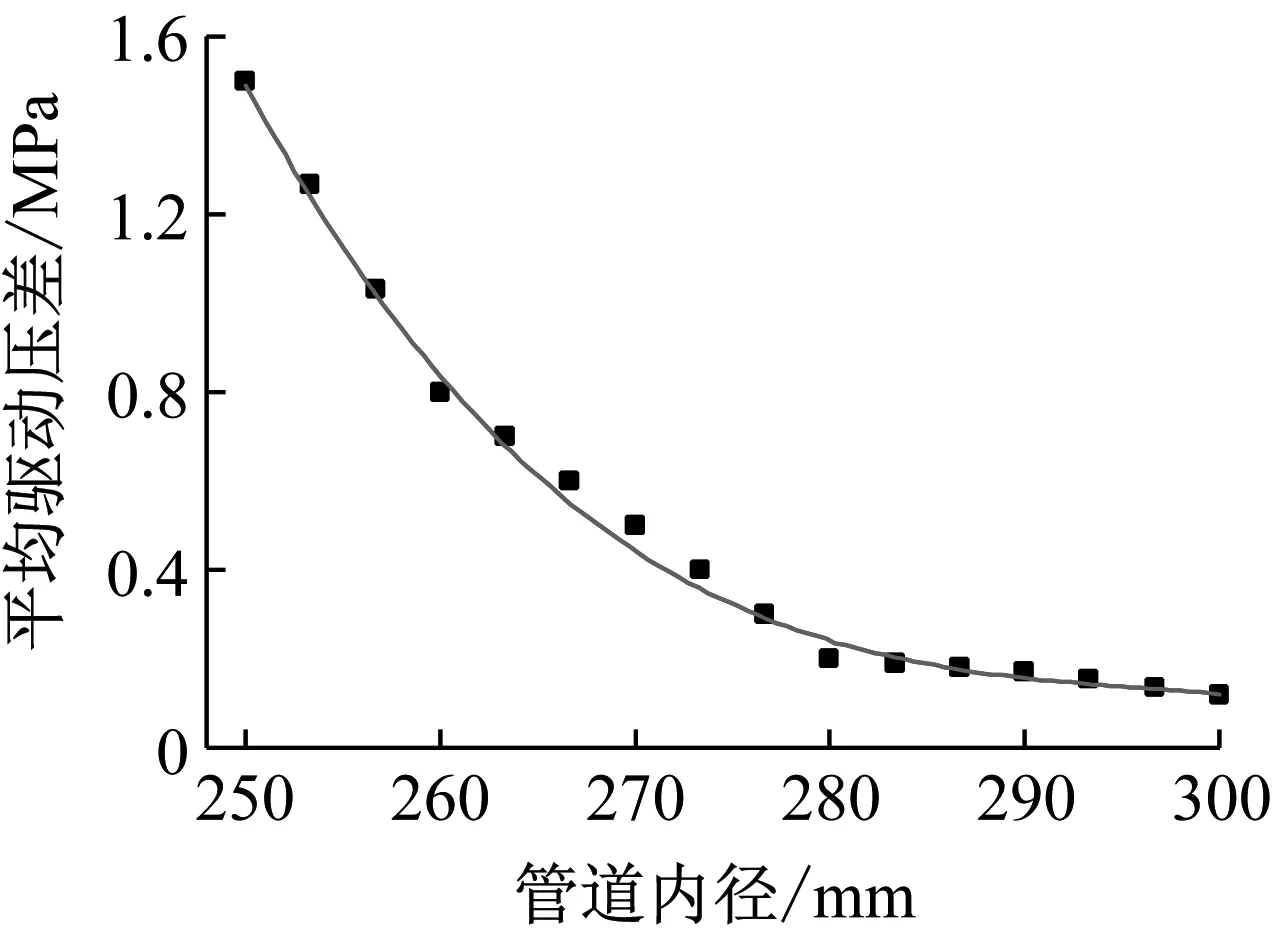
(c) 平均驱动压差

2.2 舱段长度对机器人动力特性的影响

管道机器人舱段长度Lc=350～490 mm，双万向联轴节长度L2=300 mm，缩径段管道内径D1=300 mm，管道机器人和管道其他几何参数以及运动参数与上一工况相同。如图11所示，为管道机器人舱段长度对管道机器人动力特性的影响。随着舱段长度的增加，密封皮碗与管道的接触作用增强，密封皮碗的峰值等效应力、平均摩擦力和平均驱动压差均单调增加。作业舱段的密封皮碗3的等效应力显著高于其他3个密封皮碗；但是，密封皮碗3与管道的平均摩擦力最小。

对比管道内径和舱段长度对于机器人动力特性的影响，两者对于密封皮碗等效应力的量值影响差别不大，但前者对于平均摩擦力和平均驱动压差的量值影响显著高于后者。

(a) 皮碗等效应力

(b) 平均摩擦力

(c) 平均驱动压差

图11 舱段长度对管道机器人动力特性的影响

Fig.11 Effect of cabin length on dynamic characteristics of the in-pipe robot

3 结 论

建立了压差式管道机器人在复杂管道内运行的流固耦合模型，采用CEL方法分析了不同管道内径和舱段长度下的结构动力响应，获得如下研究结论：

(1) 管道机器人随着机器人运动速度的波动和管道拓扑的改变，驱动压差多次出现峰值。管道机器人位于小曲率半径弯道时，管壁内侧对密封皮碗的局部化挤压作用形成峰值等效应力，但是，由于密封皮碗与弯道的间隙引起摩擦力降至谷值。

(2) 随着管道内径的减小和舱段长度的增加，密封皮碗与管道内壁的相互作用增强，密封皮碗的等效应力、平均摩擦力随之增大，平均驱动压差相应提高。

(3) 对比管道内径和舱段长度对于机器人动力特性的影响，两者对于密封皮碗等效应力的量值影响差别不大，但是前者对于平均摩擦力和平均驱动压差的量值影响显著高于后者。