基于三维有限元模型对裂纹非对称转子振动及裂纹扩展控制研究

2019-12-23陈建恩王肖锋

振动与冲击 2019年23期

刘军，胡荣，陈建恩，王肖锋

(1.天津市先进机电系统设计与智能控制重点实验室，天津 300384；2.天津理工大学机电工程国家级实验教学示范中心，天津 300384)

转子是旋转机械的核心部件，现代工业中的很多大型旋转机械，例如燃气轮机、高速压缩机、汽轮发电机组和航空发动机等在运行时转子均要承受高温、高压及交变载荷的作用。长期运行下，由于蠕变和疲劳效应或者机械结构本身存在一些微小的缺陷，易造成转子中萌生微裂纹。如果微裂纹不被及时控制，随着转子长时间的运行，微裂纹就会扩展成较大的裂纹，甚至发生转轴断裂，造成灾难性的破坏[1-3]。因此，对裂纹转子的研究是十分必要的，很多学者对裂纹转子有着深入的研究，但研究对象多为Jeffcott转子[4-5]。

横截面上两个方向的截面主惯性距不相等的转子称为非对称转子。非对称转子在实际设备中有着广泛的应用，例如制有沟槽的发电机转子、涡轮发电机转子、侧面开槽的涡轮离心机和螺旋桨结构等[6]。Ishida等[7-8]研究了非对称转子不稳定振动机理和振动控制方法。马威猛和王建军等[9-10]同时考虑转子和支承的非对称特征，对转子支承系统建立了有限元模型，并分析了转子振动特性。Lazarus等[11]将裂纹对称转子等效为非对称转子，分析在不同转子参数变化下系统的振动响应，忽略了原本结构具有的非对称性。转子裂纹分为开裂纹和呼吸裂纹，由于转子作周期性的旋转，自身结构特点使裂纹会处于时开时闭状态，呼吸裂纹模型更符合实际的裂纹状态[12]。Grabowski[13]提出裂纹方波函数模型，假设转子裂纹的开闭情况符合阶跃函数形式，该模型仅仅考虑裂纹全开和全闭两个状态。Mayes等[14]提出了考虑裂纹开闭过渡过程的余弦函数模型，但它仅以单点表示裂纹的全开和全闭状态，忽略了裂纹全开和全闭的持续过程。高建民等[15]综合上述模型的特点提出了混合函数模型，考虑了裂纹的全开、全闭和半开半闭的过渡过程。尽管应用这些裂纹模型能够表明某些裂纹转子的动力学特性，但是由于事先设定了裂纹在整个转动周期的开闭状态，因此也只是对裂纹呼吸机制的粗略表达。三维有限元建模方法能够更加准确的建立裂纹转子模型，模拟转子在实际的运转过程中裂纹的开闭状态，因此目前在裂纹呼吸机制研究方面应用较多的是有限元模型。Kulesza等[16]采用刚性有限元方法，运用无质量的弹簧-阻尼单元模拟转子的裂纹，研究圆柱轴上裂纹的呼吸和扩展过程。Sharafi等[17]建立裂纹转子的三维有限元模型，依据断裂力学理论研究了裂纹转子弯曲扭转刚度。Liong等[18]用内聚力模型分析了裂纹转子在重力作用下的呼吸效应。Giannopoulos等[19]建立裂纹转子的三维有限元模型，分析在谐波类型的荷载作用下裂缝转轴的局部柔性的变化以及裂缝张开和闭合的呼吸机制。但是三维有限元方法计算速度较慢，为了缩短计算时间，一些学者对有限元模型进行降阶处理，缩减模型的自由度[20-21]。

实现转子系统的振动控制尤为重要。电磁执行器通过实时施加电磁力对转子振动进行主动控制，有效地减小转子振动幅值，提高转子运行的稳定性[22-24]。时浩浩等[25]采用模糊PID控制方法，解决主动磁悬浮轴承系统中由干扰和负载等因素导致的不平衡振动问题，系统具有良好的鲁棒性和抗干扰性。肖闽进等[26]研究了一种模糊参数自适应PID控制方法，该方法超调控制性能优于传统PID控制方法，具有良好的抗扰动性能。Gong等[27]运用模糊PID控制法研究转子轴承系统的振动控制问题。

裂纹的出现削弱转子的刚度，裂纹随转子周期性转动也会显现周期性张开与闭合，长时间运行会加快裂纹的扩展速度。但是，目前的研究尚无法对转子裂纹扩展进行有效的控制，因而对裂纹扩展的研究是十分必要的。Liu等[28]提出了裂纹开闭模型，分析了影响裂纹开闭的一些因素，从而可以对裂纹扩展进行有效控制。但是，该模型间接的利用转子振动特性表示裂纹开闭的相对值，具有一定的局限性。

针对上述问题，本文建立了裂纹非对称转子三维有限元模型，并运用Craig等[29]提出的自由界面模态综合法对模型进行降阶处理，分析了裂纹非对称转子在一定转速范围内的振动响应。利用本文提出的裂纹开闭映射法描述了转子裂纹的开闭状态，并探讨了非对称转子参数的变化对裂纹开闭的影响。运用电磁执行器对裂纹非对称转子进行主动控制，通过仿真分析表明电磁执行器可以有效缩减裂纹非对称转子振动幅值，并且控制裂纹长期处于闭合状态，减小了裂纹对转子刚度的削弱。通过实验结果分析，实验结果与仿真结果基本一致，验证了本文提出的控制方法有效性。

1 裂纹非对称转子有限元动力学建模

1.1 裂纹非对称转子的动力学方程

由于非对称特性的存在，裂纹转子在转动坐标系下的动力学方程可以用线性时变微分方程来表示。裂纹非对称转子的结构简图如图1所示。转动轴设为z轴，转子两端采用水平方向的简单支撑，角速度为Ω，裂纹设置在距左端Lc处，动力学方程表示为：

(1)

式中:M为质量矩阵，K为刚度矩阵，ΩCc为科里利奥矩阵，Ω2Ks为转子转动的软化矩阵，u为转子在转动坐标系下的节点位移，fg、fu和fck分别代表重力、不平衡力和裂纹表面的非线性接触力。

图1 裂纹转子示意图

式(1)中的重力需通过转换矩阵将固定坐标系下的表示变换到旋转坐标系下进行求解。重力矢量在固定坐标系下可以表示为：

(2)

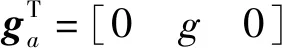
(3)

(4)

式中：EN代表N维单位矩阵，TR为旋转矩阵。

基于非线性接触单元法构建的三维有限元模型如图2所示。在该模型中，裂纹用两个无缝的表面来表示，分别为接触面和目标面。在求解过程中，裂纹处节点的位移设置为边界条件，各节点位移表示为如下公式。

(5)

式中:节点位移可以用两个部分来表示，uck代表裂纹截面处节点位移，uq代表裂纹转子模型中除了裂纹界面的其他部分的节点位移。uc和ut分别表示裂纹面上接触单元和目标单元节点位移。

图2 裂纹转子的有限元模型

非对称轴与横向裂纹位置关系如图3所示。其中，非对称轴的主轴与主坐标系的夹角为φs，裂纹主轴与主坐标系的夹角，文中称为裂纹位置角为φck，在不失一般性的情况下，设定φs为0和φck为φ。

图3 横向裂纹与非对称轴的位置关系

Fig.3 Positional relationship of the asymmetry shaft with transverse crack

1.2 模型的降阶

尽管三维有限元模型在分析裂纹转子的动力学及裂纹呼吸效应问题更加接近实际情况，计算结果也更加准确。但是在处理裂纹等非线性问题时还是具有计算耗时较长、占用系统资源较大和计算效率低等不足。为了克服这些不足,很多研究者提出了一些有效的模型降阶方法，即利用低阶模态集和剩余模态集构造子结构的假设模态集，将界面力作为子结构的广义坐标，并通过位移协调条件消除这组广义坐标来减少计算时间。首先将公式(1)转为一阶状态方程的形式如下：

(6)

(7)

式中:Fg、Fu和Fck为状态力矢量。

在模型降阶过程中，为了获得主模态和剩余模态，令

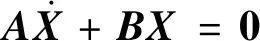
(8)

将X=φeλt代入公式(8)中可得

(λiA+B)φi=0

(9)

式中：λi和φi分别为公式(8)中的特征值和特征向量，由特征向量组成子结构的主模态矩阵Φk。

定义自由界面的状态力矩阵如下：

(10)

式中If为单位矩阵，剩余模态矩阵用Φd表示：

(11)

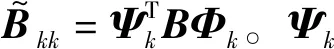
将模型的物理坐标X转化为模态坐标p表示：

(12)

式中：pk和pd分别表示子结构的主模态和剩余模态坐标。

由此，将式(12)代入式(6)整理后得如下表示：

(13)

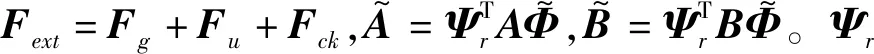
1.3 裂纹开闭映射法

裂纹开闭映射关系如图4所示。在裂纹前缘处建立局部坐标系o1-xyz，图4放大图中j节点的位置在局部坐标系y轴上的投影可直接表示裂纹的开闭程度。

如图4放大图中所示，a为裂纹深度，假设系统仅在弯曲振动作用下裂纹完全张开，jy为裂纹处j节点在局部坐标系y轴上的投影，图中以粗实线表示。当jy>0时，表示裂纹张开，当jy=0时，表示裂纹闭合，jy值越大，表示裂纹张开程度越大。当jy从0增加到jymax以及反向过程分别表示裂纹由闭到开和由开到闭的变化过程。

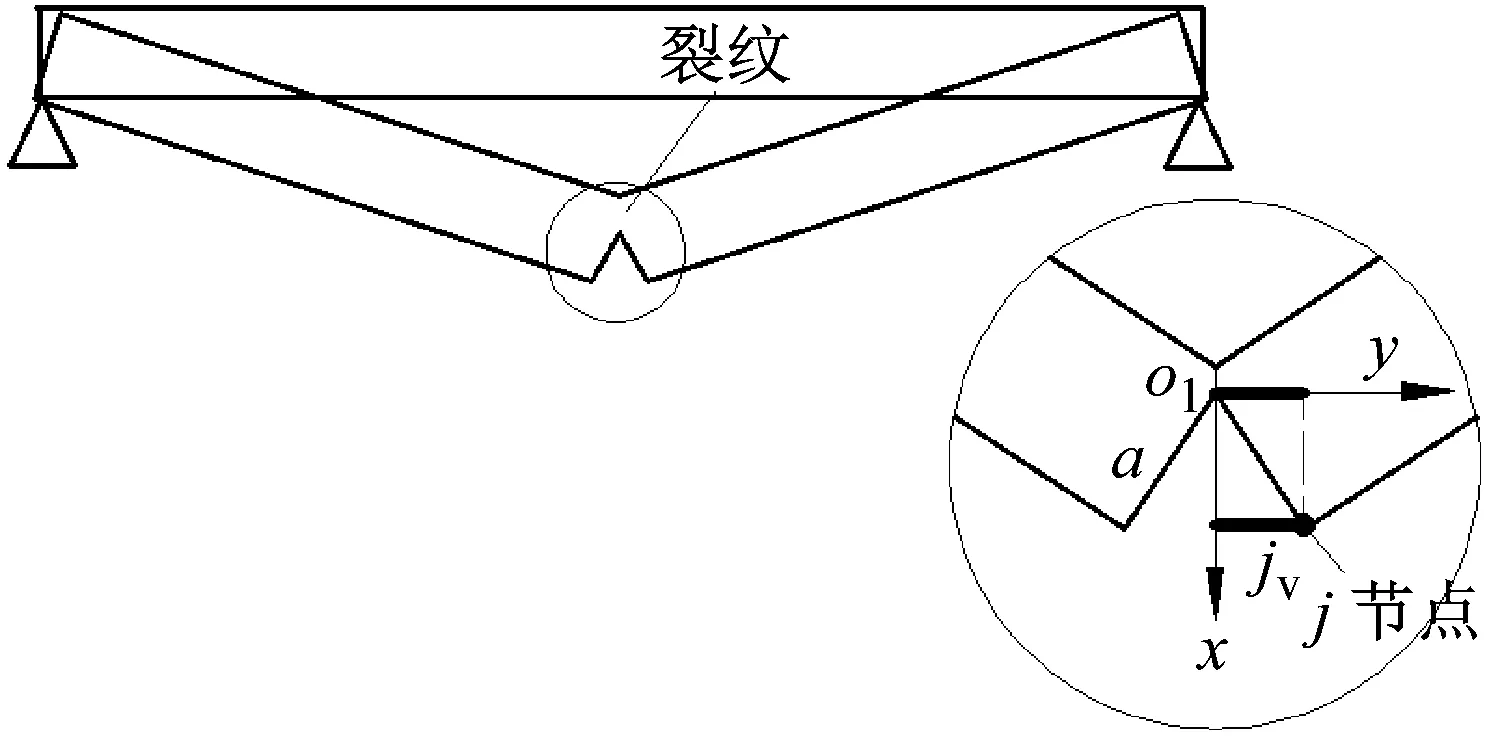
图4 裂纹开闭映射模型

1.4 电磁执行器模型

本文采用8极U型电磁执行器，设计将电磁执行器放置在转子圆盘外侧。U型电磁执行器中相邻的线圈磁极相反，当磁极通电后，相邻位置的磁极构成磁通回路，在四个方向上每对磁极产生吸引力。磁场中以偏置电流I0来保证水平放置的转子的静平衡。如转子位于第三象限时，上下和左右线圈中控制电流分别为I0+ix，I0-ix，I0+iy和I0-iy。通电的线圈在x和y方向上产生电磁合力分别表示为Fmx和Fmy。该电磁合力Fmx和Fmy的表达式如下：

(14)

式中：R0为气隙，I0为偏置电流，ix与iy分别为在x和y方向的控制电流，km和δ为电磁作用器的特征常数。

2 模糊PID控制器的设计

具有电磁执行器作用的转子系统是一个非线性系统，转子系统稳定的工作则需要精密控制。本文采用具有高振动控制灵敏度和抵御外界干扰能力强的模糊PID 控制器。控制系统结构如图5所示，它由两部分组成模糊处理部分和可实时调整参数的PID控制部分。模糊处理部分实现对PID三个参数的自动校正和对非线性电磁合力变动的自学习模糊处理，可调整参数的PID控制部分实现对非对称转子系统的振动控制。

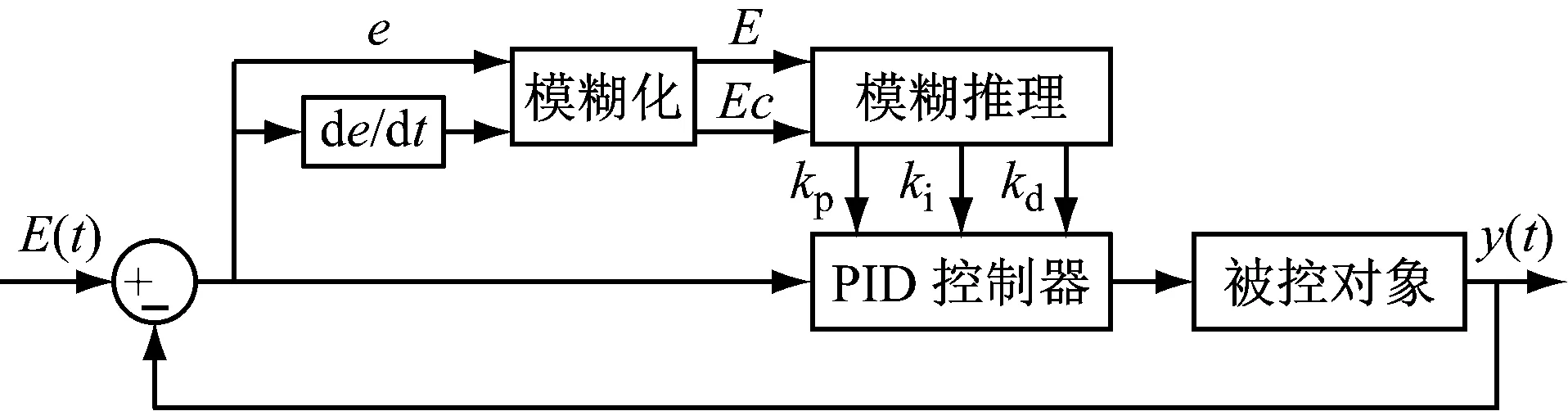
图5 模糊PID控制器结构

2.1 模糊规则

模糊处理器的输入变量是转子系统的位移偏差e和位移偏差变化率de/dt，其模糊空间定义了七个模糊集合，分别为NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)和PB(正大)。模糊处理器的输出变量为PID参数修正量Δkp、Δki和Δkd，通过模糊PID控制器实时输出控制电压U，实时控制电磁铁线圈的电流变化，实现所需非对称转子系统的振动控制的平衡力。根据上述描述，相关参数(语言变量、基本论域、模糊论域及量化因子等)如表1所示。针对非对称转子系统的非线性振动特性，本研究采用并提出了变宽度与变形状的隶属度函数的模糊规则，选用参数e为代表的模糊规则如图6所示。在平衡点附近，该规则采用梯形(高斜率的斜边)隶属度函数，它使系统具有稳定和快速的响应。当转子系统的输入处于变化率小时，其输出变化也会比较低，使控制具有高稳定性。相反，转子在平衡点的远处，该规则采用高斯和三角形隶属度函数，它们的波形变化比较剧烈，使系统具有高的分辨率，当转子系统的输入处于变化率大时，它输出变化比较剧烈，控制误差的分辨率比较高，将转子系统的振动拉回平衡点和使系统具有好的稳定性。

表1 模糊PID参数表

图6 E的模糊定义

2.2 可调整PID参数的获取

模糊PID控制器对PID控制的三个关键参数与输入变量e和de/dt之间的关系，需在控制中实时检测e和de/dt变量并参与模糊计算，以满足输出比例系数kp、积分系数ki和微分系数kd等的实时调整。其中比例系数kp的模糊控制规则如表2所示。由于论文篇幅限制，其它参数ki和kd的模糊规则不在此表述了。

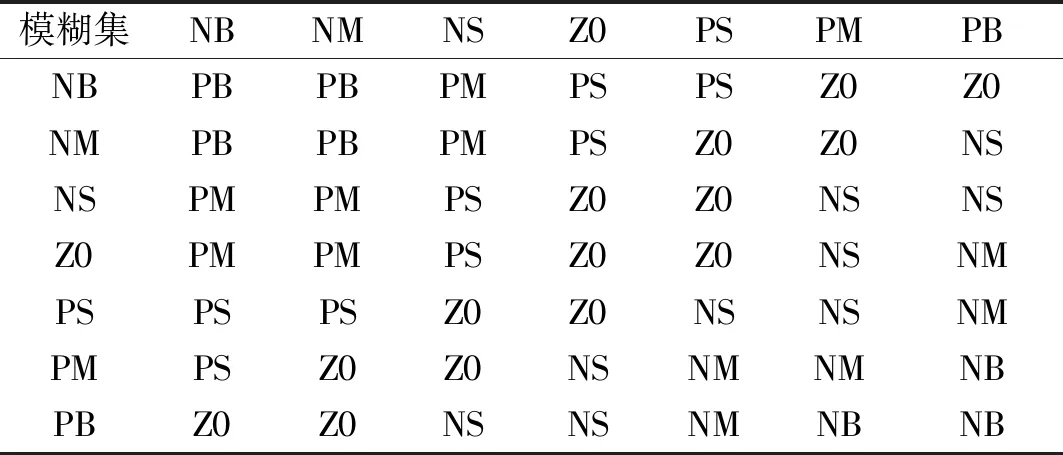
表2 Kp模糊控制表

3 数值仿真

本文通过数值仿真分析了水平放置的裂纹非对称转子的振动特性，呼吸裂纹的开闭状态以及在电磁执行器作用下该转子的振动特性变化及裂纹开闭变化等的情况。重力以及横向裂纹位置是影响裂纹非对称转子动力学特性的重要因素。其相关参数设置如下：转子转盘质量m=8.5 kg，转子长度为L=700 mm，轴半径R=6 mm，裂纹深度为a/R=0.6，转子的偏心质量为mu,距离转轴中心1 mm，衡量非对称转子的扁平性的参数为h,裂纹的位置用LC来表示。转子的材料密度ρ为7 800 kg/m3,杨氏模量为2.06×1011N/m2。对三维有限元模型采用六面体单元进行网格划分，划分成12 111个单元，裂纹表面接触单元沿轴向不考虑摩擦，切向为粗糙接触。另外，在转轴两端各10 mm处添加轴承约束。根据数值仿真，分析研究裂纹非对称转子的共振曲线，裂纹开闭曲线及在电磁执行器作用下的系统振动响应曲线等变化。

3.1 裂纹非对称转子的振动特性分析

3.1.1 裂纹位置角对转子振动的影响

设置不同裂纹位置角的裂纹非对称转子的响应曲线如图7所示，其主共振区域的局部放大图如图8所示。分析图7和图8得知，非对称转子与对称转子的响应曲线有很大的不同，图中三角形的点代表无裂纹非对称转子的共振曲线，矩形和圆形的点分别是角φ为0和π/2时裂纹非对称转子的响应曲线。无裂纹的非对称转子在转速为1 053 r/min处出现主谐波共振，在577 r/min处发生超谐波共振。主共振区域处出现不稳定区域并且近似呈现对称分布，图中用虚线表示的转速范围为不稳定区域。当φ=0，裂纹非对称转子在转速1 047 r/min时发生主谐波共振，在转速为575 r/min时发生超谐波振。当φ=π/2，裂纹非对称转子在转速1 040 r/min时发生主谐波共振，在转速为574 r/min时发生超谐波共振。当非对称转子出现裂纹时，裂纹会削弱转子的刚度，转子的主共振频率和超谐波共振频率变小，转子的振动幅值增大。当裂纹存在时，不稳定区域向左迁移并且不稳定区域范围减小。当φ=π/2,不稳定区域的范围比φ=0时小。

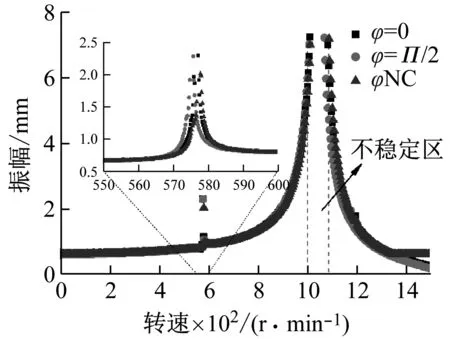
图7 变化裂纹位置角的裂纹非对称转子响应曲线

Fig.7 Resonance curves of cracked asymmetrical rotor with varying crack position angle

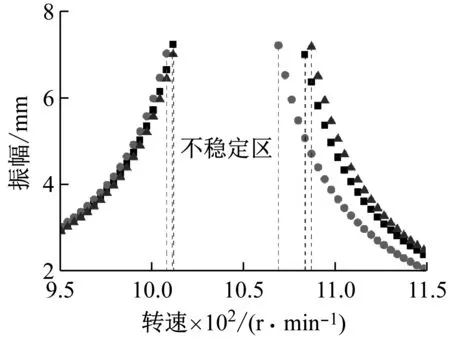
图8 转速在950 r/min～1 150 r/min的响应曲线局部放大图

Fig.8 Local magnification of resonance curves at speeds 950 r/min to 1 150 r/min

3.1.2 裂纹位置对转子振动的影响

设置不同裂纹位置的裂纹非对称转子的响应曲线如图9所示，其主共振区域的局部放大图如图10所示。分析图9和图10得知，矩形、圆形以及三角形的点分别代表图1所示的LC为50 mm、140 mm和230 mm时裂纹非对称转子的共振曲线。当LC增大时，主共振区域内的不稳定区的范围整体向左侧迁移，并且不稳定区域的范围也发生变化，LC为140 mm时该区域最小。在超谐波共振处如图9中放大图可知，裂纹位于中间位置时共振响应范围反而比其它两个位置的大一些，裂纹位于转盘根部的转子的共振响应范围最窄。

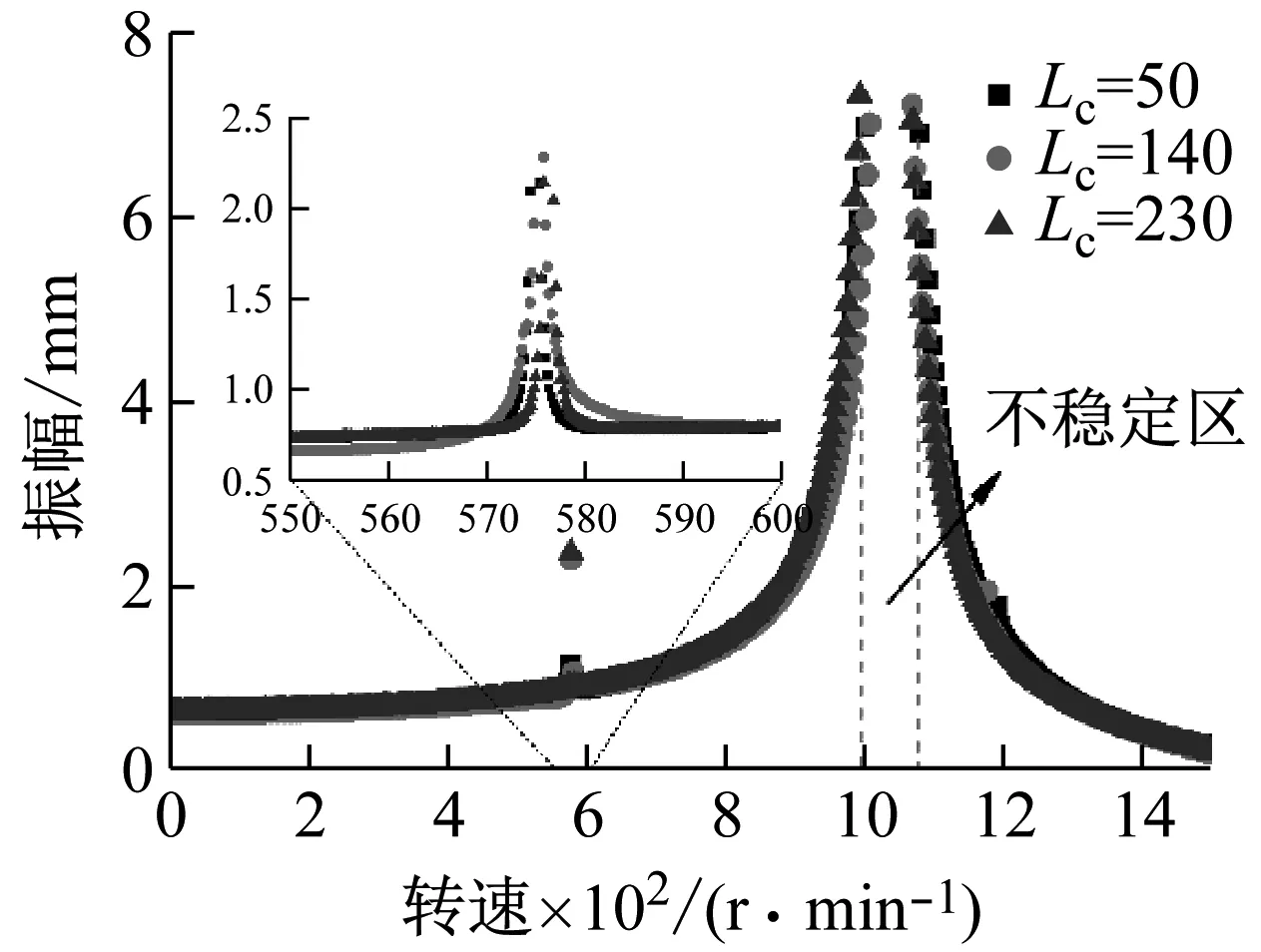
图9 变化裂纹位置的裂纹非对称转子响应曲线

Fig.9 Resonance curves of cracked asymmetrical rotor with varying crack position

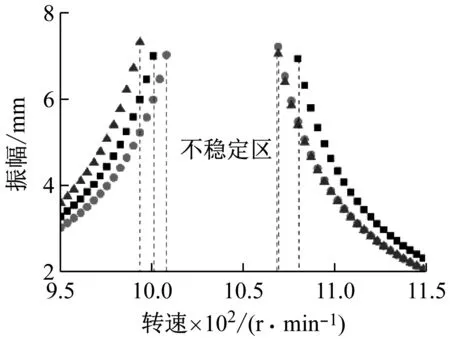
图10 转速在950 r/min到1 150 r/min的响应曲线局部放大图

Fig.10 Local magnification of resonance curves at speeds 950 r/min to 1 150 r/min

3.1.3 非对称转子的扁平性对转子振动的影响

当φ=0时，不同的扁平性裂纹非对称转子的响应曲线如图11所示。圆形和矩形的点分别代表h为8 mm和10 mm时裂纹非对称转子的振动响应曲线。图中虚线范围表示共振的不稳定区域。

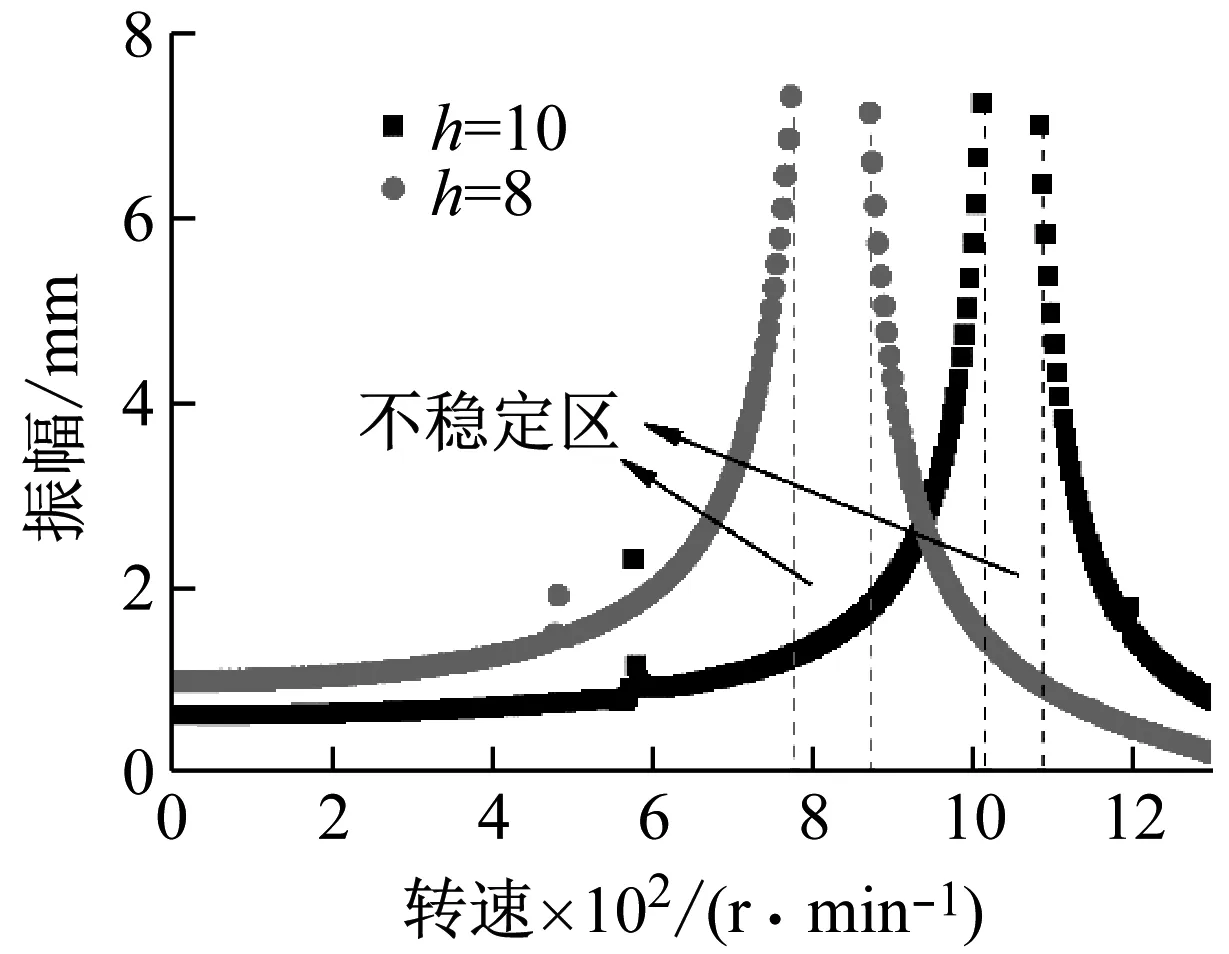
图11 不同扁平性的裂纹非对称转子响应曲线

分析图得知，当h变小时，主共振及超谐波共振的频率都会减小，不稳定区域向左迁移，然而主共振的不稳定区域的范围却增大了。实质上，转子参数如图1所示的h减小时，转轴对于x和y轴的惯性矩差值增大，两个方向的刚度差值增大，裂纹非对称转子的振动幅值相对增加，主共振和超谐波共振的频率相对减小。

3.2 延缓转子裂纹扩展分析

转子裂纹的开闭程度及开闭周期都对裂纹的扩展有着很大的影响，裂纹张开的程度越大，开闭的频率越高，裂纹前缘的材料受周期性疲劳加重，裂纹的扩展速度相对就会越快，裂纹的疲劳扩展程度越大。本文研究了转速、不均匀质量及非对称转子的扁平性对裂纹扩展的影响，可以在实际的转子系统中考虑调整对应参数值，减小非对称转子运动过程中的裂纹开闭程度和开闭周期，从而延缓裂纹扩展。

3.2.1 转速对裂纹扩展的影响

在LC为140 mm时，不同转速下裂纹的开闭程度随时间的变化曲线及周期变化如图12所示，图中横坐标为时间，纵坐标为图4局部图中裂纹处j节点在局部坐标系01-xyz下对y轴方向的映射。图12(a)和(b)分别表示转速为800 r/min和1 200 r/min条件下裂纹的开闭状态，从图中可分析出裂纹的开闭状态呈交替周期性变化，裂纹的开闭程度及开闭的持续时间随转速的变化而变化。从转子转动一个周期分析，裂纹完全张开，完全闭合各一次，呼吸过程具有明显的对称性。裂纹张开的时间比完全闭合的时间长，表明裂纹转子在转动过程中更趋于张开状态。比较图12(a)和12(b)，转速为1 200 r/min时裂纹的张开程度大于转速为800 r/min，表明裂纹的扩展程度越大，裂纹开闭周期变慢。

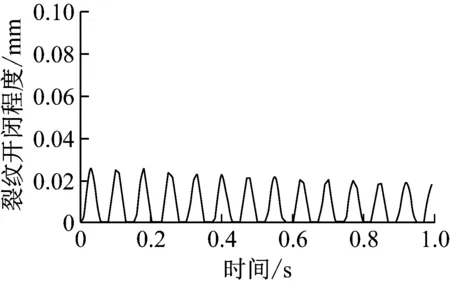
(a) Ω=800 r/min

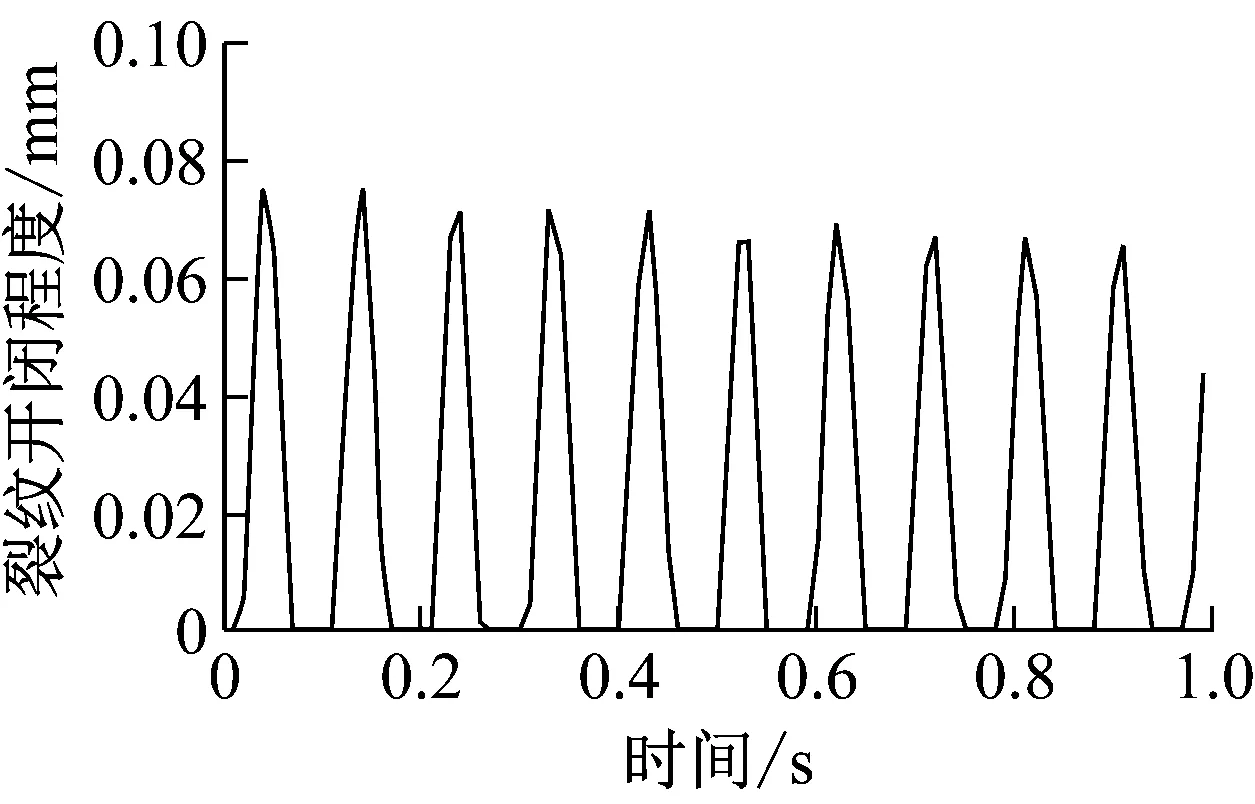
(b) Ω=1 200 r/min

3.2.2 不均匀质量对裂纹扩展的影响

不均匀质量mu=0.05 kg和mu=0.1 kg时裂纹开闭程度随时间的变化曲线如图13(a)和(b)所示。当不均匀质量由0.05 kg增加到0.1 kg时，裂纹的最大张开程度由0.5 mm增加到0.7 mm，并且相同时间内转子裂纹的开闭周期相同。尽管不均匀质量相对较小，但不均匀质量的存在并遇到高转速时将会对转子裂纹的呼吸效应产生较大的影响。所以，转子系统在实际运行过程前可以通过平衡转子的不均匀质量的方法减小其对裂纹开闭的影响，从而延缓裂纹扩展。

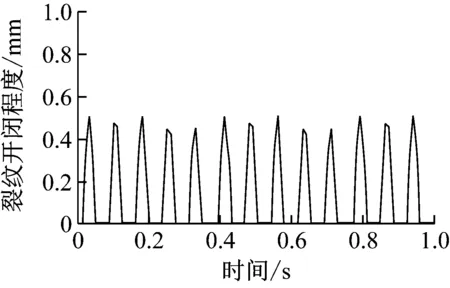
(a) mu=0.05 kg

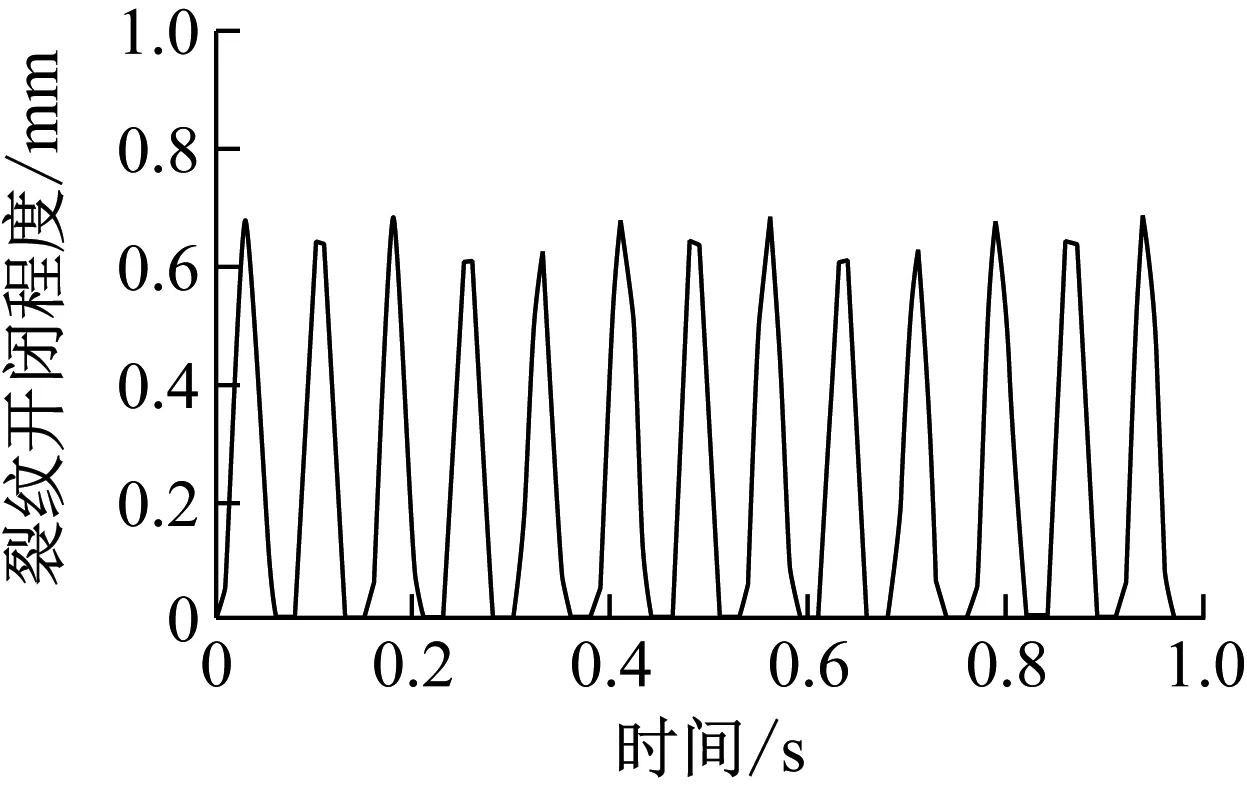
(b) mu=0.1 kg

Fig.13 Effect of unbalanced mass on crack opening and closing degree and period

3.2.3 非对称转子扁平性对裂纹扩展的影响

扁平性参数h为8 mm和10 mm时，裂纹开闭程度随时间变化及周期变化如图14(a)和14(b)所示。当h增大时，裂纹最大的张开程度值减小，裂纹处于张开状态的时间缩短，处于闭合状态的时间增多，且裂纹开闭周期的变化存在。

(a) h=8 mm

(b) h=10 mm

Fig.14 Effect of asymmetrical rotor flatness on crack opening and closing degree

3.3 电磁执行器对转子振动及裂纹扩展的控制

当φ=0时，裂纹非对称转子的响应曲线(矩形的点)如图15所示，而图中圆形的点表示在电磁执行器作用下裂纹非对称转子的响应曲线。分析图得知，在电磁执行器的作用下，裂纹非对称转子在主共振及超谐波共振的最大振动幅值由大共振峰值压制为接近于0的较小的值，并且主共振附近的不稳定区域被消除了。电磁执行器有效的控制了裂纹非对称转子的振动响应。

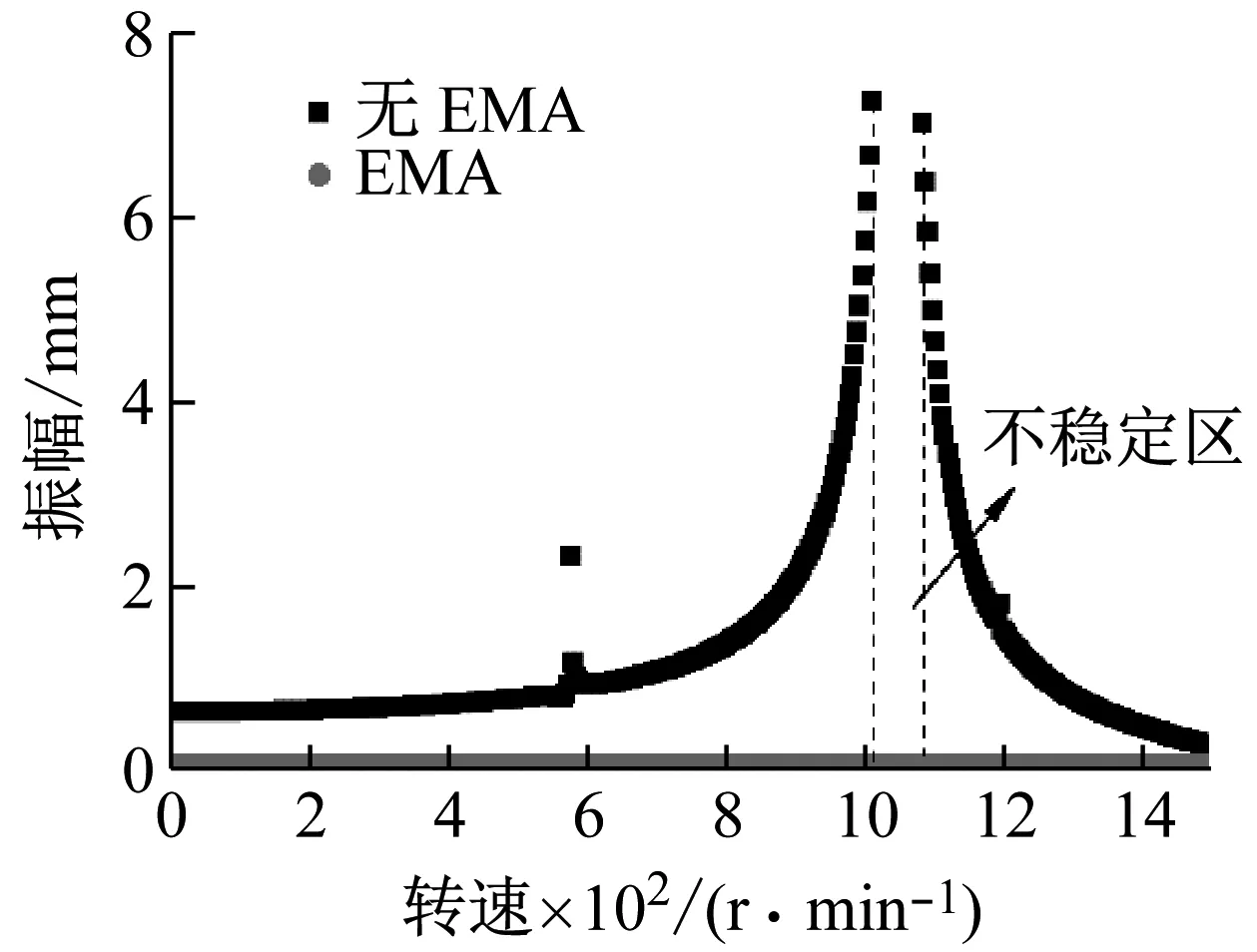
图15 有/无EMA作用的转子振动响应曲线

没有电磁执行器和具有电磁执行器作用情况下的裂纹开闭程度随时间变化曲线如图16(a)和16(b)所示。比较图16(a)和16(b)得知，在电磁执行器作用时，非对称转子中裂纹始终闭合，裂纹周期性开闭现象得到有效的抑制。电磁作用器能很好的控制裂纹开闭状态，从而实现延缓裂纹扩展。

(a) 无EMA

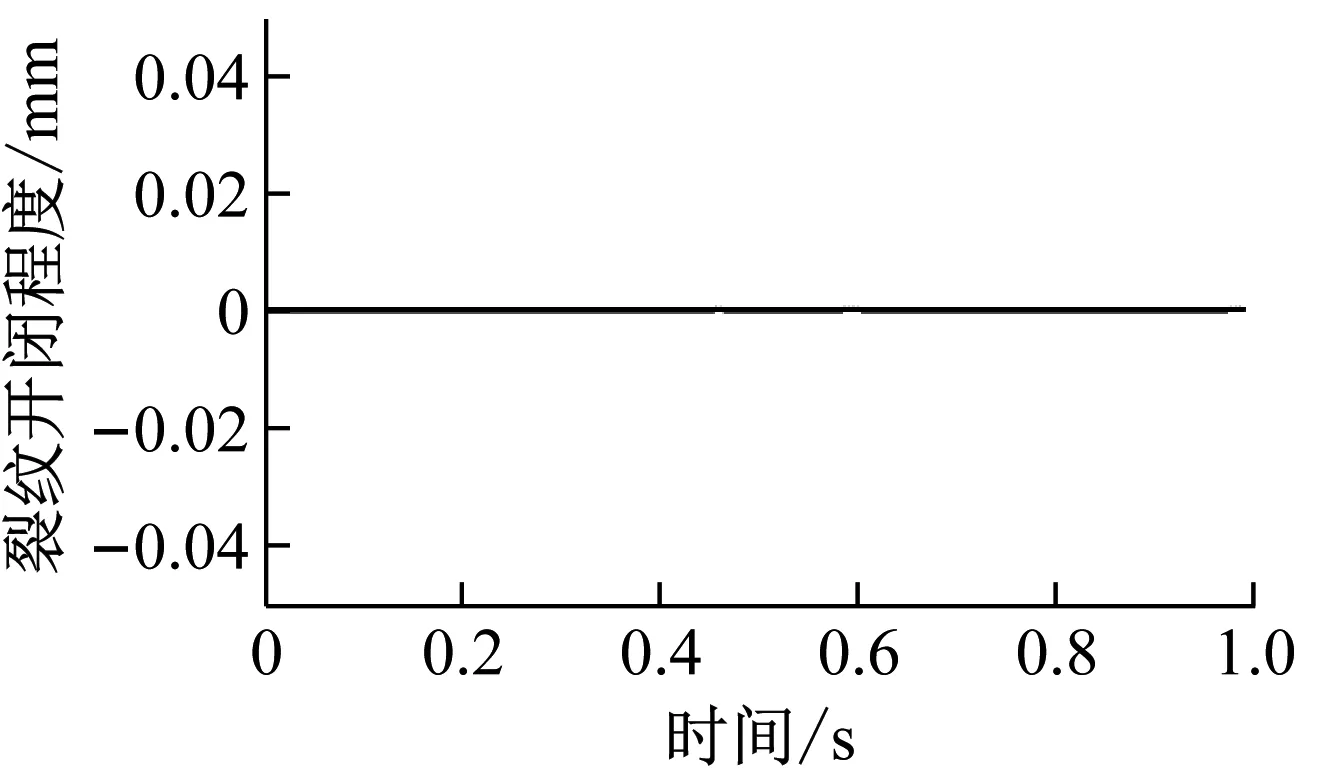
(b) 有EMA

4 实验

实验装置如图17所示，转轴两端采用自动调心球轴承支撑。轴的材料为不锈钢(SUS304)，长度和直径分别为700 mm和12 mm。并在距右端轴承100 mm和300 mm处的轴上分别制作h=9.5 mm长度为100 mm和270 mm的非对称轴体。圆盘(S45C钢)安装在距右端轴承的1/3处，直径和厚度分别为150 mm和25 mm。电磁执行器被安装在圆盘外侧的位置，与圆盘间隔1 mm。为了获得相同特性的横裂纹，在距右端轴承270 mm处设置一个长20 mm深度为3 mm的槽，再将相同材料填充在槽中。电磁执行器如图17(b)所示被安装在与圆盘相距间隙为1 mm的外侧。为安全起见，在距离传感器圆盘右端0.6 mm的位置，加装一个安全轴承。利用分辨率为0.8 μm的涡流式传感器测量转子在x和y方向上的位移。

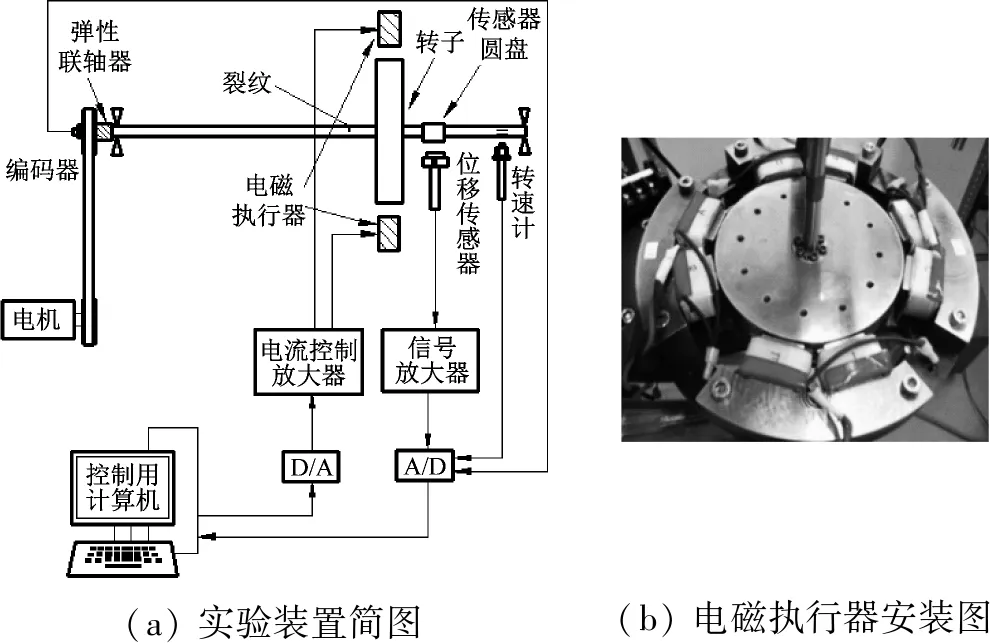
(a)实验装置简图(b)电磁执行器安装图

图17 实验装置

Fig.17 Experimental setup

裂纹非对称转子的实验结果如图18所示。图中圆圈的点表示没有电磁执行器控制时的实验响应曲线，三角形的点表示采用电磁执行器控制时的实验响应曲线。

图18 裂纹非对称转子系统实验响应曲线

在没有电磁执行器作用的情况下，系统在主临界速度Ω=1 020 r/min处产生较大振幅，并出现不稳定区域。当转子转速Ω=408 r/min出现超谐波共振。当引入电磁执行器控制时，系统在整个转速区间(0～1 500 r/min)范围内主共振及超谐波共振都被有效地抑制在低幅值范围，并且不稳定区域被消除。实验结果与前面的图15所示数值仿真结果基本一致。实验表明，电磁执行器能够有效降低转子的振动幅值和消除不稳定区。

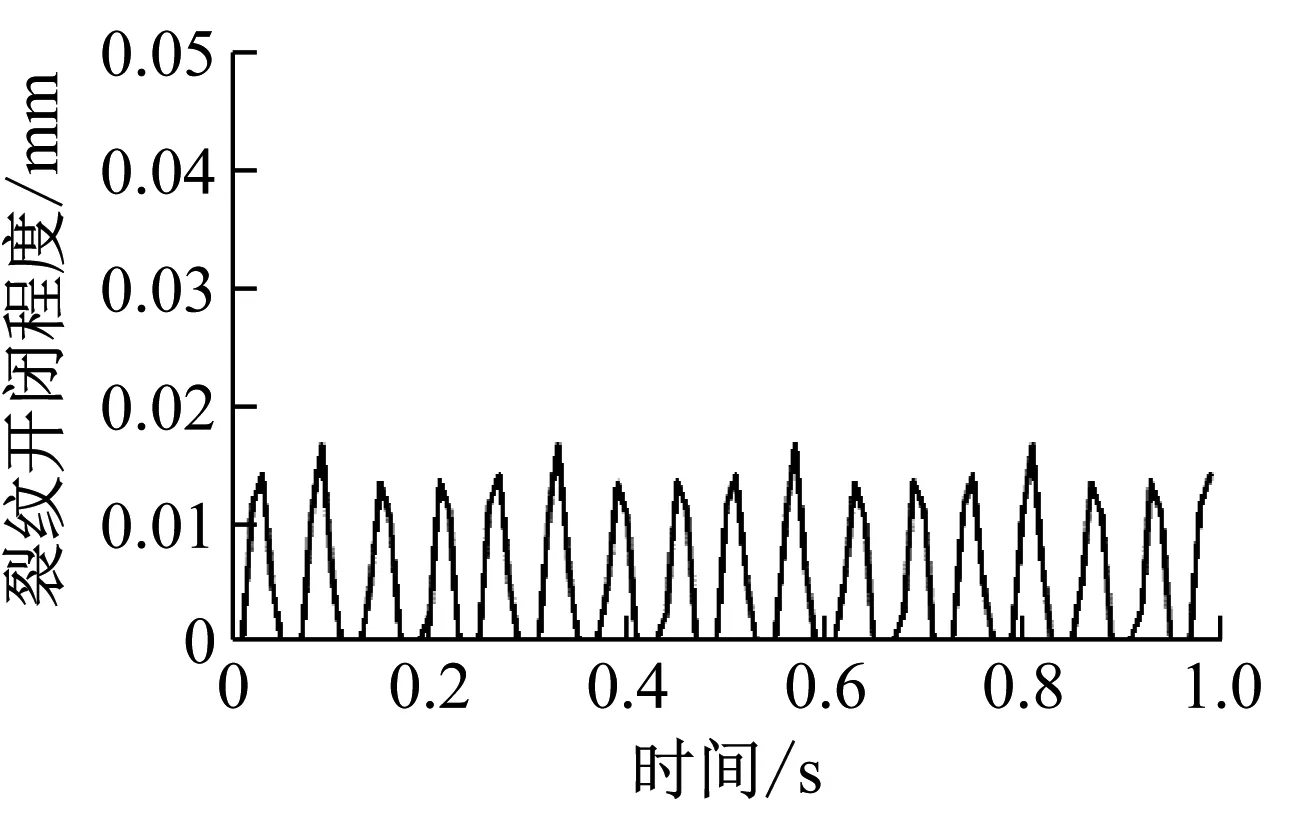
在转速Ω=1 200 r/min时，裂纹非对称转子在有和无电磁执行器作用下裂纹开闭程度的结果如图19所示。该图中虚线表示在无电磁执行器作用时裂纹开闭程度随时间的变化，实线表示在有电磁执行器作用下裂纹开闭程度随时间的变化。在电磁执行器的作用下，裂纹的开闭程度jy的最大值由0.75 mm大幅缩减到0.006 mm左右，同时，相同时间内裂纹一个呼吸周期中处于闭合状态的时间明显增加，裂纹长期处于闭合状态，裂纹的开闭程度得到有效控制，并且延缓了裂纹的疲劳扩展。比较图19与图16(b)得知，实验结果与仿真结果基本一致。