参数异变性对冲击式水电站系统轴系振动摆度影响

2019-12-23许贝贝陈帝伊李欢欢闫懂林

振动与冲击 2019年23期

许贝贝，陈帝伊，李欢欢，闫懂林

(1.西北农林科技大学水利水电科学研究院，西安 712100；2.西北农林科技大学中国旱区节水农业研究院，西安 712100)

近年来，欧洲许多国家和俄罗斯等投入大量财力物力对服役多年水电站重建或改造以提高其服役年限和运行性能[1]。显然，随时间流失，水电站各独立子系统必然出现设备老化、机组振动及噪声变大、绝缘性变差等现象。从非线性动力学角度讲，可认为由各独立子系统结构参数、性能参数等异变性引起水电站轴系振动摆度恶化，即可等价于：水电站系统非线性动力演变已成为水电站轴系振动摆度恶化主要原因。

冲击式水电站由压力引水管道、水轮发电机组及其辅助设备构成的具有复杂水机电磁耦合关系的复杂非线性系统[2-6]，其建模理论与方法的发展经历了从单一领域独立分块建模到多领域统一建模的发展阶段：①各组成模块动力稳定性研究迅速发展，形成较为成熟的单一领域分块建模理论与方法[7-9]；在压力引水管道方面，基于计算流体力学理论，重点研究引水管道内部在恒定流状态→非恒定流状态→恒定流状态过渡过程下压力交替升降过程，即水击过程。解析法、图解法和数值解法是探求该过渡过程下压力变化特征主要求解方法。目前，数值解法作为主流计算水击方法，已被广泛验证其正确性和实用性。在水轮发电机组方面，针对水轮机过渡过程动态特性，可分为外特性法和内特性法。外特性法，往往采用水力机组全特性曲线并联立水轮发电机组运动方程式，通过推求过渡过程线求解水力机组各工况瞬变规律。内特性法，采用水轮机构造参数推求暂态过程下水轮机动态力矩和水头非线性方程，求解水力机组暂态工况下动态力矩和水头变化特征。针对水轮发电机组轴系，重点研究机组在水机电磁耦合作用下轴心轨迹等参数瞬态变化规律。目前，上述计算方法已被国内外大部分学者采用。在机组辅助设备方面，分为机械和和电气两种类型，其目的为有效提高电网安全可靠性，其模型结构可见参考文献[6]。目前，两种类型调速器成为国内外各类水电站重要组成部分。②国内外水力发电系统多领域统一建模理论与方法近年来有明显进展[10-19]；水力发电系统受水力、机械和电磁耦合因素影响，其统一建模体现为多领域及各学科交叉融合趋势。

20世纪70年代前，分数阶微积分理论仅仅是一个数学领域纯理论问题，其详细发展历史过程请参阅具体参考文献[20-21]。1965年，美国耶鲁大学Prof. Mandelbrot提出分形概念。自此以后，分数阶微积分理论被广泛应用于电气工程、机械学、湍流、物理及控制理论、黏弹性动力学和转子动力学等，尤其是分数阶阻尼系统非线性动力学研究，因为分数阶微积分强大记忆特性使得其描述复杂系统非线性动力演化过程更加真实、简洁。Cao等[22]尝试研究分数阶阻尼碰摩转子轴承系统的非线性动力学特征。Yan等[23]通过改进传统整数阶黏弹性模型，提出履带式车辆分数阶模型并从实验上验证其有效性。刘铖等[24]针对双馈风力发电系统设计分数阶自抗扰广域阻尼控制器用以增强互联网电网阻尼控制能力并验证方法的有效性。可见，考虑分数阶阻尼是水电站系统非线性动力演化过程研究所必要的。

综上所述，本文针对冲击式水电站强非线性和多子系统耦合性，引入分数阶阻尼项，在考虑压力引水管道、水轮发电机组和调速设备基础上，建立冲击式水电站分数阶动力学模型，研究分数阶阶次、励磁电流、上导轴承刚度、下导轴承刚度、水导轴承刚度和机组转速参数值变化对机组轴心偏移、旋转速度、喷针行程、水轮机流量和水头的影响规律。

1 考虑分数阶阻尼冲击式水电站模型

1.1 喷嘴流动模型

冲击式水轮机是按动量定理工作的水力原动机，压力钢管内有压流经喷嘴喷入大气之中，形成射流，进而推动水轮机转轮旋转。本文通过对喷嘴模型进行简化，获得结构简图如图1所示。

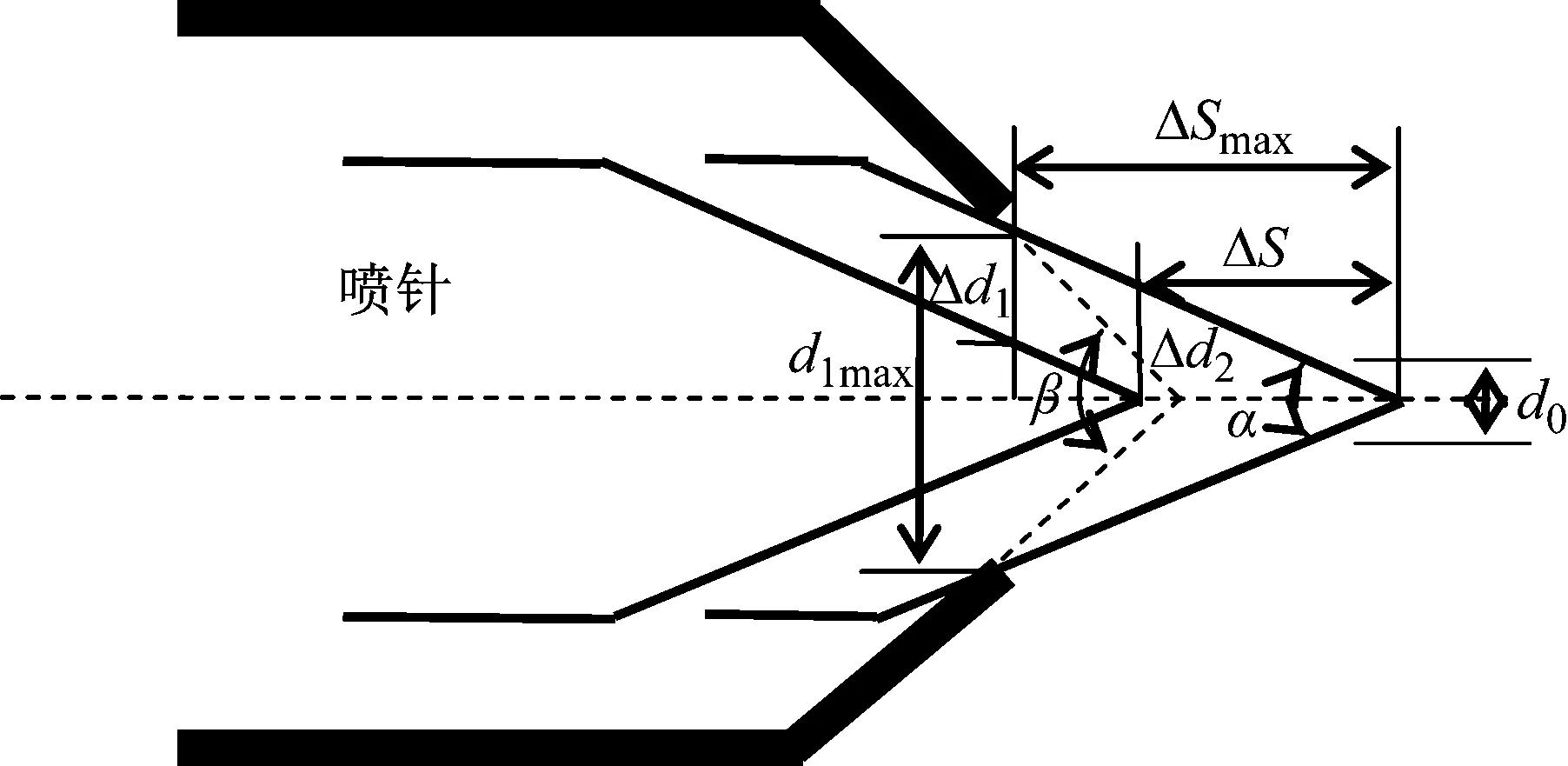
图1 冲击式水轮机喷嘴结构模型

喷嘴流动面积可写为[8]

(1)

根据式(1)，冲击式水轮机流量可表示为

(2)

式中：Q为喷嘴出射流量；V为射流速率；Sj为出射面积；κ为射流系数；Z为喷嘴数目；g为重力加速度；H为水轮机水头。根据式(1)和(2)可得

(3)

式中：q为流量Q相对偏差值；h为水头H相对偏差值。下角标a和b分别表示喷针位置a和位置b。式(3)两边同时对时间t求导可得

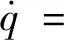
(4)

1.2 压力引水管道模型

引水管道水力损失为[7]

hq=h0-h

(5)

式中：h0为静水头；h为水轮机水头。根据孔口出流原理，压力引水管道出口处流量可表示为

(6)

式中：xr为额定负荷下主接力器位移标幺值。

式(6)两边同时对时间t求导可得

(7)

根据式(5)和(6)，压力引水管道模型可写为

(8)

式中：Te为弹性时间常数；Zn为管道水力浪涌阻抗规格化值。

1.3 发电机负载与调速器模型

发电机负载动态特性可描述为[7]

(9)

式中:Ta为水轮机转动部分惯性时间常数；Tb是负载转动部分惯性时间常数，Tab=Ta+Tb；ω为机组转动角速度；D为发电机阻尼系数。水轮机力矩mt采用IEEE Group提出的简单非线性模型：mt=Ath(q-qnl)-Dtyω。

液压随动系统动态特性可表示为

(10)

式中:Ty为延迟时间常数;kp、ki和kd分别为比例、积分和微分调节增益;s为指令信号;y为导叶开度。

1.4 水轮发电机组轴系模型

通过考虑水力不平衡力重新构建水轮机动力矩与发电机角速度表达式，从而连接水轮机调节系统和水轮发电机组轴系统模型。发电机转子在x方向和y方向受到分数阶阻尼力可描述为

(11)

式中:c为阻尼系数;(x01,y01)为转子轴心在x方向和y方向偏移量;α为分数阶阶次。

机组轴系拉格朗日函数可表示为

L=T-U

(12)

式中:T为轴系动能;U为轴系势能。

根据公式(12)，系统方程可表示为

(13)

式中：MgB为发电机额定转矩；Fx-ump和Fy-ump为x方向和y方向不平衡磁拉力；Fx和Fy为非线性油膜力；Fxf和Fyf为分数阶阻尼力；Fx-rub和Fy-rub为x和y方向碰摩力。不平衡磁拉力和非线性油膜力解析表达式见参考文献[11]，碰摩力见参考文献[15]。根据式(13)，系统方程为

(14)

式中：变量x1、x2、x3和x4为中间变量参数，并无实际物理意义(详见参考文献[5, 25])；变量vx01和vy01分别为转子轴心在x方向和y方向变化速率；变量m1和m2分别为发电机转子和水轮机转轮质量；e1和e2分别为发电机转子和水轮机转轮质量偏心距；r为发电机转子和水轮机转轮形心在水平方向距离；θ和φ分别为发电机转子和水轮机转轮转角；变量k1、k2和k3分别为上导轴承刚度、下导轴承刚度和水导轴承刚度值。

论文中包含四个子系统：压力引水管道子系统、水轮机力矩及发电机子系统、水轮发电机组轴系子系统和调速子系统。其中，压力管道参数和喷嘴流量的耦合可用于水轮机入口处的流量q和水头h，其详细关系见公式(1)；压力引水管道参数(公式(1))与轴系振动方程(公式(3))通过水轮机力矩及发电机参数(公式(2))建立耦合关系，耦联参数包括流量q、水头h、导叶开度y、力矩mt和角速度ω。调速子系统通过发电机角速度与压力引水管道参数建立耦合关系。四个参数详细耦合关系如图2所示，四个子系统模型参数耦合见公式(1)～(4)。

图2 引水管道子系统、水轮机力矩及发电机子系统、水轮发电机组轴系子系统和调速子系统耦合关系

Fig.2 Coupling relationship of pressure penstock, hydro-turbine torque, generator, shafting, and governor

2 非线性动力演化过程

分岔图是系统状态变量与异变参数构成二维空间极限集随参数变化图形，反应系统随参数变化非线性动力演化情况，故可用来表征冲击式水电站轴系振动摆度。本文采用冶勒水电站六喷嘴水轮发电机组参数：算例参数来自于冶勒水电站六喷嘴机组参数。其中，参数HB=580 m,Qb=23.5 m3/s,Z=6;κ=0.985;Zn=1.501 s;Te=0.515 5 s;g=9.81 m/s2;se=0.23 m;d1max=0.085 8 m来自于参考文献[26]。参数m1=1.2×104kg;m2=2.1×105kg;e1=3×10-3m;Mgb=2.25×108N·m;J1=7.9×107;J2=3.5×107s;Tab=10 s来自于参考文献[27]。根据参考文献[28]，发电机阻尼系数D一般视为常数，取值在0～3范围内比较合理，故本文中取值D=0.5；s为参考输入值，s=0。发电机转子和水轮机转轮形心在水平方向距离为估算值，r=0.000 02 m。PID三参数kp=1 s;ki=10 s;kd=3.5 s;均为估算值。转轮质量偏心也为估算值，e2=0.5×10-3m。变量k1、k2和k3分别为上导轴承刚度、下导轴承刚度和水导轴承刚度值。其值对轴系振动摆度值影响很大，故文献中在模型耦合压力引水管道参数后，着重研究其值对轴系振动摆度的影响规律。取值变化范围(107，108)。在超过108值时，轴系振动摆度发散，系统已不可控。系统初值为[x1,x2,x3,x4,x,ω,h,q,x01,y01,vx,vy,φ]T=[0.001,0.001,0.001,0.000 4,0.004,-7×10-9,0.001 34,0.001 021,0.000 001,0.000 001,0,0,0]T。

2.1 励磁电流影响

本节研究不同分数阶阶次下励磁电流值异变对系统动力演化过程影响，如图3所示。

图3 不同分数阶阶次下励磁电流值异变对轴系振动动力演化影响

Fig.3 The shaft vibration versus the excitation current with different level of fractional order

从图3可总结以下四方面结果：①不同分数阶阶次下，系统动力失稳所对应的阈值不同，但最终都会经随机振动态进入到不可控态；②分数阶阶次取值不影响系统动力演化方式，演化方式均是通过振动态→随机振动态→不可控态；③励磁电流对系统动态动力演化过程影响很大，但从电站运行角度，在励磁电流异变值不超过阈值情况下，水电站轴系振动摆度均满足电站运行要求；④随励磁电流逐渐增大，轴心偏移量增大，机组振动增强，且影响程度很大，极易引发碰摩事故。振动态进入随机振动态阈值(定义阈值A)随分数阶阶次变化情况如图4(a)所示。随机振动态进入不可调态阈值(定义阈值B)随分数阶阶次变化情况如图4(b)所示。

观察图4，分数阶阶次取值对阈值A影响不大，基本在740 A左右变化；分数阶阶次取值对阈值B影响很大，整个变化范围可延展至(750，2 750)A，且具有先突然增大后逐渐减小变化规律。

2.2 上导轴承刚度影响

本节研究不同分数阶阶次下上导轴承刚度异变对轴系振动动力演化过程影响，如图5所示。

观察图5，随上导轴承刚度减小，机组振动在维持一段时间等幅振荡后，最终通过随机振动态进入不可控态。当α=1.00，阈值A所对应上导轴承刚度值最大；当分数阶阶次增加或减小，阈值A值均会减小。当α取值小于0.9或大于1.1，系统动力演化方式也发生了变化，出现由稳定直线过渡到连续波动状态并逐渐进入随机振动态趋势。

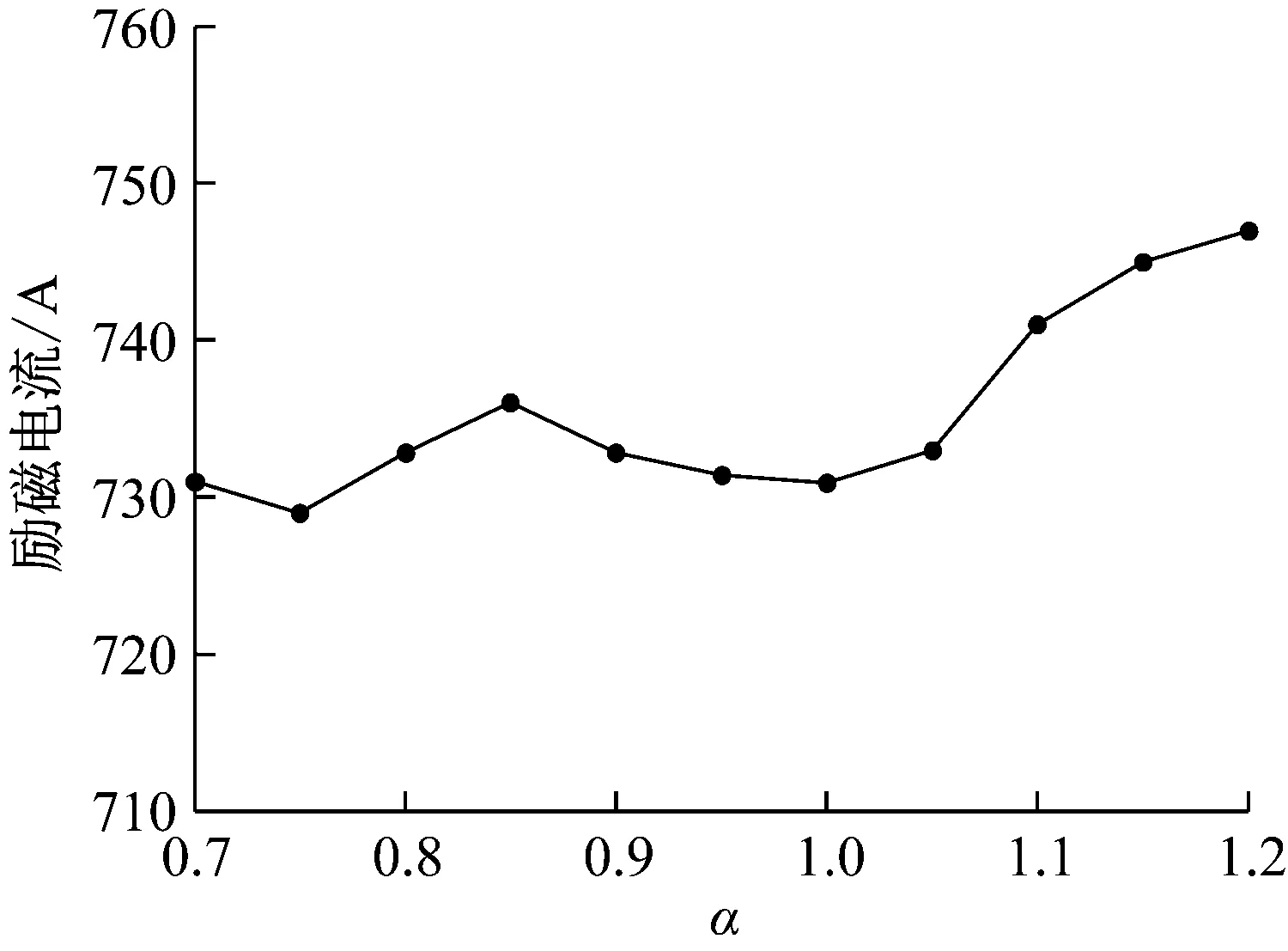
(a) 周期振动进入点移动情况

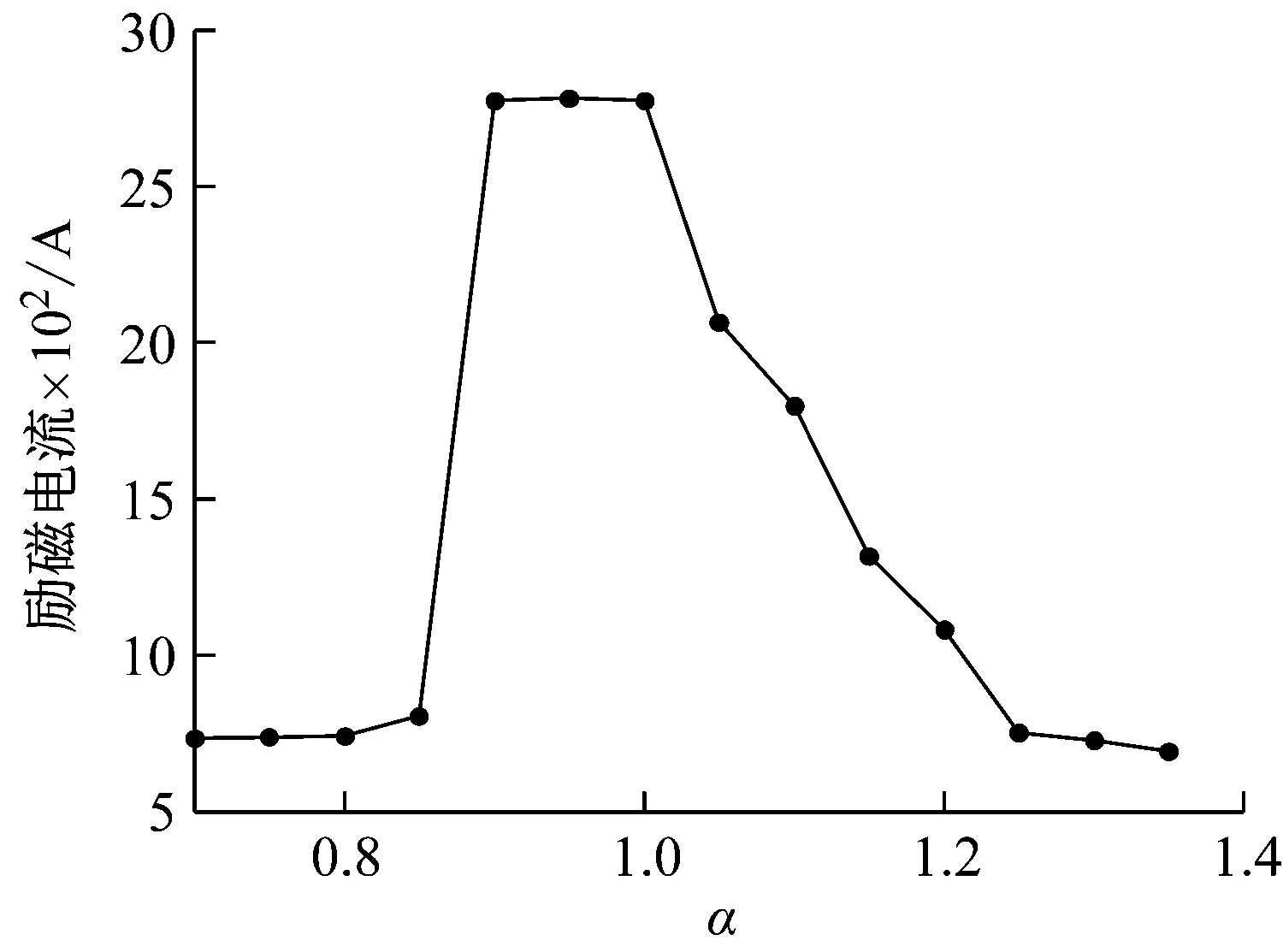
(b) 随机振动进入点移动情况

图4 不同分数阶阶次下系统进入振动周期态和随机振动态所对应励磁电流值的移动情况

Fig.4 The bifurcation points versus the excitation current with different level of fractional order

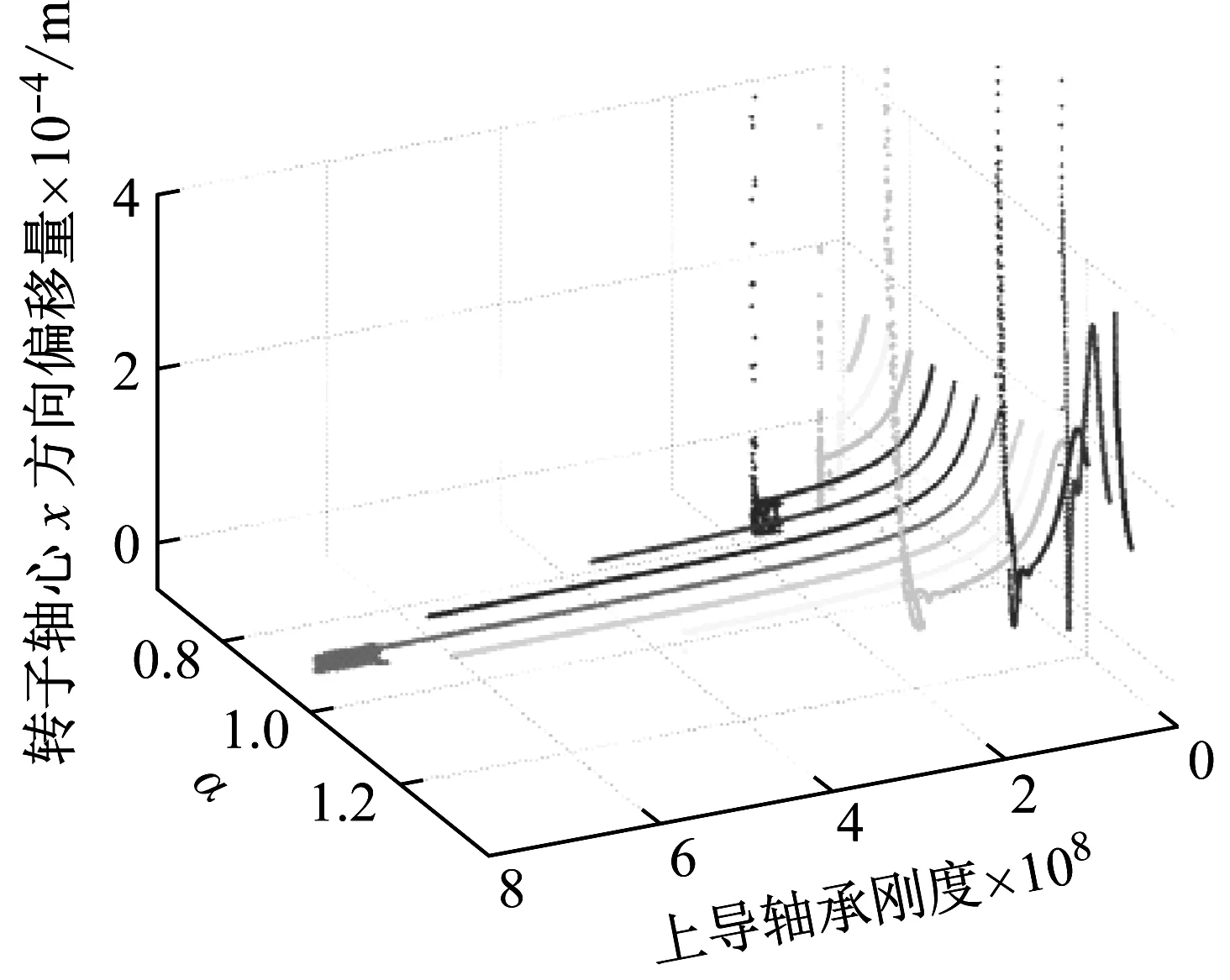
图5 不同分数阶阶次下上导轴承刚度异变对系统动力演化过程影响

Fig.5 The shaft vibration versus the stiffness of upper guide bearing with different level of fractional order

2.3 下导轴承刚度影响

本节研究不同分数阶阶次下，下导轴承刚度异变对系统动力演化过程影响，如图6所示。

观察图6，随下导轴承刚度增加，改变分数阶阶次对系统动力演化过程影响很大，但均以Hopf分岔形式失去稳定。具体来说，α分别取0.75、1.20和1.25时，系统失稳后均直接进入随机振动态；α分别取0.80、0.85和1.15时，系统通过周期振荡直接进入大幅度随机振动态。当α分别取0.90、0.95、1.00、1.05和1.10时，系统通过周期振荡先进入小幅度随机振动状态，而后进入大幅随机振动态。

图6 不同分数阶阶次下下导轴承刚度异变对系统动力演化过程影响

Fig.6 The shaft vibration versus the stiffness of lower guide bearing with different level of fractional order

2.4 水导轴承刚度影响

本节研究不同分数阶阶次下，水导轴承刚度异变对系统动力演化过程影响，如图7所示。

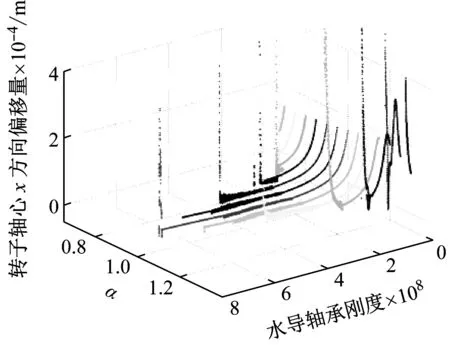
图7 不同分数阶阶次下水导轴承刚度异变对系统动力演化过程影响

Fig.7 The shaft vibration versus the stiffness of water guide bearing with different level of fractional order

水导轴承刚度变化和下导轴承刚度对系统轴系振动摆度影响相似，这里不进行详细描述，主要介绍不同之处。在α=0.95时，随水导轴承刚度增加，先出现Hopf分岔，接着进入稳定周期振荡，进而进入一个小幅度随机振动态；α分别取值0.95、1.00和1.05时，系统在小幅度随机振荡后并未直接过渡到大幅度随机振荡态，而是进入周期振荡，最后由周期振荡直接进入大幅度随机振荡态。

2.5 发电机角速度轴心动态演化过程

在机组发生故障后，很容易发生机组失速故障，机组转速升高后会出现剧烈振动行为。机组轴心轨迹图可用于分析机组失速后动力演化过程。图8描述机组转动角速度从0～850 rad/s变化轴心轨迹动力演化过程。

(a) 0<ω<200

(b) 200<ω<700

图8 机组转动角速度从0～850 rad/s变化轴心轨迹动态演化过程

Fig.8 Dynamic evaluation of the center of the generator rotor when the generator speed changes in the interval (0, 850) rad/s

观察图8(a)，在0<ω<7 rad/s时，机组振动幅值基本为0 m；在7<ω<44 rad/s时，机组振动幅度随转速线性增加；在44<ω<55 rad/s时，振动幅度基本保持不变，且在ω=55 rad/s转速发生了跳跃现象；在55<ω<189 rad/s时，振动幅度随着转速增加迅速增加，并在ω=189 rad/s达到该阶段峰值；在189<ω<194 rad/s时，振动幅度迅速衰减，振动幅度减小，在194<ω<250 rad/s时，振动幅度基本不变。观察图8(b)，在250<ω<269 rad/s时，振动幅度基本不变；在269<ω<299 rad/s时，振动幅度略有增加，且在ω=299 rad/s时出现跳跃式下降；在299<ω<343 rad/s时，振动幅度先减小后趋于稳定，且在ω=343 rad/s跳跃式上升，之后随转速升高振动幅度先上升后下降；当401<ω<603 rad/s时，随转动角速度缓慢上升，振动幅度缓慢上升趋势；在517<ω<530 rad/s，振动幅度先是跳跃式下降，紧接着出现跳跃式上升，且幅度大于之前幅度；在603<ω<700 rad/s时，振动幅度也随转速增加缓慢增大。观察图8(c)，当700<ω<850 rad/s时，机组振动幅度刚开始缓慢增加，最后振幅迅速升高并达到最大值。