行星齿轮箱齿轮磨损故障诊断
2019-12-23李海平赵建民倪祥龙
李海平,赵建民,张 鑫,倪祥龙
(1.军事科学院 系统工程研究院,北京 100141;2.陆军工程大学 装备指挥与管理系,石家庄 050003;3.中国洛阳电子装备试验中心,洛阳 471003)
行星齿轮箱与定轴齿轮箱相比,前者可以在相对狭小的空间内提供更大的传动比因而被广泛应用于如风机、直升机、起重机等大型复杂机械设备之中。然而,长时间低速重载的工作条件以及其结构上的特殊性也使相应的故障诊断工作具有自身的特点和难点[1-2]。
传统的行星齿轮箱故障诊断方法从动力学建模的角度分析其正常运转及各部件故障发生机理,然后分析各种故障对应的频谱总结出规律来进行故障诊断[3-7]。这种故障诊断方法对专业性要求比较高,需要对行星齿轮箱的结构特点和故障对应的频谱规律有比较透彻的理解。近年来研究比较多的是一些智能的故障诊断方法,通常包括信号采集、信号处理、特征提取和智能分类等。Paul等[8]介绍了基于振动的直升机传动机构故障诊断有关研究综述,包括常用的特征参数和故障诊断技术等。Liu等[9]提出一种核聚类分析方法来实现特征选择和不同严重程度的行星齿轮箱齿轮磨损故障诊断。Feng等[10]利用集合经验模态分解和能量分离方法实现风机行星齿轮箱的故障诊断。这些智能故障诊断方法通常需要进行信号处理和特征提取,需要一定的专业基础,同时有些方法计算过程很复杂,不易于应用。
深度学习因可以直接将采集到的原始振动信号输入到模型之中,而不需要进行特征提取和选择这类要求具备专业知识的信号处理过程而被广泛应用。深度置信网络(Deep Belief Networks,DBN)作为第一个提出的深度学习训练算法,不管在应用还是算法的改进都有广泛的研究,是目前研究和应用都比较广泛的深度学习结构[11]。He等[12]提出一种基于DBN的齿轮传动系统故障诊断方法,取得了很高的故障诊断准确率。然而,在应用DBN时,原则上训练集和测试集的每个样本要包含设备运转至少一个周期的数据,即确保每个样本能包含足够反映设备状态信息的数据。在采集设备振动信号的过程中,如果采样频率比较低则可能导致一个周期数据不足以反映设备状态,所以采样频率通常很高,这就导致每个样本的数据点数比较大。而DBN要求的训练样本量又很大,训练样本多、输入数据维度大,造成DBN的训练时间非常长。因此,将DBN应用到机械系统故障诊断领域需要解决的首要难点问题就是在保证诊断准确率的前提下减少训练时间。
减少智能诊断模型训练时间最常用也是最有效的方法就是数据降维,将原本维度很高的样本降至比较低的维度来减少计算量从而缩短训练时间,特征提取可以算是数据降维的典型代表。主成分分析(Principal Component Analysis,PCA)方法由于易实现且概念简单等优点被广泛应用于数据降维。为了提高诊断精度,在应用PCA时通常要分析多个传感器采集到的信号。如果只是简单叠加多路信号的PCA分析结果直接作为诊断模型的输入,就没有考虑各路信号之间的联系,也会影响诊断精度。欧氏距离技术(Euclidean Distance Technique,EDT)是使用较为广泛的表示二者之间距离关系的算法,其同样具有理论知识简单且计算速度快的优点。
因此,本文利用PCA方法实现数据降维,然后采用EDT计算结果表示多个传感器信号的PCA结果之间的关系,将两种结果作为样本输入到DBN模型中得到诊断结果。该方法理论简单易懂,算法易于实现,计算结果准确,而且大大减少了计算时间。
1 基于DBN的传统方法分析
本节对基于DBN的传统故障诊断方法进行研究,主要分析基于原始数据、FFT和特征参数三种情况下的DBN诊断性能。在分析过程中借助行星齿轮箱齿面磨损预置故障实验数据来进行。
1.1 行星齿轮箱齿面磨损预置故障实验
实验系统如图1所示,由实验用行星齿轮箱、三相异步电磁调速电机、风冷磁粉制动器、转速转矩传感器以及组成。该齿轮箱为单级行星齿轮箱,由1个太阳轮(齿数为13)、3个行星轮(齿数为64)和1个齿圈构成(齿数为146),传动比为12.5,其内部结构如图2所示。

图1 行星齿轮箱实验台

(a)

(b)
实验共预置了太阳轮、齿圈和行星轮单个轮齿齿面磨损三种局部故障,故障程度统一设置为轮齿长度的1/2和宽度的1/2,如图3所示。分别对正常状态和三种故障状态开展了实验,采样频率和采样时间分别为20 kHz和12 s,转速设置为400、800和1 200 r/min-1,每种转速负载设置为0、0.4、0.8和1.2 Nm,每种工况采集33个样本。关于该实验的更多具体信息可以参考文献[2],此处不再赘述。
1.2 基于原始数据-DBN的诊断方法
基于原始数据的DBN诊断方法是对采集到的振动信号进行归一化后直接输入到DBN模型之中进行分类诊断。下面对采集到的数据进行分析:
为了与作者之前的研究成果对比,本文同样选择转速为1 200 r/min、负载为1.2 Nm工况下的太阳轮故障、行星轮故障、齿圈故障和正常状态四种状态信号进行分析。该数据分为四种状态,每种状态有33个样本,每个样本有4列振动信号,每列信号有12×20 000=240 000个数据点。为了提高计算速度并保证诊断精度,选择包含每个齿轮一个运转周期的采样点数(2 000个)作为一个训练样本或测试样本,则每种状态有3 960个样本。采用K倍交叉验证方法(即将所有样本分成K份,K-1份用于训练,1份用于测试),取K=10,则训练样本数为14 256个,测试样本数为1 584个。将数据归一化后输入到DBN模型之中。

(a) 太阳轮

(b) 行星轮

(c) 齿圈
研究发现,对DBN分类能力影响较大的参数有三个:隐藏层数(l)、隐藏层单元数(u)和批尺寸(batchsize)(b)。对于隐藏层数,本文主要研究RBM数量为2、3、4、5这四种情况,再增加层数会导致计算量太大,意义不大。对于隐藏层单元数和批尺寸的取值目前尚未见到有明确的结论,本文经过探寻作如下设定:
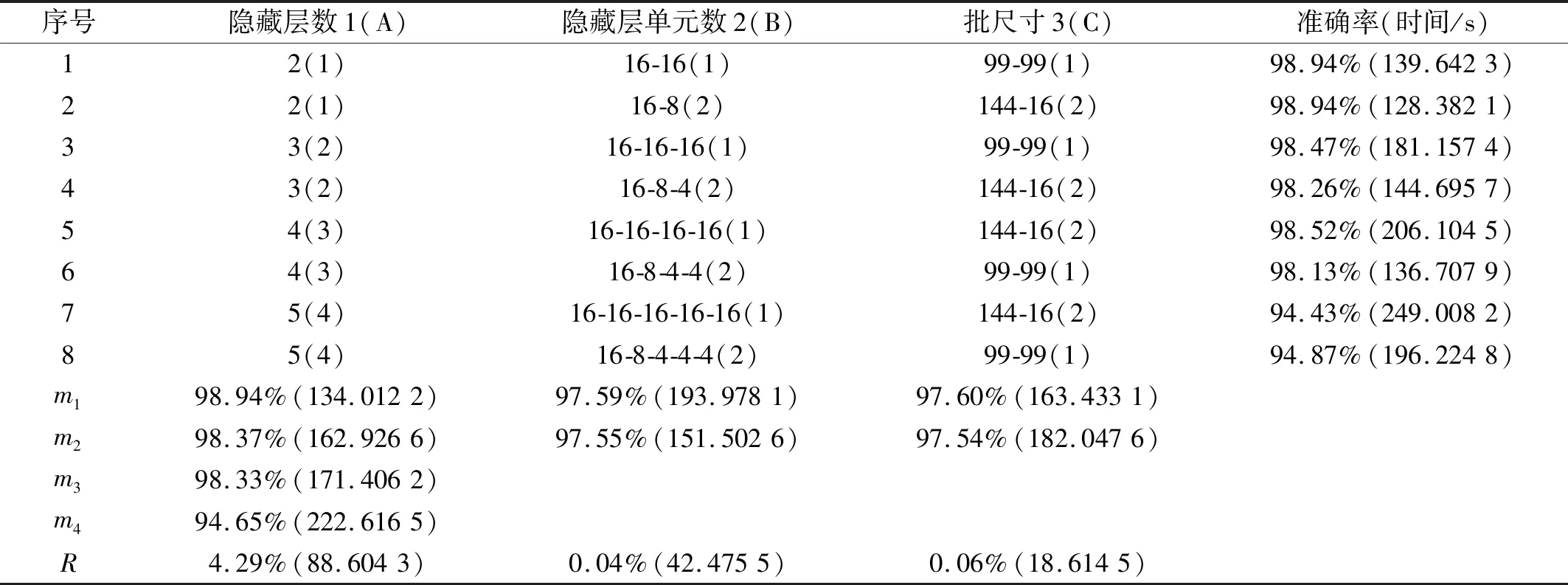
(1) 隐藏层单元数
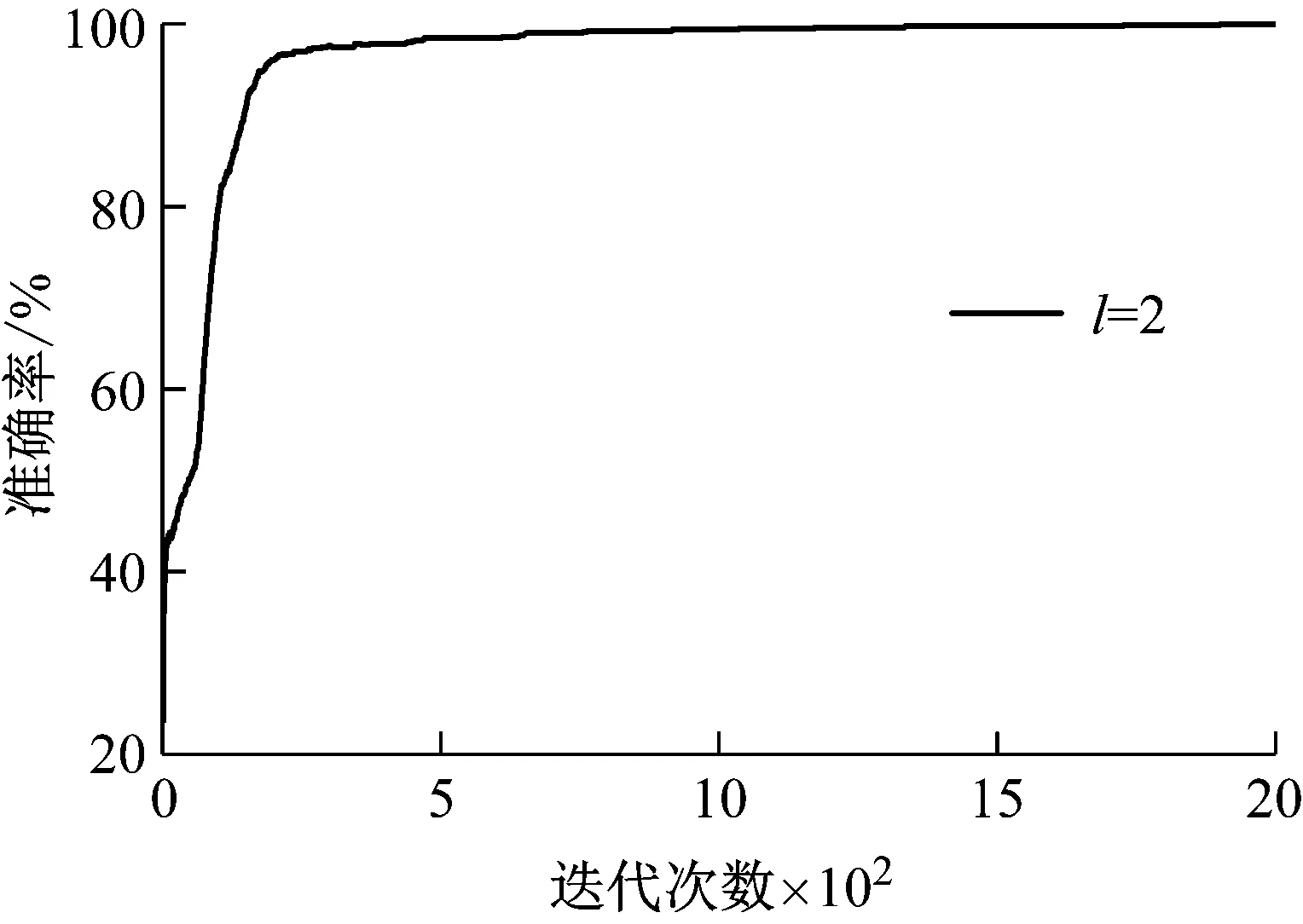
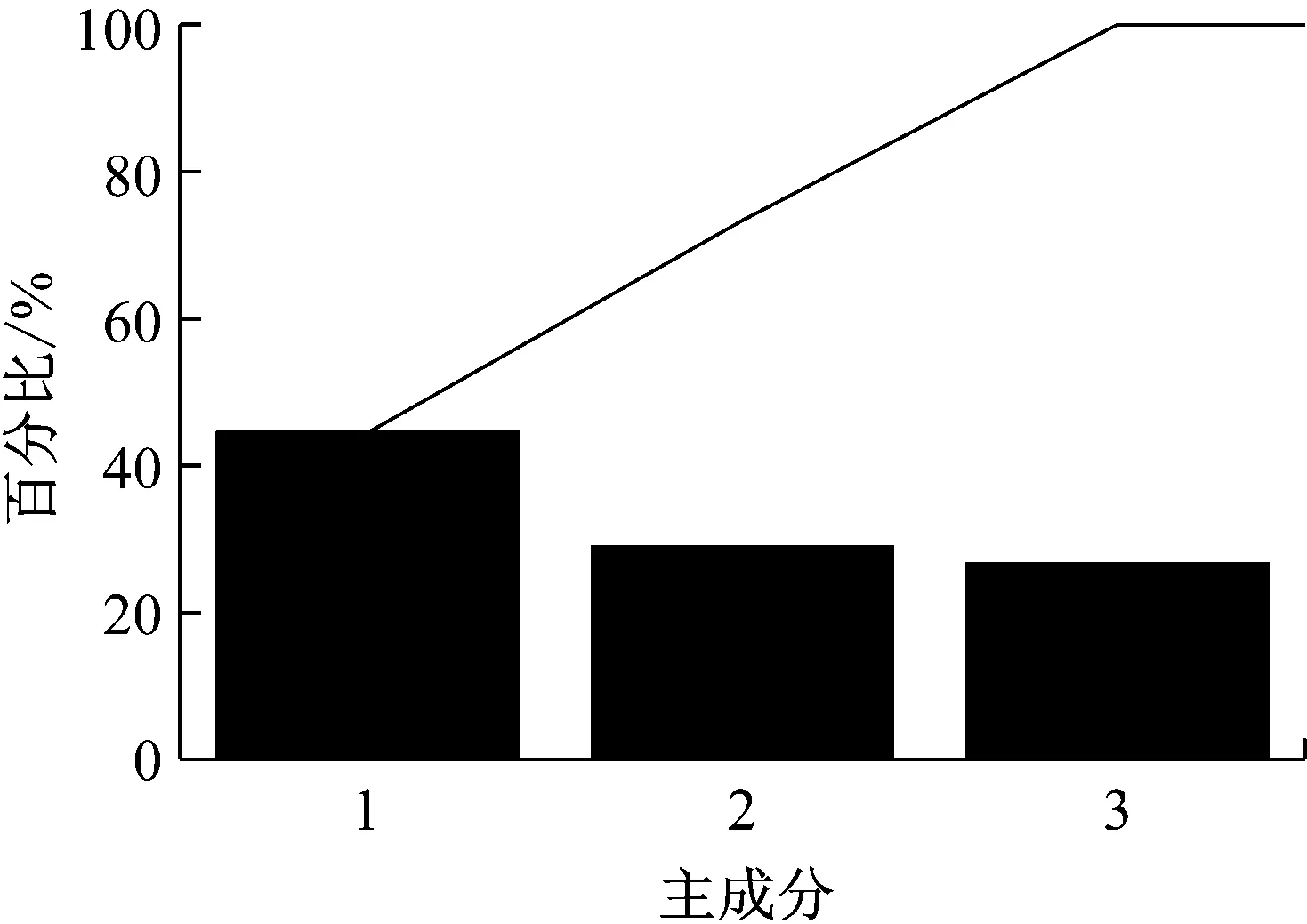
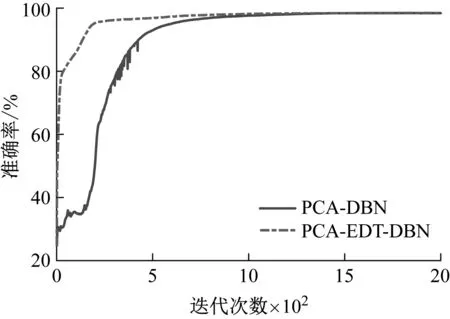
设样本输入数据维度为D,即输入层单元数为D,若2N-1 例如,DBN的输入数据维度为784,29=512<784≤210=1 024,所以N=10。则5RBM(l=5)隐藏层单元数为u1=512,u2=512,512,512,512和u1=512,u2=256,u3=128,u4=64,u5=32。 (2) 批尺寸(batchsize) 批尺寸与训练样本数和测试样本数有关,本文设定为:如果训练样本数和测试样本数为S1和S2,则将批尺寸定为b1=100,b2=100和b1=S1/100,b2=S2/100,样本数若不是100的倍数则取接近值。 对于本文的数据应用,此处采用两种计算组合来举例说明,一是隐藏层数l=2、隐藏层节点数u1=1 024,u2=512和批尺寸b1=99,b2=99,二是隐藏层数l=3、隐藏层节点数u1=1 024,u2=512,u3=256和批尺寸b1=99,b2=99。RBM的参数设置为:将可视层与隐藏层偏置以及学习率初始值均设为0.1,初始动量设为0.5,迭代5次后,动量变为0.9。为了消除算法随机性,每次实验都重复10次,取10次结果的平均值。结果如图4所示。 图4 原始数据-DBN诊断结果 从图中结果可以看出,对于行星齿轮箱齿面磨损故障而言,利用原始振动数据进行诊断的准确率只有25%左右。此外,由于输入数据维度太大导致模型训练时间特别长,两个模型的平均训练及测试时间分别为1.315 6×104s和1.399 3×104s。 由于每种故障都有其独特的特征频率,所以利用FFT将信号从时域转换至频域可以更好地反应各故障的自身特征,利于故障诊断。基于FFT的DBN诊断方法是在上节数据基础上,将数据从时域转换至频域,从而使输入数据维度从2 000降至1 000。在计算过程中,除各隐藏层单元数都对应降低一半之外,其余参数设置不变,对上述数据分析结果如图5所示。从图中结果可以看出,相对于原始时域信号作为输入的情况,经过FFT变换至频域信号作为输入时诊断准确率明显提高,迅速收敛且结果稳定,说明频域信号代表的故障特征信息更准确、更适用于该模型。此外,训练时间也大幅减少,基本在10 min左右,可以说效果很好,接下来的研究主要看是否可以进一步缩短计算时间。 图5 FFT-DBN诊断结果 特征参数指表征物质或现象特性的参数信息,对传统的智能故障诊断方法十分重要,特征参数提取和选择的好坏关系着诊断准确率的高低。本文利用振动信号特征参数作为DBN输入对上述数据进行诊断,提取了36个参数,见表1[13-14]。 表1 特征参数 模型参数设置以隐藏层数l=2为例,隐藏层节点数u1=32,u2=16,其它设置与前文相同,结果如图6所示。从图中结果可以看出,基于特征参数的DBN故障诊断方法准确率很高,约为98%,在迭代500次之后基本达到稳定。此外,模型训练时间也大幅减少,基本在75 s左右。但是该方法前期的特征提取工作需要一定的专业性,需要花费一定的时间和人力。 图6 特征参数-DBN诊断结果 综上三种传统的DBN故障诊断方法结果可以看出,采用原始数据直接作为模型输入时,结果准确率低,训练时间长;采用FFT变换后的信号作为模型输入时,准确率提高了很多,训练时间也相应减少,但仍然可以进一步降低;采用特征参数作为模型输入时,准确率很高,训练时间也很短,但是对专业性有一定要求。 针对上节基于DBN的传统故障诊断方法存在诊断准确率低、训练时间长和专业性要求高等问题,本节对本文提出的基于PCA-EDT-DBN的故障诊断方法进行研究。首先给出方法流程,然后利用与之前同样的数据进行分析来验证方法的有效性。 由于PCA和EDT都是比较成熟的技术,篇幅有限,本文不再对其理论进行赘述,可参考文献[15-16]。 本文提出的基于PCA-EDT-DBN的行星齿轮箱故障诊断方法流程如图7所示,具体步骤如下: (1) 设备运转振动数据采集;在此步骤中需要设置多个传感器同时采集信号以提高诊断精度,设采集到的数据样本为xn×m,其中m为传感器个数,n为每个传感器采集到的数据点数。 (2) PCA数据降维;运用PCA方法分别对各个传感器数据进行分析,根据需求取前p个主成分(通常占总成分的95%),得到PCA结果矩阵ym×p。 图7 基于PCA-EDT-DBN的故障诊断方法流程 Fig.7 The flowchart of the fault diagnosis method based on PCA-EDT-DBN (3) 一维向量生成;一维向量由两部分组成:第一部分是计算ym×p每两列之间的欧氏距离,得到距离矩阵Dp×p,将矩阵中各向量自身与自身距离结果(0)去掉后按序展开得到一维向量d1×p(p-1);第二部分是将矩阵ym×p按列的顺序展开成一维向量z1×mp;将两部分组合得到最终的一维向量f1×(mp+p(p-1))=[z1×mp,d1×p(p-1)]。 (4) DBN诊断结果输出;利用训练数据训练DBN,然后利用测试数据测试DBN效果给出诊断结果。在此步骤过程中,本文提出基于正交试验设计的DBN参数优化方法来对DBN参数进行优化,结果更加理想。 数据构成及训练样本数和测试样本数与3上节相同,接下来用PCA方法处理每个样本,通过分析可知,4列信号中每列的前三个主成分即可达到占所有成分的95%以上,如图8所示。所以取p=3,即PCA结果矩阵大小为y4×3,展开成一维向量大小为z1×12。然后计算y4×3各列之间的欧式距离得到一个3×3矩阵,去掉矩阵中各向量自身与自身距离结果(0)展开成一维向量结果为d1×6。最后将z1×12和d1×6两部分组合得到最终的一维向量f1×18,即将样本维度由原本2 000维降至18维。 图8 主成分选取结果 处理好数据之后输入到DBN模型之中,首先设置模型参数。参照1.2节参数设定,选择隐藏层数l=3、隐藏层节点数u1=16,u2=16,u3=16和批尺寸b1=99,b2=99进行举例分析,其它各参数设置与前文相同。同时,为了证明EDT的有效性,对没有EDT过程的结果进行分析,即PCA-DBN方法,一维向量只为z1×12。此时的DBN参数设置为隐藏层数l=3、隐藏层节点数u1=8,u2=8,u3=8和批尺寸b1=99,b2=99,其它不变,得到结果如9所示。 在迭代2 000次之后两种计算结果都趋于稳定,此时PCA-EDT-DBN和PCA-DBN的诊断准确率分别为98.47%和98.42%,每次计算所用平均时间分别为181.157 4 s和173.861 8 s。虽然最后的准确率相差不大,但是由图中结果可知,PCA-EDT-DBN方法更稳定,在迭代次数或时间有限的情况下(如1 000次)效果更好。 图9 PCA-EDT-DBN和PCA-DBN诊断结果 Fig.9 The diagnosis results of PCA-EDT-DBN and PCA-DBN 此外,本文提出利用基于正交试验设计的DBN参数优化方法来优化DBN参数。依据1.2节设定,此处PCA-EDT-DBN方法的正交试验因子与水平为: A:隐藏层数(l):l1=2,l2=3,l3=4,l4=5; B:隐藏层单元数(u):u1=16,u2=16,…和u1=16,u2=8,u3=4,…; C:批尺寸(b):b1=99,b2=99和b1=144,b2=16。 因此,本文定义的正交试验设计属于混合水平,所用正交表为L8(4124)。 表2是得到的结果,从表中结果可以看出,1、2号试验准确率最高为98.94%,但是2号试验计算时间要少很多,所以2号试验(A1B2C2)比较理想。 表2 PCA-EDT-DBN正交试验结果与分析 在得到试验结果之后并不能依据当前最好结果确认第几号试验就是最优方案,因为从正交表中试验得到的最好水平组合,在全部试验中不一定是最优方案,可能通过分析得到的结果会找到更好的水平搭配。通常利用各因子在每一水平下结果的平均值m值和极差R来做进一步分析 mqi=∑y(Mi(qi))/qi (1) 式中:qi代表因子的水平数,i=1,2,…,r;y(Mi(qi))代表Mi因子第qi个水平所对应的结果。 极差(R)可以为各因子对最后结果的影响程度排序。一个因子的极差是该因子各水平下结果均值的最大值与最小值之差,用如下公式来计算: R=max{m1,…,mqi}-min{m1,…,mqi} (2) 进一步由m值分析之后可得,A1B2C1(隐藏层数l1=2,隐藏层单元数u1=16,u2=8,批尺寸b1=99,b2=99)组合可能准确率高且时间更短,进行试验得到结果为98.85%(115.104 8 s),综合考虑可能此组合更优。此外,对比R值可以发现,3个因子中A因子对准确率的影响最大,B和C因子对准确率影响不大,但是对计算时间影响很大,隐藏层单元数和批尺寸都呈现出总和越小计算时间越短的趋势。 在作者之前的研究成果中提出了基于EMD-EDT的特征提取及故障诊断方法,该方法对转速为1 200 r/min、负载为1.2 Nm工况下的太阳轮故障、行星轮故障、齿圈故障和正常状态四种状态信号故障诊断准确率为94.17%,可以说准确率也很高。但是该方法的应用涉及到很多具有专业性的信号处理技术,如TSA技术、特征提取及选择技术等,而且EMD计算时间很长。与之相比,本文提出的基于PCA-EDT-DBN的故障诊断方法的故障诊断准确率更高、计算时间更短,而且更加智能化,即使不具备相关领域知识也可以使用,是一种无监督的故障诊断方法。 此外,为证明DBN的有效性,利用与上述数据同样的训练样本训练BP神经网络然后用对应的测试样本测试诊断准确率,其中BP神经网络参数设置为:利用newff函数来创建BP神经网络,以训练数据来设定输入特征的范围,设定转移函数为“tansig”,在输出层选择线性函数“purelin”,训练函数选择“trainlm”,迭代次数设置为1 000,展示训练次数为10,误差允许值为1.0×10-10,学习率设置为0.01。训练时间用时113.024 1 s,准确率为为96.28%。虽然训练时间比本文提出的PCA-EDT-DBN故障诊断方法稍快,但是准确率低了两个百分点,还是可以证明DBN更有效。 本文针对基于传统DBN故障诊断方法在行星齿轮箱故障诊断应用上结果准确率低、波动性大、耗时耗力的问题,提出了基于PCA-EDT-DBN的行星齿轮箱故障诊断方法。分析了基于原始信号、FFT和特征参数的DBN故障诊断方法的性能,给出了基于PCA-EDT-DBN的故障诊断方法的方法框架。利用行星齿轮箱齿面磨损预置故障实验数据验证了本文提出方法综合性能要比传统的DBN故障诊断方法效果好,即该方法诊断准确率高、性能稳定、训练时间短、专业性要求低。此外,与BP神经网络对比证明了DBN方法的有效性。
1.3 基于FFT-DBN的诊断方法
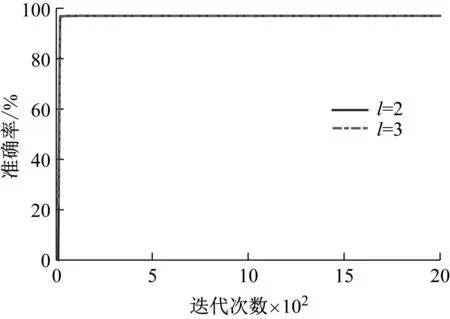
1.4 基于特征参数-DBN的诊断方法

2 基于PCA-EDT-DBN的诊断方法
2.1 方法流程

2.2 行星齿轮箱故障诊断
3 结 论
