基于试验验证的商用车驾驶室悬置参数优化研究

李 彬，曹 阳，运伟国

(1.长安大学 汽车学院，西安 710064； 2.吉林大学 交通学院，长春 130012； 3.浙江吉利新能源商用车集团有限公司,杭州 310052)

1 整车刚柔耦合多体动力学理论基础

根据ISO 2631—2003标准，车辆平顺性研究的主要频率范围为0.5～80 Hz,其中人体对0.5～12.5 Hz内的振动较为敏感。以往工程师在进行驾驶室悬置匹配与设计过程中，一般采用多刚体动力学的研究方法[9]。即将整车部件中除弹性、阻尼元件之外的其他部件均视为刚体，这种简化作为驾驶室悬置的初步选型在一定程度上是合理的，但是在实际车辆结构中，车架、车桥和车轮等主要零件均是具有弹性的[10]。根据商用车模态分布情况，对于全悬浮式驾驶室悬置结构，其刚体模态频率分布在1～8 Hz之间，发动机和车桥的模态在80 Hz之上，远远高于驾驶室悬置系统刚体模态频率，而车架的第一阶固有频率一般在10 Hz左右(与车架的长度有直接关系)，根据模态理论，任意激励的动态响应频率可视为系统各阶固有模态频率的线性组合，一般来说，固有模态频率与响应频率相隔越近则该阶模态对响应的贡献越大。因此可以判定发动机和车桥的弹性对整车平顺性的影响很小，而车架弹性的影响是较大的[11-13]。

在本文研究中，假设系统中车架、及驾驶室悬置支架为柔性体；驾驶室、驾驶员座椅、车桥等均为刚性体；悬架系统中的弹簧和阻尼力为力学单元，导向机构视为约束。

根据随机振动理论，一个具有m个输入Xi(t)(i=1,2,…,m)和n个输出Yk(t)(k=1,2,…,n)的常参数线性系统可用如图1所示的系统表示，其中Xi(ω)和Yk(ω)分别是Xi(t)和Yk(t)的傅里叶变换。Hki(ω)为第i个输入和第k个输出之间的频率响应函数。

经过傅里叶变换，并将输入输出写成矩阵形式，有：

X(ω)=[X1(ω)X2(ω) …Xm(ω)]T

(1)

Y(ω)=[Y1(ω)Y2(ω) …Yn(ω)]T

(2)

则系统的频率响应矩阵H(ω) 为

若设系统m个输入的自谱与互谱构成的m×n阶输入功率谱矩阵SX(ω)为：

n个输出的自谱与互谱构成的n×n阶输出功率谱矩阵SY(ω)为：

则输出功率谱与输入功率谱的关系可写成：

SY(ω)=H*(ω)SX(ω)HT(ω)

(3)

其中H*(ω)为H(ω)的共轭矩阵，HT(ω)为H(ω)的转置矩阵。

根据随机振动理论，设整车系统在l个车轮处激励相互独立，其相应的激励和功率谱分别为Xii(t)和Sii(f)(i=1,2,…，l) ，那么在仅考虑座椅处垂直方向加速度时其输出功率谱可表示为：

式中：Szz(f)为整车的输入功率谱矩阵，该矩阵为对角阵，可以表示为：

H(f)为系统的传递函数矩阵，可以表示为：

H(f)=[H1z(f)H2z(f) …H1l(f)]

(4)

相应的驾驶员座椅垂直方向加速度均方根值，表示为：

(5)

2 驾驶室悬置系统ADAMS建模与验证

2.1 刚柔耦合整车模型的建立

根据企业提供的CAD模型，应用多体动力学软件ADAMS/CAR 模块建立整车的虚拟样机，整车模型包括驾驶室及悬置系统、车架、前后悬架系统、前后桥等子系统。 首先建立车架、驾驶室、驾驶室悬置系统、前后悬架等的模板, 这其中包括构件的拓扑结构、运动副、衬套以及输入、输出通讯器；其次，根据模板建立子系统；最后由各个子系统组装成整车模型。整车各硬点坐标均来自CAD模型，对关键硬点相对位置进行了实车测量校核。驾驶室质量参惯性参数及各级悬置、衬套的刚度及阻尼参数均来自于台架试验结果，驾驶室质量及转动惯量测试如图1所示，各参数见表1所示，虚拟样机如图2所示。

2.2 模型准确性验证

在进行整车模型的振动仿真分析之前，需要对整车模型进行验证及确认所建立模型的准确性，本次验证包括两个方面的内容：

图1 驾驶室质量及转动惯量测试

图2 刚柔耦合多体动力学Adams模型

表1 驾驶室质量参数

(1) 自由度与静平衡验证。该验证在模型建立完成后即可进行，目的是检验模型是否欠约束或是过约束。另外样机模型能否静平衡是能否顺利进行仿真计算的首要条件。系统静平衡的成功表明所建样机模型的约束和力学参数可以支撑起整车系统，从而保证整车系统正常的仿真计算。

(2) 载荷谱输入输出验证。本整车模型采用六立柱试验台进行驱动，通过试验台给汽车轴端加载位移信号，该位移信号是通过对试验采集的轴端振动加速度信号积分得到。同时获取模型中驾驶室座椅导轨位置的响应加速度与试验采集的相同位置的振动加速度进行对比，如果加速度均方根值误差控制在15%之内即认为模型准确，可以进行下一步的优化工作。通过该方法不仅可以验证模型的准确性还可以检验各级悬置及衬套刚度试验结果的准确性。

3 优化分析与结果

3.1 DOE优化试验设计

采用虚拟DOE正交试验技术对驾驶室悬置进行系统参数优化，以驾驶室悬置前后刚度，前后阻尼作为优化设计因数，K1为前悬置弹簧刚度；K2为后悬置弹簧刚度；C1为前悬置弹簧压缩阻尼；C2为后悬置弹簧压缩阻尼。每个因数分为三个水平。以驾驶员座椅导轨位置垂向加权加速度均方根值作为输出，计算影响驾驶员乘坐舒适性的每个因素的最佳水平。

表2 不同因素的水平值

优化时试验台的激励信号是选择车辆在B级路面上以70 km/h匀速行驶时通过测试得到的各轴头位移信号，该信号同样是通过对加速度信号积分得到的，并通过频谱分析进一步得到位移信号的自功率谱。

3.2 优化结果

经过仿真分析，对每种方案驾驶员座椅导轨位置的加速度均方根值进行计算，最终挑选出7种较为合理的组合方案，见表3所示。

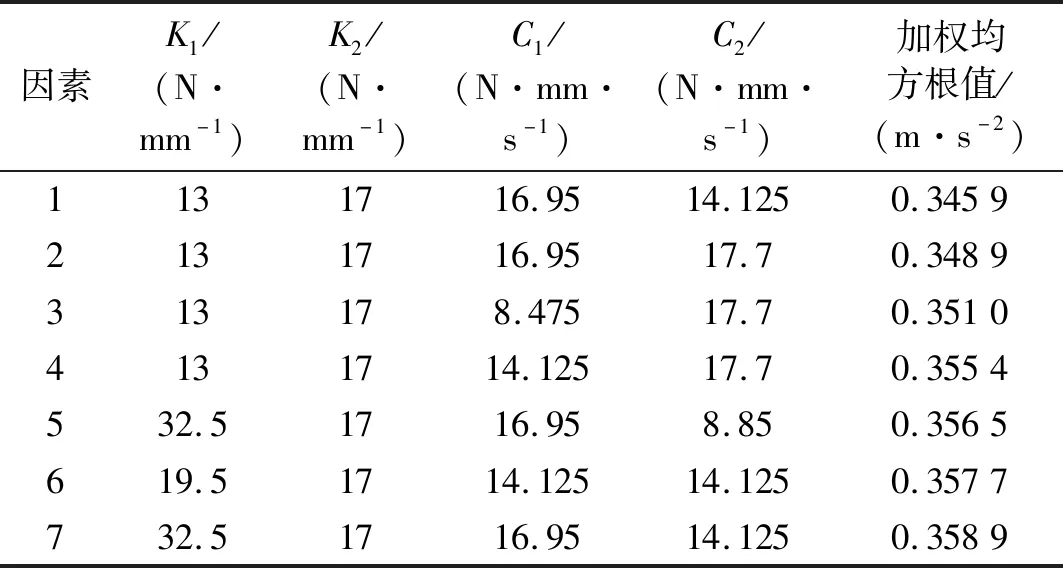
表3 优化结果

通过将上述7个方案分别在整车下通过虚拟B级路面进行路试。计算时分别以60 km/h、70 km/h、80 km/h的车速进行匀速直线行驶，检测驾驶员座椅导轨处加速度，并通过式(5)对加速度数据分别进行加权均方根值计算。7组方案中方案5、6、7对应的加权加速度均方根值较小。计算结果如表4所示。优化方案较原方案性能提升百分比见表5所示。

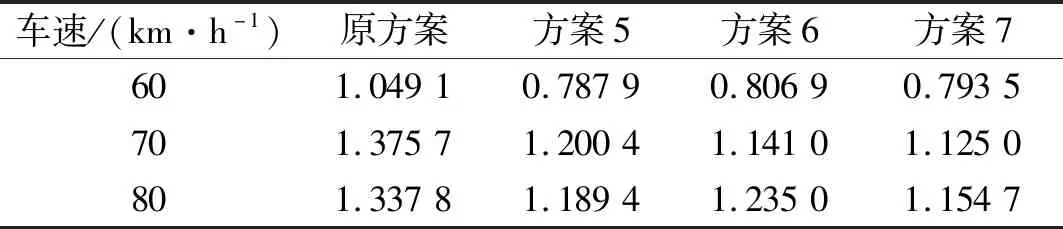
表4 三种较优方案计算结果

表5 三种较优方案性能提升率

根据以上分析方案7为最优方案，是考虑交互影响的前提下对垂直振动衰减最好的选择，使驾驶员座椅导轨处加权加速度均方根值改善了19%。

4 试验验证

按照上优化方案对车辆进行了改进，对改进后的车辆进行试验验证。根据ISO 2631—2003的规定，主要以驾驶室座椅导轨位置的加权加速度均方根值aw来评价平顺性。aw的计算公式为：

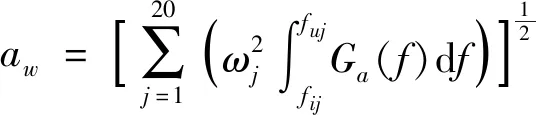
(6)

式中:fij、fuj分别为1/3倍频带的中心频带为fj的下、上限频率；Ga(f)为等带宽的加速度自功率谱密度；aω为单轴向加权加速度均方根值；ωj为第j个1/3倍频带的加权系数。

测试系统为LMS SCM09多通道振动测试系统，加速度传感器选择PCB ICP型加速度传感器，所用的Test.lab软件可以记录加速度时间历程，计算出测试过程中的aω，部分测试设备与传感器布置位置如图3所示。

(a) LMS数据采集仪

(b) PCB三向加速传感器

(c) LMS数据采集仪

(d) 传感器布置位置

本测试在西安绕城高速进行，测试工况均为匀速行驶工况，车速依次从40 km/h按照10 km/h递增至80 km/h，测试结果如图4所示。

图4 改进前后驾驶员座椅导轨处加速度均方根值对比

Fig.4 Comparison of the root mean square value vibration acceptation of driver seat rails before and after improvement

从图4得知，优化后的驾驶室悬置对在各车速下整车平顺性均有所提升，平均提升9.6%。其中，60 km/h到70 km/h车速时加权加速度均方根值下降，主要原因是60 km/h时轮胎不平衡引起的一阶激励与驾驶室刚体模态重复。由于试验道路与仿真所加载的B级路面激励的不一致，其优化提升幅度低于仿真结果，但在一定程度上证明了仿真优化的有效性和科学性。

5 结 论

(1) 以多体系统动力学理论为基础，以机械动力学仿真软件ADAMS为工具，建立了基于整车的全浮式驾驶室悬置系统刚柔耦合的参数化仿真模型，利用DOE试验方法以驾驶员座椅导轨位置的加速度均方根值为目标进行了优化。通过实车道路试验证明优化后整车行驶平顺性较优化前提升了9.6%，说明该优化方案是正确的，科学的。

(2) 改优化方案充分考虑了车架刚度及驾驶室悬置支架刚度等对驾驶室悬置匹配的影响，把其作为弹性体建模，该方法可以作为车架等刚度设计目标的制定依据，另外还可以利用该模型对车架刚度，驾驶室悬置支架刚度对车辆平顺性的影响进行研究。