2×1 500 m双主跨斜拉桥静风失稳机理研究

胡传新，周志勇，闫康健

(1.同济大学 土木工程防灾国家重点实验室，上海 200092； 2.同济大学 建筑设计研究院(集团)有限公司，上海 200092)

大跨度斜拉桥在静风荷载作用下，主梁发生弯曲和扭转变形。当来流风速超过临界风速时，随着结构变形的增大，结构抗力的增加速度小于静风荷载增加速度，此时结构发生静风失稳[1]。尽管国内外迄今为止未发生大跨度桥梁的静风失稳现象，然而随着跨径的不断增加，向着更长、更大、更柔方向发展，越来越多的学者在风洞试验中观测了大跨度桥梁静风失稳现象。大跨度桥梁静风稳定问题正在成为制约大跨度桥梁跨径进一步突破的核心和关键问题。

以往研究普遍认为大跨度桥梁的静风失稳风速高于颤振临界风速。然而，最新研究表明，对于跨度超千米级的超大跨径桥梁，随着跨径增大，结构刚度不断降低，静风失稳与颤振失稳存在着竞争关系，静风失稳可能先于颤振失稳发生[2]。Hirai等[3]最早在悬索桥的全桥气弹模型中发现了明显的静风失稳现象。之后，同济大学风洞实验室[4-5]在对汕头海湾二桥(主跨518 m，斜拉桥)、西堠门大桥(主跨1 650 m，悬索桥)和主跨1 400 m单箱梁斜拉桥方案的全桥气弹模型风洞试验中均发现了静风失稳现象。静风稳定性是千米级斜拉桥抗风性能的主要考验之一。而根据文献[6]确定的静风发散临界风速误差较大。因此，深入研究千米级桥梁的静风稳定性显得尤为重要。

目前，大跨桥梁三维非线性静风稳定性分析方法已经较为成熟[7-10]。诸多学者结合工程实例，对不同结构体系的大跨度斜拉桥进行了静风稳定参数敏感分析。程进等[11]以主跨为1 000 m的双塔双索面斜拉桥结构体系为研究对象，研究了初始风攻角、桥塔风荷载、拉索风荷载、桥塔高度、边跨跨径对结构静风稳定的影响，同时还比较了南京二桥、汕头海湾二桥和荆沙桥主梁断面对结构静风稳定的影响。李加武等[12]研究了初始风攻角、桥塔风荷载、拉索风荷载和边跨风荷载对主跨1 200 m双塔双索面斜拉桥静风稳定性的影响。张志田等[13]和张文明等[14]研究了紊流对大跨度桥梁静风稳定的影响。此外，一些学者还对双主跨三塔悬索桥静风失稳形态[15-16]，以及考虑风速空间分布特性的静风稳定特性[17]进行了较为深入的研究。研究发现，双主跨悬索桥的中塔和两侧主缆的协同作用明显，导致双主跨三塔与单主跨双塔悬索桥静风失稳形态明显不同。与双塔斜拉桥相比，三塔斜拉桥由于中塔缺少端锚索和辅助墩等约束，整体刚度更低，风作用下结构的稳定性问题更为突出[18]。韩大建等[19]对主梁为开槽断面的三塔双主跨斜拉桥香港汀九桥(127 m+448 m+475 m+127 m)进行了非线性静风稳定分析。李渊等[20]采用非线性空气静力稳定性分析方法，对主梁为开口断面的三塔双主跨斜拉桥-武汉二七长江大桥(主跨616 m)进行了分析，发现不同初始风攻角下，结构失稳形态不同，0°初始风攻角下，静风最大位移发生在距离中塔约1/4倍单主跨长度，还探讨了初始风攻角、中塔刚度及辅助墩对静风失稳的影响，并从风荷载与结构抗力的关系的角度对不同初始攻角下结构静力失稳机理进行了定性解释。然而，上述研究仅仅依据失稳过程结构位移响应演变特性揣测结构刚度的变化，并未指出引起结构刚度变化的深层次原因。此外，上述研究均未考虑拉索分段的影响，数值计算结果也未得到风洞试验验证，对于双主跨三塔大跨度斜拉桥静风失稳内在机理尚不明确。

由上可知，尽管目前对大跨度斜拉桥静风稳定性有了一定的认识，但存在诸多不足：研究对象主要针对双塔斜拉桥，很少涉及三塔斜拉桥，对三塔斜拉桥静风稳定性研究尚不充分；研究大多均为数值方法，没有经过风洞试验验证，特别是双主跨三塔大跨度斜拉桥静风失稳现象尚未有报告。以琼州海峡大桥论证方案主跨2×1 500 m三塔两跨斜拉桥结构体系为研究对象，采用全桥气弹模型风洞试验与数值计算相结合的方法，对失稳过程中结构位移响应和拉索索力进行跟踪，从失稳过程结构刚度演变特性角度揭示了双主跨三塔大跨度斜拉桥静风失稳机理。主要研究内容：全桥气弹模型风洞试验研究，分析失稳现象，并提取了失稳过程结构主梁位移响应演变特性；基于ANSYS10.0有限元软件，考虑结构几何非线性及静风荷载非线性，采用增量与内外两重迭代相结合的非线性静风稳定分析方法进行了优化迭代分析[12]，提取了失稳过程结构主梁位移响应及与之同步的拉索索力演变特性；风洞试验与数值计算结果进行对比分析验证数值算法的可靠性；对失稳过程与结构响应同步的结构刚度演变特性及失稳形态进行分析，揭示了双主跨三塔大跨度斜拉桥静风失稳内在机理。

1 试验概况

1.1 结构体系

2×1 500 m三塔两跨空间双索面斜拉桥桥跨布置为(652+1 500+1 500+652)=4 304 m。主桥桥面纵坡采用1.0%，主梁断面为分离双箱断面。其中，梁宽B为60.5 m，中心线处梁高H为5 m，开槽率为23%。结构总体布置及主梁断面分别见图1和图2。主梁截面单箱竖向惯性矩、扭转惯性矩和扭转转动惯量分别为3.266 4 m4、50.994 m4和7.516 7 m4，弹性模量为2.10×1011Pa。

图1 桥型布置(m)

图2 主梁标准断面(m)

1.2 动力特性

2×1 500 m三塔两跨双索面斜拉桥结构动力特性分析采用通用有限元分析软件ANSYS进行，其中主梁、桥塔及桥墩采用空间梁单元模拟，拉索采用空间杆单元模拟，采用多段杆单元来模拟索曲线。主梁采用双主梁力学计算模型[21]，桥面系假设均匀分布于主梁上，并考虑其平动质量和质量惯矩。有限元模型见图3，自振频率见表1，一阶正对称竖弯和扭转振型如图4所示。

图3 有限元模型

1.3 试验概况

全桥气弹模型试验在同济大学土木工程防灾国家重点实验室TJ-3边界层风洞均匀流场中进行。该风洞是一个竖向布置的闭口回流式边界层风洞，试验段长14 m，矩形断面，断面宽15 m，高2 m。空风洞可控风速范围为1～17.6 m/s，连续可调，流场不均匀性指标δU/U≤1.9%紊流度Iu≤2.0%，来流竖向倾角Δα≤±0.2°，水平偏角Δβ≤±0.1°。气弹模型几何缩尺比为1∶320。主梁外衣采用豪适板模拟。桥塔外衣的材料均用有机玻璃板材经电脑雕刻后手工粘结而成，并在外侧粘贴雪弗板模拟外形。主梁和桥塔芯梁采用钢骨架。为了避免外衣刚度与钢骨架一起参与受力，外衣间隔分段，段与段之间留有1 mm左右的空隙。

表1 自振频率

(a) 一阶正对称竖弯

(b) 一阶正对称扭转

图4 振型

Fig.4 Shape diagram

气弹模型风洞试验主要测量对象为结构位移。风洞试验中的结构位移响应测量采用MEW-Matsuchita公司生产的MLS-LM10激光位移计，该位移计量程±50 mm，精度±0.02 mm。南侧桥梁主跨跨中和南侧桥梁主跨跨中和四分点位置和北侧主跨跨中位置各布置3个位移计，可同步测量主梁关键节点位置处主梁竖向、侧向和扭转位移。中桥塔和边桥塔塔顶分别设置1个顺桥向变形测点位移计和1个横桥向变形测点位移计，同时测量塔顶位置顺桥向、横桥向位移；共布置激光位移计16个，见图5所示。试验完成了图2所示主梁断面-3°、0°和+3°工况下的吹风试验，试验中通过在全桥气弹模型固定底板与风洞底板之间两侧插入一定厚度的铁块，改变模型姿态，进而实现+3°和-3°风攻角。模型实测动力特性如表2所示，除主梁一阶扭转外，其它阶模态频率误差均小于5%。

图5 全桥气弹模型

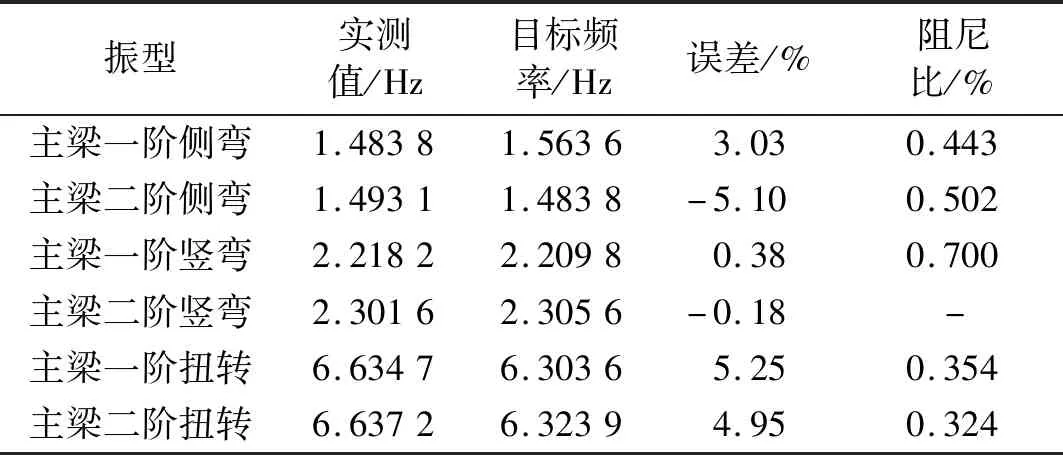
表2 实测动力特性

2 数值分析方法

2.1 静气动力参数

结构的静风失稳与静力三分力系数性质密切相关，且结构的失稳风速与升力矩曲线斜率成反比。风轴上的阻力系数CD、升力系数CL以及升力矩系数CM定义见式(1)，静力三分力方向如图6所示。其中，风轴上的阻力系数CD、升力系数CL，以及升力矩系数CM。定义如下：

(1a)

(1b)

(1c)

式中:CD(α)，CL(α)和CM(α)分别为风轴阻力系数、升力系数和升力矩系数；FD(α)，FL(α)和Mz(α)分别为风轴上阻力、升力和升力矩；U为来流平均风速；ρ为空气密度；B为主梁特征宽度，取值60.5 m；H为主梁特征高度，取值5.0 m。三分力系数基于风洞试验获得试验获得，见图7。

图6 气动力方向

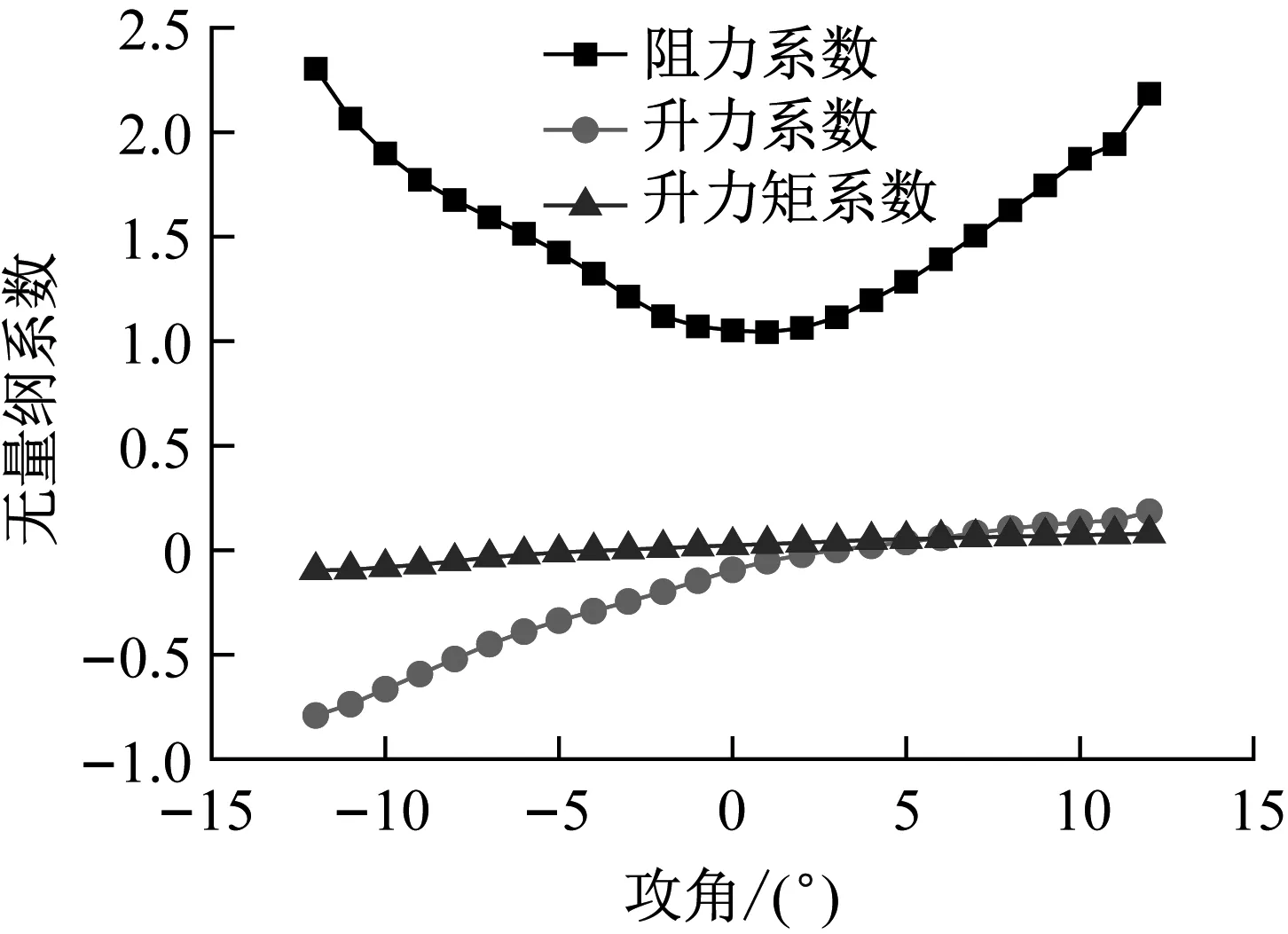
图7 静三分力系数

2.2 数值分析参数与方法

在确定静风失稳临界风速时，考虑结构几何及静风荷载非线性，忽略材料非线性对静风稳定的影响，采用增量和内外两重迭代相结合，并引入外层迭代次数上限的方法进行主桥结构的三维静风稳定分析。三分力系数由图7可得，超出-12°～+12°攻角范围时，进行多段线拟合外延获取三分力系数，忽略了三分力系数的雷诺数效应。基于主梁节段模型试验的静力三分力系数平均分配到双主梁上，实现了整体断面三分力与加载静风荷载的等效性。拉索阻力系数取1.2。采用多段杆单元模拟拉索并施加风荷载。以该结构初始风攻角0°为验算工况，计算了在110 m/s风速下拉索分不同段数所对应的跨中扭转位移和竖向位移，如图8所示。拉索分20段以上时误差已经很小，基本满足要求，故计算拉索分段取为20段。计算中采用主梁三分力的欧几里德范数是否小于收敛容差作为静力失稳与否的判断标准，不仅直观地反映了静风荷载的收敛情况，而且间接的反映了结构变形的收敛情况。文献[5]研究了收敛容差对1 400 m钢箱梁斜拉桥静力稳定性的影响，认为过大的收敛容差有可能导致过高估计桥梁整体静力稳定性，给抗风设计留下较大的安全隐患，是绝对不可取的。为了避免收敛容差可能带来的对静风稳定性分析的影响，以该结构(分离箱梁断面)初始风攻角0°为验算工况，计算了在110 m/s风速下收敛容差分别为 0.001、0.002 5、0.005、0.007 5、0.01对应的跨中扭转位移，如图9所示。当收敛容差小于等于0.005，扭转和竖向位移基本稳定，不再随收敛容差变化，故收敛容差取为0.002 5。

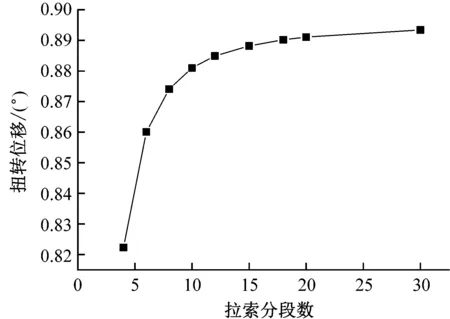
图8 主梁跨中位移随拉索分段变化

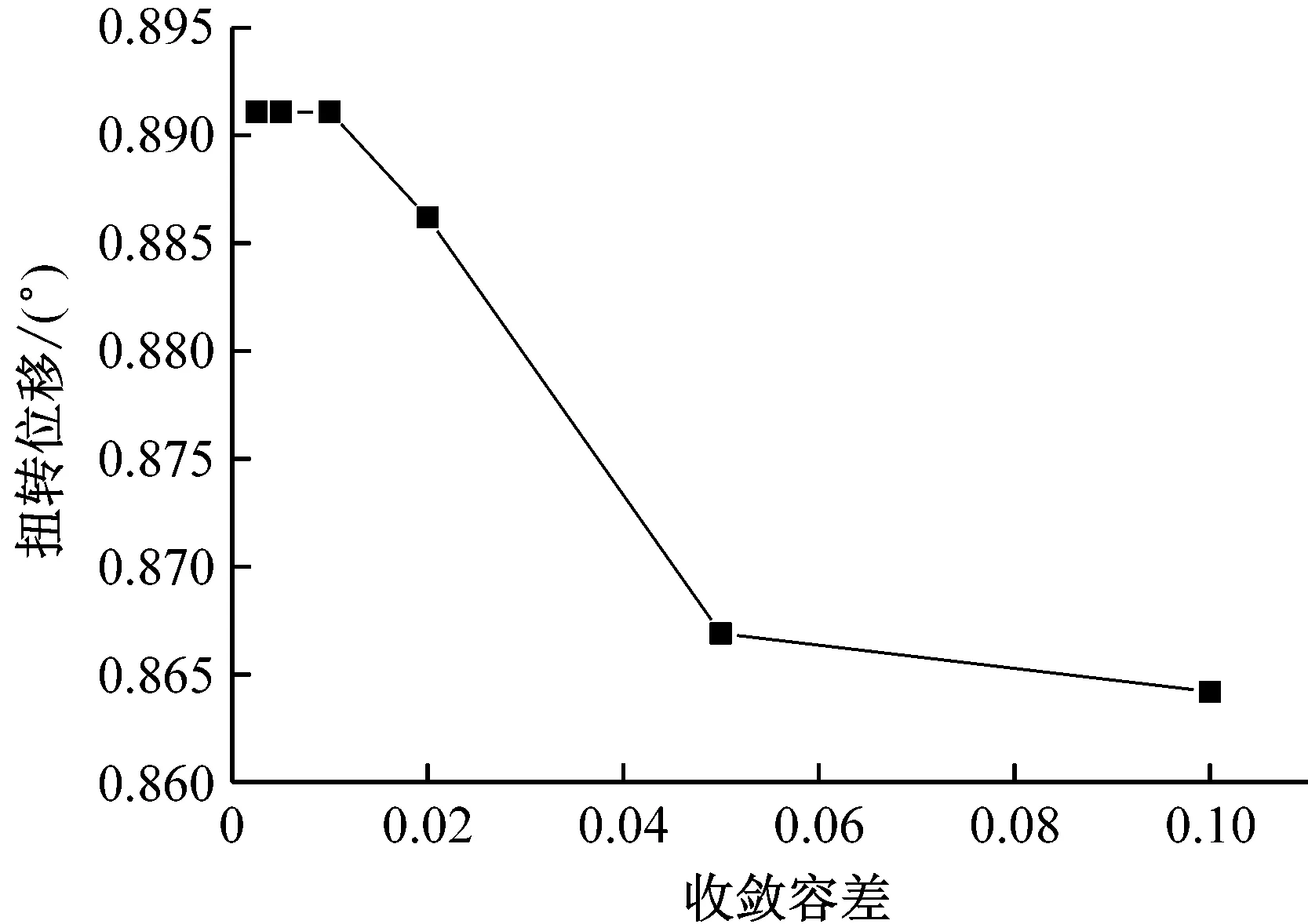
图9 主梁跨中位移随收敛容差变化

3 结果与分析

3.1 试验结果

试验风速为1.0～7.0 m/s，分别在-3°、0°和+3°初始风攻角下进行。全桥气弹模型试验中，在+3°和0°初始风攻角下均观测到明显的静风失稳前兆，图10显示了风洞试验中0°初始风攻角下处于即将静风失稳的气弹模型北侧跨中主梁状态。可知，此时结构具有较大的扭转变形，接近于静风失稳临界状态。图11给出了主梁跨中处扭转位移平均值及脉动值随风速的变化。随着风速的增大，扭转位移平均值及其斜率明显增大，即静风位移趋于发散；脉动值亦有增大，却无明显发散趋势。故综合实验现象及位移响应特性，可得到该结构在+3°和0°初始风攻角下的静风失稳临界风速估计值。初始风攻角为-3°时，在试验风速范围内没有观察到静风扭转位移发散现象。

图10 0°初始风攻角下静风失稳临界状态

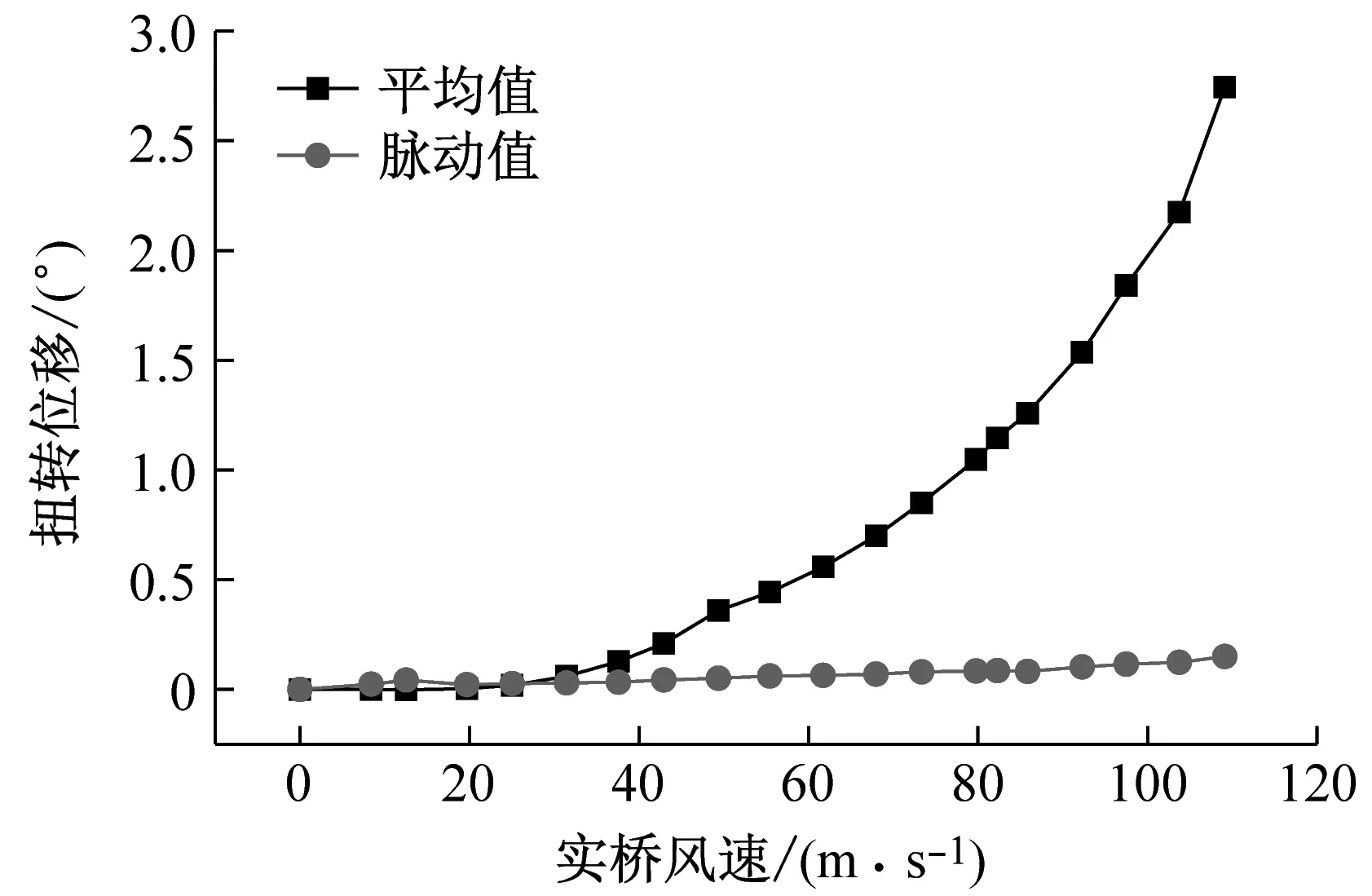
(a) +3°初始风攻角

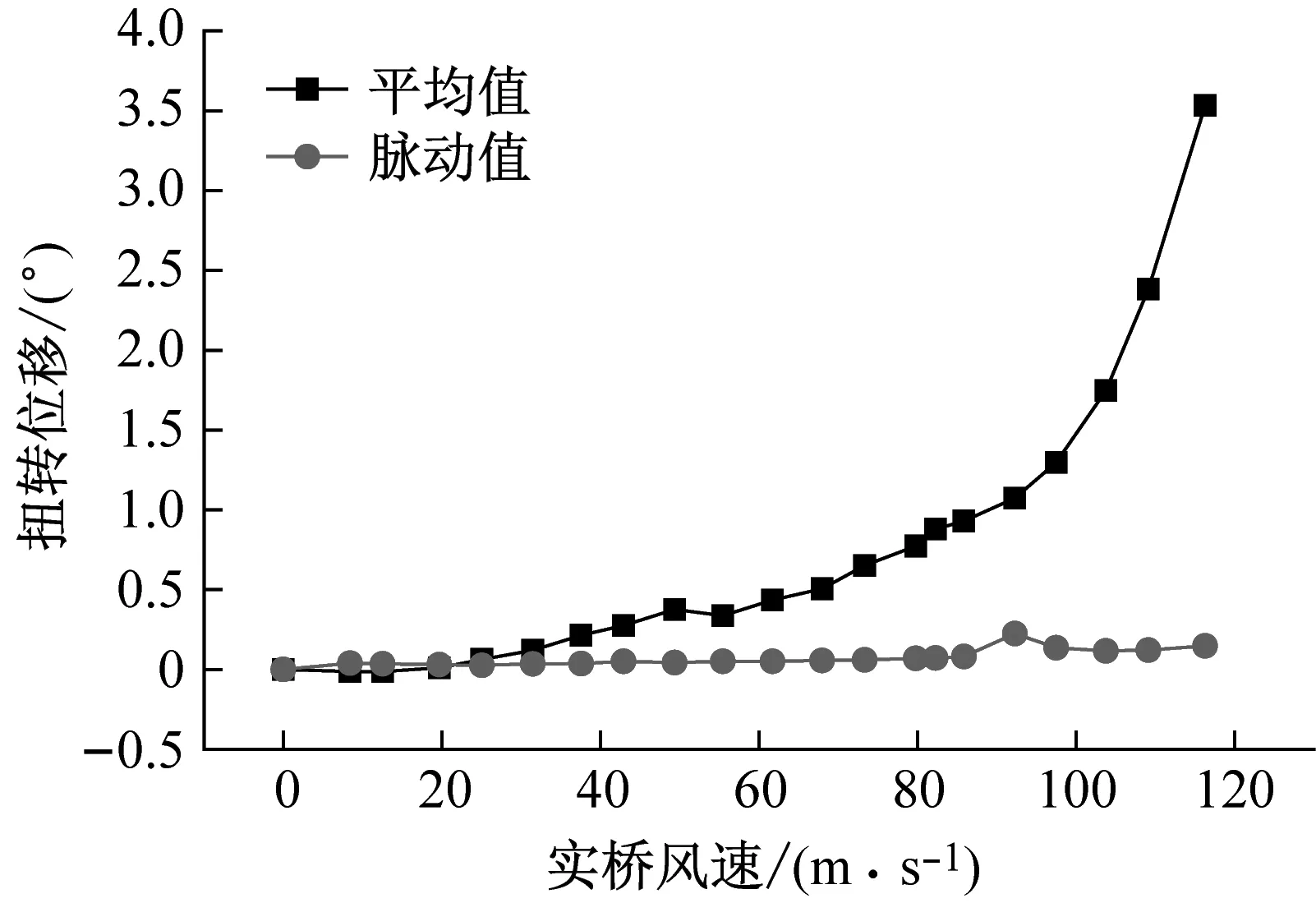
(b) 0°初始风攻角

为了进一步确定静风稳定与颤振稳定性关系，同时验证全桥气弹模型试验结果的可靠性，采用主梁节段模型试验，还对该主梁断面的颤振稳定性进行了验证。篇幅所限，不再赘述。零风速下，竖弯和扭转阻尼比分别为0.30%和0.18%。表3给出了基于全桥气弹模型试验的静风失稳临界风速和基于主梁节段模型的颤振临界风速。可知，+3°和0°初始攻角下，该结构的静风失稳先于颤振失稳。

3.2 试验与数值结果对比

表4给出了静风失稳临界风速的风洞试验值和计算值。其中，试验值为风洞试验中依据试验现象人为确定的临界风速。由于试验安全性的考虑，试验中未能施加更高试验风速，故表4中的试验值略小实际试验值。可知，试验值与计算值误差小于20%，吻合较好。图12给出了+3°和0°初始攻角下北侧跨中扭转及竖向位移-风速变化。可知，试验结果与数值计算获得的位移-风速变化趋势相近，二者较为吻合。故风洞试验值与计算值具有较好的一致性，也验证了本文数值模拟方法的可靠性。

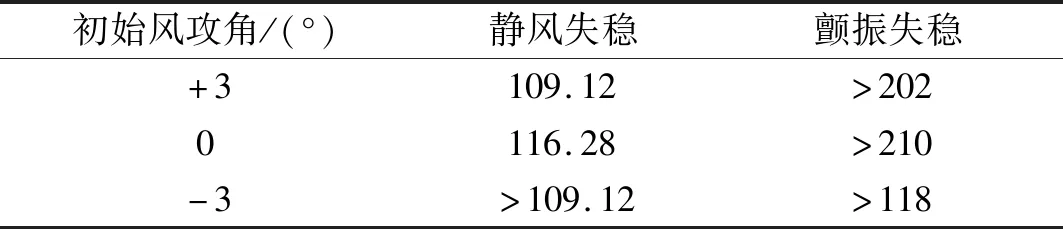
表3 失稳临界风速

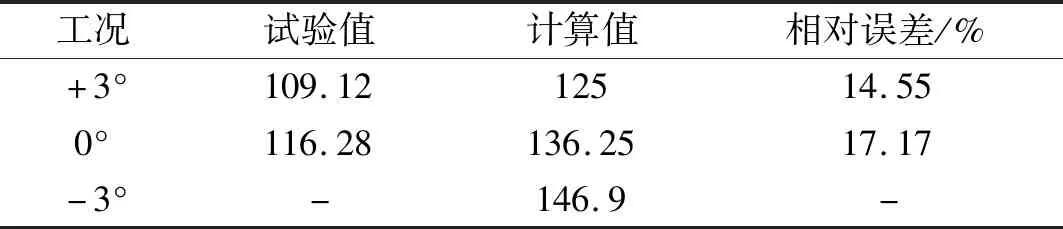
表4 静风失稳临界风速对比

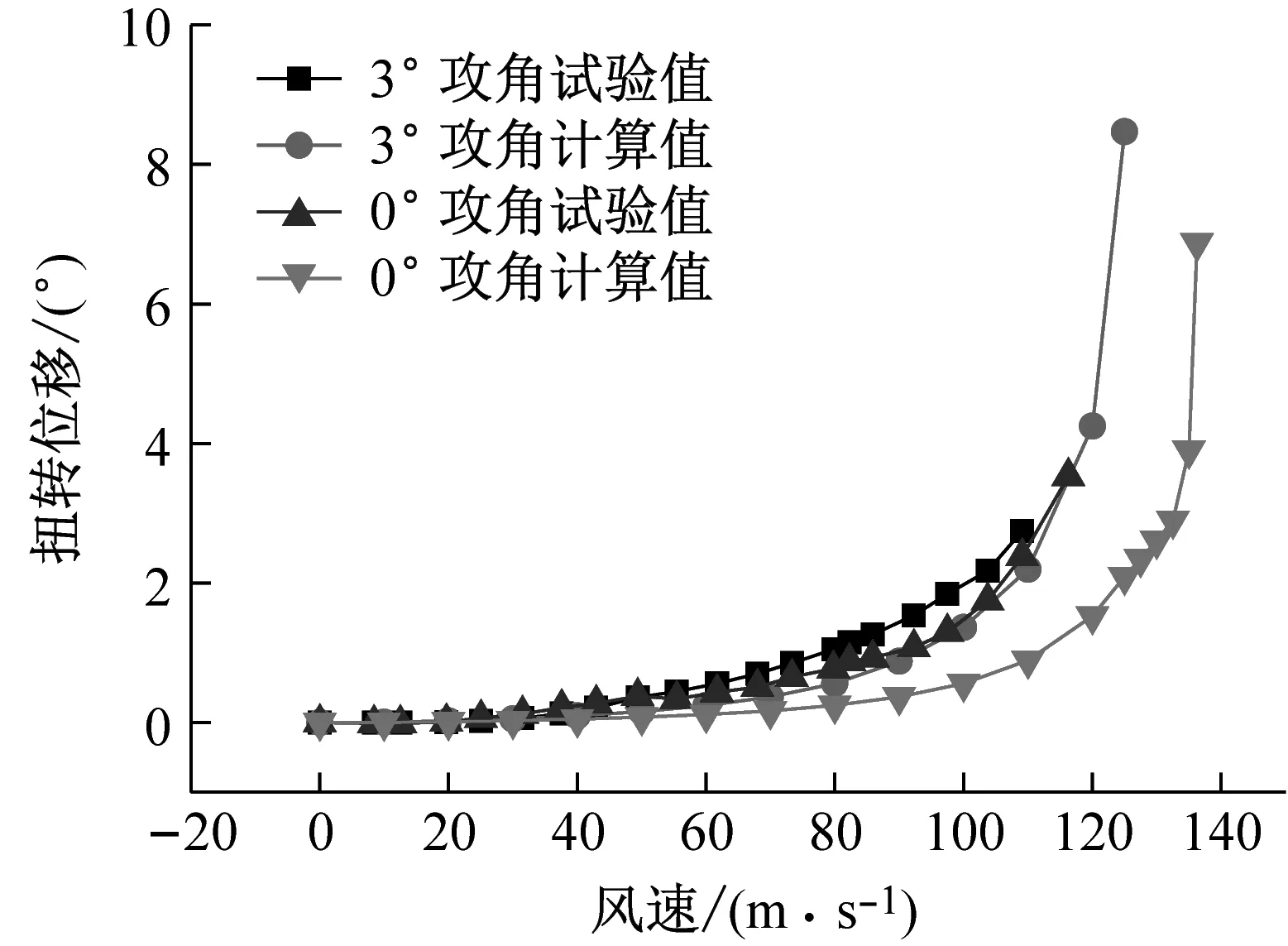
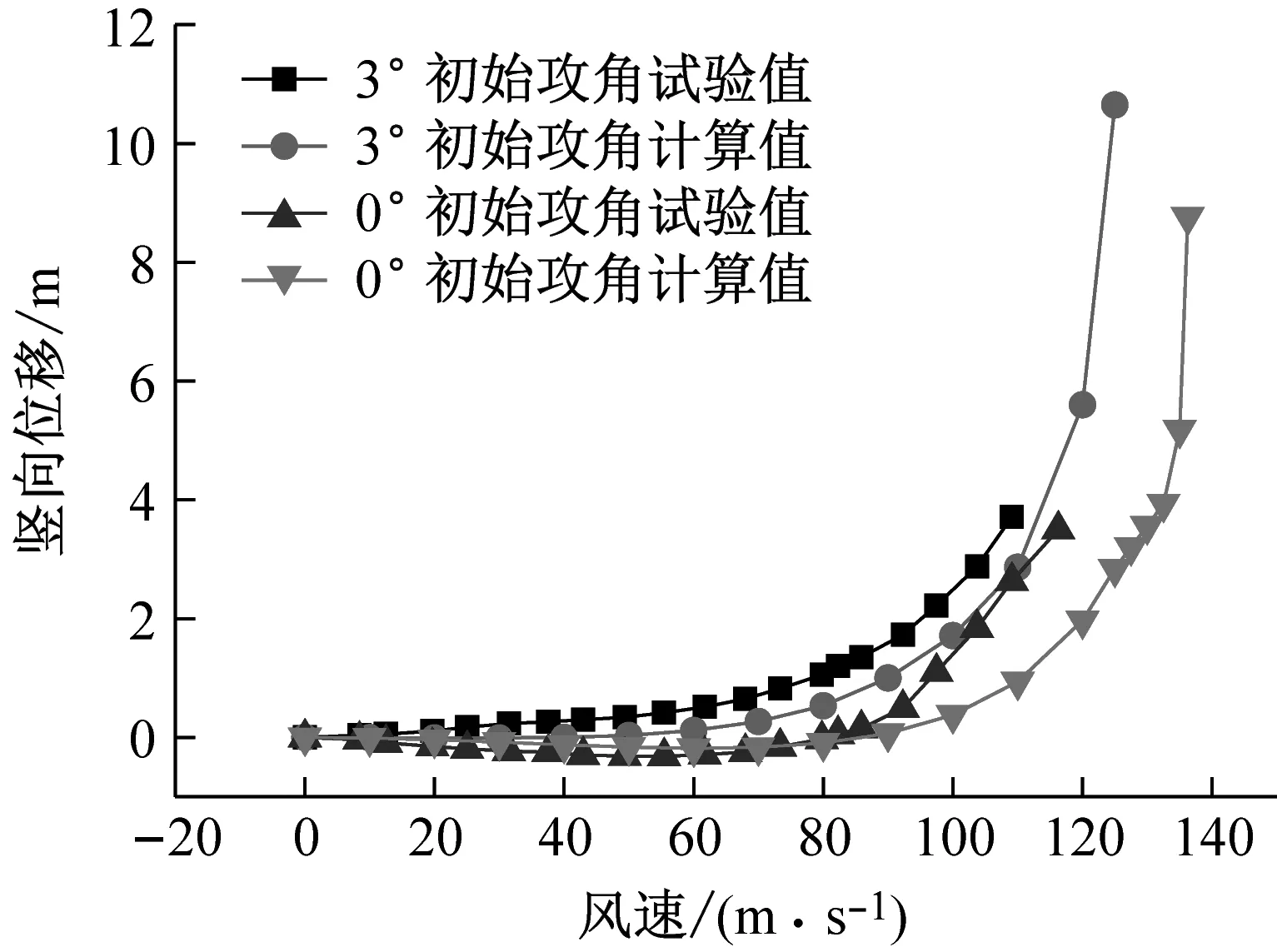
图12 数值模拟与试验结果的比较

3.3 失稳机理

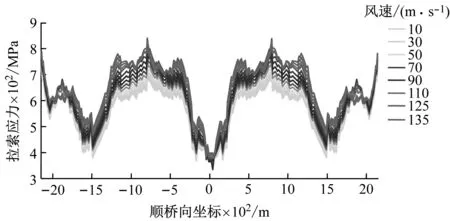
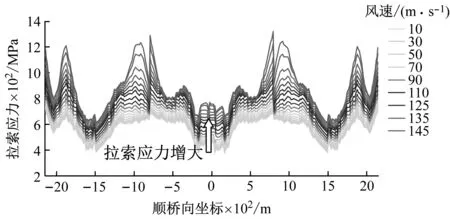
斜拉桥的结构刚度除主梁自身刚度外，拉索也是结构刚度的重要来源之一，主梁、两侧斜拉索和桥塔共同形成了空间稳定三角关系，提供了绝大部分结构刚度。针对+3°、0°和-3°三种不同的初始风攻角，追踪分析结构静风失稳全过程与结构响应同步的拉索索力变化，揭示失稳过程中结构刚度演化内在机制，以考察攻角效应对结构静风稳定性影响机理。+3°、0°和-3°初始风攻角下失稳过程拉索索力演变特性分别见图13～图15。图中，横坐标表示主梁上拉索锚固点的顺桥向坐标(以中塔轴线为坐标原点)，纵坐标表示相应拉索的轴向拉应力，不同颜色代表不同来流平均风速。可知，随着风速增大，上下游拉索在两主跨内对称变化，+3°和0°攻角时以跨中区域拉索最为明显，-3°攻角时跨中区域及靠近中塔四分点区域拉索尤为明显。为了展现失稳过程结构刚度与结构响应之间同步演变关系，选取跨中拉索进行分析。

+3°和0°初始攻角时，下游拉索索力在较低风速范围内随风速增大而增大，此时对结构刚度有强化作用，在风速为120 m/s时索力达到最大，之后迅速衰减直至失稳，索力对结构刚度的作用由强化转为失效，导致结构失稳。失稳过程中上下游拉索主梁锚固点处竖向位移向上，即主梁抬升，两侧拉索和主梁形成的稳定三角关系不断削弱。+3°初始攻角时，随着风速增加，上游拉索索力逐渐减小直至失稳，即失稳过程中上游拉索索力趋于失效。与+3°初始攻角有所不同，0°攻角时上游拉索索力在失稳过程中先增大后减小，即上游拉索索力对结构刚度的作用先强化后失效，提高了静风失稳风速，这也是0°初始攻角下静风失稳临界风速高于+3°时的根本原因。失稳过程中，上下游拉索主梁锚固点处竖向位移向先减小后增大，即主梁先下压后抬升，两侧拉索和主梁形成的稳定三角关系先加强后削弱。与+3°、0°初始攻角不同，-3°初始攻角时上下游拉索索力均随着风速的增大而增大，不断增大的拉索索力减缓了结构刚度下降速度，直至静风失稳。

(a) 上游拉索

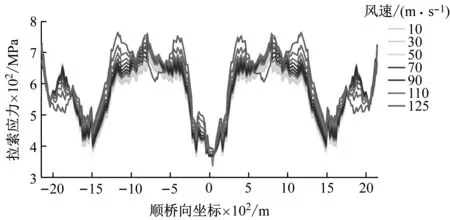
(b) 下游拉索

(a) 上游拉索

(b) 下游拉索

(a) 上游拉索

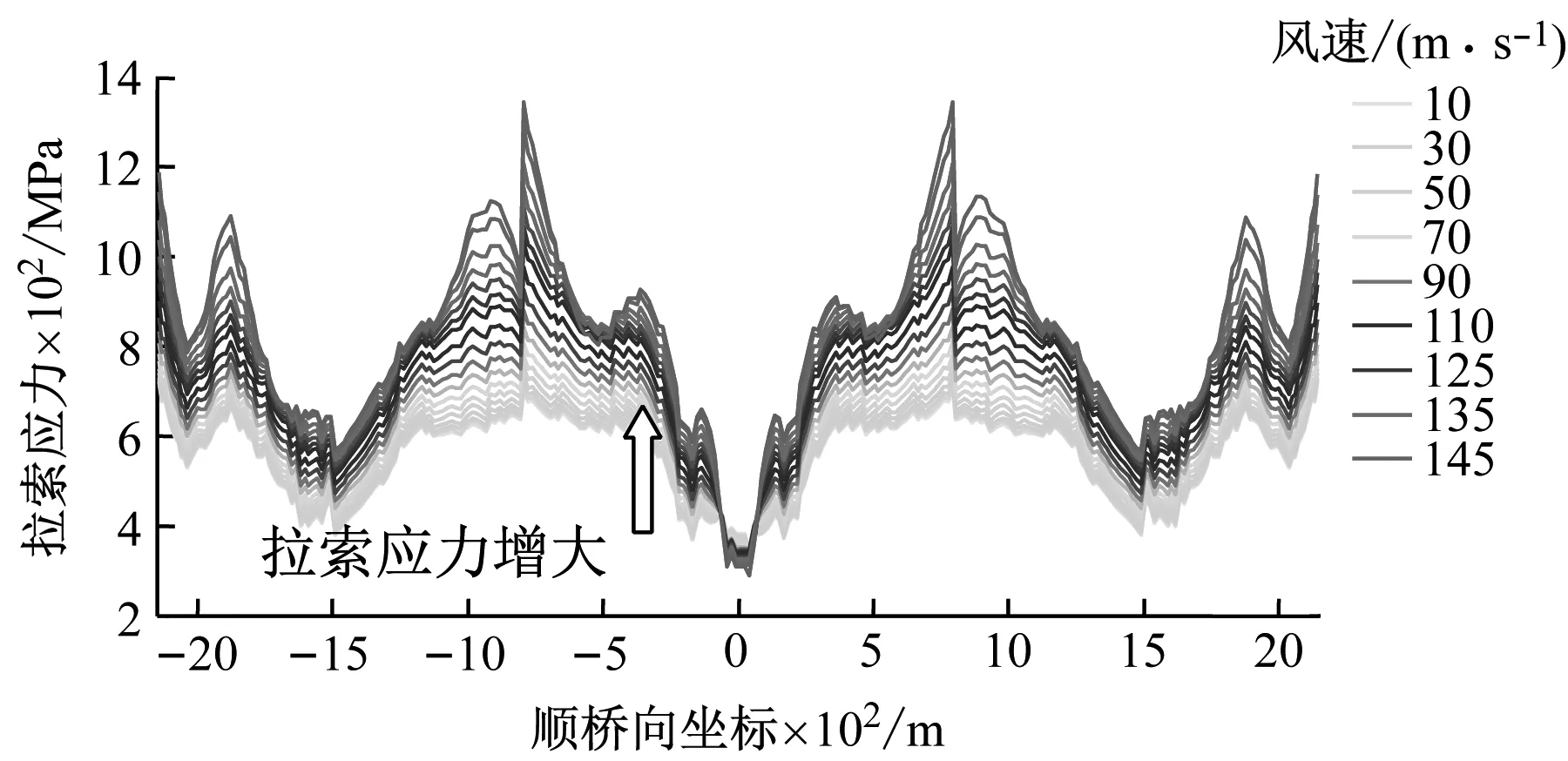
(b) 下游拉索

由上可知，最不利攻角为+3°风攻角，在该初始攻角下的静风失稳临界风速远小于-3°攻角。图16给出了失稳过程跨中拉索索力和主梁上拉索锚固点竖向位移演变特性。结合图16，分析其原因如下：加载后期，主梁断面在正攻角下产生整体向上的竖向位移，即主梁上抬，加速了拉索失效，从而破坏了两侧拉索和主梁形成的稳定三角关系，最终由主梁单独提供刚度，特别是扭转刚度，造成结构刚度急剧下降，因而结构迅速失稳；而主梁断面在-3°攻角下产生整体向下的竖向位移，即主梁下压，拉索索力不断增大，两侧拉索和主梁形成的稳定三角关系进一步强化，结构总体刚度下降较为缓慢，故失稳风速较高。

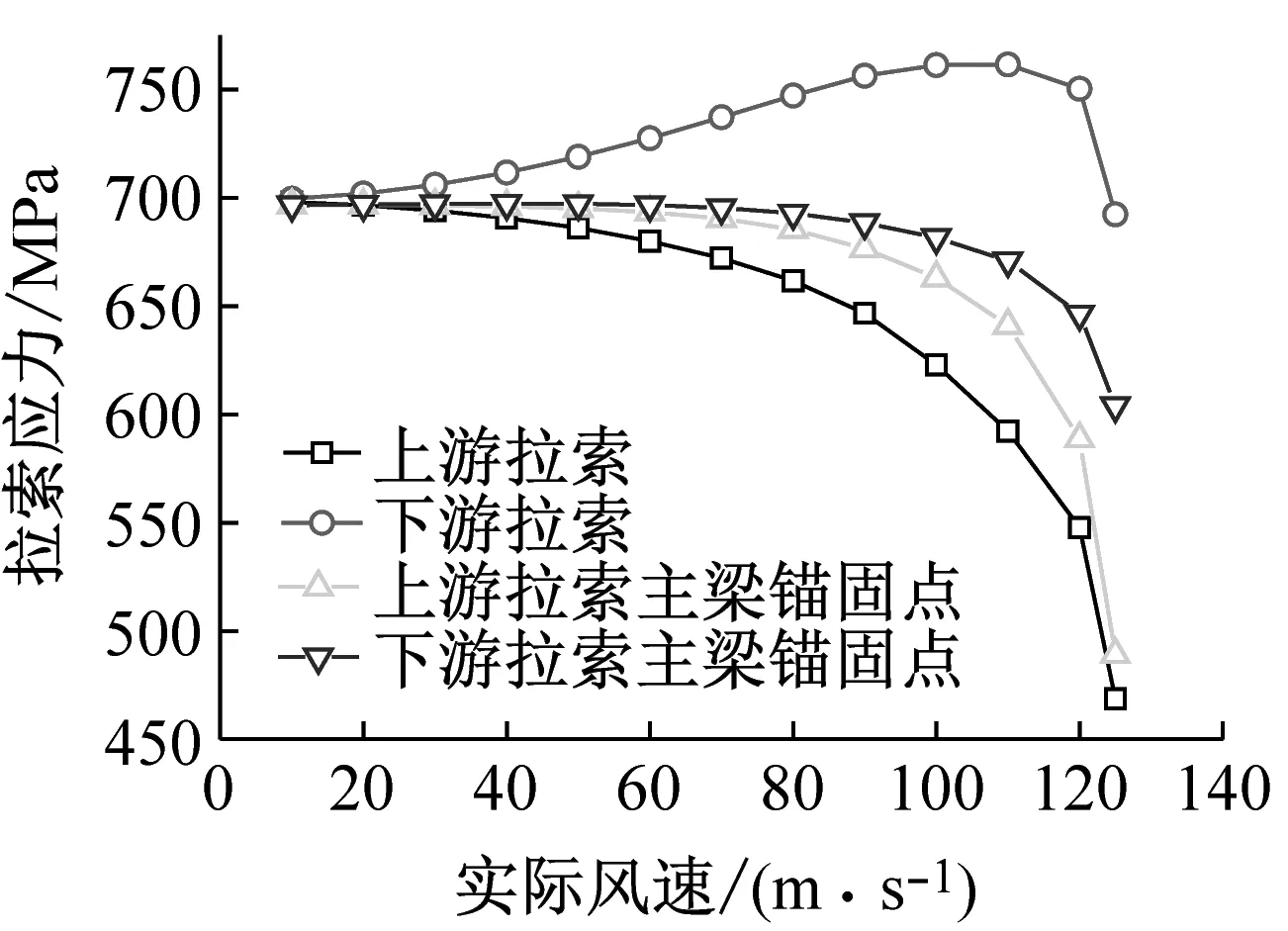
(a) +3°初始攻角

(b) 0°初始攻角

(c) -3°初始攻角

图17对比了不同初始攻角下失稳临界状态时结构扭转位移。+3°和0°初始攻角时，结构失稳形态关于中塔对称，即以主梁一阶正对称扭转振型失稳。-3°初始攻角时，结构失稳形态表现为明显的不对称形式，即以主梁一阶正对称扭转与主梁一阶反对称扭转耦合振型失稳，与结构对称的双塔单主跨斜拉桥明显不同。李渊等[20]也发现不同初始风攻角下，结构失稳形态不同。原因如下：由表1可知，结构的一阶正对称与一阶反对称扭转频率非常接近，误差小于1%。故从能量角度出发，激发结构反对称变形和对称变形所需的能量接近。故结构失稳表现为主梁一阶正对称扭转与主梁一阶反对称扭转耦合形式，且各振型参与度与失稳临界状态时主梁一阶正对称扭转与一阶反对称扭转频率的比值密切相关。

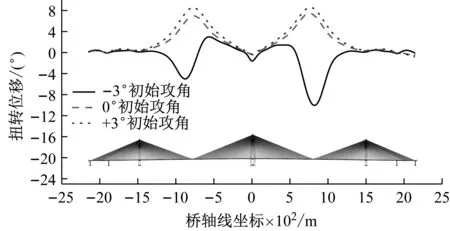
图17 结构失稳临界状态下扭转位移

4 结 论

以某主跨2×1 500 m三塔两跨斜拉桥结构体系为研究对象，采用全桥气弹模型风洞试验与数值计算相结合的方法，对失稳过程中结构位移响应和与之同步的拉索索力进行跟踪，从失稳过程结构刚度演变特性方面揭示了该结构体系静风失稳机理。

全桥气弹模型风洞试验发现：该结构体系在+3°和0°初始攻角下均出现了明显的静风失稳前兆，静风失稳先于颤振失稳发生，且+3°时失稳临界风速略低于0°。-3°初始攻角下的静风失稳临界风速远高于+3°和0°初始攻角。为了揭示上述现象发生的内在机理，提取与结构位移同步的拉索索力，对失稳过程结构刚度演变特性进行分析，研究表明：结构静风稳定性与失稳过程结构刚度演变特性密切相关，不同初始攻角下拉索索力演变特性的差异性引起静风稳定性能的差异。+3°初始攻角下，当风速较高时，主梁产生整体向上的竖向位移，加速拉索松弛，从而破坏了两侧拉索和主梁形成的稳定三角关系，最终由主梁单独提供刚度，特别是扭转刚度，造成结构刚度急剧下降，因而结构迅速失稳；而主梁断面在-3°攻角下产生整体向下的竖向位移，拉索索力不断增大，两侧拉索和主梁形成的稳定三角关系进一步强化，结构总体刚度下降较为缓慢，故失稳风速较+3°初始攻角高。-3°初始攻角时，结构失稳形态表现为明显的主梁一阶正对称扭转与主梁一阶反对称扭转耦合振型失稳，与结构对称的双塔单主跨斜拉桥明显不同。

研究首次在风洞试验中再现了双主跨大跨度斜拉桥静风失稳现象，揭示了大跨度斜拉桥静风失稳机理，为今后我国超大跨径斜拉桥的抗风设计具有借鉴意义。