涡轮增压器动力学建模及振动特性研究

顾灿松，袁兆成, 刘佳鑫，杨征睿，李洪亮

(1.吉林大学 汽车动态模拟国家重点实验室，长春 130025；2.中国汽车技术研究中心，天津 300162)

增压发动机以其高升功率、低排放以及低油耗等优点，一直受到市场的重点关注；随着政策法规对节能减排的要求越来越高，小排量、高效率发动机越来越受到市场的青睐；与之相对应的涡轮增压系统也逐渐成为汽油机的标准配置。涡轮增压器属于高速旋转机械，工作状态下其转子转速可达数十万转每分钟，因此对其可靠性及NVH性能都提出了很高的要求，高速下如何保证涡轮增压器的正常工作一直以来都是科研工作者的研究重点。

增压器转子实际上必然存在一定的偏心，当涡轮增压器高速运转时，会产生强烈的振动，并通过轴承及油膜传递至增压器壳体，影响涡轮增压器的工作性能及NVH水平。Mokhtar等[1-3]较早开辟了增压器转子动力学及油膜失稳机理等方面的相关理论与实验研究；Tanaka[4]和Li[5]率先应用轴承有限元模型预测油膜的稳态响应；Howard[6-7]在考虑了转子动力稳定性、负载及应力条件下，探究了涡轮增压器应用翼型轴承的可行性；Holt等[8-12]一直致力于结合轴承实际受力情形研究转子动力学模型，Holt等提出了一个完整的非线性转子动力学模型并全方位测量了高速运转的增压器壳体的振动加速度，编写了一个精确分析测出响应频率成分的非线性转子动力学程序。黄岩等[13-15]应用Black 模型和 Alford模型分别计算了密封结构、气流激振以及加速度对增压器转子动力学特性的影响。Gjika等重点关注浮环轴承涡轮增压器的非线性动力学模型，针对同步振动和转子总体振动的相关性进行分析。Andrés等采用仿真软件对涡轮增压器非线性转子动力学进行了计算，与实验结果高度吻合，为涡轮增压器的研究工作开辟了新的途径。

对于涡轮增压器的仿真计算，重中之重是对于浮环轴承模型的定义。浮环轴承是滑动轴承的一种，浮环与轴颈之间形成内油膜，与轴瓦之间形成外油膜，当转子旋转时带动浮环也一起转动，减小了与轴颈和轴瓦之间的相对速度，降低了摩擦功耗。国内学者对于浮环轴承的润滑特性研究较全面，彭立强等[16]和买吾拉·阿不都瓦克等[17]都应用了考虑热效应的热流体动力润滑模型，分别计算了内外层油膜间隙、浮环结构参数以及内外油膜压力和刚度对浮环轴承润滑特性的影响。李佳琪等[18-19]考虑浮环热弹变形建立了流体润滑计算模型，以研究浮环变形对于轴承润滑特性的影响，并探究了浮环内外层间隙、内外圆半径对浮环轴承润滑特性和环速比的影响。鉴于以上分析，本文首次采用柔性体多体动力学理论与EHD弹性液力润滑理论相结合的方法，对某汽油机涡轮增压器的振动特性进行了详细分析，得到了增压器浮环轴承的润滑特性以及增压器壳体和转子振动特性，为增压器NVH性能的研究与分析提供了新的思路。

1 多体动力学计算理论

1.1 雷诺方程表达式

浮环轴承具有功耗低、寿命长、结构紧凑等特点，是目前涡轮增压器常用的轴承结构形式。浮环轴承的浮环将轴承润滑油膜分为内外层两部分，在工作过程中，外层润滑油通过浮环油孔进入内层油膜，然后从两端流出，带走摩擦产生的热量，因此浮环轴承的雷诺方程表达式可分为内层油膜与外层油膜两部分。

根据广义不可压缩雷诺方程，浮环轴承内外层油膜雷诺表达式可做如下表述：

(1)

(2)

式中:RJ、Ri、Rk分别为轴颈、浮环内径、浮环外径，p是油膜压力，h为油膜厚度，UJ、UR分别是轴颈与浮环角速度，θ是角位移，η是润滑油动黏度。

1.2 油膜厚度表达式

在浮环轴承工作过程中，轴颈倾斜会导致油膜局部厚度变薄；同时在油膜压力作用下，轴颈、浮环以及增压器壳体会产生弹性变形，也会导致油膜厚度在实际工作时随载荷的变化不断变化。考虑轴颈倾斜、浮环以及增压器壳体弹性变形后油膜厚度方程如下描述：

(3)

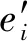
he=[K][P]

(4)

式中:[K]为变形矩阵，[P]为油膜压力，变形矩阵[K]可以通过有限元方法求解。

1.3 粗糙接触方程

在润滑油作用下，浮环轴承大部分时间内在液力润滑区内工作。但是在润滑条件不良、轴颈倾斜等特殊工况下，浮环轴承可能在混合摩擦区域内工作；混合摩擦是在轴承工作过程中比较常见，但是过大的混合摩擦区会增加轴承发热量、加速轴承磨损，甚至导致轴承烧结；因此在设计状态下对轴承的混合摩擦状态及混合摩擦区进行控制，以保证轴承正常工作。本文在混合摩擦区域引入Greenwood-Tripp理论来分析粗糙接触面的摩擦性能。粗糙接触面的摩擦产生的压力用以下公式描述：

(5)

(6)

式中:Pa为名义压力，ζ为粗糙度峰值的均方根，Rs粗糙面峰值半径，χs为接触面上粗糙峰值之和，δs为粗糙度，E*为粗糙面上的复合弹性模量，E*可做如下表述：

(7)

式中:E1,E2,ν1,ν2分别为接触对材料的弹性模量与波松比。

1.4 柔性体多体动力学方程

柔性体多体动力学方法考虑了结构件弹性对计算结果的影响，计算模型与实际模型更加贴近，计算精度也得到了很好的保证；该方法在运动件多体动力学特性的研究方面得到了广泛的应用。基于拉格朗日的柔性体多体动力学公式如下表述：

(8)

式中：ζ为柔性体广义坐标，M为柔性体质量矩阵，K为刚度矩阵，ψ为约束方程，为约束拉格朗日乘子，Δ为广义力。

将多体动力学公式(8)与公式(1)、(2)的雷诺方程联合求解，便可实现考虑轴承弹性液力润滑条件下的涡轮增压器的柔性体多体动力学计算。

2 涡轮增压器多体动力学建模

2.1 增压器子结构建模

有限元子结构建模基于模态综合法展开，模态综合法的基本思想是把复杂结构分成若干个子结构，用离散化方法对子结构做各种力学分析，得到各子结构的模态，然后通过坐标变换，得到用独立的各子结构模态坐标组成的描述整个系统运动的独立广义坐标。模态综合法能够大量降低计算模型的自由度，从而节约计算资源与计算时间。

图1所示增压器壳体、转子及浮环轴承装配示意图，图中可以看到，影响涡轮增压器多体动力学计算结果的结构主要有增压器壳体、涡轮转子、压气机转子及浮环轴承等；因此将以上结构视为弹性体，进行有限元建模。首先采用二阶四面体对涡轮增压器主要结构进行有限元划分,包括增压器壳体、浮环轴承和转子，有限元模型如图2所示。网格划分工作完成后，对增压器壳体和转子进行前处理。约束增压器壳体与发动机连接面，以模拟实际安装状态。同时，为便于EHD计算，保留转子与浮环轴承附近节点三向自由度，其中轴向保留5层节点，周向保留48个节点。以上设置完成后，开展有限元模型的模态缩减工作，得到用于多体动力学计算的质量矩阵与刚度矩阵，即为增压器多体动力学子结构模型。

图1 浮环轴承安装示意图

(a) 涡轮增压器转子有限元模型

(a) 涡轮增压器转子有限元模型

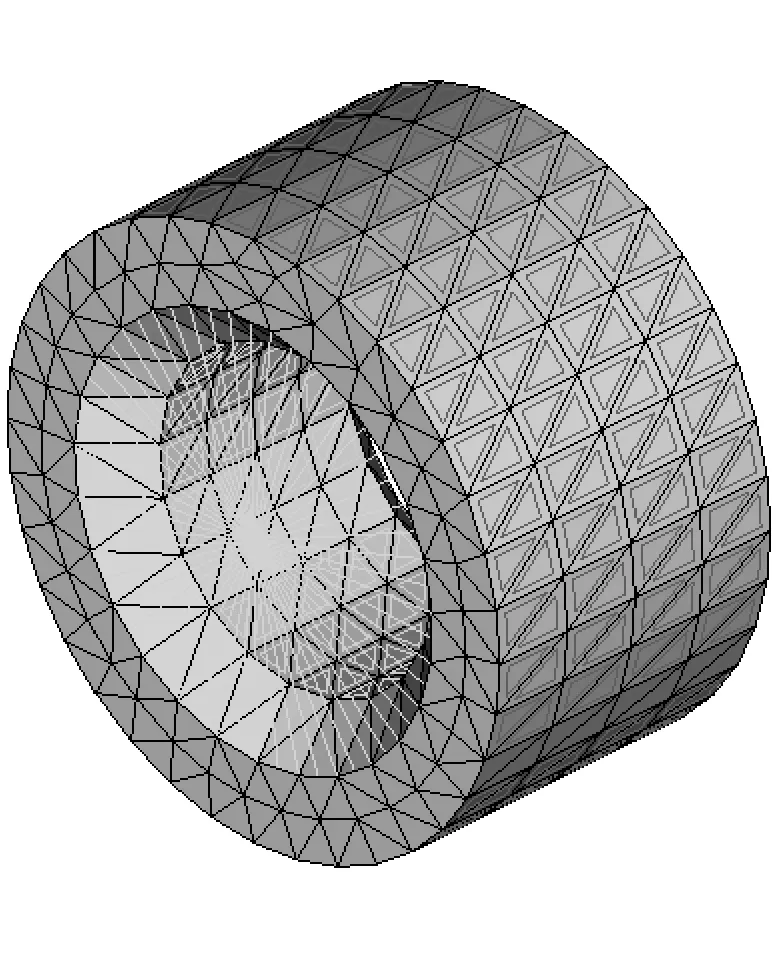
(c) 浮环轴承有限元模型

图2 增压器结构有限元模型

Fig.2 FEM models of turbocharger

2.2 EHD轴承模型建模

相比于刚性液力润滑轴承模型，EHD轴承充分考虑了接触表面的弹性变形、粗糙度和润滑油的黏压效应的影响。因此，将轴瓦、转子轴颈以及浮环轴承内外表面的节点定义为主自由度节点并进行模态缩减，将缩减好的节点建立相应的连接关系进行连接，浮环轴承多体动力学计算模型如图3所示。图中圆环为左右浮环，转子轴颈用直线表示，以便于观察轴承建模方式；浮环内轴承采用点对面的连接方式，将轴承内表面与轴颈连接，图中深蓝色即为内环油膜模型；将增压器壳体轴瓦与浮环轴承外表面采用面对面的连接方式，图中绿色即为外环油膜模型。

同时，为了更接近浮环轴承的实际工作状态以及提供更真实的润滑油油压边界条件，参考图4所示浮环轴承的实际几何模型，在浮环轴承中轴线剖面处沿周向均匀打6个油孔，油孔直径为1 mm。如此一来充分考虑了内外油膜间油压的相互影响，并将整个轴承模型的全局运动而产生的摩擦力以及油膜离心力计入多体动力学计算。

图3 EHD轴承计算模型

图4 浮环轴承几何模型

2.3 涡轮增压器基本参数

子结构模型和EHD模型建模完成后，按照涡轮增压器实际工作关系开展装配工作。其中浮环轴承参数设置是本次计算的重点，按照EHD轴承计算要求，浮环轴承计算所需参数包括轴承的基本结构参数、润滑油基本参数等，具体数值如表1所示。

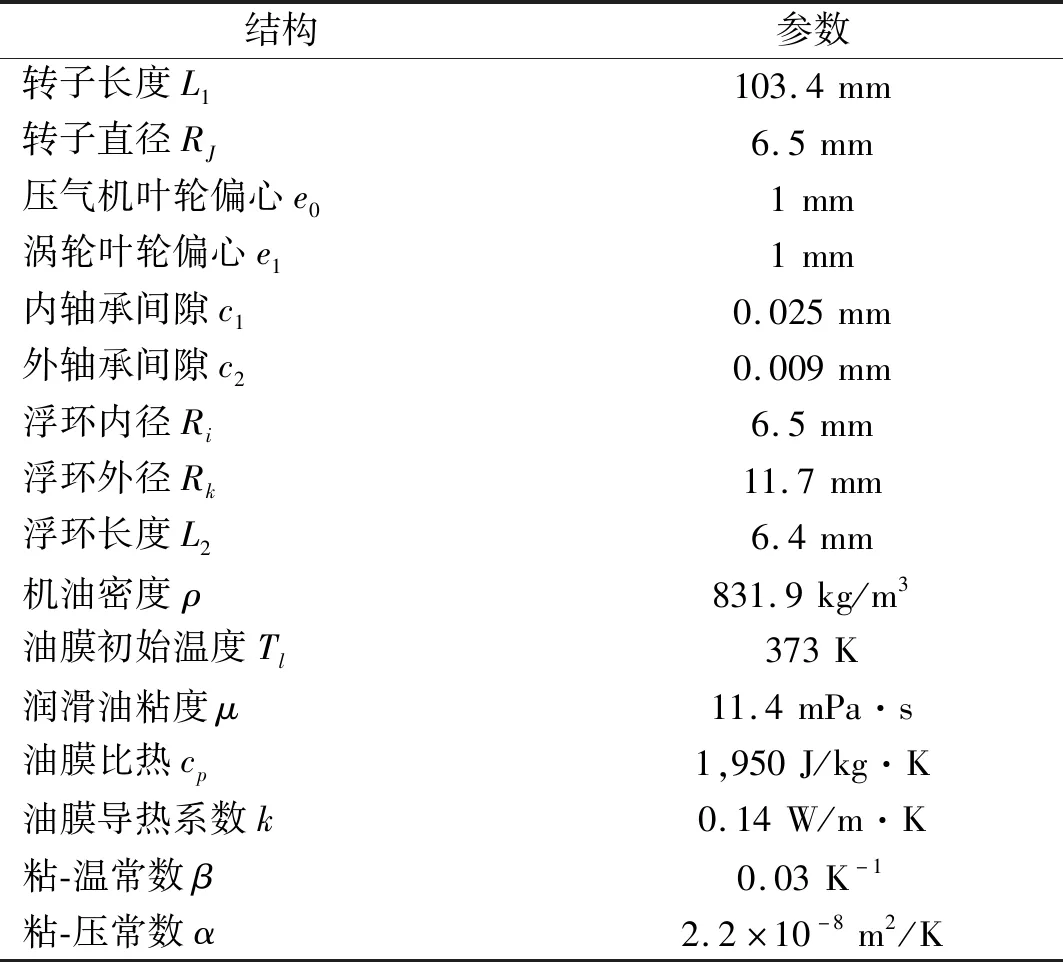
表1 涡轮增压器结构参数表

子结构装配与浮环轴承设置完成后，得到涡轮增压器的多体动力学计算模型，该模型用以模拟实际涡轮增压器的工作特性。

2.4 多体动力学边界参数

涡轮增压器在实际工作时，承受进排气的压力脉动、转子动平衡力、发动机激振力等复杂载荷形式，完全模拟增压器所受激励还存在较大的难度，本次计算重点考虑转子旋转引起的不平衡力对转子动力学以及增压器壳体振动特性的影响，计算时将转子转速施加到动力学模型中，完成计算模型边界设置。本示例中增压器工作转速在20 000～200 000 r/min之间，计算间隔为20 000 r/min。图5所示涡轮增压器多体动力学计算模型。

图5 涡轮增压器多体动力学计算模型

3 多体动力学结果分析

3.1 轴承油膜压力计算结果

在计算时，首先根据初始压力、初始油膜间隙等参数，采用公式(3)求解油膜厚度；然后根据公式(6)判断轴承摩擦状态，在液力润滑区采用公式(1)、(2)分别计算油膜压力，在混合摩擦区采用公式(5)求解油膜压力；然后将计算出油膜压力作为初始条件重复上述过程直至结果满足收敛精度。图6所示为不同转速下压气侧浮环轴承内油膜峰值压力计算结果对比，可以看出内油膜峰值压力受转速影响较大。在低速下浮环转速较低，油膜的楔形效应、挤压效应较为明显，体现在40 000 r/min时内油膜峰值压力较高；当转速提高到100 000 r/min时，浮环转速也明显提高，内油膜的工作环境有了较大改善，油膜峰值压力明显降低；随着转速进一步提高，在内油膜热负荷升高、转子倾斜量增大等因素的共同作用下，油膜峰值压力又开始升高。

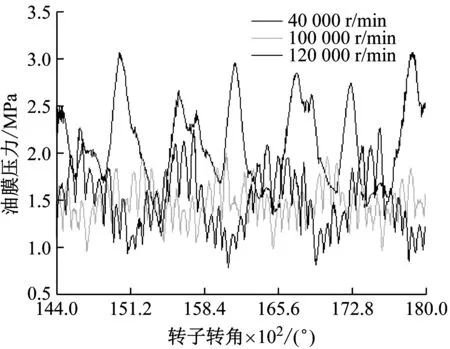
图6 不同转速下内油膜最大压力计算结果

图7为不同转速下压气侧浮环轴承外油膜峰值压力计算结果对比。外层油膜峰值压力只与浮环转速相关，从计算结果看，不同转子转速外油膜峰值压力的变化较小。

图7 不同转速下外油膜峰值压力计算结果

Fig.7 The simulation results of outer oil pressure at different rotor speed

3.2 转子振动特性分析

3.2.1 转子振动特性理论分析

由于转子存在偏心，增压器在工作时会产生明显的振动现象；转子偏心引起的振动与转子一阶振动频率保持一致，又称为同步振动，同步振动频率的表达式为

ω*=ωj

(9)

式中：ω*为涡轮增压器同步振动频率，ωj为转子一阶频率。

同时，浮环轴承的高速旋转会导致油膜在一定转速下产生涡动的现象。油膜涡动会引起转子失稳，从而导致增压器的振动噪声问题。由于浮环的存在，油膜涡动可分为内层油膜涡动与外层油膜涡动两部分，内外层油膜涡动频率可分别用公式(10)、公式(11)表示。从公式可以看出，油膜涡动引起的振动频率与转子一阶频率保持0.5倍关系，因此又称次同步振动。

ωin=0.5(ωj+ωr)

(10)

ωout=0.5ωr

(11)

式中：ωin为内层油膜涡动频率，ωout为外层油膜涡动频率，ωj为转子一阶频率，ωr为浮环一阶频率。

3.2.2 计算结果分析

图8所示为压气侧转子振动速度幅值、转速和频率的ColorMap图。从图中可以看出，转子在80 000 r/min以下的低速段存在显著的阶次振动现象，对应频率范围在1 250 Hz以下。从式(10)可知，此时的转子振动是由浮环轴承内油膜涡动引起的次同步振动；其中，在60 000 r/min以下由于浮环转速较低，此时振动频率与转子一阶频率呈现0.5倍关系；60 000～80 000 r/min之间，随着浮环转速逐渐增高，转子次同步振动频率与转子一阶频率的比值在0.5～1之间逐渐升高。根据公式(10)、公式(11)可以推断在该转速段，随着转速的增高，影响转子振动的因素逐渐依次为内油膜涡动、外油膜涡动、转子偏心，最终转子偏心引起的同步振动成为转子振动的主要形式。在转速80 000～120 000 r/min、频率1 250～2 000 Hz之间，由转子偏心引起的一阶同步振动是转子振动的主要成分；在转速120 000～160 000 r/min之间，内油膜涡动、外油膜的涡动以及转子偏心引起的振动现象均较为明显，对应频率范围为300～2 700 Hz；随着转速的进一步增高，在160 000～200 000 r/min之间，油膜涡动现象逐渐消失，增压器转子振动形式主要表现为转子偏心引起的一阶同步振动。

图8 压气侧转子振动ColorMap图

图9所示为涡轮侧转子振动ColorMap图，图中可以看出涡轮侧转子的振动特性与压气侧转子相似，在80 000 r/min以下的低速段存在较为显著的次同步振动现象，对应频率范围在1 250 Hz以下；在80 000～120 000 r/min区间内由转子偏心导致的一阶同步振动是转子振动的主因，对应频率为1 250～2 000 Hz；在120 000～160 000 r/min之间，转子内油膜涡动、外油膜涡动以及偏心量都会对转子振动产生较为显著的影响；在160 000～200 000 r/min之间，转子振动主要受偏心引起的一阶振动的影响。

图9 涡轮侧转子振动ColorMap图

Fig.9 The colormap result of rotor vibration performance at turbo side

3.3 增压器壳体振动计算结果

增压器多体动力学计算既可以得到转子振动特性，也可以得到增压器壳体振动特性，为进一步研究增压器的振动特性，提取增压器压气侧表面某测点处的振动计算结果进行分析。其中，增压器测点位置的选取应便于试验传感器的布置，以便对比验证。

图10所示增压器压气侧某点法向振动速度ColorMap图，从计算结果看，由转子偏心引起的一阶同步振动在增压器壳体振动中所占比例较大，而油膜涡动引起的增压器壳体次同步振动幅值相对较小；说明同步振动是该增压器壳体主要振动形式。

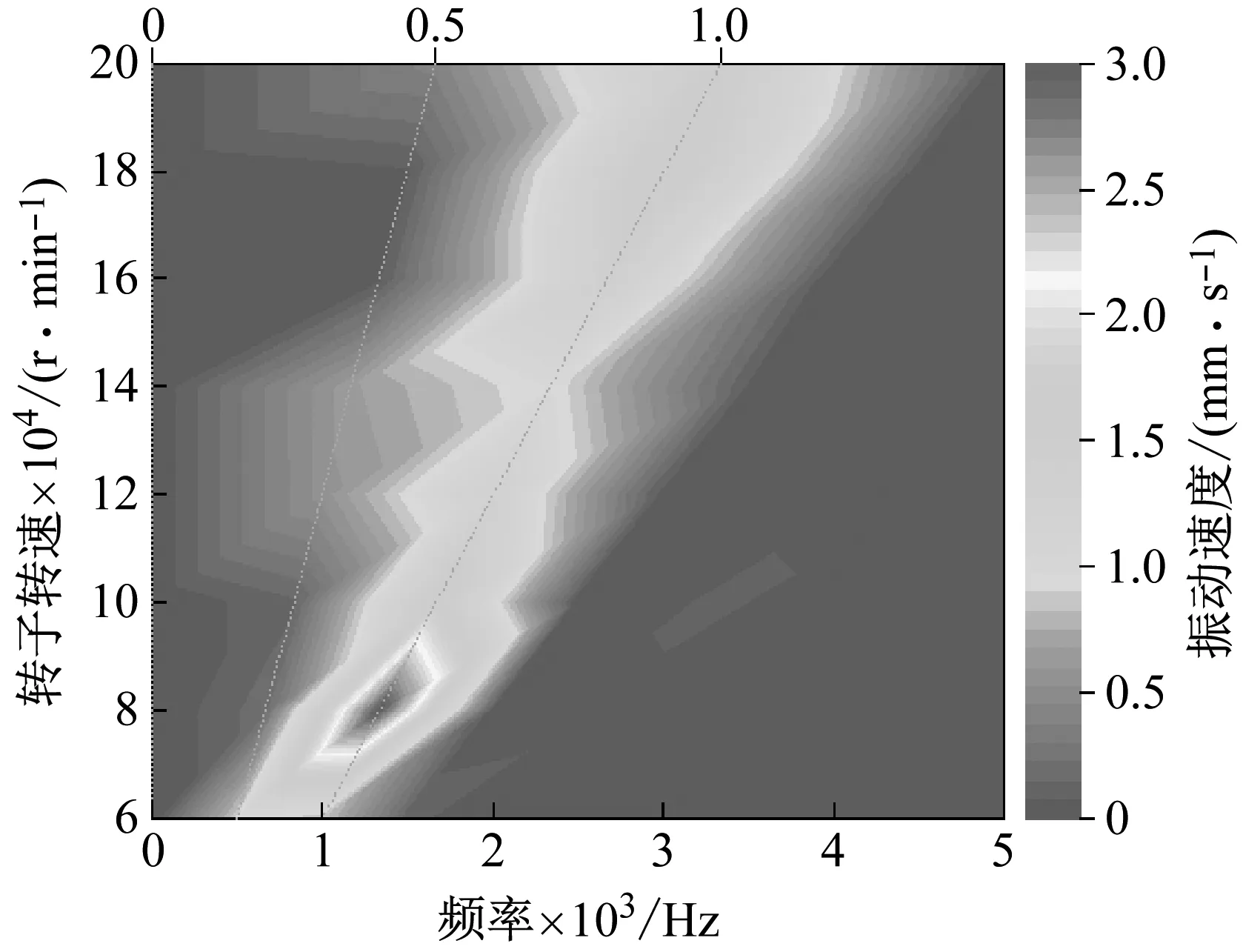
图10 增压器表面某点法向振动速度ColorMap图

Fig.10 The colormap result of turbocharger housing vibration performance (normal direction) at certain measurement point

从振动幅值特性看，增压器在60 000～100 000 r/min之间存在较为明显的振动峰值，中心转速为80 000 r/min，说明增压器在转子振动激励的作用下，出现了明显的共振现象；在100 000～140 000 r/min转速区间内，增压器振动有明显的缓解，该转速区间为增压器运转稳定且振动良好的“间歇区间”；在140 000 r/min以上的转速内，受到转子同步振动激励的影响，增压器壳体的同步振动随转速增高逐渐增大，同时还可发现增压器壳体该位置处振动特性受涡轮侧转子振动特性影响较大。

3.4 增压器振动特性实验分析

在半消声室中对该涡轮增压发动机进行台架试验，测取增压器压气侧表面某点的振动特性，试验测点布置如图11所示。试验工况为发动机转速1 100～6 000 r/min全负荷加速工况，测量该测点处三方向振动加速度信号，重点关注涡轮增压器垂向和横向振动特性。提取涡轮增压器垂向同步振动测试结果，并制作ColorMap图，如图12所示。

全负荷加速工况下，涡轮增压器在发动机1 500 r/min时介入工作，此时增压器转速为84 000 r/min，对应同步振动频率为1 400 Hz；随着发动机转速的不断升高，增压器工作转速逐渐增加到200 000 r/min，此时同步振动频率升高到3 300 Hz附近。根据测试结果，增压器在1 400～1 700 Hz附近，开始产生明显的同步振动现象，对应增压器转速84 000～102 000 r/min；在1 700～2 300 Hz附近，增压器同步振动现象减弱，此时对应转子转速102 000～138 000 r/min；同时，在2 300～3 300 Hz区间内，即转子转速138 000～200 000 r/min，增压器同步振动现象又逐渐增强。对比图9中涡轮增压器壳体的计算结果，可以发现实验值与计算值一致性较好，进一步证明了该位置处增压器壳体的振动受涡轮侧转子同步振动影响。

图11 增压器表面测点布置图

将图10增压器表面振动速度计算结果与图12表面振动实验结果进行对比可知，在100 000 r/min的低速区、100 000 ～150 000 r/min的中速区以及150 000 r/min以上的高速区，增压器表面振动计算结果曲线与实验曲线均在趋势上保持了较高的一致性，说明计算模型能够定性的预测实际增压器的同步振动特性。

图12 增压器表面某点法向振动速度测试结果

Fig.12 Test results of turbocharger housing vibration performance (normal direction) at certain measurement point

同时，通过实验结果与计算结果的对比可以看出，多体动力学仿真结果与实验值还存在一定的误差。主要有以下几点原因：①实验结果是台架上测量的涡轮增压器的实际工作状态，是发动机及台架上各种复杂情况的综合表现，与相对较为简单的计算模型必然存在差异；②计算模型在算法上还存在改进之处，如浮环轴承润滑模型还可以考虑油膜的热效应、增压器壳体及转子模型的建模方式等方面。

4 结 论

引入柔性体多体动力学与EHD弹性液力润滑理论对涡轮增压器进行多体动力学建模，对其振动特性进行了分析，并与实验结果进行了对比，本文的研究取得以下结论：

(1) 在转子全转速段内，涡轮增压器表面振动速度的多体动力学仿真结果与实验结果相比，其同步振动特性在趋势上均保持了较高的一致性，计算模型能够很好地预测涡轮增压器的同步振动特性。

(2) 浮环轴承内油膜峰值压力受转子转速影响较大，而外油膜峰值压力随转子转速变化不明显；增压器转子80 000 r/min以下时，其振动形式主要为油膜涡动引起的次同步振动，在80 000 r/min以上时主要振动形式为转子偏心引起的同步振动；增压器壳体在全转速段内的振动主要形式为同步振动，油膜涡动引起的次同步振动所占比例较小。

(3) 鉴于实验设计以及计算模型精度等方面的不足，目前还不能完全实现计算结果的定量对比，后续研究将会转向优化实验设计以及提高计算模型预测精度等方面。