高速铁路常用跨度简支箱梁竖向共振条件分析

2019-12-23孟鑫

振动与冲击 2019年23期

孟鑫

(1.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081；2.高速铁路轨道技术国家重点实验室，北京 100081)

截至2017年底，中国高速铁路总营运里程超过2.5万公里，位居世界第一。高速铁路多采用“以桥代路”的形式，桥梁约占线路总长度的57.7%，总孔跨数已超40万孔。正线主要采用标准跨径的预应力混凝土简支梁桥，跨度主要有24 m、32 m和40 m，其中以跨度32 m双线预应力混凝土简支箱梁为主型梁。我国高速铁路桥梁存在设计等级、轨道结构、截面形式等的不同，铁路总公司颁布了多套简支箱梁通用图纸。

铁路桥梁发生竖向共振是由于桥梁自振频率与列车对桥梁的加载频率之间的特有关系引起的。列车速度达到某一特定的值时，列车各轴之间的加载频率就会接近桥梁结构自振频率，从而引起共振。固定编组的动车组列车对桥梁的竖向加载频率主要取决于列车速度和车长，而轴距、定距、两车相邻转向架的中心距由于重复作用不连续，相对处于次要地位[1]。文献[2]认为：同类型的车辆通过中小跨度简支箱梁桥时移动的轴荷载将使桥梁发生共振，高速范围内的共振将使桥梁冲击系数变得相当大。文献[3]认为：高速铁路简支箱梁存在共振和消振现象，简支箱梁共振中的车长占主导地位。文献[4]分析认为，列车以一定速度通过桥梁时，根据发生机理的不同，简支箱梁可能发生几种不同形式的共振。

本文在桥梁共振条件理论分析的基础上，结合高速铁路常用跨度预应力混凝土简支箱梁自振特性和竖向动力响应实测数据，分析研究动车组列车以不同速度通过简支箱梁时可能发生的共振速度和超谐共振速度及相应的桥梁竖向共振机理，可为铁路工务养护维修、优化梁体设计和完善评价标准提供指导和依据，具有重要的理论和工程意义。

1 简支箱梁共振理论分析

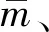
列车模型如图1中所示，固定轴距为lw，定距为lc，车辆全长(钩到钩距离)为lv。为推导方便，将列车轴重排列简化为N个间距为d的移动集中荷载列。

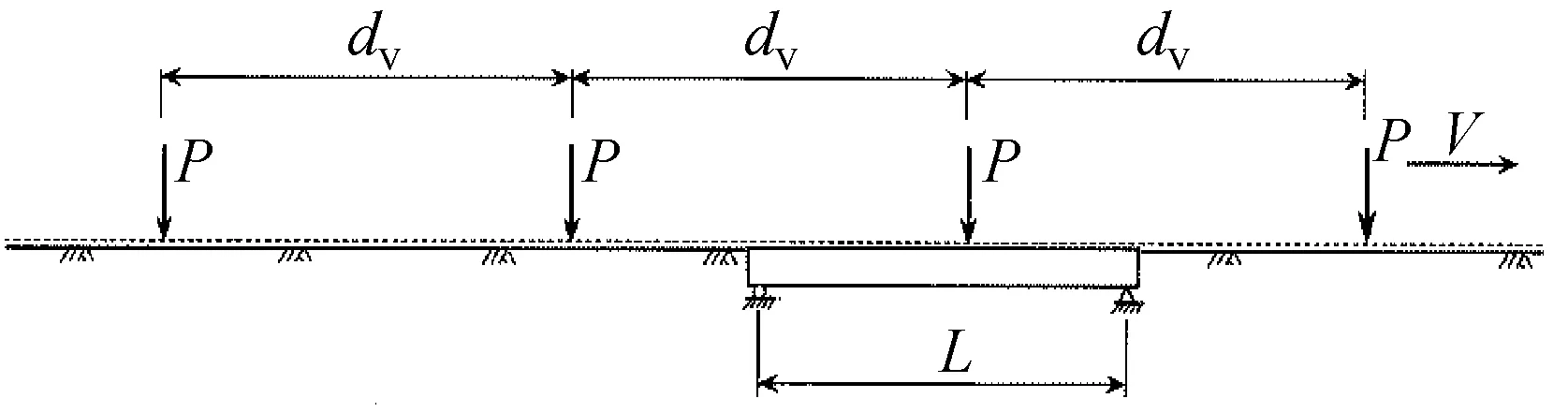
图1 列车作用与桥梁示意图

车辆通过桥梁时的运动平衡方程为：

[H(t-tN)-H(t-tN-L/v)]

(1)

式中:u(x,t)为竖向动位移，δ为Dirac函数，H(ξi)为分段函数，N为总的车辆数；tk=(k-1)dv/v。

求解方程(1)得：

Q2(v,t)H(t-tN-L/v)]

(2)

其中：

(3a)

(3b)

1.1 桥梁共振

当sin(ω0d/2v)=0或ω0d/2v=iπ,(i=1,2,3,…)时，式(3b)的主要部分可能消失，此时桥梁响应达到最大。对于给定车长d和跨度Lb，共振条件为：

(4)

式中：vres,i为引起桥梁共振的列车速度(km/h)；fbv为桥梁的竖向自振频率(Hz)；d为车长(m)。

由式(4)可知，当加载频率v/3.6d等于桥梁的自振频率 1/i(i=1,2,3,…)时会使结构发生共振或超谐共振，当i=1时，定义vres,1为桥梁的共振速度，当i=2，3时，定义vres,2、rres,3为2、3阶超谐共振速度。

当i=1,2,3,…时，相应的S=0.5d/L，0.25d/L，0.167d/L,…，随着i的增大，S值逐渐减小。当列车从低速到高速以不同的速度通过桥梁时，桥梁竖向动力响应出现峰值。但是，i>3时的速度参数S均很小，式(3a)与(3b)中的1/(1-S2)随着S的减小而减小。

1.2 桥梁消振

当满足条件cos(π/2S)=0时，式(3b)为0，即不存在已通过桥梁的前N-1个集中力引起的桥梁自由振动的余振响应，此时称为简支箱梁的消振状态。当满足消振条件时，简支箱梁的竖向动力响应取决于最后一个集中荷载，消振条件与阻尼无关。

满足消振条件时速度参数为：

(5)

即：

(6)

式中：vc,i为引起桥梁消振的列车速度(km/h)；fbv为桥梁的竖向自振频率(Hz)；L为桥梁跨度(m)。从式(6)中可以看出，消振速度与桥梁本身的特性相关，与列车类型、列车车长无关。

①当共振速度参数S=0.5d/L时，移动荷载列引起梁体的共振，实际上通过选择“跨度/车长(L/d)”，让共振速度参数S=0.5d/L满足消振条件(5)就可以抑制共振，即不存在共振的L/d为：

(7)

对于我国高速铁路而言，运营动车组车长一般为25 m，则L/d=1.5(L=37.5 m)时，梁体不会出现共振现象。

②当第2超谐共振速度参数S=0.25L/d时，通过选择“跨度/车长(L/d)”，满足消振条件式(5)就可以避免2阶超谐共振，即不存在2阶超谐共振的L/d为：

(8)

当L/d=0.75(L=18.75 m)或1.25(L=31.25 m)时，梁体不会出现2阶超谐共振现象。

采用自编车桥耦合分析程序，根据我国高速铁路桥梁常用跨度简支箱梁竖向自振频率实测结果，计算不同速度下桥梁跨中竖向振幅最大值，绘制了速度v、L/d和竖向振幅的三维图，如图2所示。从图中可以看出，当L/d=1.5、0.5时，在移动荷载作用下，桥梁共振响应被抑制，桥梁竖向动力响应很小。

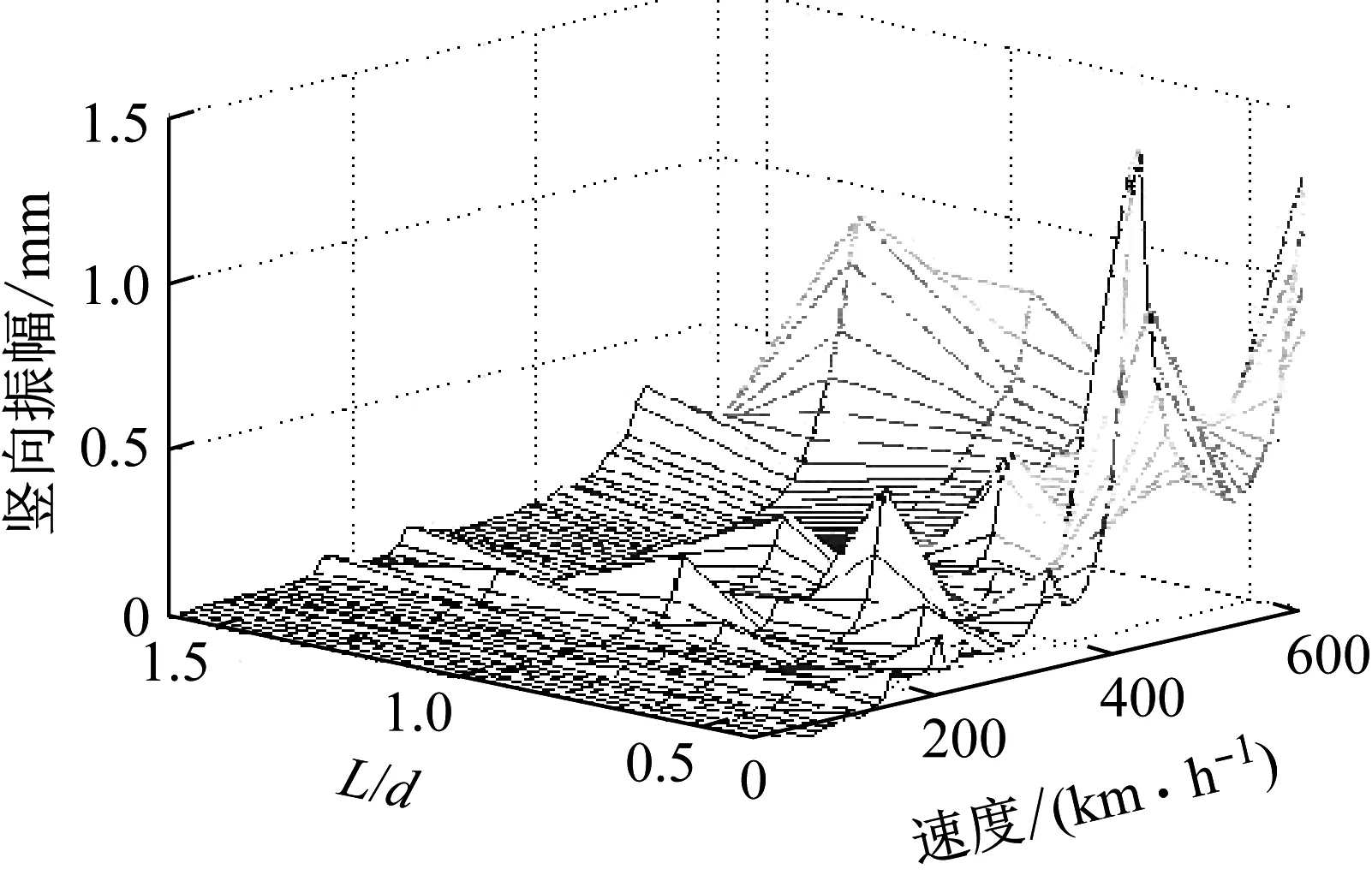
图2 不同跨度/车长(L/d)时简支箱梁竖向振幅与速度关系图

Fig.2 The graph of vertical amplitude and train speed in differentL/d

2 简支箱梁竖向动力特性

2.1 竖向自振频率限值分析

自振频率是桥梁动力特性关键参数，也是反映结构刚度的重要指标。研究表明：列车通过自振频率过低的桥梁时，会产生较大的动力响应；梁体自振频率与车桥共振速度直接相关；桥梁结构发生共振时，车体和梁体均产生较大的振动响应[5]。

欧盟规范“Eurocode 1: Actions on structures-Part 2: Traffic loads on bridges”中明确了高速铁路桥梁设计中动力分析流程和检算内容，提出了不需进行动力分析的激振波长限值[6]：

(9)

式中:vmax为设计最高车速(m/s)；f0为桥梁的竖向自振频率(Hz)。

日本分别于2004年颁布了《铁路结构物设计标准及解释—混凝土结构物》、2006年颁布了《铁路结构物设计标准及解释—变位限制》，提出了桥梁动力系数查照图表。指出当速度参量α>0.33时，将引起较大冲击，即：

(10)

式中:v为列车速度(km/h)。

《高速铁路设计规范》(TB 10621—2014)根据我国高速铁路桥梁设计中大量车桥耦合分析结果制订了简支梁的基频下限值，并在综合分析桥梁动力响应与列车类型、运行速度、桥梁刚度关系的基础上，提出了我国CRH系列动车组列车在不同设计速度条件下、跨度40 m以下的双线简支箱梁不需进行车桥耦合动力分析的自振频率(基频)限值。

对于设计速度250 km/h和350 km/h的常用跨度简支箱梁，欧盟规范和我国规范中不需进行动力分析的竖向自振频率限值及日本规范中避开较大冲击的频率比较见表1。从表中可以看出，我国《高速铁路设计规范》规定不需动力检算的梁体竖向自振频率限值与日本规范接近，略低于欧盟规范。

表1 常用跨度双线简支箱梁不需动力检算竖向自振频率限值

Tab.1 The limit for natural frequency of the simple supported box girder which doesn’t need dynamic calculationsHz

跨度/m设计速度250km/h350km/h中国欧盟日本中国欧盟日本128.33/8.7710.00/12.28166.2510.686.587.5012.469.21205.006.515.406.157.607.55244.174.974.485.966.766.27323.813.683.344.765.074.68

以高速铁路桥梁中数量最多的32 m简支箱梁为例，实测32 m简支箱梁竖向自振频率见表2。竖向自振频率实测值满足规范限值、设计值的要求。不同梁型的32 m简支箱梁竖向自振频率实测值与设计值相比明显提高，最大值提高了34%。存在差异的原因主要是混凝土实际弹模较大、二期恒载变化、轨道板与梁相互作用及支座摩阻等[7-10]。自振频率实测值远大于规范中不需进行动力检算的限值，通过提高32 m简支箱梁的竖向自振频率，同时提高了车桥耦合共振速度，在目前的运营速度(350 km/h)范围内桥梁不会发生共振现象，但可能存在高阶超谐共振现象。

表2 实测32 m简支箱梁竖向自振频率

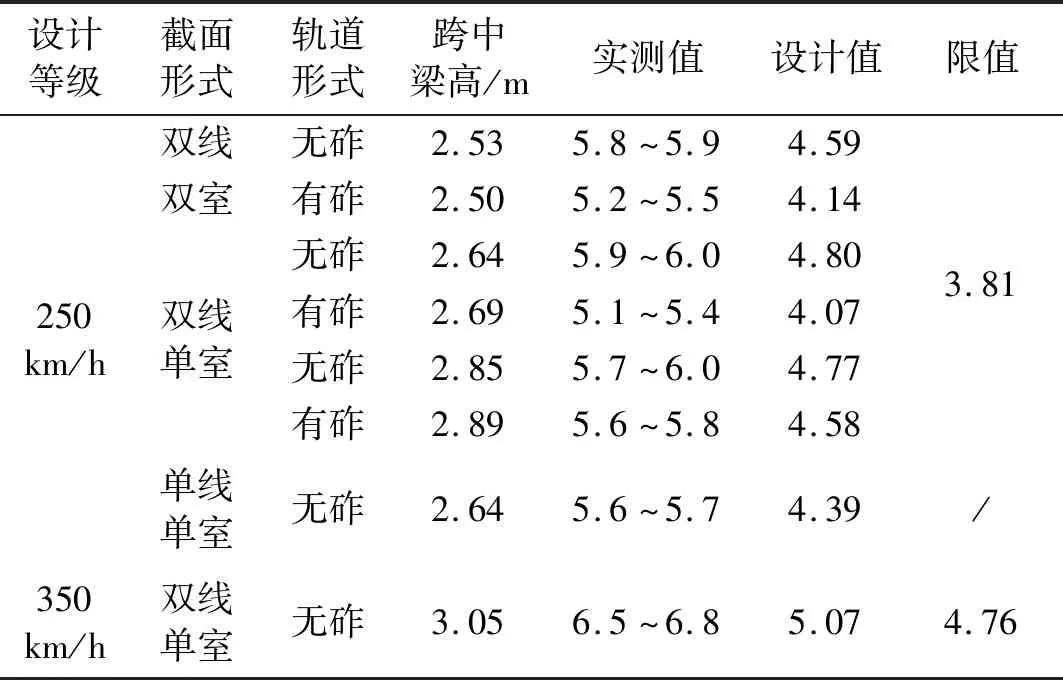
Tab.2 The measured value of 32 m box girder Hz

2.2 竖向动力响应数据分析

2.2.1 32 m简支箱梁

根据简支梁共振、消振理论，结合我国高速铁路32 m简支箱梁竖向自振频率实测结果，动车组车长d取25 m，L为桥梁跨度31.5 m。32 m简支箱梁共振、超谐共振、消振计算速度见表3。计算结果表明：在运营速度(350 km/h)范围内，32 m简支箱梁不会出现1阶共振现象；由于2阶超谐共振速度和3阶消振速度重合，2阶超谐共振被抑制；3阶之后的超谐共振速度与对应的消振速度均有一定差距，理论上存在超谐共振现象。

表3 32 m简支箱梁共振、超谐共振、消振计算速度

Tab.3 The resonance speed, super-harmonic resonance speed and cancellation speed of 32 m box girderkm/h

设计等级及频率峰值状态振动阶数12345250km/h5.1～6.0Hz超谐共振459～540230～270153～180115～13592～108消振1157～1361385～454231～272165～194128～151350km/h6.5～6.8Hz超谐共振585～612293～306195～204146～153117～122消振1474～1542491～514295～308211～220164～171

以设计等级250 km/h、自振频率为5.9 Hz，设计等级350 km/h、自振频率为6.8 Hz的两孔32 m简支箱梁实测数据为例。实测动车组列车以不同速度(125～327 km/h)通过桥梁时，跨中梁体竖向加速度(20 Hz低通滤波)散点分布见图3和图4。

由梁体竖向加速度与列车速度关系图可知，两孔32 m简支箱梁(5.9 Hz、6.8 Hz)的2阶超谐共振速度与3阶消振速度接近，分别为266 km/h、268 km/h和306 km/h、308 km/h，实测梁体动力响应未出现峰值，说明桥梁2阶超谐共振被抑制。实测两孔32 m简支箱梁(5.9 Hz、6.8 Hz)动力响应在列车177 km/h、204 km/h通过时存在明显峰值，与3阶超谐共振速度计算值吻合，32 m简支箱梁存在明显的3阶超谐共振现象，超谐共振时的动力响应数值大小与试验最高速度时接近。实测32 m简支箱梁4阶消振现象明显，实际的消振速度范围与计算值191 km/h、220 km/h相比更宽。当列车以4阶及以上的超谐共振速度(150 km/h以下)通过桥梁时，32 m简支箱梁动力响应未出现振动峰值，实测动力响应数值均较小，可认为32 m简支箱梁4阶及以上的超谐共振现象不明显。

图3 32 m简支箱梁(5.9 Hz)梁体竖向加速度与速度关系图

Fig.3 The graph of vertical acceleration and train speed in 32 m box girder (5.9 Hz)

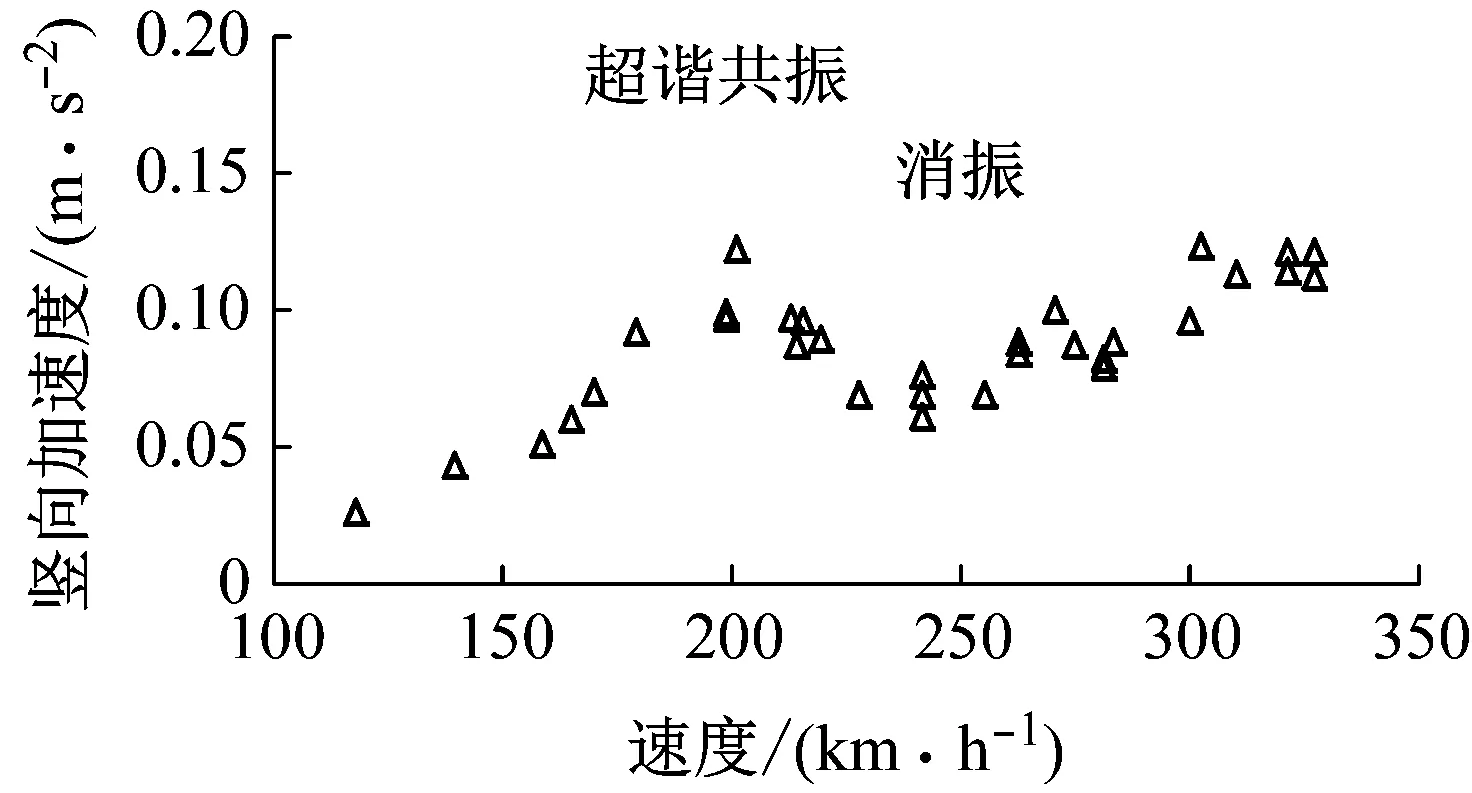
图4 32 m简支箱梁(6.8 Hz)梁体竖向加速度与速度关系图

Fig.4 The graph of vertical acceleration and train speed in 32 m box girder (6.8 Hz)

在动车组列车以3阶超谐共振、4阶消振速度作用下，32 m简支箱梁实测跨中梁体竖向挠度时域波形见图5。动车组以超谐共振速度通过时，随着各节动车组列车的连续规律加载，梁体挠度值增大趋势明显，列车轮对作用与梁体的轨迹清晰；当动车组出桥后，梁体挠度余振持续时间较长。动车组以消振速度通过时，挠度波形无明显增大现象，出桥后梁体挠度也无明显余振。实测梁体应变波形与挠度波形趋势一致。

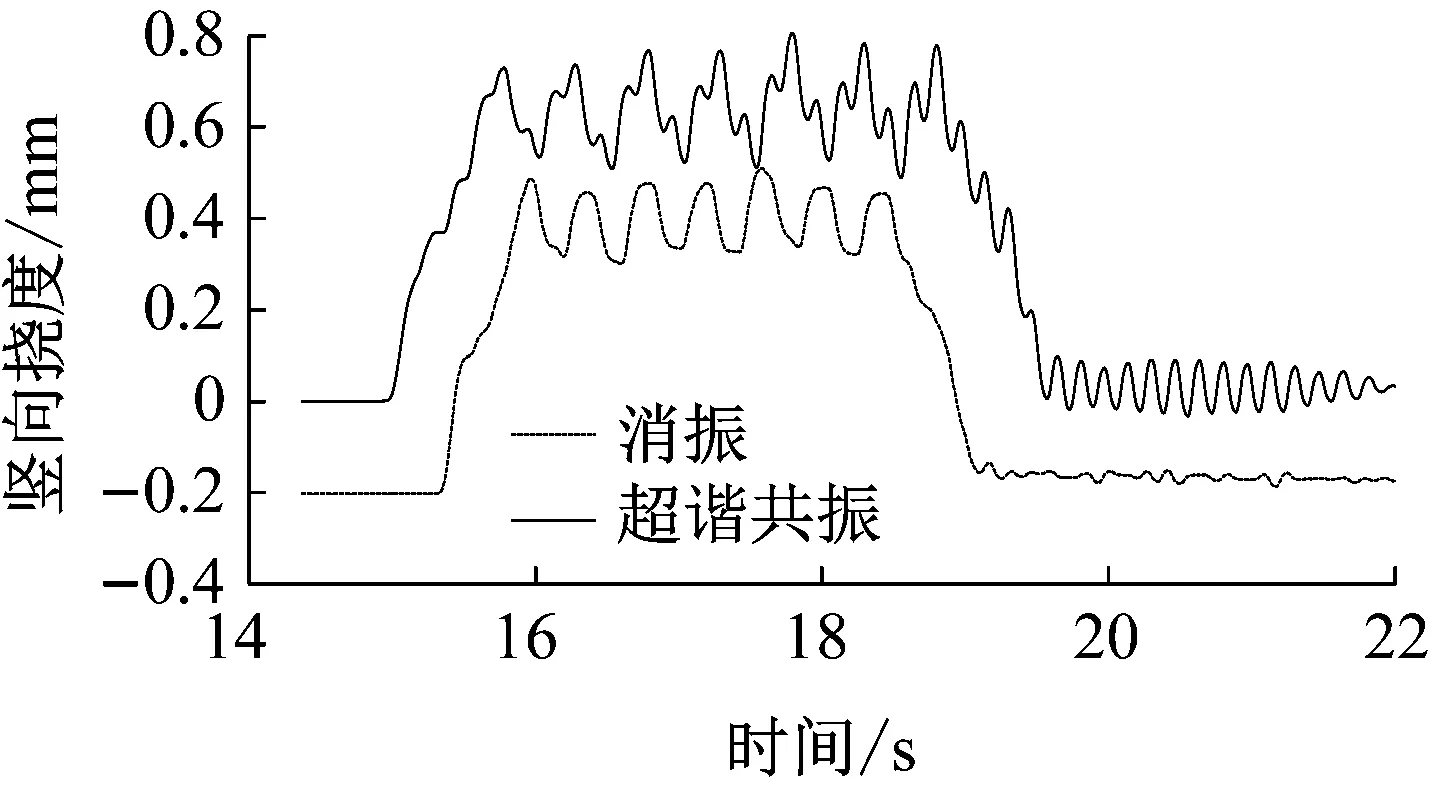
图5 实测32 m简支箱梁跨中竖向挠度时域波形

动力系数反映了列车对桥梁冲击作用，我国高速铁路规范中采用运营动力系数进行评价。实测32 m简支箱梁跨中挠度动力系数与列车速度关系见图6，当动车组实际的运营速度与32 m简支箱梁3阶超谐共振速度接近时，动力系数出现峰值，与应变动力系数趋势一致。某线32 m简支箱梁在动车组200 km/h作用下的动力系数存在超出运营动力系数的现象，说明列车冲击作用明显，应引起桥梁养护部门足够的重视。

图6 32 m简支箱梁跨中挠度动力系数分布

2.2.2 40 m简支箱梁

某设计等级350 km/h高速铁路40 m简支箱梁，实测竖向自振频率为5.86 Hz，动车组最高试验速度为385 km/h。40 m简支箱梁计算共振速度495 km/h，实际中未达到此速度，对应的2阶超谐共振速度为264 km/h，3阶消振速度338 km/h。实测跨中梁体竖向加速度与行车速度关系见图7，梁体竖向加速度在260～270 km/h时出现峰值，在330～340 km/h时为低谷值。动车组列车以2阶超谐共振速度和3阶消振速度通过时，跨中梁体竖向振幅时域波形比较见图8。从图中可以看出，消振时梁体的动力响应明显小于2阶超谐共振时的动力响应，消振时对应的竖向振幅最大值约为2阶超谐共振时的一半。

图7 40 m简支箱梁跨中竖向加速度与速度关系图

Fig.7 The graph of vertical acceleration and train speed in 40 m box girder

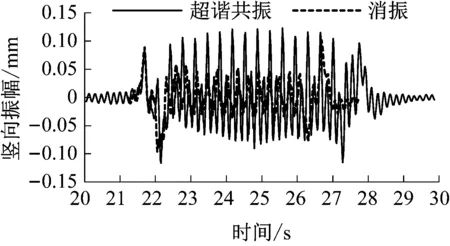
图8 40 m简支箱梁2阶超谐共振与消振时竖向振幅对比图

Fig.8 Waveform of vertical amplitude about the second super-harmonic resonance speed and cancellation speed in 40 m box girder

2.2.3 24 m简支箱梁

某设计等级250 km/h高速铁路24 m简支箱梁，实测竖向自振频率为9.4 Hz，动车组最高试验速度为275 km/h。24 m简支箱梁计算共振速度为846 km/h，实际中未达到此速度，3阶、4阶超谐共振速度为212 km/h和282 km/h，4阶消振速度为227 km/h。实测梁体竖向加速度随速度变化的关系见图9，3阶超谐共振速度时的桥梁动力响应远大于4阶超谐共振。24 m简支箱梁3阶超谐共振和4阶消振时梁体跨中竖向振幅时域波形对比见图10。从图中可以看出，4阶消振时梁体的动力响应略小于3阶超谐共振。

图9 24 m简支箱梁跨中竖向加速度与速度关系图

Fig.9 The graph of vertical acceleration and train speed in 24 m box girder

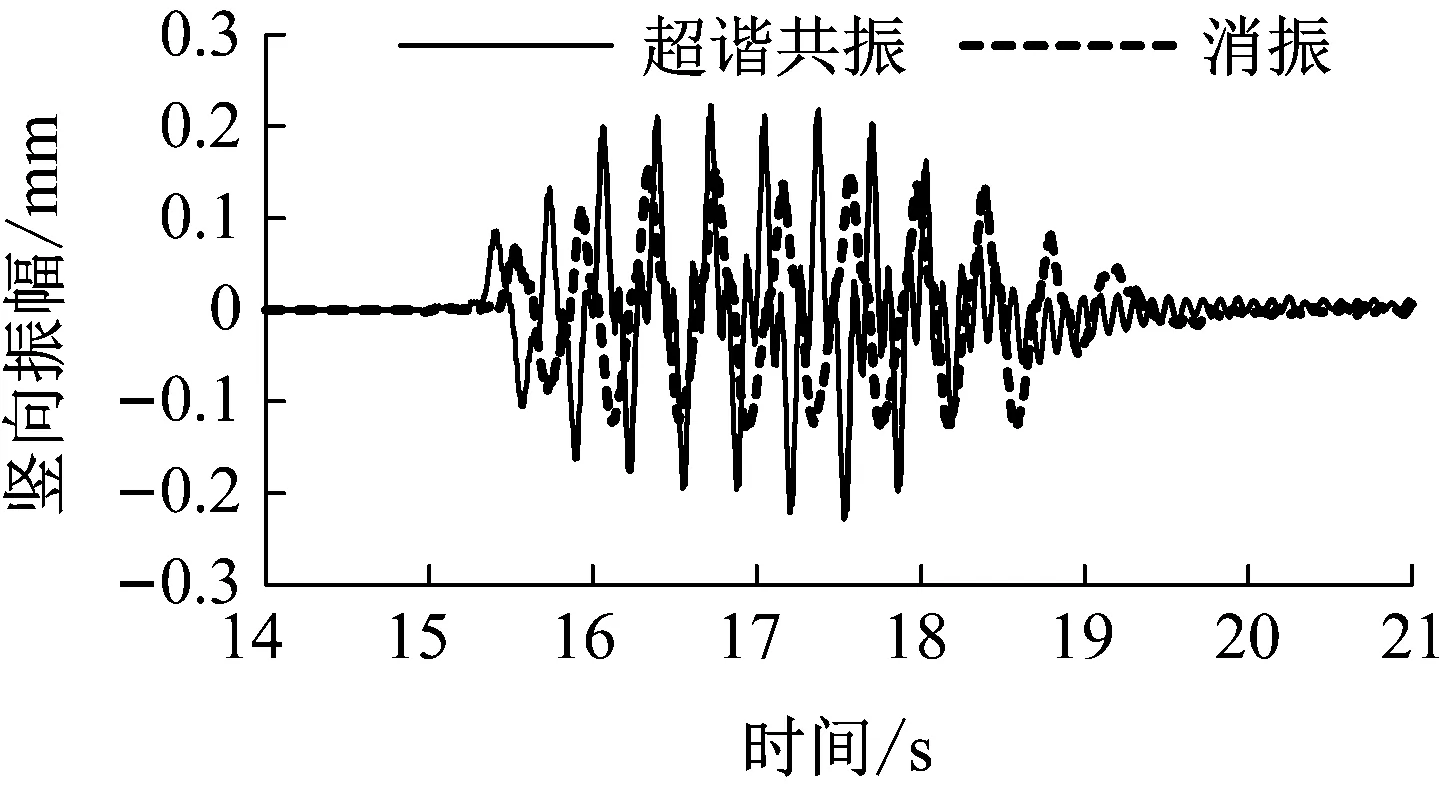
图10 24 m简支箱梁4阶超谐共振与消振时竖向振幅对比图

Fig.10 Waveform of vertical amplitude about the fourth super-harmonic resonance speed and cancellation speed in 24 m box girder

2.3 综合分析

通过对高速铁路40 m、32 m和24 m简支箱梁的共振条件理论分析和实测数据对比表明，我国高速铁路常用跨度简支箱梁在运营速度范围内不会出现共振现象，但存在2阶、3阶、4阶超谐共振现象，梁体动力响应出现峰值效应，与理论分析结果吻合较好。

当梁体发生超谐共振时，实测梁体应变、振动、挠度的时域波形会产生明显变化，应综合各类数据进行对比分析。当不同传感器、不同测试方法反应出的梁体动力响应规律一致时，才可判定桥梁产生了超谐共振。其中，梁体加速度、挠度波形对超谐共振现象最为敏感，需重点关注。为方便现场分析，可将高速铁路常用跨度简支箱梁的超谐共振速度公式vres,i=3.6f×d/i,(i=1,2,3,…)进行简化，得到简支箱梁超谐共振速度预估公式见表4。式中，v为超谐共振速度(km/h)，f为梁体竖向自振频率(Hz)。

表4 简支箱梁超谐共振速度(km/h)预估公式

Tab.4 The calculation formula of super-harmonic resonance speed about the simple supported box girder

超谐共振预估公式备注2阶v=45f常见于40m梁3阶v=30f常见于24m、32m梁4阶v=22.5f常见于24m梁

当高速铁路简支箱梁超谐共振发生时，实测梁体竖向动力响应数值仍较小，分析原因认为：①简支箱梁在列车通过时的有载频率在一个范围内变化，而不会固定在某一频率上，激励频率与简支箱梁的有载频率不可能完全一致；②目前设计的简支箱梁具有足够的刚度具有较大的安全裕量；③由于简支箱梁自重较大(大于700 t)、阻尼的作用及动车组质量较小(轴重一般小于16 t)、编组较短，激励能量有限。

在高速铁路运营期间，不同型式桥梁结构的超谐共振速度应引起重视，列车通过时的速度应尽量避开超谐共振速度。桥梁作为重要的线下基础，梁体较大的振动响应会直接影响桥上无砟轨道结构稳定性、道砟的状态，也会对列车通过桥梁时的稳定性造成影响。工务部门对桥梁进行养护维修时，列车以桥梁超谐共振速度通过的区段应列为检查重点，应加强对梁体及线路不平顺、扣件、道床板与支撑层连接处的观测和养护。