基于非线性均匀化的类岩石材料多尺度计算方法研究
2019-12-23王庆姚俊谭文禄潘惠惠
王庆,姚俊,谭文禄,潘惠惠
(中电建生态环境集团有限公司,广东深圳518102)
岩石等复合材料是在小到一定的尺度上都具有非均质性[1],这些微细观尺度上的非均质性对材料的宏观物理力学性质具有很大的影响。由于微细观结构的复杂性和多样性,采用实验的方法测量不同微细观结构的宏观等效性质需要花费大量的时间和代价,因此许多学者倾向于寻求多尺度计算方法[2,3]来建立复合材料的微细观结构和宏观等效性质之间的关系。
多尺度计算方法有许多不同的分类方法[4-6],根据宏细观模型间信息的传递方式不同,主要分为3类:递阶法[7](Hierarchical multiscale method),准协同法[8](Semi-concurrent multiscale method)和协同法[9](Concurrent multiscale method)。递阶法在细观模型数值试验之前,首先假定一种典型的宏观本构模型,如弹性、塑性、黏塑性等,这些宏观本构模型中的未知参数,可以根据在细观模型上进行的数值试验结果数据拟合得到,递阶法只能处理线性问题和宏观本构关系简单的非线性问题。准协同方法的宏观模型和细观模型是分开计算的,在计算过程中,宏细观模型之间信息是双向传递的,不需要事先知道宏观的本构关系,因此可以处理复杂的非线性问题。协同方法的特点是能将细观模型的网格直接嵌套在宏观模型的网格中,细观模型的求解直接在宏观模型中进行,所以不需要进行尺度分离,但需要大量的存储空间和计算代价。因此选择递阶法既可以处理损伤、裂纹扩展等复杂非线性问题,也可以避免大量的存储空间和计算代价。
最常见递阶法是计算均匀化方法,包括线性和非线性,其中线性计算均匀化方法只能处理线性问题,但是岩石等材料在变形过程中存在细观结构的非均质性以及不同组分之间的相互作用,这种不同组分之间的相互作用在断裂多尺度计算中必须要考虑,因此本文选择用非线性计算均匀化方法来研究岩石等材料的裂纹扩展规律。
1 非线性多尺度控制方程
1.1 增量控制方程
非线性计算均匀化方法是基于渐进展开[10]的思想得到的,其与线性计算均匀化方法控制方程的推导过程[11]最大的区别是细观结构在变形过程中材料参数会发生变化,所以控制方程必须是增量形式。考虑一种非均质的材料的宏观空间区域是Ωε,边界为Γε。该材料具有某种周期性的细观结构,该细观结构具有表征体积单元RVE,其细观空间区域表示为Θ。Ωε中该材料的基本控制方程可以表示为:
(1)
(2)
(3)
位移和力边界条件为,
(4)
(5)
1.2 增量位移的渐进展开
按照渐进展开理论,宏细观模型坐标是相关的[12],假设宏观模型坐标为x,细观模型坐标为y,增量形式的位移、应力和应变可以用尺度因子ε形式表示为:
(6)
(7)
(8)
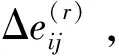
(9)
(10)
(11)
将增量应变式(7)代入到本构关系式(2)中可以得到增量应力:
(12)
将增量应力式(8)代入到平衡方程式(1)中,根据尺度因子ε进行组合,可以得到不同阶的平衡方程:
(13)
(14)
(15)
1.3 宏细观控制方程
求解不同阶的平衡方程式(13)—(15),得到宏细观控制方程和信息传递方程如下。
a) 宏观问题
(16)
b) 细观问题
(17)
c) 宏细观信息传递
(18)
(19)
式中N + 1〈σij〉y、N〈σij〉y——第N、N+1步的宏观应力。
2 非线性计算均匀化方法的实现
2.1 一般过程
非线性计算均匀化方法的一般过程可以分为4步,见图1。利用细观模型计算出来的等效切线模量和等效应力求解宏观方程(16),得到宏观应变;将第1步中得到的宏观应变作为边界条件施加到细观模型上,求解细观方程(17),得到细观模型的应力等状态量;根据第2步的计算结果按式(18)、(19)求解宏观模型的等效切线模量和等效应力;回到第1步进行下一个增量步的循环,直到加载完成。
2.2 周期性RVE的生成
本文的数值案例中使用的材料是水泥砂浆,具体成分是砂子、水泥和水,其水灰比为0.4,砂子重量占40%,水泥砂浆和砂子的密度分别为2 000、2 650 kg/m3,在不考虑气孔的情况下,细观结构中基质和砂子的体积比分别为67%和33%。砂子采用的粒径小于0.5 mm的河砂,假设砂子的粒径满足在区间[0.3, 0.5] mm之间的均匀分布。
从非线性多尺度控制的边界条件中可以看出,RVE的细观结构必须具有周期性。选择用第顺序投放方法[13]来生成水泥砂浆的细观模型,但是为了使产生的细观模型具有周期性,所以要在顺序投放方法基础上进行改进。周期性RVE中的球体主要分为4类,见图2。
a) 内部球体。远离RVE边界的球体是内部球体,可以用传统的顺序投放方法产生。
b) 面上的球体。当1个球体与RVE的面接触时,会在对应的面上复制1个相同的球体,原来的球体称为主体,复制的球体称为从体。
c) 棱上的球体。当1个球体与RVE的棱接触时,会在其它3条棱上复制3个从体。
d) 顶点上的球体。当1个球体与RVE的顶点接触时,会在其它7个顶点上复制7个从体。
以大小为(4×4×4) mm3的RVE举例说明周期性RVE的生成,水泥砂浆的细观结构见图3。
2.3 一般过程的实现
在非线性计算均匀化方法中,宏观模型的本构关系是不需要知道的,可以在加载过程中通过细观模型确定的。宏观应力和切线模量是随着RVE的变形而变化的,在不知道显式本构关系的情况下求解宏观问题,必须依靠ABAQUS中的用户子程序UMAT。UMAT有2个变量需要用户返回给ABAQUS主程序,一个是Jacobian矩阵∂Δσ/∂Δe,这与宏细观传递信息中的切线模量相对应;另一个是增量应力,这与宏细观传递信息中的增量应力相对应。UMAT的调用都是在单元的高斯积分点上进行的,在第k+1步的宏观模型中的每个单元的高斯积分点中,ABAQUS调用UMAT的流程见图4。
3 非充填预裂纹的单轴压缩试验
3.1 试样及加载系统
预裂纹压缩试验中用到的试件材料是水泥砂浆,其配比在前面有所介绍,其它试验条件和结果可见Zhuang的预裂纹试验[14]。试样均采用70 mm×70 mm×140 mm尺寸的标准长方体,预裂纹为贯通型,试样及预裂纹的几何形态见图5。裂纹厚度为1 mm,长度为15 mm,倾角α在有15、30、45、60、75°几种,主要研究不同倾角下的裂纹扩展规律。试验采用无侧限单轴加载,加载速率为0.25 kN/s,预加荷载为1 kN,加载5 kN为一步,每步完成后停止加载5 s,进行裂隙周边拍照记录。
3.2 非充填预裂纹的扩展特征
按裂纹扩展的几何形态和破坏机制的不同,将原始裂隙周边新生裂纹分为3类[15]:翼裂纹、反翼裂纹与次生裂纹,见图6。新生裂纹的扩展特征主要包括起裂点,起裂顺序和起裂角,其中翼裂纹的起裂角定义见图7。
4 数值算例
4.1 多尺度模型
非充填预裂纹的单轴压缩试验的多尺度模型见图8。由于非线性多尺度计算是在每个单元的高斯积分点上进行,需要的计算代价比较大,因此只考虑预裂纹附近的材料的非均匀性,用红色单元表示;远离预裂纹(距离超过3倍预裂纹厚度)的材料则是均匀材料,用绿色单元表示。多尺度材料的细观结构见图3。宏观模型的下边界约束y方向位移,左右边界自由,上边界施加位移加载方式。
4.2 本构关系和参数
细观模型中的基质和颗粒采用混凝土塑性损伤本构模型[16],其单轴拉伸和压缩应力应变曲线见图9。
出现损伤之后,材料的弹性模量会出现退化,弹性模量的退化程度取决于等效塑性应变,拉压应力应变关系如下:
(20)

为了得到损伤演化规律,将式(20)变形为:
(21)
拉压应变εc和εt可以分解为弹性和非弹性应变的和:
(22)
(23)
d=1-(1-dt)(1-dc)
(24)
混凝土塑性损伤本构中参数主要有,弹性模量E0,泊松比v,抗压强度σcu,抗拉强度σtu,常数bt和bc。这些参数可以通过水泥砂浆室内单轴压缩试验与非计算均匀化方法的对比进行调试,细观组分的材料参数见表1,bt和bc分别取0.1和0.7。

表1 水泥砂浆细观组分的材料参数
室内试验和数值模拟的单轴压缩的应力-应变曲线见图10。从图中可以看出,数值模拟结果与室内试验结果整体比较吻合,但是由于实际中水泥砂浆中包含了初始裂纹和损伤,在弹性初始阶段会出现裂纹压密阶段,这个在塑性损伤本构关系中无法再现。另外由于是刚性试验机,材料达到抗压强度之后会突然破坏,导致下降段很陡。
图8中的非均匀材料用多尺度方法进行计算,其细观模型的材料参数见表1;均匀材料采用单一尺度模型进行计算,其本构关系也采用混凝土塑性损伤模型,材料参数取图10中的试验数据(虚线)。
4.3 结果分析
由于非线性计算均匀化方法不能处理非连续问题,将用渐进损伤过程来代替裂纹扩展路径的研究。由于计算均匀化方法的宏观本构模型是未知的,需要一个代表损伤的变量来研究渐进损伤过程。几何损伤理论认为[17],损伤模型应力的折减等于未损伤模型受力面积的折减。根据均匀化准则,宏观损伤因子可以表示为:
(25)
预裂纹倾角为45°的多尺度模型的损伤因子见图11。倾角为45°的试件的最终破坏模式见图12,可以看出数值模拟和室内试验的裂纹扩展路径相似。在数值模型中有2条反翼裂纹,而在室内试验中只有1条,主要原因是室内试验中的试件不是均匀的。不同地方的强度可能不一样,对应的细观结构也不一样,本文的非线性计算均匀化方法可以考虑不同的细观结构,但由于缺少细观结构的信息,所以只能暂时假定所有RVE结构都相同。虽然如此,数值计算结果与室内试验基本一致,说明非线性计算均匀化方法处理预裂纹扩展的适用性。模型中非均匀材料处的有限元单元用本文的多尺度模型进行计算时,每个增量步中每个单元高斯积分点的计算时间需要30 min左右,如果单元和增量步过多,模型加载完成需要数周;另外,如果某个单元对应的细观模型在某个增量步不收敛,将会导致整个多尺度模型的计算终止,因此本文的计算方法计算代价较大,需要在多尺度单元数量和计算代价间进行平衡,而且受细观模型的收敛性影响,需要注意选择更加容易收敛的细观本构模型。
不同原始裂隙倾角下的翼裂纹起裂角见表2。与室内试验结果相同,随着预裂纹倾角α的增大,翼裂纹起裂角逐渐减小,见图13,即翼裂纹向加载方向的偏转程度逐渐增大。

表2 不同原始裂隙倾角下的翼裂纹起裂角对比 单位:(°)
5 结论
本文提出了一种非线性计算均匀化方法,将非线性计算均匀化的一般步骤在ABAQUS中实现,并将其运用到非填充预裂纹扩展的多尺度模拟,得出以下结论。
a) 数值模拟和室内试验的单轴压缩应力—应变曲线拟合的很好,说明混凝土塑性损伤模型可以作为水泥砂浆等脆性材料的细观组分的本构模型。
b) 在预裂纹扩展数值算例中,不同倾角的裂纹的扩展路径与试验结果比较吻合,表明非线性计算均匀化方法在处理多尺度非线性问题是一个有效的方法,且用损伤来模拟裂纹扩展是可行的。
c) 随着原始裂隙倾角的增大,翼裂纹起裂角逐渐减小,即翼裂纹向加载方向的偏转程度逐渐增大。
