PA-DDS算法在新安江模型参数优化中的应用

余胜男，张雪，邵年华，吕海强

(1.深圳市广汇源环境水务有限公司，广东深圳518020；2.深圳市西丽水库管理处，广东深圳518050)

随着计算机技术的发展，洪水预报和水资源管理等众多领域开始逐渐借助流域水文模型进行预报和管理[1]。流域水文模拟旨在应用物理数学和水文学知识，在流域尺度范围内，对降雨径流过程进行局部或综合模拟，从而达到确定流域水文响应的目的[2]。目前国内外运用比较广泛的新安江模型，是20世纪60年代中国著名水文学家赵人俊教授提出的流域水文模型，该模型以蓄满产流为机制，适用于湿润地区或半湿润地区[3]。水文模型结构比较复杂，在参数优化过程中解集的选取存在计算效率和精度的矛盾[4]，参数优化方法主要包括试错法和自动率定法[5]，后者又包括局部寻优和全局寻优两种方法。局部寻优法可满足单峰函数解的要求，而对于复峰函数，则需通过全局寻优避免最优解限制于局部空间内[6]，所以全局优化算法更多的应用于多参数的水文模型参数率定中。

多目标优化算法[7]作为全局优化的重要组成部分，一般来说，多目标优化问题并不存在一个最优解，所有可能的解都成为非劣解，也称Pareto解，多目标优化目的在于搜寻可行的参数空间并找出其Pareto最优解集。目前广泛应用的多目标优化算法有NSGA-Ⅱ[8]法、AMALGAM法等。其中NSGA-Ⅱ算法因其解集分布广泛且均匀，寻优速度快的优点已经成为检验其他多目标寻优算法性能的参照标准。AMALGAM算法解的收敛性能较好，近年国内外学者也将其运用于数据大，模型结构复杂的参数优化中。PA-DDS算法作为新近提出的多目标优化算法，在求解过程中动态存档非劣解防止解的丢失，因此解集的广度及精度较高。国内对PA-DDS算法的应用研究[9-10]尚处于起步阶段，本文首次将其应用于多参数新安江模型参数优化中，且与NSGA-Ⅱ算法和AMALGAM算法在收敛性能和非劣解方面进行了对比，结合深圳西丽水库入库流量过程资料验证了该方法的优越性。

1 西丽水库概况

西丽水库(图1)位于深圳市南山区西丽街道境内，坝址位于珠江三角洲水系的大沙河上游河段右岸支流西丽水上。西丽水库控制流域面积29.0 km2，总库容4 000万m3，多年平均降雨量1 565 mm。水库于1959年动工兴建，原设计以防洪、灌溉为主，结合发电。随着经济的发展，西丽水库成为以防洪、城市供水为主[12]，兼具原水调蓄功能的中型水库,是供水网络干线(东部供水水源工程)末端的调节水库之一。水库担任着南山、宝安500万人口的供水任务，水库一旦失事，将影响居民的饮用水安全[11]。

西丽水库设有降雨、水位、蒸发自动观测站点。水位计于1997年建设，位于大坝右坝肩DN2200闸室旁，每隔15 min自动采集一个水位数据；雨量筒于2012年建设，位于西丽水库管理处办公楼楼顶，每隔15 min自动采集一个雨量数据；蒸发皿于2014年建设，位于大坝左坝肩背水坡，每日采集一个蒸发数据。

2 PA-DDS算法简介

存档动态维度搜索算法PA-DDS算法由动态维度搜索算法DDS发展而来，动态维度搜索(Dynamically Dimensioned Search, DDS[12])算法起始于全局搜索，即在全搜索域上产生初始解，随着迭代的进行，算法通过以服从正态分布的概率动态地减少解的变化维度实现搜索空间由全局向局部的转化过程，逐渐局限在一个局部空间内，最终求得目标函数最优解，但这种寻优过程容易出现将解丢失的情况。在动态维度搜索DDS算法的启发下且为避免该算法的弱点，Tolson和Asadzadeh结合Pareto存档进化策略(Pareto Archived Evolution Strategy, PAES)，提出了处理多目标问题的Pareto存档动态维度搜索(Pareto-Archived Dynamically Dimensioned Search, PA-DDS[13])算法，该算法能在搜索过程中动态存档所有非劣解，防止解的丢失，最终实现模型参数全局寻优。

PA-DDS方法的主要步骤(图2)为：①确定待解决的优化问题及其包含的目标函数，本研究选择的目标函数是相对误差及确定性系数；②采用DDS算法初始化种群，通过迭代寻优求解最优参数及最优函数值，并存档非劣解，形成Pareto前沿；③计算拥挤半径并据此找出步骤二中的Pareto前沿的最优解集；④设置扰动参数并对当前最优解集产生一定范围的扰动，重复步骤二，产生新的解集，若新解集为最优非劣解，则替代原解集，否则继续重复步骤二，直到找到最优非劣解且计算量达到设置的阈值为止。

3 优化过程

3.1 确定参数寻优空间

参数寻优空间由参数的上边界和下边界组成，可以根据人工经验法确定，也可以采用推荐的参数范围[14]。表1、2分别列出了日模型和次洪模型优化参数的上下边界。各参数意义如下：K为流域蒸散发折算系数；B为张力水蓄水容量曲线方次；C为深层蒸散发折算系数；Wm为流域平均张力水容量；Wum为上层张力水容量；Wlm为下层张力水容量；Im为不透水面积占全流域面积的比例；Ex为表层自由水蓄水容量曲线方次；Sm为表层自由水蓄水容量；Kg为表层自由水蓄水库对地下水的日出流系数；Ki为表层自由水对壤中流的日出流系数；Cg为地下水消退系数；Ci为壤中流消退系数；Cs为河网蓄水消退系数；X为马斯京根演算参数；KE为马斯京根法演算参数；L为滞时。

表1 日模型参数上下边界

注：KE=ΔT1，取时段间隔，L=0。

表2 次洪模型参数上下边界

3.2 目标函数

本文选择确定性系数和平均各场次洪峰相对误差作为目标函数，对应的方程分别是：

(1)

(2)

式中yoi、yci——实测流量和模拟流量序列；n——实测资料的长度。

4 应用实例

本文将PA-DDS算法收敛性能与NSGA-Ⅱ算法和AMALGAM算法进行对比，并将非劣解分布的均匀性及解的相似性方面与AMALGAM进行比较，选取深圳市西丽水库入库流量过程数据进行分析。

4.1 入库洪水还原计算

西丽水库无实测流量资料，实测的入库洪水过程可以采用水量平衡方程[15]进行计算：

(3)

上式可以写为

(4)

根据西丽水库逐日/时水位、降雨监测数据及引调水资料，根据式4可还原计算出等式左边数值即为日/次洪模型入库流量作为新安江模型的真值系列。

4.2算法收敛性能分析

基于超体积(Hyper-Volume)在评价Pareto前端收敛性、宽广性和均匀性时表现出来的客观性，常被用来评价多目标问题的搜索结果，本文选择超体积作为指标来判断PA-DDS算法与NSGA-Ⅱ算法和AMALGAM算法的求解质量，评价各种算法的收敛性能。其定义如下：

(5)

式中NPF——最终Pareto前沿上解的个数；νi——Pareto前沿上第i个解与参照点围成的体积。

对于目标函数最小的双目标优化问题，超体积值越大，表明Pareto前沿解集广度越大，因此可以采用超体积作为衡量算法所得非劣解集优劣性的判别标准。取西丽水库2014年入库洪水过程的新安江模型采用3种优化算法求目标函数最优解，并将求解过程中的迭代次数及计算超体积特征值绘制在图3中。从图3中可以看出，由于PA-DDS算法初始种群数量小于AMALGAM算法与NSGA-Ⅱ算法，所以在优化过程初期，PA-DDS算法超体积值略小，但PA-DDS算法达到收敛时的超体积值大于AMALGAM算法和NSGA-Ⅱ算法，表明其最终得到的解集广度更广且更加接近理论最优Pareto前沿，因此PA-DDS算法收敛性能较另外2种算法好。

4.3优化结果

4.3.1日模型优化结果

从图3中可以看出，PA-DDS算法和AMALGAM算法在达到收敛时两者对应的超体积值相对接近，所以将两种算法求解的目标函数值进行对比分析。选取2003—2013年共10 a的西丽水库实测入库流量过程作为日模型参数率定序列，将两种算法的Pareto前沿绘制在图4中。

由于PA-DDS算法在求解过程中会动态存储所有非劣解，所以其Pareto前沿的广度和均匀性要优于AMALGAM算法。同时在目标函数同时达到最小值的区域附近，PA-DDS算法非劣解分布更加密集且均匀，从图中可以看出来Pareto曲线为下凸曲线，有明显的拐点，从而满足获得最优解的条件，其算法表现相对更优。

将PA-DDS算法所得Pareto前沿下凸拐点时的参数组作为最优参数组，结果见表3。采用2014—2016年共3 a的资料用于参数检验。新安江模型日模平均相对误差为9.96%，平均确定性系数为0.75(表4)。本文罗列部分日模型实测及模拟过程线，见图5。

表3 日模型优化参数

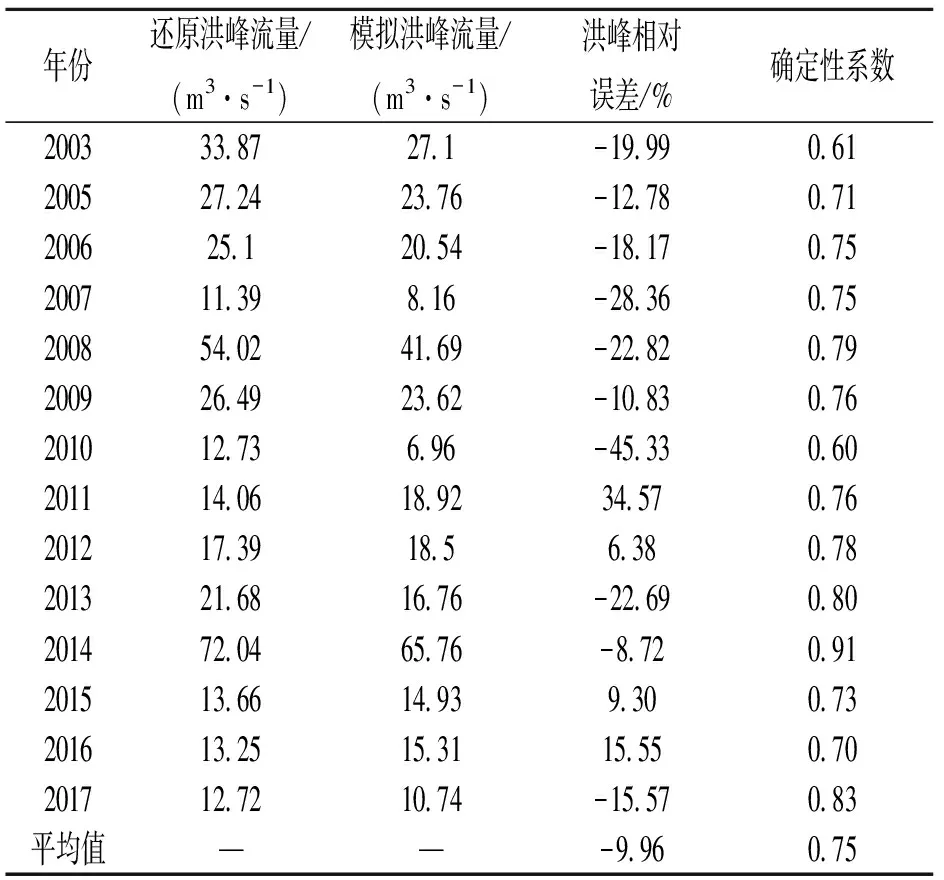
表4 日模型模拟效果

4.3.2次洪模型优化结果

选取40场洪水进行参数率定，10场洪水进行参数检验。将日模型最优参数组合中的K、B、C、Wm、Wum、Wlm、Im、Ex等8个参数直接运用在次洪模型中，次洪模型只需优化计算剩余的7个参数。将PA-DDS和AMALGAM两种算法的Pareto前沿绘制在图6中，从图中可以看出，2种算法的Pareto分布特点和图4相类似。将PA-DDS算法所得Pareto前沿下凸拐点时的参数组作为最优参数组，结果见表5。率定期和检验期洪水拟合精度统计情况见表6。从图7中可以看出，次洪模型模拟流量和实测流量拟合较好，平均确定性系数达到近0.84，部分确定性系数达到0.97。本文罗列部分次洪实测及模拟过程线，见图7。

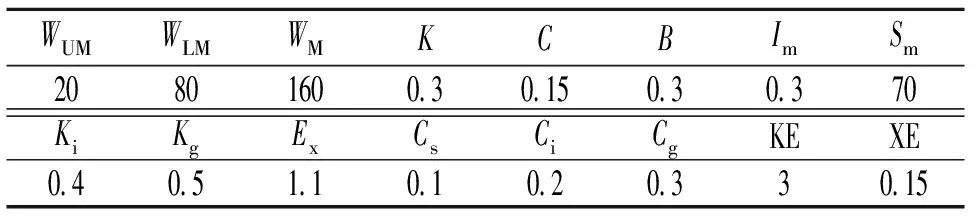
表5 次洪模型优化参数

表6 次洪模型模拟效果

5 结论

本文将PA-DDS 、NSGA-Ⅱ、AMALGAM 3种优化算法进行比较优选，优选结果表明，PA-DDS多目标优化算法在收敛性能方面优于NSGA-Ⅱ算法和AMALGAM算法，PA-DDS多目标优化算法在非劣解分布的均匀性及解的相似性方面优于AMALGAM。

本文首次利用多目标优化方法，采用PA-DDS算法对三水源新安江模型参数进行优化，以深圳市西丽水库入库流量过程资料进行分析，结果表明不论日模型和次洪模型，PA-DDS算法都表现出寻优速度快，非劣解分布范围广并且稳定等特点，表明PA-DDS针对新安江模型洪水预报这种多目标多参数优化中优势明显，并且模型模拟效果较好，可为西丽水库洪水预报模型提供技术支撑，为防洪与供水调度提供理论支撑，通过本文的应用实践，说明PA-DDS方法能够提高新安江模型的参数率定效率，为其参数优化提供新的思路方法，具有很好的借鉴意义，可以在其它流域推广应用。