基于Frenet坐标系和控制延时补偿的智能车辆路径跟踪

王威， 陈慧岩， 马建昊， 刘凯， 龚建伟

(北京理工大学 机械与车辆学院, 北京 100081)

0 引言

智能车辆是智能交通系统的重要环节，它能够有效减少交通事故、交通阻塞和环境污染等问题，也因此成为了近年来的研究热点[1]。运动控制是智能车辆的核心技术之一。所谓运动控制是指根据参考轨迹输入和控制律生成车辆执行器(如方向盘、电子油门、制动器、换挡机构等)的控制指令，产生影响车辆运动的力或力矩[2]，使车辆能够最终收敛于参考轨迹。

智能车辆运动控制包括速度控制和转向控制，二者存在耦合关系[3]。其中，转向控制与路径跟踪问题有关，即根据参考路径和车辆状态生成转向控制量，保证车辆稳定在参考路径上。目前常用的方法主要有纯跟踪算法、Stanley算法、前馈- 反馈控制器、线性二次型调节器和模型预测控制(MPC)等[4-6]。其中MPC控制器能够考虑车辆系统模型并对未来一段时间内系统的行为进行预测，通过求解带约束的最优控制问题，得到使预测时域内跟踪误差最小的最优控制序列[2]。同时，MPC控制器还具备较好的可扩展性，可以方便地应用在运动控制和运动规划中[7-8]。

由于传感器和执行器的数据传输和控制器数据处理占用时间，延时现象在智能车辆控制系统中是不可避免的。一般情况下延时的存在会引起控制器性能下降，甚至发生振荡[9-12]，影响智能车辆的稳定性和行驶安全性。为了解决控制延时对控制效果的影响，本文对转向控制延时进行建模，基于实车数据完成参数辨识并仿真获得等效的控制延时效果。之后，将转向控制延时加入到车辆运动模型并应用于MPC控制器，在Frenet坐标系下实现并验证算法的有效性。

1 基于Frenet坐标系的车辆运动模型

本文基于Frenet坐标系研究路径跟踪问题。对于智能车辆路径跟踪场景，可以忽略垂向运动，即将其简化为平面运动，此时Frenet坐标系指的是曲线切向量T，法向量N构成沿基准曲线移动的右手直角坐标系。该坐标系的特点是位置坐标(s,d)采用沿基线移动的切向距离s(即从基线起点开始走过的弧长)和法向位移d(即相对基线法向偏差)来描述，Frenet坐标系中的坐标(s,d)和笛卡尔坐标(x,y)可以通过基线坐标相互转化[13]。Frenet坐标系中曲线的切向量T和法向量N方向之间的关系如下[14]：

(1)

式中：κ为当前点的曲率。

为了在路径跟踪场景中应用Frenet坐标系，首先需要将笛卡尔坐标表示为弧长的向量值函数，即r(s)=x(s)i+y(s)j. 车辆在Frenet坐标系下t时刻的坐标可表示为

z(t)=r(s(t))+dN(s(t)).

(2)

假设车辆侧向速度为0，不考虑载荷转移，则Frenet坐标系下3自由度车辆运动学模型[15]为

(3)

式中：v为车辆绝对速度；φ为车辆相对于投影点的航向偏差，即φ=θ-θr，θ为车辆航向角，θr为路径航向角；κv和κr分别为车辆转向曲率和参考点曲率，对于阿克曼转向轮式车辆，忽略转向不足特性，有近似式κv=tanδ/L，δ为前轮转角，L为轴距。

Frenet坐标系下3自由度车辆动力学模型为

(4)

式中：vx和vy分别为车辆质心纵向和侧向速度；ω为车辆横摆角速度；ax为车辆质心纵向加速度；m为车辆总质量；Iz为车辆横摆转动惯量；lf和lb分别为质心到前后轴距离；Fy,f和Fy,b分别为前后轮侧向力，基于线性轮胎模型假设，有

(5)

Cf和Cb分别为前后轮侧偏刚度。

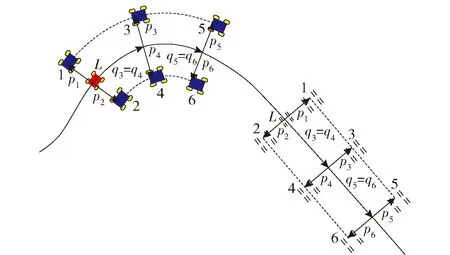
图1 Frenet坐标系下的编队行驶表述[16]Fig.1 A formation described by Frenet coordinates[16]

由上述可见，Frenet坐标可以直接表示车辆相对于参考路径的位置，相比之下，笛卡尔坐标系下表示这一相对位置需要在运动模型基础上进行误差模型推导。此外，Frenet坐标系下推导的车辆运动模型还可以直接用于多车编队行驶问题中，用以表示编队车辆相对于领航车的位置关系[16-17]。Frenet坐标系下的编队行驶表述如图1所示。

2 电控转向系统建模

2.1 电控转向系统

本文所用试验车辆为2006年款丰田陆地巡洋舰4700，其电控转向由加装在转向轴的无刷直流电机实现。具体实现方式是，电机控制器接收期望方向盘转角以及实际方向盘转角，产生梯形速度曲线，如图2所示。

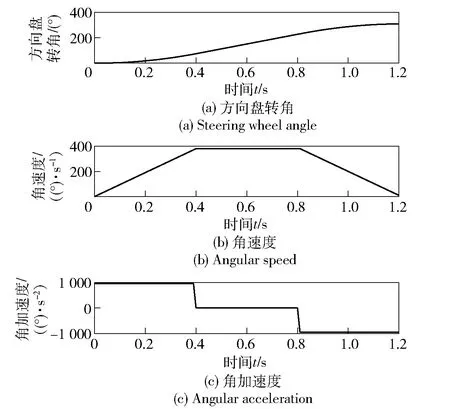
图2 电控转向控制效果示意图Fig.2 Electronic steering control performance

假设方向盘转角δw与前轮转角δ为线性关系，即δw=kδ，其中k为传动比。经过理论推导和实车测试验证，该试验平台的转向系统性能及约束如表1所示。

表1 试验车辆转向系统性能及约束(k=18.57)

2.2 基于实车数据的转向延时模型

在实车测试过程中发现，电控转向存在一个较大的延时，期望前轮转角曲线和实际前轮转角曲线时间相位相差近1 s，因此必须对延时建立模型以获得更好的跟踪精度。

国内外一些学者对车辆电控系统的延时问题进行了研究[10-12,18]。其中：文献[18]研究的问题是纵向速度控制，将加速度表述为1阶惯性延时模型；文献[11-12]研究的问题则是4轮独立驱动车辆的横摆角速度控制问题，将横摆力矩表述为纯滞后和1阶惯性延时的串联结构模型；文献[10]基于TORCS赛车仿真环境研究了智能车辆转向控制延时问题，其核心思想是预测延时时间内跟踪误差的变化，并基于预测值计算转向控制量。本文考虑将前轮转角表述为纯滞后和1阶惯性延时的串联结构模型(如图3所示，其中δe(t)为t时刻车辆期望前轮转角)，并在Simulink中搭建仿真模型，以实车测试中MPC计算得到的期望前轮转角序列作为模型的输入，估计实车测试过程中实际前轮转角的响应曲线，以实车测试数据为对比基准，优化仿真系统参数，解决如下优化问题：

(6)

式中：‖·‖2表示取2范数；是指延时模型预测的实际前轮转角序列；δr是指实车测量的实际前轮转角序列；τ1是1阶惯性时间常数；τp是纯滞后时间。

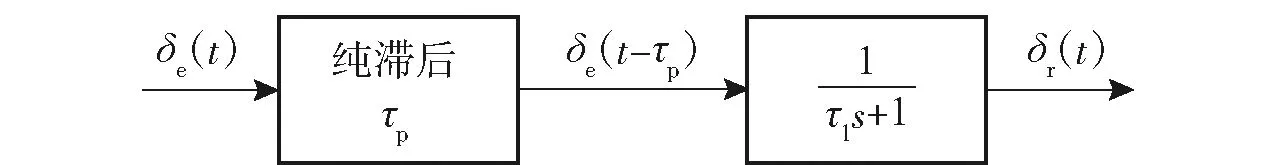
图3 转向控制延时模型Fig.3 Electric steering control delay model

优化结果如表2及图4所示(其中δf为车辆预测前轮偏角)。除启动阶段(t<2.0 s，期望前轮转角和实际前轮转角差值超过10°)延时模型的预测效果较差之外，后续预测效果非常接近实车数据，则电控转向系统的模型可以表示为

(7)

表2 延时模型优化结果

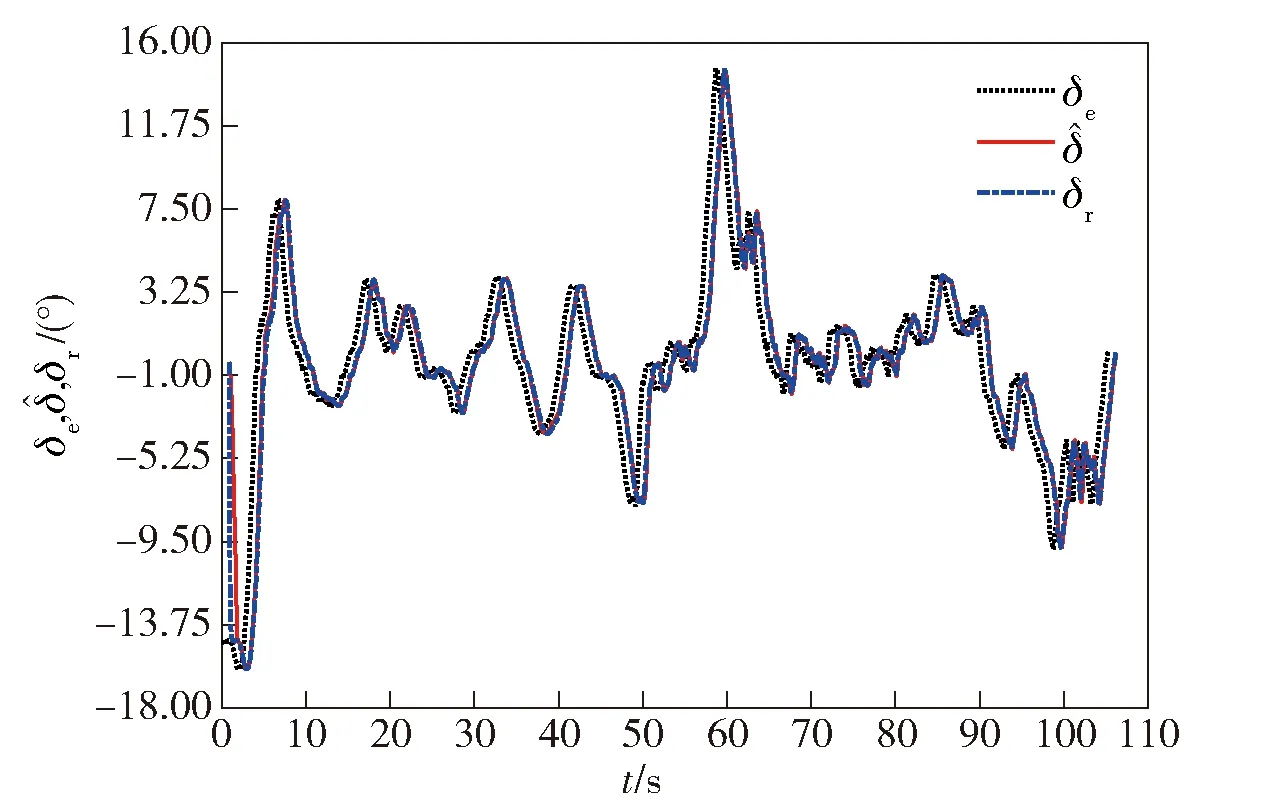
图4 延时模型优化辨识结果对比Fig.4 Comparison of expected, actual and predicted front wheel angles

2.3 仿真模拟

为了能够更方便地研究延时模型，本文在V-REP中基于Lincoln MKZ车型(详细参数见4.1节)搭建仿真车辆平台，在仿真环境中建立等效的延时模型。系统框架如图5所示。

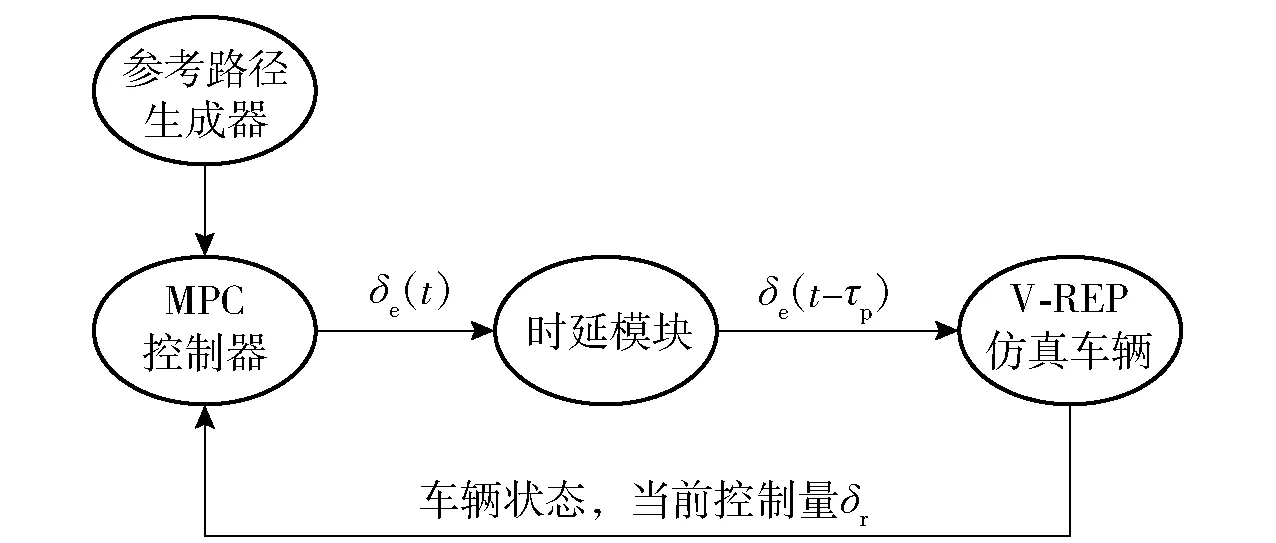
图5 基于V-REP和ROS的仿真环境Fig.5 Simulation environment based on V-REP and ROS

提取仿真数据中的期望前轮转角作为上述延时模型的输入，将输出作为下一时刻实际前轮转角的预测值，并与仿真测试的实际前轮转角进行对比如表3及图6所示。从中可以看到，仿真环境中的转向系统延时同样适用于上述模型，即在仿真中成功建立了等效的延时模型。下面将基于该仿真环境对存在延时的路径跟踪控制算法进行研究与测试。

表3 仿真环境控制量预测效果

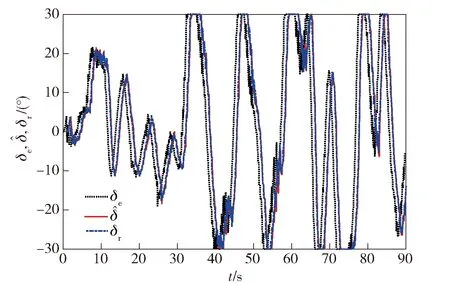
图6 仿真环境延时模型预测结果Fig.6 Predicted result of delayed control model in simulation

3 基于Frenet坐标系的MPC路径跟踪算法

3.1 不考虑控制延时的MPC路径跟踪算法

对于运动学MPC，将(3)式作为参考模型，对其进行离散化：

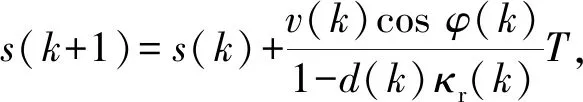
(8)

式中：T为MPC控制器采样周期。

设z=(s,d,φ)T为状态量，u=δ为控制量，假设车速v为定值。

对于动力学MPC，将(4)式和(5)式作为参考模型，离散化得

s(k+1)=s(k)+λ(k)T，
d(k+1)=[vx(k)sinφ(k)+vy(k)cosφ(k)]T，
φ(k+1)=ω(k)-λ(k)κr(k)，
vx(k+1)=vy(k)ω(k)+ax(k)，
vy(k+1)=-vx(k)ω(k)+[Fy,f(k)+Fy,b(k)]/m，
ω(k+1)=[lfFy,f(k)-lbFy,b(k)]/Iz，

(9)

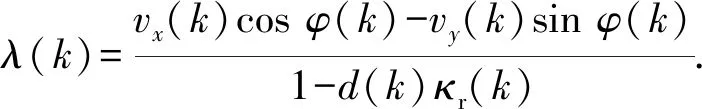
状态量变为z=(s,d,φ,vx,vy,ω)T，控制量仍为u=δ，模型中假设ax为0. 代价函数为

(10)

式中：wd、wφ、wu、wdu分别为横向跟踪误差、航向角误差、转向控制量、转向控制量变化率代价项的权重系数，本文中设置为[wd,wφ,wu,wdu]=[1,8,1,1 000]；Np为预测时域内的离散状态数量。

则路径跟踪问题可以表述为如下优化问题：

(11)

式中：f(z,u)表示采用的车辆运动模型；δmax为前轮转角最大值.

3.2 考虑控制延时的MPC路径跟踪算法

采用前述基于Frenet坐标系的车辆运动学模型，同时考虑转向系统控制模型，对(7)式进行离散化处理：

(12)

此时，将前轮转角作为状态量，期望前轮转角作为控制量，对于运动学模型，状态量变为z=(s,d,φ,δ)T，控制量变为u=δe；对于动力学模型，状态量变为z=(s,d,φ,vx,vy,ω,δ)T，控制量变为u=δe. 代价函数不变，优化问题的约束增加对期望前轮转角的约束：

|δe|≤δmax.

(13)

对于1阶惯性延时，在MPC参考模型中已经考虑，但是纯滞后延时意味着MPC计算得到的期望前轮转角经过τp时间后才可得到执行。因此，在MPC求解之前，首先基于历史期望前轮转角数据对车辆状态进行采样预测，将预测得到的状态作为MPC输入的初始状态，流程图如图7所示。

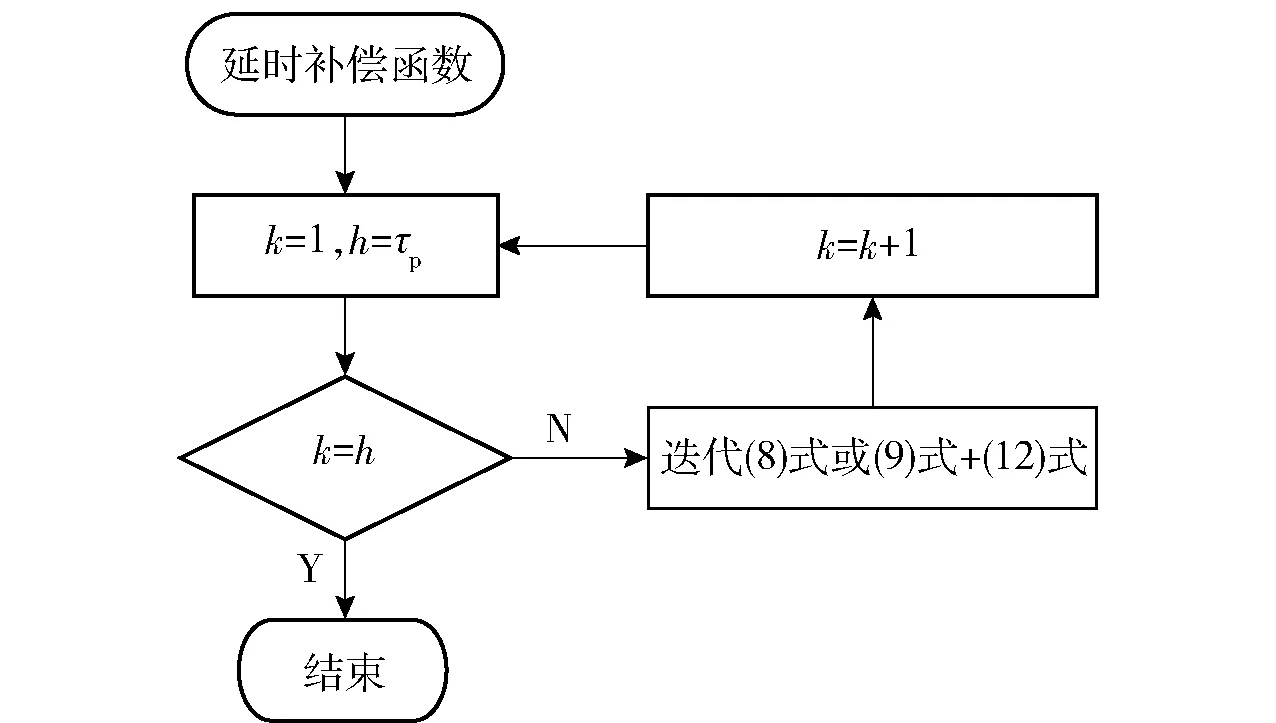
图7 延时补偿流程图Fig.7 Electric steering control strategy

4 仿真实验与分析

4.1 仿真环境搭建

本文基于ROS[19]和V-REP[20]搭建仿真验证平台(如图8、图9所示)，该平台的优势在于：一方面，ROS是一个基于消息通信的分布式进程框架，拥有庞大的基础库和可视化调试工具，可快速搭建系统原型、快速实现算法开发和验证；另一方面，V-REP拥有多种物理引擎以及用户与场景实时交互的能力，并设有ROS通信接口，可以快速部署V-REP与ROS的联合测试[21]。尽管V-REP存在运算资源占有率高[22]和构建复杂动力学模型难度较大的问题，但是通过配置高性能计算机，以及基于实车试验数据构建车辆近似模型，V-REP可以作为算法验证的理想环境。

图8 VREP仿真环境Fig.8 VREP simulation environment

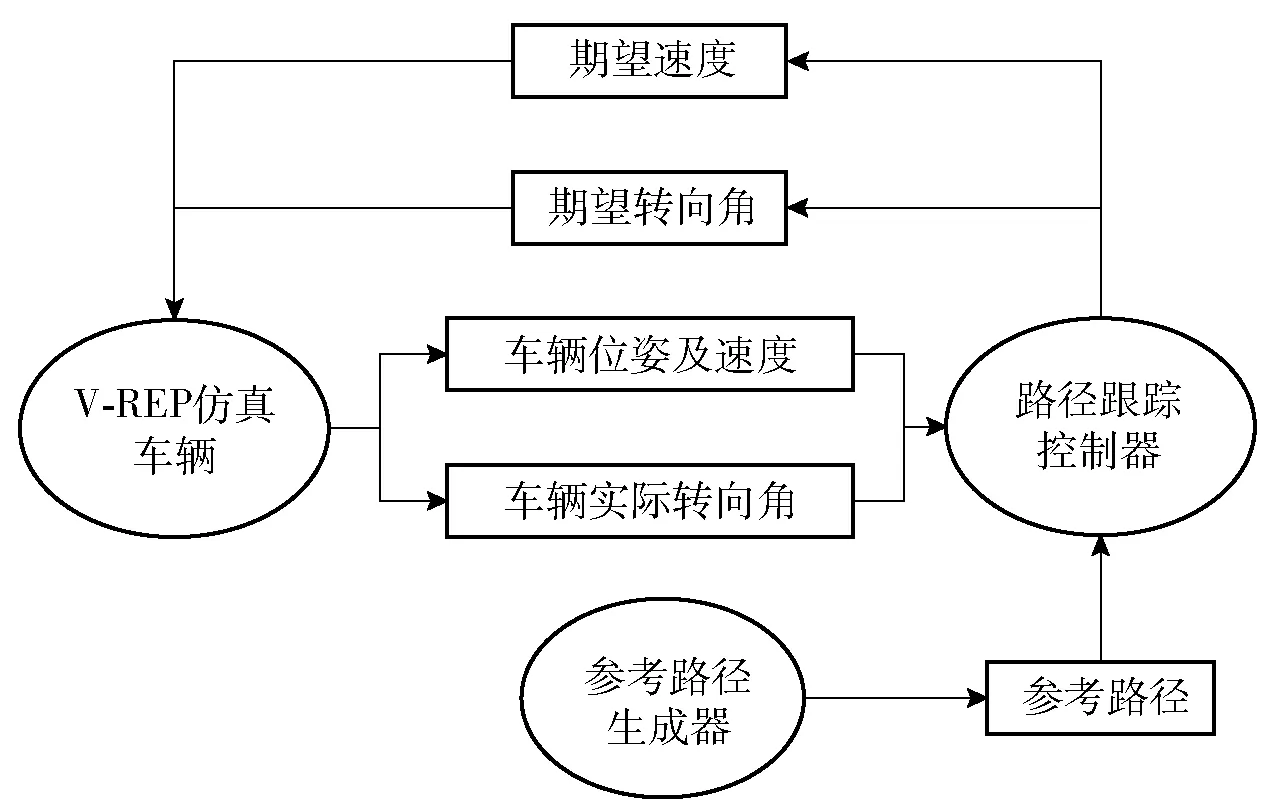
图9 ROS节点及消息示意图(椭圆代表ROS节点，矩形框代表节点发布和订阅话题的消息内容)Fig.9 ROS nodes and messages diagram (ellipse represents ROS node, and rectangle represents ROS message published and subscribed in a relative topic)

本文仿真环境设置和硬件配置如下：V-REP完成场景和车辆模型搭建和仿真；MPC控制器封装为ROS节点，作为仿真车辆的路径跟踪控制器；全局路径生成器用来采集和发布参考路径；采用官方推荐的ROSInterface方案实现V-REP与MPC控制器之间的通信。上述MPC控制器在安装Ubuntu 16.04 LTS系统的PC机上采用c++语言实现，PC机使用CPU型号Intel i7-7700HQ 2.80 GHz，内存16 GB. 选择非线性求解器Ipopt作为MPC优化问题的求解器。仿真车辆选择Lincoln MKZ，其参数如表4所示。

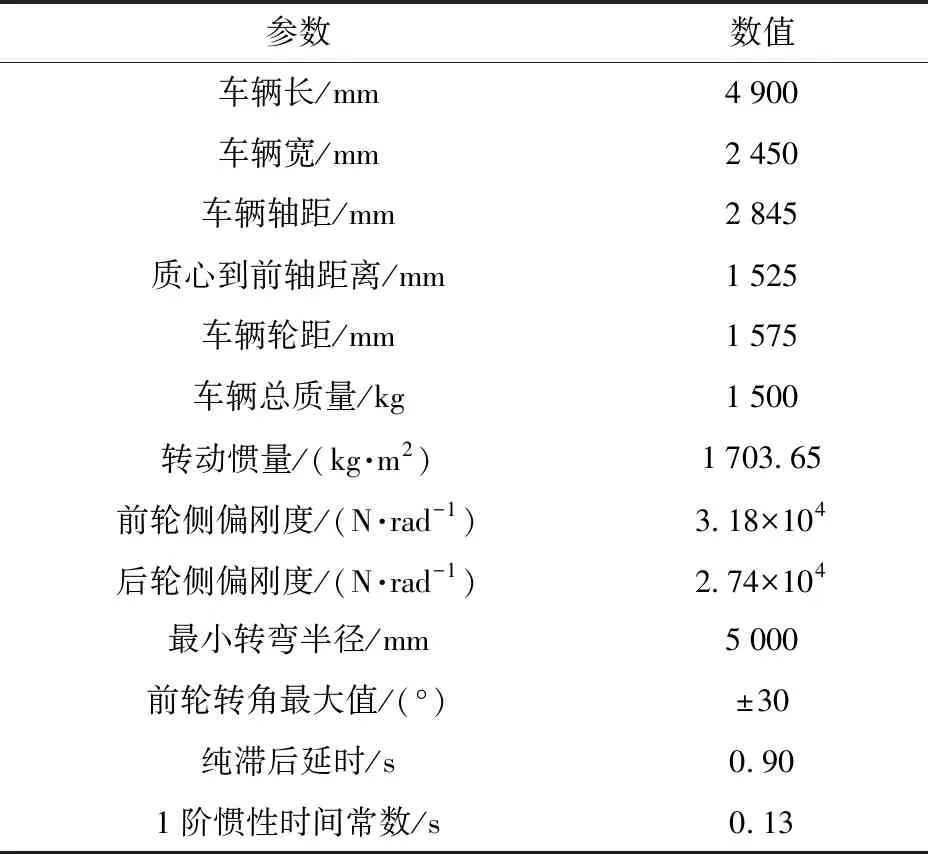
表4 仿真车辆参数

为了充分验证上述算法在不同速度工况下对变曲率及大曲率路段的跟踪效果，通过人工驾驶仿真车辆的方式以3种车速工况采集参考路径，路径形状和基本特征统计如图10及表5所示。

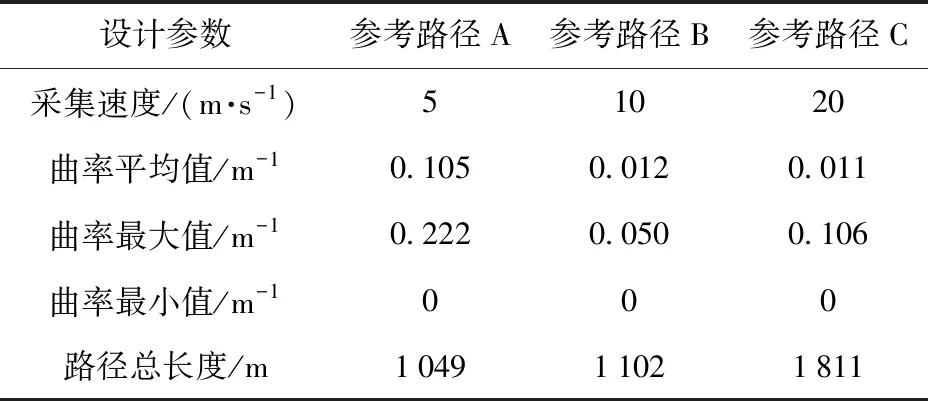
表5 参考路径设计参数

图10 全局参考路径Fig.10 Global reference path

4.2 不考虑控制延时的MPC路径跟踪实验

首先考察系统无延时情况下，基于Frenet坐标系的MPC路径跟踪控制效果。车辆速度设置与人工采集速度相同，参考路径A、B、C的跟踪速度分别设置为5 m/s、10 m/s、20 m/s. 跟踪控制效果如图11及表6所示。从中可以看到，对于存在连续变曲率和大曲率路段的参考路径，采用与人工驾驶相近的车速工况，本文所设计的MPC路径跟踪控制器取得了很好的跟踪效果。

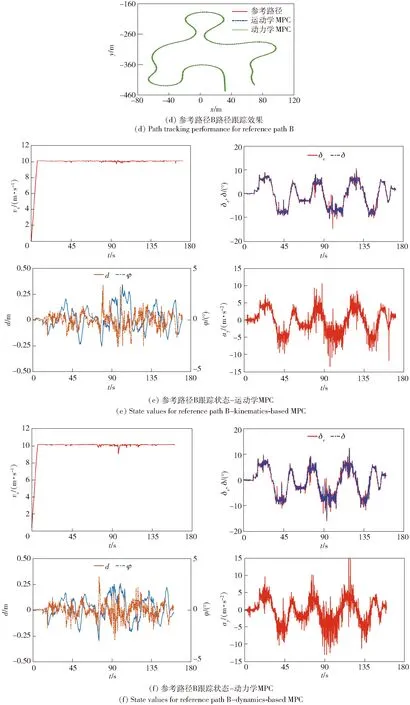
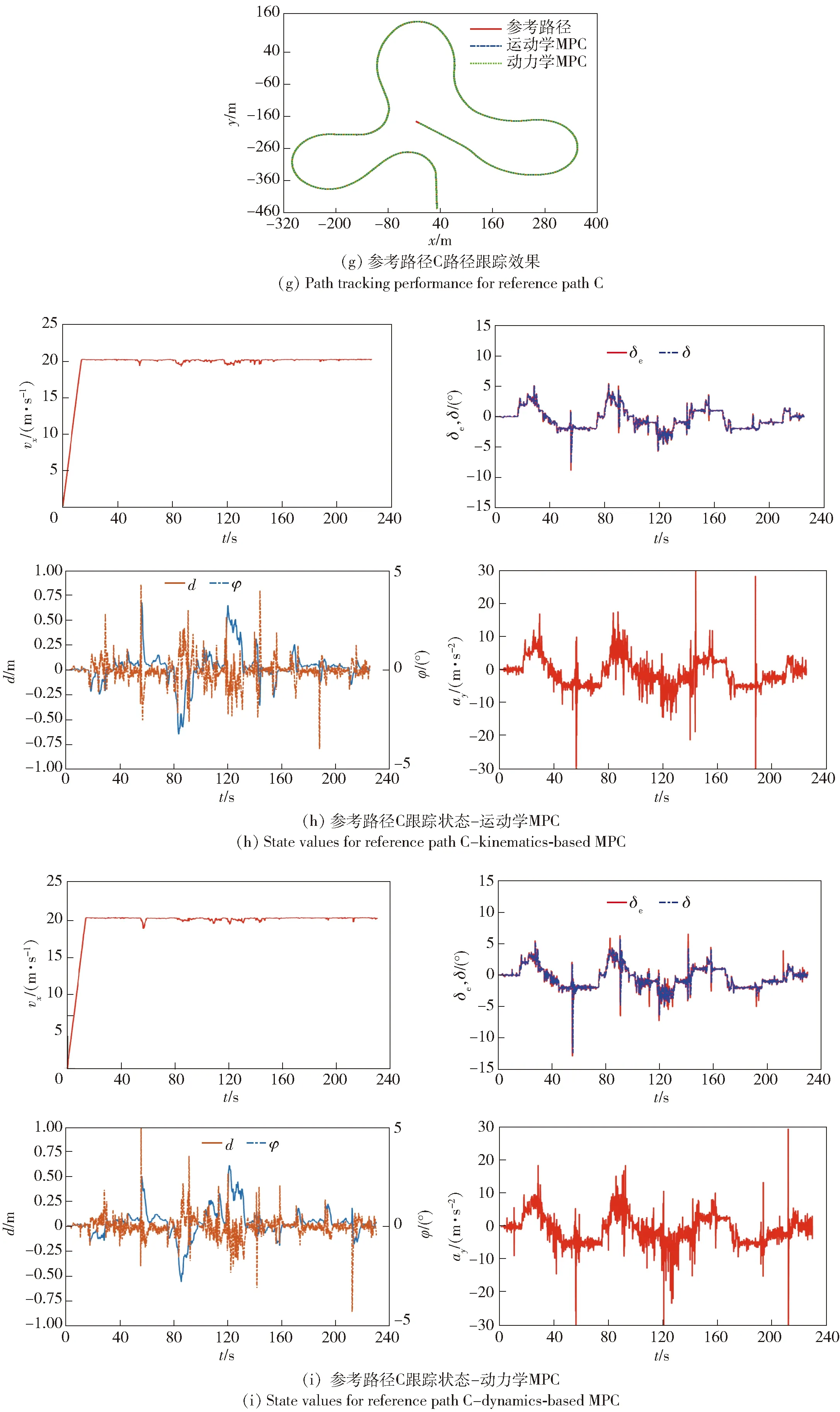
图11 系统不存在延时情况下的跟踪效果图Fig.11 Tracking performances without delayed control inputs

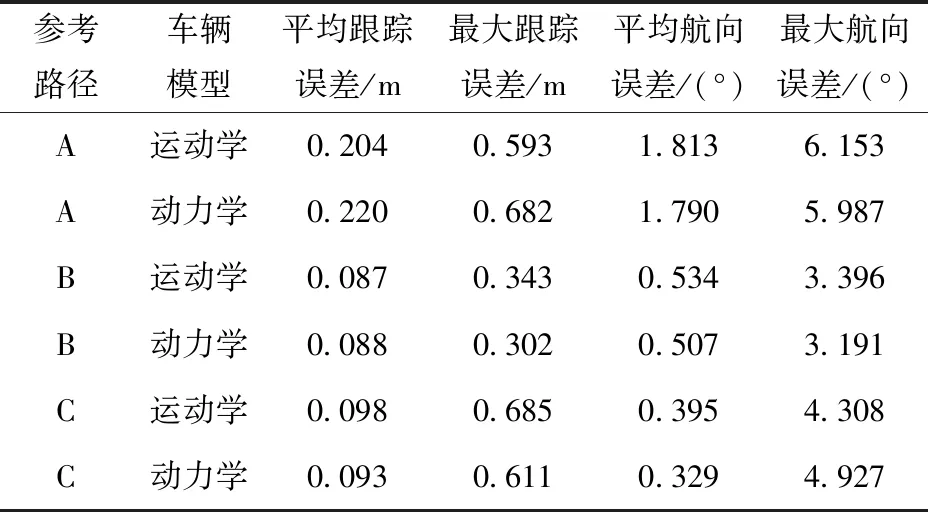
表6 系统无延时情况下的跟踪效果

4.3 考虑控制延时的MPC路径跟踪低速实验

首先考察5 m/s车速对参考路径A的跟踪效果。在系统存在控制延时的情况下，对比有无控制延时模型的跟踪控制效果，以及所用延时参数对跟踪效果的影响，实验结果按照平均跟踪误差升序，如表7所示。从中可以看到：1)在使用延时模型的情况下，跟踪效果基本都能好过使用相同车辆模型、不考虑控制延时的MPC控制器，特别是在最大跟踪误差和航向偏差指标上提升较多，但如果延时参数设置不当会更差；2)延时参数设置为辨识结果的跟踪效果最佳，对于运动学MPC，相比不考虑延时模型得到了较大提升，平均跟踪误差降低了83.7%，最大跟踪误差降低了74.4%. 由此验证了在MPC路径跟踪控制器中应用本文所述控制延时模型的有效性。

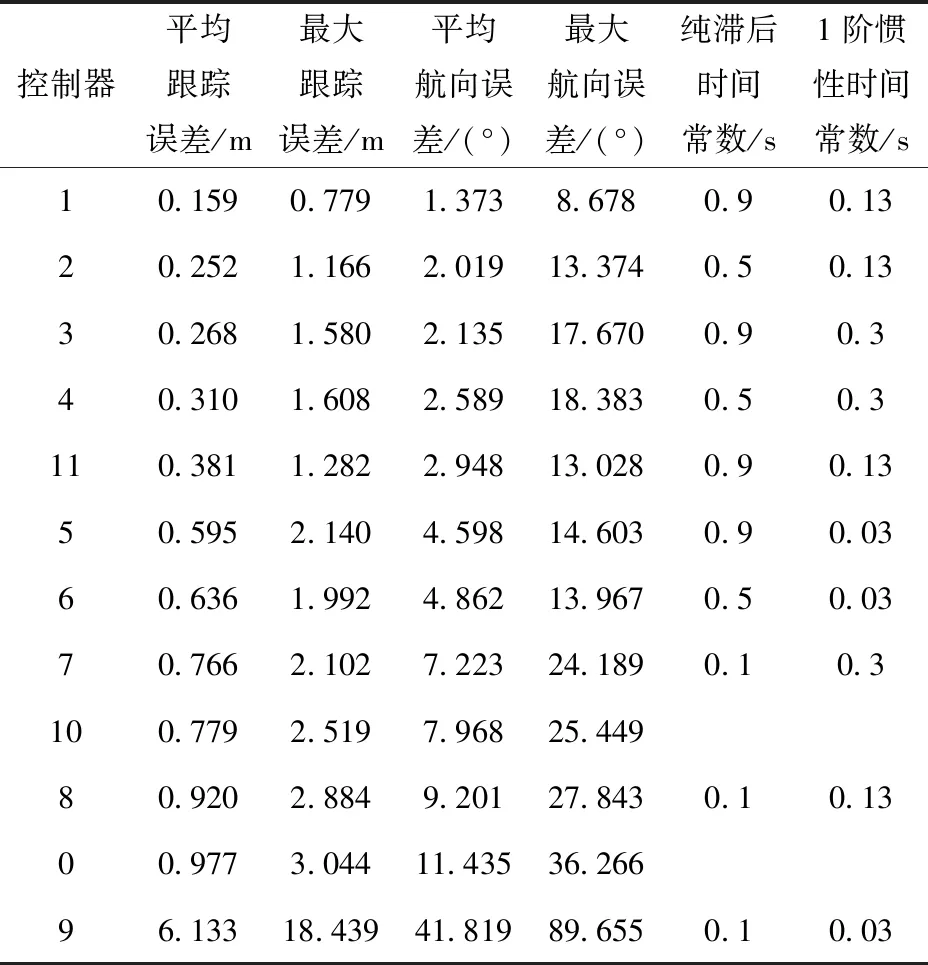
表7 系统存在延时情况下的跟踪效果(5 m/s)

注：控制器0为无延时模型的MPC控制器；控制器1～9均为有延时模型的运动学MPC控制器；控制器10和控制器11分别为无/有延时模型的动力学MPC控制器；控制器9效果发散，无法跑完全程。

图12对比展示控制器0、控制器1、控制器10、控制器11的跟踪效果总览和状态量。

4.4 考虑控制延时的MPC路径跟踪高速实验

为了进一步验证算法在高速工况下的效果，针对参考路径B和C继续开展实验。根据参考路径A低速实验场景的实验结果，这里只选择控制器0、控制器1、控制器10、控制器11进行实验。

首先是参考路径B，车速设置为10 m/s，在系统存在控制延时的情况下进行对比测试。4个控制器除了不考虑延时的运动学MPC(控制器0)在通过第一个弯道之后便振荡至侧翻之外，其余3个均安全跑完全程。从表8统计结果及图13对比效果来看，考虑延时的MPC控制器在航向偏差和最大跟踪误差指标上表现优异，其中控制器11相比控制器10分别有约70%和18%的提升。值得注意的是，不考虑延时的动力学MPC(控制器10)在0.9 s控制响应延时影响下仍然能够保持较高的稳定性和跟踪精度，而考虑延时的动力学MPC(控制器11)相比之下在平均跟踪误差指标上反而表现更差。分析状态曲线推测原因为，动力学模型需要更多的车辆状态量反馈，特别是侧向速度、横摆角速度等涉及侧向运动的状态量，相比运动学模型对噪声更加敏感，这会引起对预测车辆状态的更多干扰。

在车速设置为20 m/s的参考路径C试验中，如果完全按照实车延时效果设置系统仿真，会导致所有控制器在弯道处发生振荡至侧翻，无法跑完全程，因此设置低延时仿真实验，响应延时改为0.3 s，同时将纯滞后延时修改为0.3 s. 此外，由于参考轨迹是人工驾驶以接近极限工况的状态采集的，因此为了稳定车辆在延时系统下的控制量，增加了前轮转角变化量约束|Δδ|≤0.1 rad. 仍然对上述4种控制器进行对比实验，由图14及表9发现只有考虑延时的动力学MPC控制器可以安全跑完全程，其余3个控制器均在同一地点发生了侧翻。这个结果进一步体现了动力学模型在高速工况下的优势，同时也进一步验证了本文构建的延时模型有效性。

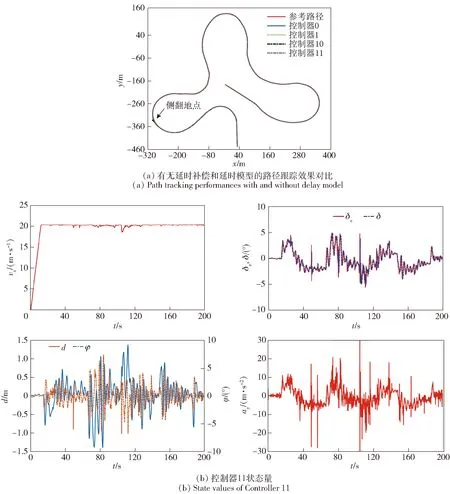
图14 系统存在延时情况下的跟踪效果图(20 m/s)Fig.14 Tracking performances with delayed control inputs (20 m/s)

表9 系统存在延时情况下的跟踪效果(20 m/s)

4.5 计算耗时分析

最后，对本文涉及仿真实验中4种控制器(控制器0、控制器1、控制器10、控制器11)计算耗时进行统计分析，如图15所示。控制器的运行周期设置为50 ms，在使用非线性优化的情况下，运动学MPC(控制器0和控制器1)在运行周期内可以完成计算得到控制量，动力学MPC(控制器10和控制器11)绝大部分情况能够在50 ms内运算完成。

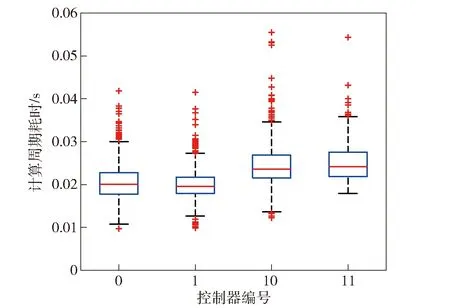
图15 计算耗时Fig.15 Computation Cost

5 结论

1)本文对智能车辆路径跟踪问题中存在的控制延时问题开展了研究。通过V-REP和ROS搭建了与实车转向延时特性等效的仿真车辆模型，并在Frenet坐标系下基于运动学和动力学模型构建了不考虑和考虑控制延时两种MPC路径跟踪控制器。

2)在5 m/s、10 m/s、20 m/s车速下的无延时车辆系统路径跟踪实验中，不考虑控制延时的MPC控制器获得了平均跟踪误差低于0.22 m的控制效果；而大延时车辆系统路径跟踪实验表明，考虑控制延时的MPC控制器相比不考虑控制延时的MPC控制器取得了较大的效果提升，特别是在最大跟踪误差和航向误差指标上表现优异，平均跟踪误差降低了83.7%，最大跟踪误差降低了74.4%.

3)通过分析实验结果发现，对于高延时系统，低速工况下考虑延时的运动学MPC表现更好，而高速工况下动力学MPC表现出了更加稳定的跟踪性能。特别地，在20 m/s车速下的低延时实验中，仅考虑控制延时的动力学MPC控制器安全地跑完了全程，进一步验证了动力学模型和延时模型在高速工况下的优势。