基于CFD-DEM法的矩形喷动床与柱锥形喷动床颗粒喷动特性模拟
2019-12-21宋海萍高亚平王瑞芳
雷 琨,宋海萍,高亚平,徐 庆, ,吴 龙, ,王瑞芳,
(1. 天津科技大学机械工程学院,天津 300222;2. 低碳绿色过程装备国际联合研究中心,天津 300222)
微波喷动床是集微波加热与喷动床优势于一体的微波联合干燥装置.其既具有微波加热速度快的优点,又能利用喷动床中物料的随机运动改善微波加热不均匀性的缺点.传统喷动床为柱锥形结构,但在微波喷动床结构设计时,为了保证喷动床内电磁场分布均匀性,矩形腔更适合于微波均匀加热.本文作者已在前期基于电场分布均匀性对单馈口矩形微波喷动床结构进行了设计[1],采用多物理场软件COMSOL Multiphysics 模拟研究了喷动床内部的电场分布情况,得到电场强度大且电场分布均匀的单馈口矩形微波喷动床结构,其长×宽×高为427 mm×427 mm×1 000 mm.针对该结构,本文采用离散元气固耦合法(CFD-DEM)对矩形喷动床内小麦颗粒喷动特性进行模拟研究.
CFD-DEM 法可以同时模拟研究流场和颗粒的动力学行为,包括流场和颗粒本身的动力学特性以及流场与颗粒相互作用的动力学特性,其研究结果更具可靠性和真实性.近年来,CFD-DEM 法被越来越多地应用于流态化技术方面研究,黎明等[2]通过CFDDEM 法模拟了流化床的工作机理;Kafui 等[3]采用CFD-DEM 法模拟了颗粒在流化床内的流动特性;匡世波[4]开发了三维CFD-DEM 软件,并利用该软件预测了气力输送过程;田凤国[5]通过数值模拟对内循环流化床气固两相流进行了数值模拟,得出颗粒流动规律.Khawaja[6]通过CFD-DEM 法对流化床内的声波与颗粒流化的影响进行了研究,并得出系统中的阻尼受固相黏度的影响.Kerst 等[7]利用CFD-DEM 法对流化床内结晶水的流化特性进行研究,证明了流化床内结晶水流化特性简化模型的可靠性.Fries 等[8]用CFD-DEM 法对喷雾造粒在流化床中物性变化进行研究,结果表明不同喷雾方式及不同材料对喷雾造粒过程都会产生很大的影响.Ebrahimi 等[9]通过CFDDEM 法研究大型喷动流化床的喷动特性,提出一种缩放方法,既可以减少计算时间又可以保证计算的精确性.Sutkar 等[10]用CFD-DEM 法研究液态喷射对喷动流化床内颗粒与液滴之间的相互作用以及喷动流化特性的影响,并得到了物料水分的分布情况.Salikov 等[11]通过CFD-DEM 法研究了菱形喷动床内气流对喷动稳定性的影响,在进口气速和压降等方面都与实验保持了一致性.Liu 等[12]用CFD-DEM法对喷动床内的高密度核燃料颗粒在不同密度下颗粒的床层表现进行研究,得出了颗粒在喷动床中的最小喷动速度、进气速度、稳定喷动速度、压降以及燃料涂层随颗粒密度的变化.
传统的柱锥形喷动床结构方面的设计理论与经验相对成熟,而矩形喷动床的相关研究则较少.本文通过将矩形喷动床与柱锥形喷动床在混合时间、单颗粒循环时间、颗粒运动及气体压力(表压)等方面进行对比,探索矩形喷动床喷动特性的优缺点,以便对其结构进行改进.
1 数学模型
在流固耦合系统中,连续的流体相与离散颗粒相之间相互影响,在建立模型时要采用双向耦合的方法处理两相间的相互作用.CFD-DEM 模型用欧拉方法描述流体相和离散颗粒相的运动.该模型中,流体运动用两相耦合的Navier-Stokes 方程描述,即在单相Navier-Stokes 方程中加入空隙率以及动量交换源项;颗粒的运动则考虑颗粒间相互碰撞作用力以及流体对颗粒的作用力,通过直接跟踪颗粒的运动轨迹进行描述.
1.1 气固耦合流体动力学控制方程
流体在单独流动的过程中要遵循三大守恒定律,即质量守恒定律、动量守恒定律和能量守恒定律,其控制方程是三大守恒定律的不同形式的表达.CFDDEM 耦合时存在颗粒相,因此在流体动力学研究过程中要考虑空隙率的影响,其方程一般的通用形式为
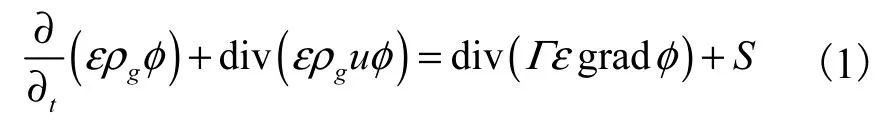
式(1)中从左至右依次是瞬态项、对流项、扩散项、源项[13],其展开形式为
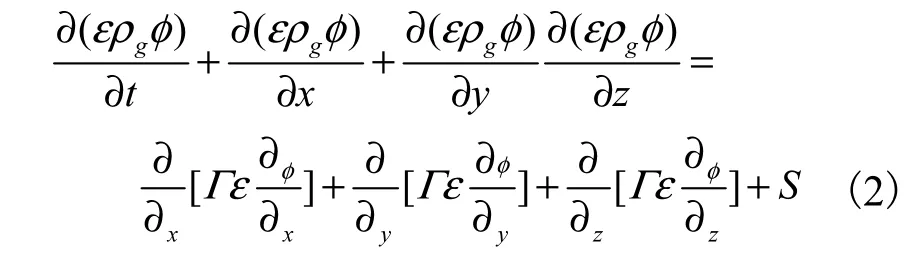
式中:ε 为空隙率;φ 为通用变量;Γ 为广义扩散系;S为广义源项.
表1 给出了控制方程中φ、Γ 和S 与每种特定方程的对应关系.

表1 通用控制方程中各符号的表达式 Tab. 1 Expressions of symbols in general governing equation
1.2 气体与颗粒的作用力方程
气体与颗粒之间存在浮力、压力梯度力、曳力、Magnus 力、Basset 力、Saffman 力等多种类型相互作用力.但对于密相颗粒或者无黏性的干颗粒,且颗粒密度远大于气体密度时,与曳力相比,其他作用力均较小,可忽略.因此在计算颗粒与气体之间存在的双向耦合力时,可以只考虑曳力作用.单颗粒上受气体作用力[14]为
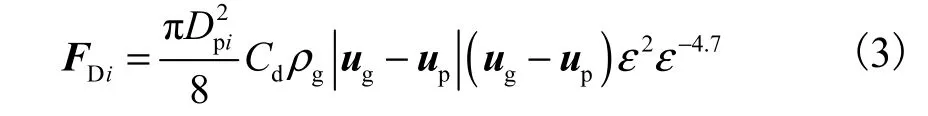
式中: FDi为当前时步单颗粒i 所受的气体作用力;为颗粒i 的等效直径;ρg为气体密度;ug为颗粒i 所在网格的气体速度,可通过求解气固耦合的气相控制方程求出;up为当前时步颗粒i 的运动速度,可由CFD-DEM 耦合计算求出;ε 为空隙率,即网格内气体所占体积的百分比;Cd为单颗粒曳力系数(颗粒阻力系数).
1.3 接触模型
颗粒的接触模型采用Hertz-Mindlin 无滑移接触模型,该模型可以准确地计算出两个颗粒在弹性接触时的接触作用力.
设两球形颗粒发生碰撞接触,其法向叠合量为

式中:R1、R2分别为两球形颗粒的半径;r1、r2分别为两球心的位置矢量.
合力和合力矩通过颗粒碰撞过程中切向接触力和法向接触力的叠加来计算.颗粒间的法向接触力

其中

式中: E*为等效弹性模量;E1、E2分别为两颗粒的弹性模量;R*为等效粒子半径;分别为两颗粒的泊松比.
颗粒间的切向接触力

其中

式中:St为切向刚度;δ 为切向叠合量;G*=,为等效剪切模量,其中G1、G2分别为两颗粒的剪切弹性模量.
2 几何体模型和颗粒模型
矩形喷动床与柱锥形喷动床的几何体模型见图1,计算域为三维空间.小麦颗粒采用球形颗粒模型,由于小麦颗粒为不规则形状,且接近椭圆形,因此在测量时采用了等球平均粒径.几何体与物料相关参数及模型参数见表2.

图1 矩形喷动床与柱锥形喷动床模型 Fig. 1 Model of rectangular spouted bed and cylindrical spouted bed

表2 模型参数 Tab. 2 Parameters of the model
3 结果与讨论
3.1 模型验证
为验证CFD-DEM 耦合模型用于分析矩形喷动床喷动特性的正确性与可靠性,作者对前期设计的长、宽均为 300 mm、高为 800 mm,床层高度为120 mm 的矩形喷动床[17]进行了模拟,并将利用本模型模拟得到的最小喷动速度、循环时间和完全混合时间等参数与文献[17-19]的数据进行对比分析.
3.1.1 最小喷动速度对比
最小喷动速度实验结果[17]与本文模型模拟的最小喷动速度结果对比见图2.最小喷动速度分别为0.17 m/s(文献)和0.14 m/s(模拟),模拟值与实验值相差17.6%,吻合度较好.

图2 最小喷动速度对比 Fig. 2 Comparison of the minimum spouting velocity
最小喷动速度通常也用Mathur-Gishler 提出的经验公式[20]确定,用此经验公式计算的结果为0.15 m/s,模拟值与经验公式计算值相差7.1%,具有较好的吻合度.
3.1.2 单颗粒循环时间对比
将颗粒从喷动床某一高度出发后经过一个循环(即颗粒经过环流区、喷动区和喷泉区)再次回到该高度的时间定义为单颗粒循环时间.模拟得到的单颗粒循环时间为1.85 s,模拟结果与Luo 等[18]得到的矩形喷动床内单颗粒循环时间0~2.5 s 吻合.
3.1.3 混合时间对比
颗粒在喷动床内达到完全混合的时间也是表征喷动床喷动效果的因素.混合时间主要通过混合指数判断.将颗粒标定为两种不同颜色,并等量分为上下两层放置于矩形喷动床中.模拟结束后,取出一定量的颗粒,计算其中一种颜色颗粒的质量占总颗粒质量的质量分数,将其定义为混合指数M.当混合指数为0.5 时认为混合达到均匀.
模拟中,混合时间为5.2 s 时混合指数达到0.5,说明颗粒已经混合均匀(图3).王喆[17]的研究表明,虽然有一定的波动性,但是当混合时间为6 s 时,颗粒基本混合均匀,此结果与本文模拟结果吻合.朱润儒[19]的研究发现,经过7 s 后颗粒达到了充分混合,与本文模拟结果接近.
综上,通过对矩形喷动床的最小喷动速度、单颗粒循环时间和混合时间的模拟及与文献结果进行对比可知,本文采用CFD-DEM 耦合模块对颗粒在喷动床中喷动特性的研究是可靠的.
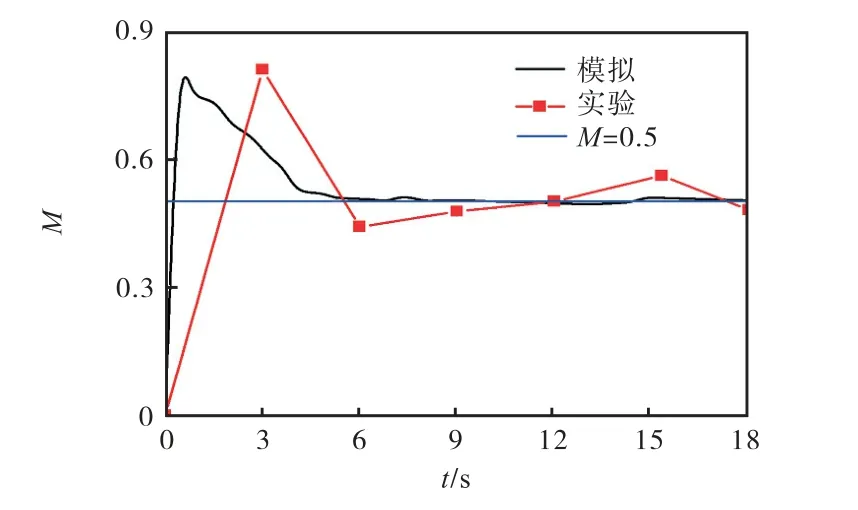
图3 混合指数模拟与文献[17]对比 Fig. 3 Comparison of simulated mixed index and literature
3.2 矩形喷动床与柱锥形喷动床对比
物料的静止床层高度为170 mm,对喷动速度分别为ums、1.1 ums、1.2 ums时的喷动情况进行观察.颗粒的喷动程度随着喷动速度的增加而增加.当us=1.2 ums时,在喷动过程中会出现少量颗粒飞出喷动床的现象.因此,在矩形喷动床与柱锥形喷动床对比研究中,采用的喷动速度为1.1 ums.
3.2.1 喷动床内气体压力
图4 为us=1.1 ums、t=5 s 时,两种喷动床内气体压力的分布情况(XZ 平面,Y=0 mm).两种喷动床的气体压力分布均呈现出中心区域压力较大,越接近壁面气体压力越小,且呈对称分布.
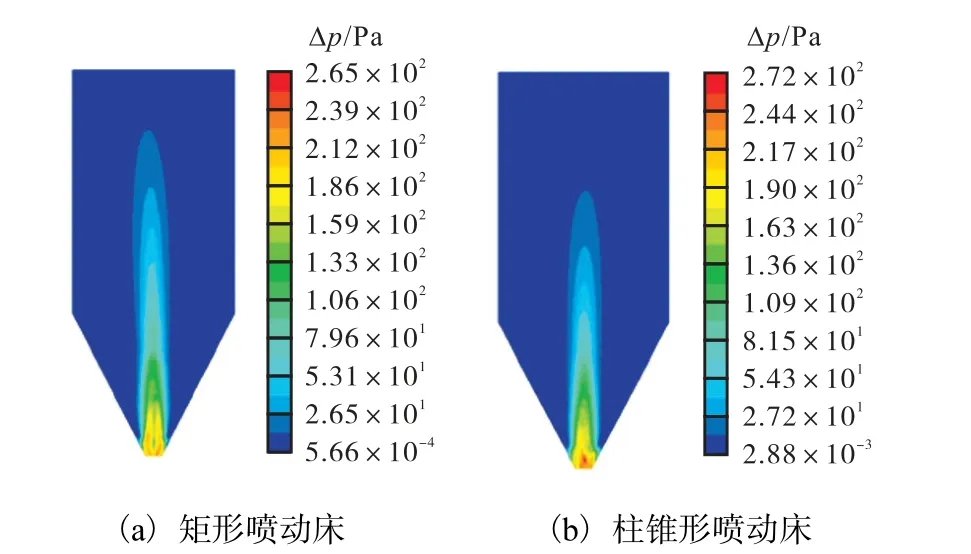
图4 矩形喷动床和柱锥形喷动床气体压力对比 Fig. 4 Gas pressure comparison of rectangular spouted bed and cylindrical cone spouted bed
图5 所示为Z=369 mm(即柱锥交界面)、569 mm和769 mm 时,XZ 平面(Y=0 mm)上的床层压力沿X轴的变化情况.可以看出:随着高度的增加,床层压力递减,柱锥形喷动床的压力值小于矩形喷动床内的压力值.
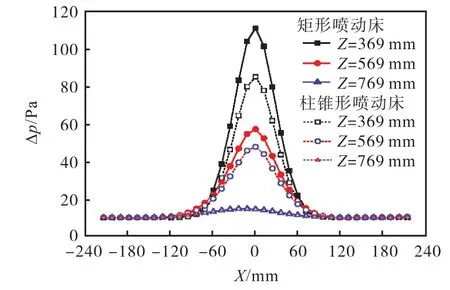
图5 矩形喷动床和柱锥形喷动床在不同平面的床层压力对比(us=1.1 ums) Fig. 5 Pressure comparison of rectangular spouted bed and sylindrical spouted bed at different planes(us=1.1 ums)
3.2.2 混合特性
图6 为Z=120 mm 和Z=369 mm(即柱锥交界面)时,混合指数随时间的变化过程.可以看出:在0~2.8 s,柱锥形喷动床的混合速率略高于矩形喷动床的混合速率,这是因为矩形喷动床内的气体压力较大,气流速度比柱锥形喷动床低,颗粒受气流作用,其加速度要比柱锥形喷动床略低;在2.8 s 以后,矩形喷动床和柱锥形喷动床内颗粒均达到了混合均匀状态,即 M=0.5.一般加热过程远远大于2.8 s,因此,前期的混合特性差异对加热过程影响很小,可以忽略,即矩形喷动床与柱锥形喷动床在颗粒混合特性方面基本一致.
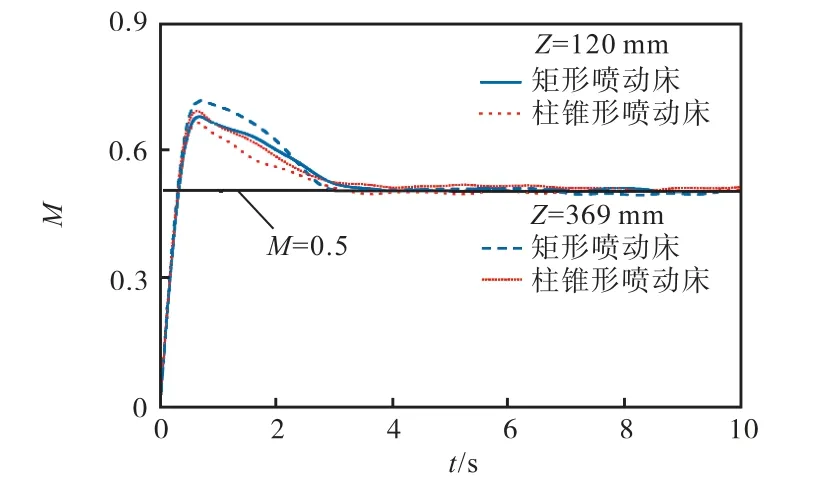
图6 us=1.1 ums 颗粒混合特性对比 Fig. 6 Comparison of particle mixing characteristics at us=1.1 ums
3.2.3 单颗粒循环时间
为了保证颗粒循环时间的准确性,分别在Z=40、80、120、170 mm 的XY 平面内随机选取50 个颗粒,通过分析颗粒在运动过程中高度的变化,每相邻两次位于同一高度时为颗粒运动一个循环,记录其循环时间.通过统计10 s 内颗粒的循环次数和循环时间,计算出单颗粒平均循环时间.
不同高度颗粒的运动过程均呈现出良好的循环特性(图7),而且柱锥形喷动床与矩形喷动床内保持了较好的一致性.
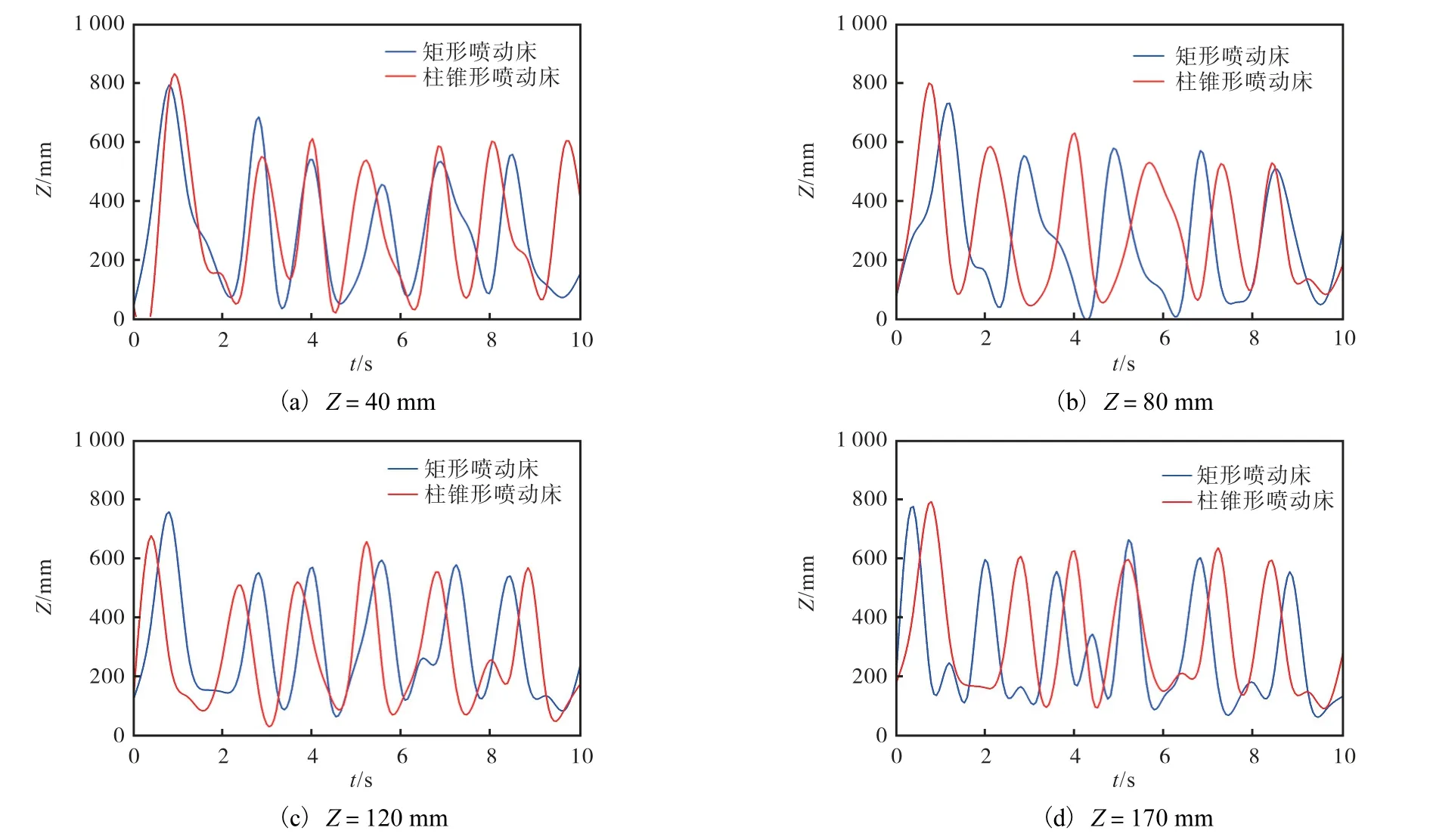
图7 us=1.1 ums 时的矩形喷动床与柱锥形喷动床单颗粒循环时间对比 Fig. 7 Comparison of cycle time between rectangular spouted bed and sylindrical spouted bed at us=1.1 ums
表3 为不同喷动床的不同位置单颗粒循环时间比较.矩形喷动床的单颗粒平均循环时间为1.9 s,柱锥形喷动床的单颗粒平均循环时间为1.7 s,矩形喷动床的内部压力较大导致颗粒运动速度较小,其循环时间略长.但是,矩形喷动床在不同位置的单颗粒循环时间相差较小,说明矩形喷动床内气流速度比柱锥形喷动床更加平稳.

表3 不同位置单颗粒循环时间比较 Tab. 3 Comparison of cycle time of single particle in different positions
3.2.4 颗粒运动情况
图 8 表示进口气速 us=1.1 ums,Z=369、569、769 mm 时,XZ 平面(Y=0 mm)上的颗粒轴向速度沿X 轴的分布规律.由此看出:越接近喷射区的颗粒轴向速度越大,越接近壁面处的颗粒轴向速度越小;随着轴向位置的升高,因颗粒的动能减小使得颗粒的速度呈现下降趋势.矩形喷动床与柱锥形喷动床的颗粒速度场分布基本一致.
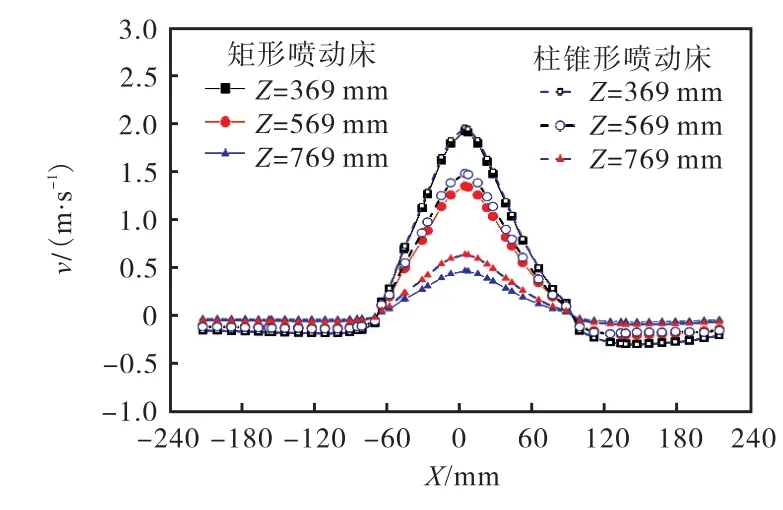
图8 矩形喷动床和柱锥形喷动床中颗粒轴向速度对比(us=1.1 ums) Fig. 8 Axial velocity comparison of particles in different planes of rectangular spouted bed and cylindrical spouted bed(us=1.1 ums)
考虑到矩形喷动床中流场分布受其结构形状的影响,有些位置的流速较小或者颗粒受力处于平衡状态,可能会出现颗粒停滞现象,不能更好地参与到喷动循环中,物料的集聚会影响加热的均匀性.本文在矩形喷动床内选取喷动床底部(Z=10 mm)和中间(Z=80 mm)两个平面中靠近壁面的边缘位置分别随机选取100 颗颗粒,观察其位置变化情况,从而确定边缘颗粒在喷动过程中是否出现停滞情况.如图9 所示,模拟开始时,颗粒受入射气体的影响移动到一个较高的位置,随着稳定喷动过程的形成,颗粒运动范围也逐渐稳定,但与图7 相比,颗粒运动范围明显减小.通过分析矩形喷动床在XY 平面(Z=80 mm)的压力分布,发现在矩形喷动床棱角处气体压力最大,如图10 所示.因此,在矩形喷动床底部(Z=10 mm)和中间(Z=80 mm)的棱角处随机取单颗粒分析其运动情况,如图11 所示,发现在某一个时间段,颗粒的Z 坐标基本不变或变化很小,说明颗粒出现停滞现象.因而,在矩形喷动床的结构设计时要充分考虑棱角处颗粒运动问题.
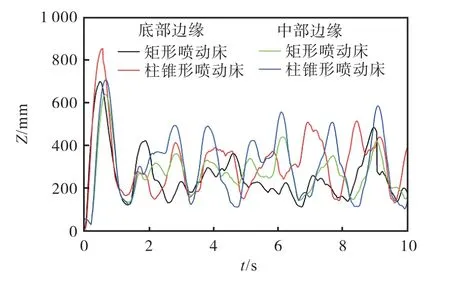
图9 靠近喷动床壁面位置颗粒的位置变化对比 Fig. 9 Comparison of position changes of particles near the pouted bed wall

图10 矩形喷动床内气体压力分布(Z=80 mm) Fig. 10 Distribution of gas pressure in rectangular spouted bed(Z=80 mm)
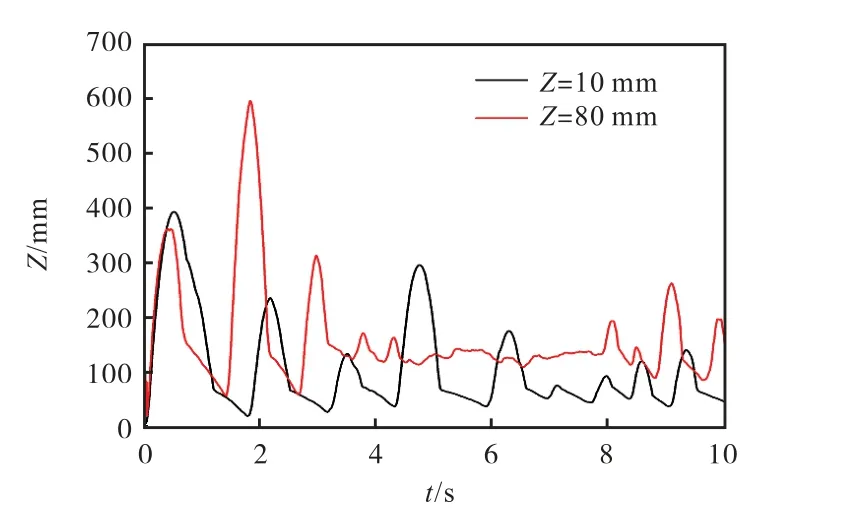
图11 矩形喷动床棱角处颗粒位置随时间的变化 Fig. 11 Change of the position of particles at the edges and corners of rectangular spouted bed with time
4 结 语
本文通过CFD-DEM 法对矩形喷动床与传统柱锥形喷动床中小麦颗粒喷动特性进行对比研究,发现矩形喷动床内的压力较大.针对本文研究的两种喷动床结构和尺寸,颗粒混合均匀时间均为2.8 s.矩形喷动床的单颗粒平均循环时间为1.9 s,柱锥形喷动床的单颗粒平均循环时间为1.7 s,相差较小.两种喷动床的颗粒速度场分布基本一致,颗粒的平均速度差异较小,但通过对靠近喷动床壁面位置颗粒运动研究,发现矩形喷动床在棱角处的颗粒运动随机性较差,主要因为矩形喷动床棱角处气体压力较大.
研究说明,矩形喷动床和柱锥形喷动床的喷动特性基本一致,其结构设计在保证微波场均匀分布的前提下可以利用柱锥形喷动床的设计理论.需要注意的是,对于棱角处颗粒随机运动问题,需要在喷动床中内设结构方面进一步改进.
