对一道概率统计题命制过程的思考

陈万寿 龙宇

[摘   要]概率统计高考试题设计背景新颖，与现实问题的联系紧密，主要考查学生解决实际问题的能力.立足高考数学考查背景，主要分析一道概率统计问题的命制过程，并思考如何命制“好”概率统计题以供学生进行练习.

[关键词]概率统计;二项分布;频率分布直方图

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2019）32-0025-02

统计与概率是高中数学的重要内容.概率统计高考试题强调应用性，以实际问题为背景，构建数学模型，突出考查统计与概率的思想和考生的数据处理能力及应用意识.对此，笔者立足以上考查背景，主要分析广东顺德区的一道考前测试题目的命制意图与命制过程.

一、题目及解答

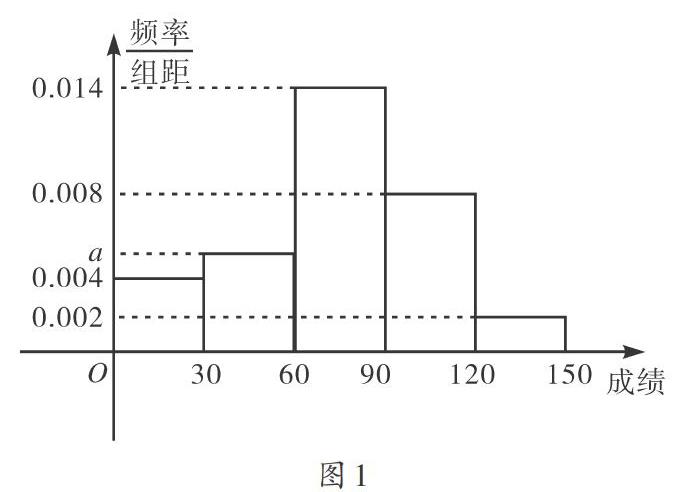
【题目】在高考结束后，省考试院会根据所有考生的成绩划分出一段线和二段线.同学们就可以结合自己的成绩与划线进行决策——填报高考志愿.作为一个学科的评价，也需要有一个标准进行判断.以数学学科为例，在一次考试中，将学生的成绩由高到低排列，将学生的成绩分为一、二、三檔三个层次，前[22%]定为一档，前[58%]到前[22%]定为二档，后[42%]定为三档.在一次全市的模拟考试中，学生数学成绩的频率分布直方图如图1：

（1）根据直方图的信息可知第三档的分数段为[（0，70）]，试估计第二档及第一档的分数段;

（2）在历年的统计中发现，数学成绩为一档的同学其总分过一段线的概率为[0.8]，数学成绩为二档的同学其总分过一段线的概率为[0.5]，数学成绩为三档的同学其总分过一段线的概率为[0.1]，每位同学是否过一段线相互独立.在此次模拟考试中，甲、乙、丙三位同学的数学成绩分别为[65，94，122].请结合第（1）问中的分数段，估计这三位同学总分上一段线的人数的平均值.

二、题目的考查意图与引申

1.题目的考查意图

本题以高考成绩为背景，对所有考生而言，背景公平，且在第（2）问中体现出所有学生即使在数学学科上有差异，但都有机会通过高考划线的一段线，可为正在复习备考的学生提供积极的心理暗示，也增强学生对数学学科应用的认同感.

本题共设计了两个问题，第（1）问考查学生对频率分布直方图的认识以及对统计量“中位数”的认识与理解;第（2）问考查了两个随机变量间的关系，即数学成绩与总分成绩之间的关联，但设问方式则是离散型随机变量的分布以及期望.第（1）问中的分数段是“中位数”的变异，要求学生充分理解“中位数”的定义及算法，并在此基础上进行推广.此问题的难度适中，也具有一定的应用价值，也考查了学生学习迁移的能力.

第（2）问是在第（1）问获得结论的基础上进行的应用判断，考查学生的阅读能力，能够将文本中出现的信息转化为两个随机变量间的关联.本题原本的设计是估计三位同学总分上一段线的人数.后改为目前的问法，让学生在解题的过程中更加有指向性.

2.关于频率分布直方图的编制与思考

数学考试成绩的分数极差为[150]，该按照什么标准进行分组呢？从理论上讲，组距越小，越能反映总体的实际情况.但组距太小，就会造成分组过多，让学生耗费过多的精力在计算上，与目前的高考“多考一点想，少考一点算”相矛盾.如何进行一个折中的选择就是对命题教师的考验.

基于上面的分析，可以选择的组距有：10，15，20，30，50.当组距为[20]时，[150]不能做到均匀分配，与学生常规思维冲突，放弃该组距;组距为[50]，整个成绩仅仅被分为三段，误差太大，也放弃该组距;[15]与[30]视为同一类.为了减小运算量，最终选择组距为[30]进行设计.接下来又出现一个新的问题，如何设计每一段的概率.

为了科学性，使用真实的数据是最合理的.这又涉及运算量的问题，且收集数据较为困难，所以就要进行编制与调整.笔者最终以自己所授课班级学生的考试成绩为依据，进行优化与调整，再折算为频率/组距，必然存在一个坐标为无限小数，为此，笔者在频率分布直方图中设计了一个未知量[a].该设计避免了数据上的问题，也对学生的认知产生了一定的冲击.解题的过程中，要回避[a]的求解，利用频率的基本性质求解.该设计对学生的能力考查又提高了一个层次.

3.关于数学成绩与总分之间关系的设计

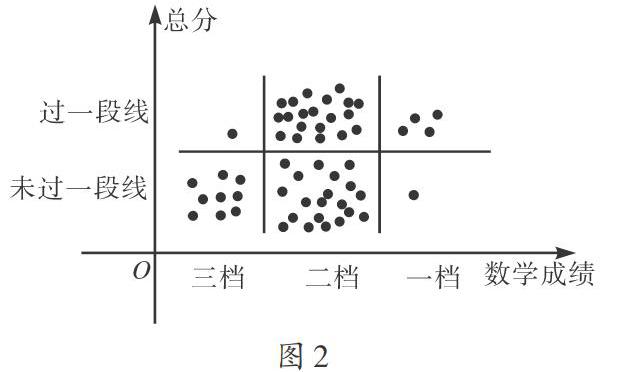
本环节的设计可以考查的知识点很多，比如：数学成绩过一段线的情况与总分过一段线是否相关？我们可以统计相关数据进行分析，并以散点图（如图2）的形式呈现.通过此方式考查学生收集处理数据的能力.

还可考查数学成绩与总分之间的线性回归方程，通过数学成绩预测总分的情况.在本题中，笔者另辟蹊径，设定两个变量相关，并分别给出了三个条件概率，考查学生分析问题、解决问题的能力.本环节的设计还与第（1）问相结合，形成一个整体.该次考试是在高考前的最后一次模拟测试，设计数据的目的是为提高学生的学习信心（数学成绩为三档的同学也有[0.1]的可能过一段线），充分体现了人文关怀.

笔者在第（2）问中设计了甲、乙、丙三位同学进行分析，三位同学分别是三个档次的代表，学生可以通过概率的独立性进行运算.对分布列理解透彻的学生可通过题干信息识别出每一位同学是否过一段线服从二项分布，根据随机变量的可加性，可分别计算三个期望值再求和.因此，笔者在图1的基础上，提出了一个备用问题：你能根据散点图信息，统计学生数学成绩预测所有学生总分过一段线的平均数吗？

（特约编辑 安   平）