基于无人机影像序列的城市精细化三维模型精度评估

陈仁朋　吴熠文　余加勇　何旷宇　薛现凯　李锋

摘   要：为满足数字城市对精细化实景三维模型日益显著的需求，解决传统方法建模效率低的问题，提出一种基于无人机影像序列的城市精细化三维模型构建方法，通过现场25架次的航拍试验，构建了20个300 m×300 m测区范围的精细化模型和1个图书馆建筑精细化模型;利用检查点评估了全部精细化模型的精度，重点讨论了5种航拍高度和4种控制点选取方案对精细化模型精度的影响. 分析结果表明：随着航拍高度降低、控制点数量增加，构建的精细化模型误差减小、精度得到提高;测区范围精细化三维模型最高精度达到平面±3.4 cm、高程±3.1 cm，图书馆单体建筑精细化模型精度达到平面±3.4 cm、高程±1.5 cm;基于无人机序列影像的三维模型构建方法能够满足城市实景模型构建的精度要求，具有重要工程实用价值.

关键词：无人机;倾斜摄影测量;三维模型;精度评估

中图分类号：P237                      文献标志码：A

Method Accuracy Evaluations of Building Urban Detailed 3D Model Based on

the Unmanned Aerial Vehicle Image Sequences and Its Accuracy Evaluatios

CHEN Renpeng1，2，WU Yiwen1，2，YU Jiayong1，2，HE Kuangyu1，2，XUE Xiankai1，2，LI Feng1，2

（1. Key Laboratory of Building Safety and Energy Efficiency of Ministry of Education，Hunan University，Changsha 410082，China;

2. College of Civil Engineering，Hunan University，Changsha 410082，China）

Abstract： In order to satisfy the increasingly significant demand of the digital city for the detailed 3D model and solve the low efficiency problem of traditional modeling method， this paper summarizes a method of building the urban detailed model based on unmanned aerial vehicle （UAV） image sequences. Through the in-situ aerial photography test with 25 sorties， detailed models for 20 experiment area （300 m×300 m） and a library building were built. The accuracy of all detailed models were evaluated by field check points. The effect of 5 different flight heights and 4 different control points on the accuracy of the detailed models were discussed. The results show that the errors of the detailed models can be effectively decreased and the accuracy is improved by declining the flight height or increasing the number of control point. The highest accuracy of detailed models is ±3.4 cm in the plane and ±3.1 cm in the height， respectively. The accuracy of the detailed model for the library building is ±3.4 cm and ±1.5 cm， respectively. The method of building the urban detailed model using UAV image sequences can satisfy the accuracy requirement of the urban real scene model， which has great practical values in practical engineering.

Key words：Unmanned Aerial Vehicle（UAV）;oblique photogrammetry;3D reconstruction;accuracy evaluation

隨着数字城市对城市精细化实景三维模型的需求日益显著，建立真实的三维景观凸显出较高的应用前景和经济价值[1].   数字城市三维模型包括地形和建筑三维模型. 传统航空摄影测量方法不仅影像质量和分辨率相对较差[2]，而且构建的三维建模侧面纹理信息相对缺乏，需要依靠人工从地面拍摄照片来补充纹理信息，对于城市内数以万计的建筑物来说，此方法耗时耗力[3].

无人机（Unmanned Aerial Vehicle，UAV）具有操作容易、数据采集灵活、时效性高、云下飞行等优

点[4-5]，已成为主要的低空遥感平台[6]. 无人机倾斜摄影测量技术是一项新兴的对地观测技术[7]，颠覆了传统航空摄影测量技术，它通过无人飞行平台搭载的多台相机和传感器，从一个垂直和四个倾斜角度获取目标的垂直和倾斜高质量影像，不仅能够获取丰富的地物信息，而且通过定位、融合、建模技术，生成真实的三维城市模型[8].

目前国内外研究者已开展了基于无人机倾斜摄影测量技术的城市三维建模方法研究[9-11]，然而对采用无人机超低空、低空航拍方法来构建城市精细化三维模型的精度影响因素的研究较少[12-14]. 为此，本文提出一种基于无人机影像序列的城市精细化三维模型构建方法，通过大量现场试验评估三维模型的平面和高程精度，重点分析航拍高度和控制点数量对三维模型精度的影响.

1   城市精细化模型构建方法

1.1   无人机影像采集

通过无人机倾斜摄影测量技术，从不同相机位置获取目标区域多个不同角度影像，包括垂直拍摄影像和倾斜拍摄影像.

结合实际情况确定合理的飞行计划，包括飞行高度、线路和速度、影像拍摄角度、相机参数、拍照频率、航向和旁向影像重叠度等参数的设计. 合理的飞行计划能够有效减少外业工作量，并提高后期处理效率和产品精度. 航拍实时记录飞行高度、经纬度、大地高、姿态等信息，用于后续的分析和整理.

1.2   影像畸变差纠正

畸变差主要来源除了相机镜头的机械和光学误差以外，有时也可能源于A/D转换时的电学误差[15]. 畸变差破坏了出入射光线的平行状态，使得像点偏离了理论位置，故不满足三点共线条件. 相机畸变的纠正是径向畸变和切向畸变的总和，即：

式中：xr和yr为径向畸变;xd和yd为切向畸变. 通过标定板利用相机检校软件对相机进行标定，获得畸变参数，对影像进行畸变差纠正.

1.3   影像匀色匀光

在影像获取过程中，受快门速度、曝光度、天气和光照等因素的影响，使得获取的影像出现光照和色彩分布差异较大的现象，继而影响三维模型的制作和应用[16]. 基于Wallis匀光算法原理，选择色彩和光照合适的模板影像，统计其均值和方差参数，借助Wallis滤波器对目标影像灰度的线性分布进行调整. 线性变换式为：

式中：g（x，y）为原始影像在（x，y）处的灰度值;f（x，y）为线性变换后影像在（x，y）处的灰度值;r0、r1分别为线性变换式中的加系数和乘系数[17].

1.4   影像区域网联合平差

影像区域网联合平差技术目的是获得无人机不同拍摄位置和角度采集的影像上每个点的外方位元素. 通过由粗到精的金字塔匹配方法，结合POS信息得到外方位元素，对每级影像同名点进行自动匹配和自由网光束法平差，建立控制点坐标、POS辅助信息、连接点线的影像自检校区域网平差的误差方程，经过联合解算，达到平差结果精度，其线性化误差方程为：

式中：t和X分别表示影像定向未知数和坐标未知数向量;A和B分别表示相应的系数矩阵;l和Pφ分别表示影像坐标观测值向量及其权矩阵[18].

1.5   三维模型表面重建与纹理映射

在确定像机拍摄的外方位元素后，通过空中三角测量和自动图像匹配技术对场景进行数字化重建，并输出密集三维点云. 表面网格重建是曲面重建的重要前處理，根据区域的有限个点集将区域划分为相连的三角面网络，三角面的形状和大小取决于不规则分布的测点的密度和位置，这样能够避免地形平坦时的数据冗余，又能按地形特征点表示数字高程特征.

最后进行三维模型纹理映射，是增强模型视觉效果的关键步骤. 基于无人机倾斜摄影测量技术的纹理映射是多视图纹理映射，即通过多幅来自不同视点的图像作为纹理图，具体实现方法为：数据获取、可见性判断、重新配置纹理分布、融合纹理边界、纹理空洞修补等[19].

1.6   三维模型精度评估

根据CityGML标准对多细节层次（Levels of Detail，LOD）的划分，针对建筑模型点位精度划分为4个级别，如表1所示[20].

对于每个重构的三维精细化模型，均对其平面和高程精度进行评估. 首先采用自动型全站仪高精度地获取所有检查点的实测三维坐标（Xi，Yi，Zi），然后从重构的三维模型中识别相应检查点的影像三维坐标（XOi，YOi，ZOi）， 进行误差统计分析，采用式（4）（5）计算出三维模型在水平和高程方向的均方根误差RMSEXY、RMSEZ：

式中：n为检查点个数. 并利用箱形图对模型构建误差值进行中误差、平均值和离散性进行统计分析. 箱形图包含的数据点如图1所示，当上、下四分位数之差和上、下限值之差越小时，数据的离散性越小.

2   现场试验

2.1   试验区域

航拍试验区域位于长沙市岳麓区中南大学新校区（东经112.939 1°，北纬28.152 8°），以图书馆为中心并向四周延伸而形成300 m×300 m的正方形区域，如图2所示. 试验区域内包含建筑物、道路、桥梁、绿地等城市要素，可较好地模拟城市精细化三维模型构建. 图书馆为试验区域内最高建筑，其长宽高分别为150 m、72 m、32 m.

2.2   试验设备

本次航拍试验采用大疆经纬M210-RTK型号无人机，搭载大疆禅思X5S相机，最大像素2 080万，镜头焦距15 mm，试验设备如图3所示. 无人机前方和下方配备立体视觉系统，上方配备红外感知系统，可实现前方、下方和上方避障. M210-RTK无人机配备有实时动态差分（Real-time Kinematic，RTK）模块，可实时接收全球定位系统（Global Positioning System，GPS）和北斗导航卫星系统（Beidou Satellite System，BDS）信号，利用地面基准站进行载波相位差分改正，可获取平面1 cm、高程2 cm精度的无人机飞行定位信息.

测点（控制点和检查点）采用瑞士Leica TS30型号自动型全站仪测量，其精密测距标称精度为0.6 mm +1 ppm，免棱镜测距的标称精度为2 mm +2 ppm，测角标称精度为±0.5″. 并采用天宝DiNi12电子水准仪复核测点高程，其标称精度为每公里往返观测标准误差为±0.3 mm.

2.3   控制点和检查点选取

控制点和检查点共两组，第1组分布在300 m×300 m试验区域内地面，共25个测点，用于区域内三维模型构建及其精度评估;第2组分布在图书馆建筑外表面，共98个测点，用于单体建筑精细化模型构建及其精度评估.

第1组25个测点均匀分布在300 m×300 m试验区域，并埋设直径1 cm、长度7 cm的不锈钢测量标志. 设计4种不同的三维模型构建方案，根据均匀分布控制的原则，分别选取其中3、6、9、12个测点作为控制点，其余点均为精度检查点，控制点均匀分布在试验区内，如图4所示. 按照一级导线和二等水准测量的技术要求，采用Leica TS30型号自动型全站仪和天宝DiNi11型号电子水准仪精确测量地面测点的平面和高程坐标，其测量精度均优于±3 mm. 控制点标志采用长宽均为1 m的旗帜布制作，旗帜布上印制黑白相间的辐射状图案及编号，图案中心预留直径3 mm的孔洞，便于对准不锈钢标志的中心，如图5所示.

第2组98个测点分布在图书馆建筑外表面上，按照10 m、20 m、30 m 3个不同高度分层布置，如图6所示. 在建筑物4个侧面的10 m和30 m高度处各取2个测点作为控制点，共16个控制点，其余测点作为检查点. 选取图书馆建筑外表面具有较强反射性且具有明显特征的点位作为测点，不需额外粘贴反射标志，直接采用Leica TS30自动型全站仪的免棱镜功能进行三维坐标测量，平面和高程测量精度均优于±5 mm.

2.4   影像采集

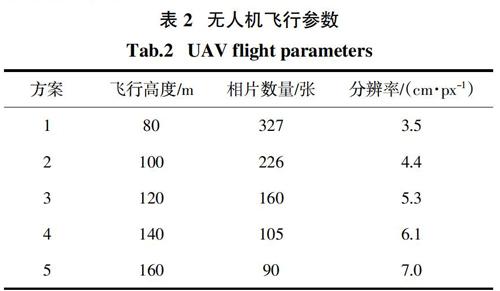
为重构试验区域内地物和地貌的精细化三维模型，并评估三维模型的精度，共设计了5种影像采集方案，每个方案进行1组垂直拍摄和4组倾斜拍摄. 5种方案中无人机飞行高度分别为80 m、100 m、120 m、140 m和160 m，对应的影像分辨率和数量如表2所示. 采用DJI GS Pro软件规划无人机航拍路径及控制无人机飞行，相机倾斜角设置为45°，航向重叠率和旁向重叠率均设置为70%. 共进行了25架次航拍，共采集908张相片.

3   模型构建与精度分析

3.1   模型构建

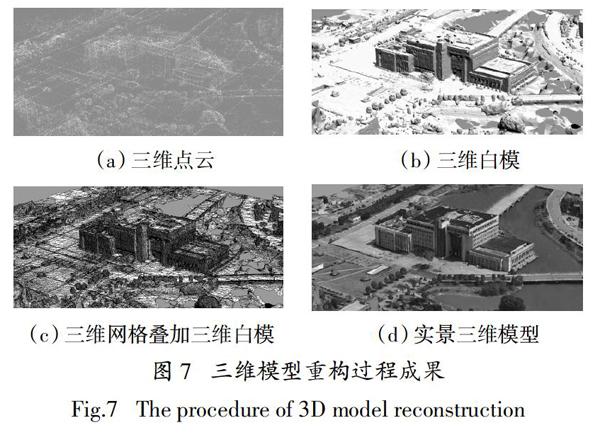
对于300 m×300 m测区三维模型，本次试验设置了5个飞行高度和4种控制点方案，共重构了20个三维模型;对于图书馆单体建筑精细化模型，本次试验利用飞行高度为80 m的影像序列进行精细化三维模型构建，重构了1个三维模型. 首先对影像预处理、影像区域网联合平差、导入控制点及坐标;然后按照空中三角测量生成密集三维点云、生成三维白模、表面网格重建生成三角网、纹理映射生成实景三维模型等步骤构建三维模型，如图7所示.

3.2   测区模型精度分析

对300 m×300 m测区范围的整体三维模型进行精度分析. 不同飞行高度、不同控制点数量下共构建了20个三维模型. 计算出每个模型中所有检查的误差值，即实测三维坐标与模型中识别三维坐标值的差值.

不同飞行高度下，构建的三维模型平面和高程精度如图8所示. 飞行高度为80 m时，不同控制点数量（3、6、9和12个）对应的三维模型平面方向均方根误差分别为5.8 cm、4.9 cm、4.0 cm、3.4 cm，高程方向均方根误差分别为12.1 cm、5.9 cm、5.1 cm、3.1 cm. 飞行高度为160 m时，不同控制点数量对应的三维模型平面方向均方根误差分别为14.9 cm、14.2 cm、12.5 cm、10.6 cm，高程方向均方根误差分别为16.5 cm、10.0 cm、8.1 cm、7.0 cm.

当无人机飞行高度增加时，各控制点方案的三维模型平面和高程误差均逐渐增大，精度逐步降低. 当飞行高度由160 m减小至140 m时，平面均方根误差减小较多，飞行高度对模型精度的水平精度影響较为明显. 当飞行高度为80 m时，平面和高程精度最高. 原则上要求无人机飞行高度不低于建筑物1.5倍高度，在此前提下，当飞行高度越低时，模型的平面和高程精度越高.

在不同控制点数量下构建的三维模型精度如图9所示. 当控制点数量为3时，不同飞行高度（80 m、100 m、120 m、140 m、160 m）对应的平面均方根误差分别为5.8 cm、9.0 cm、10.1 cm、10.9 cm、14.9 cm，高程均方根误差分别12.1 cm、14.4 cm、15.8 cm、16.4 cm、16.5 cm. 当控制点个数为12时，不同飞行高度对应的平面均方根误差分别为3.4 cm、4.8 cm、6.2 cm、6.8 cm、10.6 cm，高程均方根误差分别3.1 cm、5.4 cm、6.7 cm、6.9 cm、7.0 cm. 随着控制点数量的增加，三维模型的平面和高程误差均逐渐减小，精度越来越高. 因此，控制点数量越多时，模型的平面和高程精度越高. 当控制点数量由3个增加至6个时，高程均方根误差明显减小，控制点数量对模型高程精度影响显著.

当飞行高度为80 m、控制点数量为12时，平面均方根误差为3.4 cm，高程均方根误差为3.1 cm，三维模型的平面精度和高程精度达到最高. 所有三维模型的水平及高程精度均满足精细化模型精度要求，故在满足模型精度的情况下可尽量减少控制点数量（但至少为3个）或提高飞行高度.

3.3   测区模型误差离散性分析

对300 m×300 m测区范围的整体三维模型进行两组误差离散性分析，第1组选取控制点数量为12时构建的5种不同飞行高度的三维模型;第2组选取飞行高度为80 m时构建的4种不同控制点方案的三维模型.

在第1组5个三维模型中，控制点数量均为12个，飞行高度由80 m 增加到160 m，误差箱形图如图10所示. 当飞行高度为160 m时，平面误差上限值为16.0 cm，下限值为1.7 cm，上四分位数为13.8 cm，下四分位数为6.9 cm，中位数为10.0 cm，平均数为9.7 cm;高程误差上限值为10.6 cm，下限值为2.2 cm，上四分位数为9.5 cm，下四分位数为2.7 cm，中位数为4.7 cm，平均数为5.9 cm. 随着飞行高度的增加，模型平面和高程误差的上、下四分位数之差和上、下限值逐步增大，离散性逐渐增大，精度降低. 当飞行高度为80 m时，误差离散性最小，精度最高;当飞行高度由120 m降低至100 m时，平面误差和高程误差离散性明显减小;当飞行高度小于120 m时，误差离散性较小;当飞行高度大于120 m时，误差离散性较大.

在第2组4个三维模型中，飞行高度均为80 m，控制点数量由3个增加至12个，误差箱形图如图11所示. 随着选取控制点数量的增加，三维模型误差的上、下四分位数之差和上、下限值逐步减小，离散性逐步减小，精度提高. 当控制点个数为12个时，离散性达到最小，精度最高;当控制点数量由3个增加至6个时，平面误差和高程误差离散性明显减小. 故当控制点数量小于6个时，误差离散性较大;当控制点数量大于6个时，误差离散性较小.

3.4   单体建筑物精细化模型精度分析

选取无人机飞行高度为80 m、建筑物外表面控制点数量为12个的实施方案，重构图书馆建筑精细化三维模型，对其精度进行分析. 建筑物外表面检查点数量共86个，分布在建筑物10 m、20 m、30 m 3个高度层次，如图12所示.如表3所示，三维模型在X轴、Y轴、高程方向的三维模型平面精度基本相同，高程精度随着位置增高而提高，各方向各高度的均方根误差都低于3.4 cm. 最后，计算全部检查点的均方根誤差，其平面和高程标准差分别为±3.4 cm、

±1.5 cm，该精度远高于精细化建筑模型精度要求. 上述精度分析表明，采用无人机超低空、低空飞行航拍方法可以获取高精度的地物和地貌精细化三维模型.

4   结   论

本文提出一种基于无人机影像序列的城市精细化模型构建方法，通过无人机影像采集、影像畸变纠正、影像匀色匀光、影像区域联合平差、三维表面重建和纹理映射等步骤实现模型重构，能完全真实反映城市地形地貌，并通过大量现场无人机航拍试验和内业建模工作，对构建的精细化模型进行了精度分析，得出以下结论：

1）当飞行高度为80 m且控制点数量为12个时，

平面均方根误差为±3.4 cm，高程均方根误差为±3.1 cm，三维模型的平面和高程精度达到最高;当飞行高度小于120 m时，且控制点数量大于6个时，误差离散性较小.

2）通过对单体建筑物精度进行评估，检查点所在的高度越高，高程精度有所提高，平面精度基本一致. 飞行高度为80 m且控制点个数为12个的三维模型的平面均方根误差为±3.4 cm，高程均方根误差为±1.5 cm.

综上所述，基于无人机序列影像的三维模型构建方法可达到厘米级精度，这不仅能够满足城市实景模型构建的精度要求，而且操作容易、数据采集灵活、时效性高，具有重要工程实用价值. 在今后的工作中，将从影像重叠率、拍摄倾斜角度、控制点空间分布、天气状况等精度影响因素进行综合分析.

参考文献

[1]    康志忠. LiDAR数据与数字影像的配准和地物提取研究[D]. 武汉： 武汉大学遥感信息工程学院，2004：5—60.

KANG Z Z. Registration and feature extraction of LiDAR data and digital image[D]. Wuhan：School of Remote Sensing and Information Engineering，Wuhan University，2004：5—60.（In Chinese）

[2]    IMMERZEEL W W，KRAAIJENBRINK P D A，SHEA J M，et al.  High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles[J]. Remote Sens，2014，150：93—103.

[3]    王建强，钟春惺，江丽钧，等. 基于多视航空影像的城市三维建模方法[J]. 测绘科学，2014，39（3）：70—74.

WANG J Q，ZHONG C X，JIANG L J，et al. 3D city modeling construction based on multi-view aerial images[J]. Science of Surveying & Mapping，2014，39（3）：70—74.（In Chinese）

[4]    NEITZE F，KLONOWSK J. Mobile 3D mapping with a low-cost UAV system[J]. Remote Sensing and Spatial Information Sciences，2011，38：1—6.

[5]    罗隆福，李冬，钟杭. 基于改进RRT的无人机电力杆塔巡检路径规划[J]. 湖南大学学报（自然科学版），2018，45（10）：80—86.

LUO L F，LI D，ZHONG H. Path planning of unmanned aircraft inspection for electric towers based on advanced RRT algorithm[J]. Journal of Hunan University（Natural Sciences），2018，45（10）：80—86.（In Chinese）

[6]    李德任. 论“互联网+”天基信息服务[J]. 遥感学报，2016，20（5）：708—715.

LI D R. The “Internet Plus” space-based information services[J]. Journal of Remote Sensing，2016，20（5）：708—715.（In Chinese）

[7]    吴熠文，陈仁朋，余加勇，等. 无人机倾斜摄影测量技术及其工程应用研究进展[J]. 湖南大学学报（自然科学版），2018，45（S1）：167—172.

WU Y W，CHEN R P，YU J Y，et al. Research and development of unmanned aerial vehicle-based oblique photogrammetry and its engineering applications[J]. Journal of Hunan University（Natural Sciences），2018，45（S1）：167—172.（In Chinese）

[8]    谭金石，黄正忠. 基于倾斜摄影测量技术的实景三维建模及精度评估[J]. 现代测绘，2015，38（5）：21—24.

TAN J S，HUANG Z Z. Three dimensional true modeling and precision evaluation base on oblique photogrammetry technology[J]. Modern Surveying & Mapping，2015，38（5）：21—24.（In Chinese）

[9]    AJAYI O G，SALUBI A A，ANGBAS A F，et al. Generation of accurate digital elevation models from uav acquired low percentage overlapping images[J]. International Journal of Remote Sensing，2017，38（8）：3113—3134.

[10]  COVENEY S，ROBERTS K. Lightweight UAV digital elevation models and orthoimagery for environmental applications：data accuracy evaluation and potential for river flood risk modelling[J]. International Journal of Remote Sensing， 2017， 38（8）： 3159—3180.

[11]  張纯斌，杨胜天，赵长森，等. 小型消费级无人机地形数据精度验证[J]. 遥感学报，2018，22（1）：185—195.

ZHAGN C B，YANG S T，ZHAO C S，et al. Topographic data accuracy verification of small consumer UAV[J]. Journal of Remote Sensing，2018，22（1）：185—195.（In Chinese）

[12]  HARWIN S，LUCIEER A，OSBORN J. The impact of the calibration method on the accuracy of point clouds derived using unmanned aerial vehicle multi-view stereopsis[J]. Remote Sensing，2015，7（9）：11933—11953.

[13]  LUCIEER A，TURNER D，KING D H，et al. Using an Unmanned Aerial Vehicle （UAV） to capture microtopography of antarctic moss beds[J]. International Journal of Applied Earth Observation & Geoinformation，2014，27（4）：53—62.

[14]  LUCIEER A，JONG S M D，TURNER D. Mapping landslide displacements using Structure from Motion （SfM） and image correlation of multi-temporal UAV photography[J]. Progress in Physical Geography，2014，38（1）：97—116.

[15]  徐秋辉. 无控制点的无人机遥感影像几何校正与拼接方法研究[D]. 南京：南京大学地理与海洋科学学院，2013：12—56.

XU Q H. A method of geometric correction and mosaic of unmanned aerial vehicle remote sensing image without ground control points[D]. Nanjing：School of Geography and Ocean Science，Nanjing University，2013：12—56.（In Chinese）

[16]  夏孟涵. 航空影像无控拼接及匀光匀色方法研究[D]. 武汉：武汉大学遥感信息工程学院，2017：24—68.

XIA M H. Research on pose-free stitching and color consistency correction for aerial images[D]. Wuhan：School of Remote Sensing and Information Engineering，Wuhan University，2017：24—68.（In Chinese）

[17]  王博，张永军，陈奇. 一种改进的自适应Wallis滤波算法[J]. 测绘科学，2015，40（5）：95—98.

WANG B，ZHANG Y J，CHEN Q. An improved adaptive algorithm of Wallis filter[J]. Science of Surveying and Mapping，2015，40（5）：95—98.（In Chinese）

[18]  李德仁，鄭肇葆. 解析摄影测量学[M]. 北京：测绘出版社，1992：109—120.

LI D R，ZHENG Z B. Analytical photogrammetry[M]. Beijing：Surveying and Mapping Publishing House，1992：109—120.（In Chinese）

[19]  万刚. 无人机测绘技术及应用[M]. 北京：测绘出版社，2015：206—209.

WAN G. Unmanned aerial vechicle surveying and mapping technology and application[M]. Beijing：Surveying and Mapping Publishing House，2015：206—209.（In Chinese）

[20]  高山，陈思. 城市三维建模技术与标准研究[J]. 测绘通报，2013（3）：95—97.

GAO S，CHEN S. Research on technique and standard of 3D city modeling[J] .Bulletin of Surveying and Mapping，2013（3）：95—97.（In Chinese）