近爆冲击波和破片复合作用下混凝土空心砌块墙防护技术研究

田力　王若晨

摘   要：为探究在不同冲击波和破片复合荷载作用下混凝土空心砌块填充墙的损伤特征和防护技术，通过ANSYS/LS-DYNA软件建立了混凝土空心砌块填充墙各部件、破片和炸药的模型，得到了比例距离、破片尺寸、起爆点对墙体的位移响应的影响以及在聚脲弹性体与钢丝网共同加固条件下墙体所能承受的极限炸药质量和较为经济的防护厚度. 结果表明：通过与试验对比验证，本文的研究方法是可靠的;在近爆冲击波和破片复合作用的条件下，比例距离不能作为判定墙体受损严重程度的依据;同等质量下，减小破片尺寸使墙体破坏加重;改变起爆点对墙体破坏程度的影响微弱;在增加防护后，墙体抗爆性能明显加强，采用5 mm聚脲弹性体和钢丝网加固的墙体在炸药距离1.2 m时的能够抵抗的等效TNT炸药质量在8.296 kg和11.376 kg之间;当炸药距离为1.2 m，等效TNT炸药质量为2.456 8 kg时，较为经济的防护手段是聚脲弹性体厚度和钢丝网钢丝直径均为3 mm. 本文成果可为混凝土空心砌块填充墙抗爆性能及其防爆技术的研究提供重要参考.

关键词：冲击波;破片;混凝土空心砌块墙;数值分析;变形;防护

中图分类號：TU318                     文献标识码：A

Study on Protection Technology of Concrete Hollow Block Wall Subjected

to Combined Effects of Close Blast Shock Waves and Fragments

TIAN Li1，2，WANG Ruochen1

（1. School of Civil Engineering，Tianjin University，Tianjin 300350，China;

2. Key Laboratory of Coast Civil Structure Safty of Ministry of Education，Tianjin University，Tianjin 300350，China ）

Abstract： In order to explore the failure rule and protection technology of masonry walls under the combined effects of blast and fragment loading， the finite element program ANSYS/LS-DYNA was used to establish the model of masonry walls， fragments and explosives. The effects of the scaled distance， fragments size and initiation points on the displacement response of masonry walls were obtained. Both the ultimate load produced by explosive that the masonry walls can resist and the economical protective method of masonry walls under the protection of polyurea elastomer and steel mesh were obtained. The results show that the research method was reliable according to the comparison between the test results and simulation results. The scaled distance cannot be used to judge the damage severity of masonry walls under the blast and fragments loading. Decreasing the size of fragments can increase the damage of masonry walls in the same condition of fragments quality. The effect of different initiation points on the damage level of masonry walls was weak. The protection of polyurea elastomer and steel mesh can improve the blast resistance of masonry walls. When the distance from explosion was 1.2 m， the masonry wall protected by 5 mm polyurea elastomer and steel mesh can carry the load produced by the quality of equivalent TNT explosive between 8.296 kg and 11.376 kg. When the distance from explosion was 1.2 m and the equivalent TNT explosive quality was 2.4568 kg， 3 mm polyurea elastomer and steel mesh were the economical protective measure. The results can provide references for masonry walls anti-explosion theory and protection technology.

Key words： shock waves;fragment;concrete hollow block wall;numerical analysis;deformation;protection

混凝土空心砌块在我国应用广泛，它作为墙体砌筑材料不仅可以充分利用我国各种丰富的天然轻集料资源和一些工业废渣来降低生产成本，而且同时可以减少环境污染等社会问题. 但因为混凝土空心砌块填充墙（以下简称为砌块填充墙）强度较低，周围约束弱所以在爆炸作用下极易发生破坏. 一旦有一定当量的爆炸物爆炸，可能材料强度较高的受力构件没有倒塌，而较为脆弱的砌块墙会损毁或崩溃. 因此砌块填充墙在不同冲击波和破片复合荷载作用下的损伤和防护研究具有重要意义.

国内外学者开展了很多关于爆炸冲击波对填充墙破坏作用以及对冲击波和破片复合荷载的研究：Zhan等[1]通过对16个未加筋黏土砖墙的爆炸试验，研究了在瓦斯爆炸下不同的边界条件、砌筑方式和砖墙厚度等参数对墙体的影响，记录并分析了瓦斯爆炸的压力时间历程、壁面位移时程和壁面破坏模式;Badr等[2]对6个全尺寸混凝土砌块墙在自由場爆炸荷载下进行了试验，将槽钢用冷弯型钢钉固定在墙背上，并与不加固的普通墙壁进行比较，发现可以显著提高墙体平面抗爆能力;郭玉荣等[3]利用AUTODYN研究了12墙，24墙和加固24墙，得到砌体墙在近爆冲击波荷载作用下砌体墙的荷载分布规律及碎块抛射速度规律;王军国[4]研究了不同聚脲弹性体厚度、粘贴位置和本构参数对砖砌体墙在爆炸荷载下动态响应的影响规律;段新峰等[5]利用LSDYNA软件模拟了冲击波与破片复合载荷，分析冲击波单独作用及冲击波与破片联合作用下I型夹层板失效模式和吸能特性. 但是目前对冲击波和破片复合作用下的砌块填充墙的研究很少. 因为使用预制破片以加强爆炸威力的例子在现实中比较普遍，所以破片对建筑的侵彻作用不可忽视.

本文计算分析的基本假定：炸药爆炸、冲击波和破片作用于砌块墙的全过程满足能量守恒条件、动量守恒条件和质量守恒条件. 在计算过程中，要满足材料的本构关系、结构的边界条件、初始条件和约束条件.

本文基于有限元软件ANSYS/LS-DYNA建立砌块墙、炸药、破片和防护构件的计算模型，分析了比例距离、破片尺寸和起爆点等对砌块填充墙损伤效应的影响规律，研究了在防护条件下的墙体极限抗爆能力和较为经济的防护手段，可为砌块墙抗爆防爆研究提供重要技术参考.

1   计算模型和材料参数

1.1   计算模型

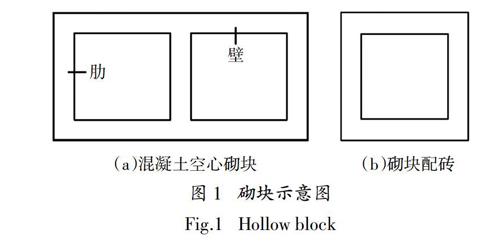
砌块填充墙计算模型采用砌块和砂浆分离式建模. 墙体模型长2 590 mm，厚190 mm，高3 390 mm. 这是因为考虑到现实中建筑底层高度大致为3 600 mm，本文模型高度加上顶砖斜砌和梁高，与实际中建筑底层高度大致相当. 对于模型宽度而言，现有总单元数大致在200万，考虑到电脑配置和计算成本，所以选取2 590 mm作为其长度. 本文模型所选取的尺寸与实际中的砌块墙各部分的尺寸相当，该模型可以代表实际中的混凝土空心砌块填充墙，具有实际的工程应用价值. 普通混凝土砌块和混凝土砌块配砖的尺寸分别为390 mm×190 mm×190 mm和190 mm×190 mm×190 mm[6]，砂浆层厚度取10 mm[7]. 空心砌块示意图见图1，其中砌块壁厚30 mm[6]，肋厚32 mm[6].本文简化了砌块的拐角处的圆弧和砌块的肋上下的差距，不考虑圆弧[8].如果按照实际形状建模，会在局部产生极小的网格，那么计算过程中时间步长会急剧减小，使得在LS-DYNA程序的计算时间延长几倍. 模型各组成部件示意图见图2，其中无防护的砌块填充墙计算模型包含砌块、砂浆、拉结筋、钢筋网片、框架柱和灌芯砌块，有防护的砌块墙还包含双侧角钢、聚脲弹性体和钢丝网. 墙体模型示意图和坐标轴示意图见图3.

依据砌体填充墙结构构造[9]，墙体两侧以拉结筋同框架柱相连，上部由一皮混凝土砖斜砌，下部的空心砌块以灌芯混凝土灌实. 砌块填充墙根部做法[9]如图4所示. 模型底部的灌芯混凝土与室内外地面交界处设为固定端. 由于砌块填充墙上部约束比较弱，所以将其处理为自由端[10]并在上部施加相同重量的荷载.

炸药采用方形ANFO炸药，炸药中心距刚性地面1 400 mm，距填充墙墙体表面1 200 mm. 炸药在中心点爆炸. 炸药爆炸后，产生的冲击波加速破片以产生冲击波和破片的复合荷载. 设置刚性地面以模拟破片飞散时遇到地面发生的反射现象，刚性地面示意图如图3所示. 正方体破片边长为12.5 mm. 空气域长3 540 mm，宽1 825 mm，高3 600 mm，同时对空气设定无反射透射边界.

网格划分后，炸药和空气域单元数约为84万，砌体墙单元数约为87万，破片总数为144个. 计算时间至18 ms结束，取A-A线（见图3）每个砌块的首尾点和B-B线（见图3）每个砌块的中心点作为测点，测量每个测点在18 ms时的位移.

1.2   单元类型和算法

空气、砂浆、炸药、破片、砌块、框架柱模型采用SOLID164单元;因为角钢和聚脲弹性体较薄，所以采用SHELL181壳单元;钢筋网片和拉结筋模型采用BEAM161梁单元. 对炸药和空气采用ALE算法.

1.3   本构模型、参数和接触

本文各部件的本构模型见表1.

炸药模型的状态方程为：

（1）

式中：A、B为材料常数;R1、R2、ω为试验拟合参数;E0为单位体积的初始内能;V为相对体积. 炸药的参数[13]见表2.

空气模型的状态方程为：

式中：C1、C2、C3、C4、C5、C6均为常数;E0 为单位体积的初始内能;V为相对体积. 空气参数见表3.

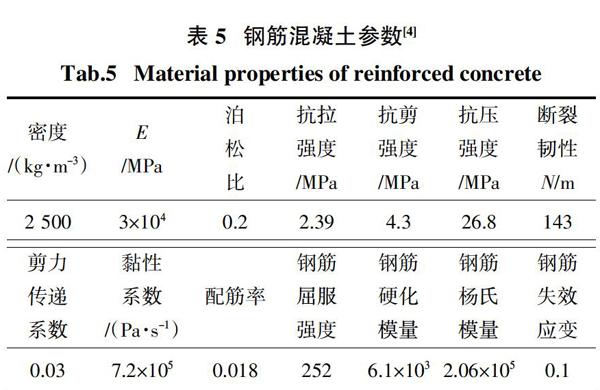
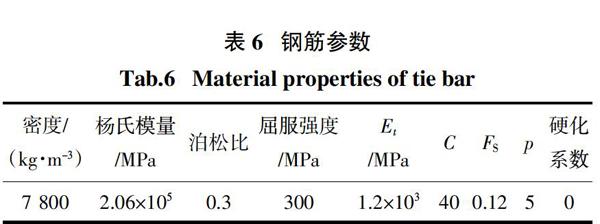
应变率对砌块强度、砂浆强度的影响通过相应的提高系数来考虑. 混凝土空心砌块参数[14]、砂浆参数[1]、灌芯砌块参数[15]见表4;钢筋混凝土柱拟合参数[4]见表5;钢筋的参数见表6.

聚脲弹性体所使用的本构是可以输入不同应变率下的应力-应变曲线的多线段弹塑性材料模型. 聚脲弹性体参数[4]参见表7. 输入的应力-应变曲线[4]参见图5.

模型中混凝土砌块和砂浆层的接触使用固连断开接触. 其中黏接力破坏失效的条件是：

式中：NFLF是法向失效应力;SFLF是切向失效应力，这2个数值由砂浆强度和混凝土强度这2个数值中的较小值确定. 并根据工程经验取抗剪强度的2/3作为接触面的允许抗剪强度[8];接触面允许抗拉强度取允许抗剪强度的0.8倍[8].  本文工况与文献[8]中工况的差异主要在于是否存在高速破片，但是高速破片对砌块墙主要是侵彻穿孔作用，对于砌块墙内部部件砌块与砂浆的相互作用影响微弱，故本文仍采用文献[8]的取值方法. 当黏接力失效后，该接触转化为普通面面接触，此时约束砂浆层和砌块之间的力为摩擦力，摩擦系数取0.7[16].

2   有限元计算方法和本构模型可靠性验证

2.1   砌块墙在冲击波下的动态响应验证

本节通过同W1SS工况试验结果[2]和有限元计算所得的结果的对比以验证本文所使用计算方法的可靠性.

试验所用砌块墙长990 mm，厚190 mm，高2 190 mm. 砂浆层厚10 mm. 炸药是质量为50 kg 的ANFO炸药，距离墙体15 000 mm. 试验使用一个槽钢和两个角钢通过螺栓与墙连接，达到加强墙体的目的. 槽钢和角钢的组合见图6（a），墙体正面示意图见图6（b），约束示意图见图6（c）（d）. 墙体顶部上方无约束，顶部侧边和底部侧边用木块顶紧.

试验中砂浆抗压强度为17.9 MPa;砌块抗压强度为25.85 MPa，弹性模量为2.29×104 MPa;槽钢和角钢的屈服強度为361.4 MPa. 采用LS-DYNA软件建立的模型见图7.

F点（见图7（b））位移时程曲线对比见图8. 从图8可以看出：在冲击波作用下的前25 ms，F点正向最大位移的模拟值为15.9 mm，与试验值相差6%，同时位移达到最大值的时间也十分吻合，模拟较为准确. 试验中砌体墙可视为单向墙，加固后在受到爆炸波冲击时做自由震动. 而从有限元模拟上看，仿真模型也产生了自由振动的现象. 本文选取的本构模型和耦合方式与实际情况存在微小的差异，在可靠性验证试验中，这种差异随时间的增加在LS-DYNA程序计算中会逐渐积累，所以在模拟的后期差异会逐渐增大，这一点不可避免. 但是在模拟的前期，由于误差积累较小可以忽略，由此可说明在25 ms之前的数值模拟是稳定可靠的.

所以从以上分析来看，本文所使用的有限元计算方法和本构模型选取是可靠的.

2.2   冲击波驱动破片验证

本节通过与破片受冲击波驱动的试验和数值模拟的对比来验证本文炸药和破片耦合方式的合理性.文献[13]的试验采用长径比为2、直径为126 mm的圆柱形炸药，预制破片在炸药周向呈圆环状排列一周. 试验中炸药和破片参数见表8. 试验中破片的速度2 082 m/s. 文献[17]中模拟结果为2 027 m/s. 文献[17]和本文数值模拟结果的对比见图9. 本文模拟破片速度是2 100 m/s，与试验值2 082 m/s相差0.56%，模拟较为准确，且图9的两条曲线十分相似. 这说明本文在有限元程序中利用冲击波驱动预制破片的方法和采用炸药破片的耦合方式是有效的.

3   不同冲击波与破片复合作用下砌块墙损

伤效应的参数化分析

3.1   比例距离

比例距离的计算公式见式（4）：

式中：R代表起爆点到炸药所作用的结构之间的距离;W代表等效 TNT 炸药质量. ANFO炸药和TNT炸药的质量换算比为0.8[18].

本节对比分析在不同距离不同炸药量但是在相同比例距离的情况下、由距离引起的比例距离变化的情况下和由炸药量引起的比例距离变化的情况下所引起的荷载因素变化对未防护砌块填充墙损伤效应的影响. 比例距离荷载工况变化见表9.

由图10可看出，当比例距离不变，炸药距离从1 600 mm到800 mm递减时，填充墙的位移在逐渐变小. G1工况下A-A线上最大峰值位移比G5工况下A-A线上最大峰值位移减小了41.23%;G1工况下B-B线上最大峰值位移比G5工况下B-B线上最大峰值位移减小了54.12%（注：A-A线或B-B线上峰值位移最大的那个点在参数变化前后可能并不是同一个点. 以下情况皆同）. 由图11和图12可以看出，当不同炸药量和距离引起比例距离递增时，均使填充墙的位移减小：相同炸药质量下，当炸药距离墙体的距离从800 mm增大到1 600 mm时，G9工况下A-A线上最大峰值位移比G6工况下A-A线上最大峰值位移减小了26.14%;G9工况下B-B线上最大峰值位移比G6工况下B-B线上最大峰值位移减小了15.46%. 在相同距离下，当等效TNT炸药质量从8.296 kg减小到1.037 kg时，G10工况下A-A线上最大峰值位移比G13工况下A-A线上最大峰值位移减小了61.24%;G10工况下B-B线上最大峰值位移比G13工况下B-B线上最大峰值位移减小了43.28%. 在比例距离变化相同时，填充墙位移减小的幅度不同. 图13中，从C点（见图3）位移曲线的变化趋势，即由距离改变的比例距离和由炸药质量改变的比例距离上看，由炸药质量改变的比例距离所表示的荷载变化引起的位移变化更为激烈.

雖然在相同比例距离下，但是同一点却显示出迥异的位移变化，这是由于炸药距离墙体较近造成的. 在远爆条件下，冲击波给与墙体的是近似于某一个时间点下的均布荷载. 但是在近爆条件下，由于炸药的位置距离墙体的每个点均不相同，故当炸药爆炸后，荷载到达墙体各点的时间点和大小均不相同，故仅仅由比例距离来判定在近爆下的爆炸对填充墙的破坏程度是不准确的.

3.2   破片大小

本小节在保证未防护砌块填充墙不变、炸药大小和位置不变、不改变破片总体质量的条件下研究破片尺寸大小对墙体位移相应的影响. 破片尺寸工况见表10.

从图14中可以看出，当破片尺寸从10 mm到18.75 mm递增时，填充墙的位移在不断减小，H4工况下A-A线上最大峰值位移比H1工况下A-A线上最大峰值位移减小了10.53%，H4工况下B-B线上最大峰值位移比H1工况下B-B线上最大峰值位移减小了14.54%. 但是破片尺寸在15 mm和18.75 mm时，峰值位移差异不大，这说明了在冲击波和破片复合作用下，当破片质量不变时，破片的尺寸越大，对墙体造成的破坏越小，但是会趋向一定值.

在同等质量下，破片尺寸对墙体破坏的程度是由破片个数和总体能量同时决定的. 砌块填充墙的薄弱环节在砂浆与砌块的交界处，如果破片尺寸变小，破片总体个数增多，那么破片打到砂浆和砌块的交界处的个数增多，造成的破坏变大. 当破片的尺寸变大时，破片的个数减小，其发散的角度变小，比如当取破片个数为1的极限情况时，破片的位移路径与起爆点和结构最近点的连线的角度为0，破片打到墙体的概率是100%;那么当破片个数增多，部分破片由于发散角增大而打不到墙上，出现能量的损失. 所以在同等质量的条件下，随破片的尺寸减小，相应破片打到砌块填充墙薄弱环节的个数增多，但是能量的损失也会增大，复合荷载对墙体造成的破坏是这两个因素平衡的结果.

3.3   起爆点

本节分析了在相同未防护砌块填充墙、炸药和破片的条件下，改变炸药起爆点的位置对未防护砌块填充墙破坏的影响. 炸药起爆点位置示意图见图15，ANFO炸药质量为5.307 kg，起爆方式和工况见表11.

由图16可知，在起爆点紧贴破片的情况下，对应的墙体位移在所有工况中处于较大值. 这是由于在炸药爆炸时，处于爆心的压强最大，破片处于爆心处可以获得更大的速度，但是相对冲击波的能量减小，所以墙体的位移的最终结果是在这两个因素平衡下得到的.

破片填充墙A-A和B-B处的位移曲线在工况I2到I6时没有显示出规律性. 起爆点处于炸药内部时，其选取对于填充墙在冲击波和破片群复合作用下的损伤影响较小. 在近爆条件下，改变起爆点在炸药内部的位置对于冲击波和破片的耦合方式影响微弱，这种改变不足以对墙体的损伤产生较大影响.

4   防护加固

墙体损伤云图见图17. 从图17可以看出，未防护砌块填充墙在破片和冲击波复合作用下，墙体两侧出现剪切破坏，而中间的砌块由砂浆层的破坏而出现飞散的情况. 砂浆层因厚度较小，强度较弱故而破坏严重. 当砂浆层横向一层完全破坏时，那么该层砌块、拉结钢筋和钢筋网片失去约束，整个脱出墙体. 拉结钢筋只有被破片打到的位置出现少许破坏，整体上在端部两侧有较大的剪切变形.

这说明了墙体两侧的约束薄弱，需要加强两侧的约束，且还需要加强墙体整体吸收能量的能力，降低因墙体局部吸收能量过多而局部砌块飞散破坏的概率.

本文采用了钢丝网与喷涂聚脲弹性体联合加固砌块填充墙的防爆技术手段. 聚脲弹性体是一种喷涂于结构表面以应对动态荷载下结构的破裂、碎片飞溅、变形响应的弹性体聚合物，具有高弹性、低弹性模量和黏弹性的力学性能[4].其中钢丝网和聚脲弹性体均双面布置. 在框架柱与墙体相连处设计两个角钢，角钢的一侧与柱子使用多个膨胀螺丝固结，另一侧紧贴墙体，以加强砌块填充墙两侧的约束，并将钢丝网两侧与固定在柱子上的角钢焊接以加强整体约束. 钢丝网相当于一个“骨架”，那么墙体中心有较大挠度的时候，钢丝网会产生一个反力使得墙体出现“反弹”的现象.

4.1   炸药量

本节分析在只改变炸药质量的情况下，有防护的砌块填充墙在冲击波和破片复合作用下的位移响应. 计算模型中钢丝网直径和聚脲弹性体厚度均为5 mm，炸药起爆点距离结构1.2 m. 炸药量工况见表12

从图18可以看出：在ANFO炸药质量为4.877 kg、7.28 kg、10.37 kg、14.22 kg的条件下，D点（见图3）位移先增大后减小. 当ANFO炸药质量为24.57 kg时，D点位移一直增大. 炸药量逐渐增大时，该点的位移增长速度变大，当10 ms时，D点位移从16.7 mm增大到40.6 mm. 墙体损伤云图见图19. 当位移有返回值且破坏较小时，认为墙体能够抵御该条件下的爆炸荷载，虽然炸药质量为14.22 kg时，D点位移仍具有返回值，但从图19（d）墙体损伤云图上，爆炸对于墙体的破坏严重，产生了较大的空洞，故在该种防护条件下，在距离1 200 mm时，其极限抗爆的ANFO炸药质量是在10.37 kg到14.22 kg之间，对应的等效TNT质量在8.296 kg和11.376 kg之间.

4.2   聚脲弹性体和钢丝网钢丝厚度

本节分析了在改变聚脲弹性体和钢丝网厚度的情况下，有防护的砌块墙在冲击波和破片复合作用下的位移响应. 防护层厚度工况见表13.

不同聚脲弹性体和钢丝网厚度下填充墙迎爆面E点（E点位置见图3）位移时程曲线图见图20. 从图20可以看出，当防护层厚度为3 mm、4 mm和5 mm时，可以到达使墙体回弹的防护效果;当防护层厚度为1 mm和2 mm时，防护层破坏不能使墙体回弹，此时E点位移没有出现返回值. 随着防护层的加厚，防护的效果越来越好，厚度为3 mm和厚度为4 mm的差异不大，但是当厚度为5 mm时的防护效果明显加强. 在距离为1 200 mm时，在等效TNT炸药质量为2.456 8 kg爆炸产生的冲击波和破片复合作用下，墙体防护层的经济厚度是3 mm.

12G614—1   Structure structure of masonry filling wall[S]. Beijing：China Planning Publishing House，2012：11—28. （In Chinese）

[10]  吴加珂. 框-墙连接和砌块嵌固对填充墙平面外性能影响[D].哈尔滨：哈尔滨工业大学土木工程学院，2013：29—31.

WU J K. The influence of connection and block build on masonry-infilled walls in the direction of out-of-plane[D]. Harbin：College of Civil Engineering，Harbin Institute of Technolog，2013：29—31. （In Chinese）

[11]  徐强，曹阳，陈健云，等. 混凝土重力坝接触爆炸的响应及破坏特性分析[J].湖南大学学报（自然科学版），2016，43（7）：62—74.

XU Q，CAO Y，CHEN J Y，et al. Study on the response and damage characteristic of concrete gravity dam subjected to contact explosion[J]. Journal of Hunan University（Natural Sciences），2016，43（7）：62—74. （In Chinese）

[12]  何庆峰，周超. 爆炸移除钢筋混凝土框架柱抗倒塌性能数值模拟[J]. 湖南大学学报（自然科学版），2016，43（11）：61—67.

HE Q F，ZHOU C. Numerical simulation on collapse behavior of rc frames with a column removal under blast loads[J]. Journal of Hunan University（Natural Sciences），2016，43（11）：61—67.（In Chinese）

[13]  SANCHIDRIAN J A. Determination of the JWL constants for anfo and emulsion explosives from cylinder test data[J]. Central European Journal of Energetic Materials，2015，12（2）：177—194.

[14]  吕卫东.爆炸荷载作用下混凝土砌块墙力学性能研究[D]. 西安：长安大学建筑工程学院，2011：24—28.

L？譈 W D. Study on the mechanical properties of concrete masonty wall under blast loading[D]. Xi′an：School of Civil Engineering，Chang′an University，2011：24—28. （In Chinese）

[15]  谢超. 混凝土砌块墙体的爆炸效应分析[D]. 长安大學建筑工程学院，2012：34—38.

XIE C. Blasting response analysis of reinforced concrete masonry walls[D]. Xi′an：School of Civil Engineering，Chang′an University，2012：34—38. （In Chinese）

[16]  韩永利. 基于LSDYNA的墙体抗燃气爆炸能力数值分析[J]. 防震减灾学报，2012，30（3）：298—302.

HAN Y L. Numerical analysis of wall resistance to gas explosion based on LSDYNA[J]. Journal of Disaster Prevention and Mitigation Engineering，2012，30（3）：298—302. （In Chinese）

[17]  印立魁，蒋建伟.立方体预制破片战斗部破片初速计算模型 [J].兵工学报，2014，35（12）：1967—1970.

YIN L K，JIANG W J. An initial velocity model of explosively-driven cubical fragments[J]. Acta Armamentarii，2014，35（12）：1967—1970. （In Chinese）

[18]  DAVID B C，CARL S.Young probabilistic estimates of vulnerability to explosive overpressures and impulses[J]. Journal of Physical Security，2010，4（2）：10—29.