离散元法中的集料三维数字模型构建

李智　王子硕　吴文亮　孙杨勇

摘   要：基于三维建模及PFC 5.0平台Fish语言开发一种集料三维离散元模型构建方法. 基于三维建模构建集料颗粒几何形态特征，将集料几何形态导入PFC 5.0平台构建可表征集料几何形态的clump模板;调用clump模板在一定空间内生成clump用于集料离散元模拟. 为评价该方法的有效性及准确性，使用填充度评价clump表征集料几何形态的效果，并采用单元球体数量量化虚拟集料对计算效率的影响，分析几何形态精度与填充算法效率的关系以及填充算法参数对填充度以及单元球体数量的影响. 研究结果表明：集料几何形态特征点数量为1 000 ～ 2 000能够发挥填充算法的优势;按照填充算法推荐参数生成的clump块体可以较好地平衡填充精度与计算效率. 该方法可以实现低成本、高效率生成集料三维离散元模型，为进一步数字化试件仿真提供有力技术支撑.

关键词：道路工程;集料;离散元法;Fish语言

中图分类号：U414                          文献标志码：A

Construction of 3D Digital Model of Aggregate in Discrete Element Method

LI Zhi1，WANG Zishuo1，WU Wenliang1，SUN Yangyong2

（1. School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510641，China;

2. Guangdong Provincial Academy of Building Research Group，Guangzhou 510500，China）

Abstract：Based on 3D modeling and PFC 5.0 platform FISH language，a method for constructing aggregate 3D discrete element model was developed. The aggregate particle geometry was constructed based on three-dimensional modeling and the aggregate geometry was imported into the PFC 5.0 platform to construct a clump template that can characterize the aggregate geometry. Then，clump template was called to generate clump in a certain space for aggregate discrete element simulation. In order to evaluate the effectiveness and accuracy of the method，the degree of filling was used to evaluate the effect of clump on the geometry of the aggregate and the number of unit spheres was used to quantify the impact of virtual aggregates on computational efficiency. The relationship between geometric shape accuracy and the efficiency of the filling algorithm was analyzed. In addition，the effect of fill algorithm parameters on fill level and number of unit spheres was explored. The results show that the number of geometrical feature points of aggregates is 1 000 ～ 2 000，which can take advantage of the filling algorithm. The clump block generated by the recommended parameters of the filling algorithm can better balance the filling precision and calculation efficiency. The method can realize the low-cost and high-efficiency generating three-dimensional discrete element model of aggregate，and provide powerful technical support for further digital test piece simulation.

Key words：highway engineering;aggregat;discrete element method;Fish code

為了对混凝土的细观结构、力学特性有更加深入的认识，基于离散元法的混凝土结构数值模拟研究逐渐成为研究热点. 构建混凝土试样离散元模型是进行细观结构分析及力学模拟的关键. 离散元建模的方法主要分为两种：一种是成型试件并通过X-ray 工业CT技术[1]及数字图像处理重构得到试件的离散元模型;另一种是基于算法和计算机直接生成离散元试件. 前者能够获取得到较为精确的试件数字模型，但由于费用较高以及试样尺寸、形状等限制而具有一定的局限性，而后者在这方面优势显著.

集料占混凝土体积的40%～60%，且集料的形态特征（棱、角、面的特征）对理解混凝土中集料的力学行为至关重要[2]. 集料形态的精确表征是计算机直接生成离散元试样进行建模的关键. 目前，集料模型构建方法主要包括理想球体化表征、不规则多面体表征、基于逆向工程重构等.

球体表征集料方法简单，计算模拟资源占用少，但该方法无法表征真实集料的几何形状特征，尤其是集料的棱角性和表面纹理特征. 在离散元建模的早期研究中，研究人员多使用球体表征集料[3-4];另外，目前在一些集料形状影响不显著的研究中也常采用球体模型[5-7]. 为弥补球体模型的不足，采用不规则多面体表征集料，一般通过开发算法并控制自定义参数创建不规则集料模型，例如多面体、椭圆体和其他不规则形状. 比较具有代表性方法包括Lu

等[8]使用球体延伸算法来生成不规则形状的集料离散元模型，不同的参数条件下可以生成不同形状的球体组合表示的不规则集料;Liu等[9]以及王江洋

等[10]使用随机平面切割球体获得多面体表征集料;Ma等[11]使用随机平面切割立方体获得不规则多面体表征集料;袁强[12]使用凸包算法构建数字集料和沥青混合料试件用于研究骨料形状对沥青混合料性能的影响;杨军等[13]将规则的二十四面体进行不同的拉伸和压缩，从而形成不同尺寸的不规则二十四面体;Yu等[14]在其沥青混合料模型中使用球体重叠粘接组合生成集料. 与球体模型相比，不规则多面体形状的模型可以简单表征集料的形态，但表征集料的棱角和面特征相对简单，准确性有所欠缺. 除上述基于算法生成虚拟集料颗粒的方法外，基于X-ray工业CT断层扫描或激光扫描等逆向工程技术进行集料的三维重构也有所进展. Liu等[15]基于Matlab及X-ray工业CT扫描技术对集料进行重构，并用于集料混合料试样的离散元模拟;张徐等[16]基于激光扫描获取集料的形态特征并进行集料模型构建，用于铁路有砟道床振动和变形的数值模拟. 目前，基于CT扫描、激光扫描等重构真实集料的数字化几何形态能够得到较精确的表征集料颗粒，但相较于基于算法完全由计算机生成虚拟集料颗粒的方法成本仍较高.

综上所述，目前基于工业CT扫描、激光扫描获取真实集料几何形态的成本较高，具有一定的局限性;由计算机算法随机生成凸多面體表征集料几何形态的方法难以反映集料颗粒针片状、棱角性以及凸凹破裂面的多样性，限制了混凝土离散元力学模拟的多因素分析. 基于上述问题及目前对于高效、低成本虚拟构建集料离散元模型的需求，拟基于三维建模技术及PFC 5.0平台FISH语言开发一种集料离散元模型构建方法. 该方法完全基于计算机平台虚拟开发，可表征集料颗粒针片状、宏观棱角、凸凹面等几何形态特征，填充方法高效，有效降低了集料颗粒离散元建模的成本. 该方法的开发将主要包含以下3个方面：①通过三维建模技术，实现集料几何形态的构建;②使用PFC 5.0读取集料几何形态特征数据，填充集料几何形态内部空间形成集料离散元模型;③针对不同形态特征的集料进行建模，初步建立一个小型数据库. 为了评价该方法的有效性及准确性，提出相关指标对集料模型的准确性进行评价，并对该方法中的相关因素对集料模型的有效性的影响进行分析.

1   集料几何形态构建

PFC 5.0离散元平台支持读取. STL格式数据构建复杂墙体及生成clump模板[17]. 本节主要通过三

维建模技术实现集料几何形态的构建，并将包含集料几何形态特征的数据以. STL格式进行输出，以用于集料离散元模型的构建.

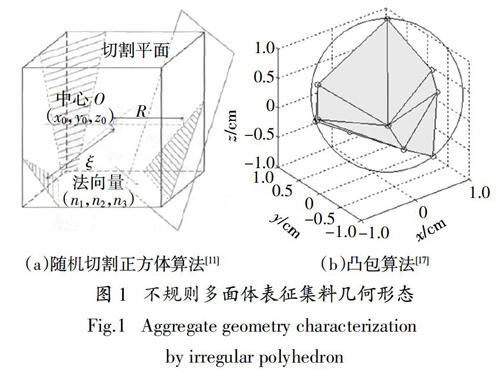
集料的几何形态对沥青混合料的体积特性、力学性能有很大的影响，在完全虚拟化生成集料颗粒的过程中，构建拟真的集料几何形态是提高沥青混合料离散元模拟准确性的关键. 目前研究常采用随机生成的不规则多面体表征集料的几何形态，难以体现真实集料颗粒的凸凹破碎面、棱角和表面纹理特征. 图1（a）所示为文献[11]通过随机切割正方体获取凸多面体表征集料几何形态，图1（b）所示为文献[17]使用凸包算法随机生成的凸多面体表征集料几何形态.

针对上述问题，基于集料颗粒不同视角图像特征，依托于三维数字化建模平台ZBrush进行集料颗粒三维可视化建模. 首先生成球体作为“基球”，然后根据颗粒多角度棱角信息将基球扩展为大致形状，最后对表面进一步调整得到虚拟颗粒的最终形态. 图2为基于三维建模获取得到的集料几何形态与真实集料颗粒的对比图.

基于三维建模获取得到的集料几何形态，相较不规则多面体更能表征集料的复杂形状，尤其在表征凸凹破碎面和棱角性方面. 为验证建模得到的集料几何形态满足使用要求，采用体积对比的方式进行形态标定. 图3（a）所示为真实集料颗粒体积测定，图3（b）所示为基于Matlab平台计算集料几何形态的体积值. 表1所示为4.75～9.5 mm的部分颗粒体积标定值，集料几何形态与真实集料颗粒的体积有一定的偏差，但偏差值都处于可控范围内，集料几何形态能够反映集料颗粒的宏观形状，可以用于集料颗粒进一步虚拟建模.

为提高集料几何形态的准确性，在建模过程中保留了尽量多的集料模型特征点，这会导致特征点的数量冗余. 过多的特征点会降低后续的颗粒填充速度，基于Matlab平台开发程序对集料特征点进行不同程度的简化. 图4所示为不同特征点数量对应的集料数字模型. 简化至5 000点左右时颗粒外观无明显变化，300～700特征点时能够保持模型的主要形态，300特征点以下时颗粒的表面纹理特征损失严重. 1 000特征点是较为平衡的数据量，该部分将会在后续的章节进行详细探讨.

根据PFC帮助文档[18]，基于Rhino平台对集料数字模型进行标定，通过集料模型最小边长、次小边长的长度可确定该颗粒所属的粒径范围. 根据上述方法可实现集料几何形态的尺寸标定，保证颗粒的尺寸满足要求.

2   集料离散元模型生成

PFC 5.0相较PFC3.0更加注重clump的使用，提供更加完善的复杂几何形态建模方法. 本节基于PFC5.0中的Bubble Pack算法填充集料几何形态内部空间以获取相应的clump模板，调用clump模板生成clump块体作为集料颗粒的三维离散元模型. 针对不同形态特征的集料颗粒，构建clump模板的数据库，用于进一步研究使用.

基于PFC5.0平台开发Fish语言程序，导入集料几何形态. 如图5（b）所示，在PFC5.0中集料几何形态仅能表征集料的表面特征，无法进行力学模拟，需要进一步对几何形态内部空间进行填充. 为缩短开发周期，使用PFC5.0平台自带的Bubble Pack填充算法[19]实现集料几何形态空间的填充. 如图5（c）所示为图10集料1填充完成的clump template，图5（d）所示为clump template剖面图.

Bubble Pack算法的基本原理是识别几何空间骨架线或骨架面，按照骨架线/骨架面方向生成大小不等的球体，逼近几何空间内部边界以实现对几何空间的填充. 如图6所示，在二维几何封闭空间S中，生成若干与二维空间边界至少有两个切点的圆，所有圆的圆心轨迹即为空间S的骨架线. 同理，三维空间中，与三维空间边界至少3个点相切的球的球心连接即可得到三维空间的骨架面.

理论上每个几何空间内可以生成无数个圆，但在实际应用中需要对生成圆的数量进行限制. Bubble Pack算法设置最小/最大球半径比值Ratio以及球体交叉角Angle来限制生成球体的数量，如图7所示比值Ratio可以控制最小球的大小，角度Angle可以控制相邻球体之间的距离.

近年来，已有诸多研究人员探索和讨论了集料几何形态空间的填充方法，比如等径小球法[11]、随机球体法[12]、球体增长法[20]等. 相较于上述算法，Bubble Pack算法可以对集料颗粒的棱角性、凸凹面信息进行更加有效的表征，填充效果有较大的提升，图8所示为不同算法之间的对比图.

等径小球是较为常用的填充方法，为量化算法的填充效果，采用填充体积与集料几何形态体积的偏差比对Bubble Pack算法及等径小球法進行评价. 如图9所示为两种算法填充效果以及填充度指标值，在填充球体数量相近的情况下，Bubble Pack算法的填充精度明显高于等径小球法.

Bubble Pack算法的实现主要通过PFC 5.0平台中clump template create命令进行实现，该命令的主要关键词包括name、geometry、surfcalculate等. 其中surfcalculate的关键词包括bubblepack、distance、ratio. 集料几何形态导入到PFC5.0后，通过clump template create命令进行填充，得到对应的clump 模板. clump模板的内在旋转状态由几何形态包含的信息计算得到，填充的单元球之间的重合不会影响clump模板的内在旋转状态. 图10（a）为调用clump模板随机生成若干相同的clump块体;图10（b）为调用clump模板随机生成若干相同的clump块体并进行随机旋转;图10（c）为调用多种clump 模板随机生成若干clump块体;图10（d）为调用多种clump模板随机生成若干clump块体并进行随机旋转.

由Bubble Pack算法填充得到的clump模板可以表征集料颗粒的形态特征，但clump模板仅保存单元球体的数据信息，无法直接应用于模型的构建及数值模拟，需要使用clump generate、clump distribute等命令调用clump模板的信息生成clump块体用于集料颗粒的力学行为. clump generate等命令的关键词size无法准确确定生成的clump块体粒径范围，为弥补上述不足，采用clump replicate命令生成clump块体，具体步骤如下：

步骤1.PFC5.0读取集料几何形态信息;

步骤2.clump template creat命令生成集料几何形态对应的clump模板，并获取该模板的体积值Vc;

步骤3.clump replicate命令调用clump模板的信息，在一定空间的随机位置生成clump块体，clump块体的体积设置为Vc;

步骤4.生成的clump块体使用clump.rotate函数随机赋予方位角，保证clump块体在空间内的随机性.

在实际工程中，集料形貌各异、分布状态多样，为简化工作量，选取形态特征具有一定代表性的集料构建离散元模型，并按照粒径进行分类组建成为clump模板小型数据库. 数据库中的clump模板可以直接被PFC 5.0平台调用，提高模型构建的效率. 不同几何形态特征的clump模板展示图如图11所示.

3   集料离散元模型评价

集料数字模型生成的效率受多种因素的影响，本节主要分析集料数字模型生成效率和精度的合理性：①分析集料几何形态特征点数量对Bubble Pack算法填充效率的影响;②提出填充度指标对填充算法的填充效果进行评价，分析算法参数对生成clump块体的填充效果的综合影响.

3.1   特征点数量对填充算法的效率影响

集料几何形态特征点的数量直接反映其包含的数据量的大小，决定了填充过程中计算量的大小. Bubble Pack填充算法采用比值R（0

如图12所示，特征点的数量大于5 000时，填充需要的计算时间急剧增加，尤其对于精度较高的R = 0.1，A = 170°参数时，计算时间增加更为明显;当特征点数量小于2 500時，不同特征点、不同参数精度的计算时间趋同. 为集料几何形态的棱角、面信息更为完整和准确并考虑填充算法的计算效率，特征点的数量控制在1 000～2 000之间较为合理.

3.2   算法填充效果评价及影响因素分析

PFC 5.0中Bubble Pack算法两个参数比值R和角度A对创建的clump template的精度有重要影响. 根据文献[18]，填充算法参数比值R是指生成的clump模板中最小单元球体直径与最大单元球体直径的比值，其值介于0和1之间，且该值越小则clump模板棱角性越突出. 参数角度A，其对应于0到180°的平滑角，角度A值越大，单元球体球心之间的距离越小，表面越平滑.

Liu等[15]对上述规律进行了初步研究，但并未对Bubble Pack算法的填充效果进行评价，本研究提出填充度指标评价Bubble Pack算法的填充效果. 集料几何形态的填充主要是使用单元球体填充其内部空间，使单元球体整体的轮廓逼近几何形态边缘，以单元球体的集合体表征集料颗粒. 如图13所示，填充算法参数变动会导致单元球体无法完全填充几何形态内部空间. 基于上述特性，提出填充度F评价Bubble Pack算法的填充效果，填充度F的计算方法如式（1）所示.

F = V_ct/V_g（1）

式中：V_ct为clump模板的整体轮廓内的体积;Vg为集料几何形态内部空间的体积.

为探究比值R与角度A对填充效果的综合影响，统计不同参数水平下clump块体的填充度及单元球体数量，如表2所示为不同因素水平下集料的填充度F. 根据统计得到的数据，绘制等高线图反映比值R及角度A对填充度F及单元球体数量N的综合影响. 受限于目前的计算能力，需要平衡clump块体精度与计算效率，即需要平衡填充度F与单元球体数量N. 如图14所示，当R越小，A越大时F值越大，N值也越大. 综合考虑比值R和角度A的耦合影响，图14（a）（b）虚线标示区域内的点对应的比值R及角度A能够较好地平衡clump块体精度与计算效率，显然处于该区域内的点2对应的clump块体填充度和单元球体数量更加满足要求.

4   结   论

本文主要介绍了一种基于三维建模技术及PFC 5.0平台Fish语言的集料三维离散元模型构建方法，并对影响该方法的多种因素进行分析. 该方法可实现完全基于计算机平台虚拟构建集料颗粒几何形态，相较于目前常采用的凸多面体表征集料颗粒几何形态的方法，能有效表征几何形态的针片状、宏观棱角、凸凹破碎面等特征，降低集料离散元建模成本，提高建模准确性，研究表明：

1）基于三维建模构建集料几何形态的方法，能够体现出集料的主要棱角及凸凹面的特征，经济易行，可满足集料离散元建模初期研究的需要;

2）集料几何形态的特征点数量较高能够保证几何形态较高的精确度，但同时制约算法的填充效率，将特征点数量控制在1 000～2 000较为合理;

3）填充算法能够高效地实现集料离散元模型填充，其参数比值R和角度A对clump块体的精度及计算量有一定的交互影响，文中推荐区域内的取值能够较好地平衡clump块体精度和计算量;

4）基于三维建模技术及PFC 5.0平台Fish语言的集料三维离散元模型构建方法能够较好平衡集料建模的精度及计算的效率，可以实现低成本、高效率生成集料离散元模型的目标.

基于目前对于经济高效、完全虚拟化构建集料离散元模型的需求开发上述方法，该方法在自动化生成、降低主观因素影响方面仍需要进一步改进，但较好地解决了目前使用凸多面体表征集料颗粒导致集料几何形态针片状、宏观棱角性及凸凹破碎面特征不准确的问题. 开发的集料模型可应用于沥青混合料、水泥混凝土的细观结构力学模拟，对于集料离散元模型构建研究具有借鉴意义.

参考文献

[1]    汪海年，张琛，方俊，等. 橡胶热再生混合料低温性能与细观特征研究[J]. 湖南大学学报（自然科学版），2014，41（11）：123—128.

WANG H N，ZHANG C，FANG J，et al. Study on low temperature performance and microstructure of rubber hot recycled mixture[J]. Journal of Hunan University（Natural Sciences），2014，41（11）：123—128.（In Chinese）

[2]    张东. 沥青混合料粗集料的形态特征研究和力学性能的离散元模拟[D]. 南京：东南大学交通学院，2013：11—14.

ZHANG D. Research on morphology of coarse aggregates and its mechanical performance by discrete element modeling[D]. Nanjing：School of Transportation，Southeast University，2013：11—14.（In Chinese）

[3]    CHANG G，MEEGODA J. Micromechanical model for temperature effects of hot-mix asphalt concrete[J]. Transportation Research Record Journal of the Transportation Research Board，1999，1687（1）：95—103.

[4]    CHANG G，MEEGODA J. Micromechanical simulation of hot mix asphalt[J]. Journal of Engineering Mechanics，1997，123（5）：495—503.

[5]    NG K，DAI Q. Investigation of fracture behavior of heterogeneous infrastructure materials with extended-finite-element method and image analysis[J]. Journal of Materials in Civil Engineering，2011，23（12）：1662—1671.

[6]    CHEN J S，HUANG B S，CHEN F，et al. Application of discrete element method to superpave gyratory compaction[J]. Road Materials & Pavement Design，2012，13（3）：480—500.

[7]    KHANAL M，TOMAS J. Application of DEM to evaluate and compare process parameters for a particle failure under different loading conditions[J]. Granular Matter，2010，12（4）：411—416.

[8]    LU M，MCDOWELL G R. The importance of modelling ballast particle shape in the discrete element method[J]. Granular Matter，2007，9（1/2）：69.

[9]    LIU Y，YOU Z. Visualization and simulation of asphalt concrete with randomly generated three-dimensional models[J]. Journal of Computing in Civil Engineering，2009，23（6）：340—347.

[10]  王江洋，錢振东，WANG Linbing. 环氧沥青混凝土裂纹发展的三维可视化离散元模拟[J].湖南大学学报（自然科学版），2014，41（6）：112—119.

WANG J Y，QIAN Z D，WANG L B. Three-dimensional visualization discrete element modeling of the crack development of epoxy asphalt concrete[J]. Journal of Hunan University（Natural Sciences），2014，41（6）：112—119.（In Chinese）

[11]  MA T，ZHANG D Y，ZHANG Y，et al. Microstructure modeling and virtual test of asphalt mixture based on three-dimensional discrete element method[J]. Journal of Central South University，2016，23（6）：1525—1534.

[12]  袁强. 骨料形状对沥青混合料性能影响的离散元研究[D]. 大连：大连理工大学交通运输学院，2015：26—29.

YUAN Q. Influence of particle shape on hma's performance：dem results[D]. Dalian：School of Transportation & Logistics，Dalian University of Technology，2015：26—29. （In Chinese）

[13]  杨军，焦丽亚，王克利，等. 基于离散元方法的沥青混合料虚拟三轴剪切试验三维模拟[J]. 东南大学学报（自然科学版），2014，44（5）：1057—1061.

YANG J，JIAO L Y，WANG K L，et al. Three dimensional simulation of virtual triaxial shear test for asphalt mixture based on discreat element method[J]. Journal of Southesat University （Natural Science Edition），2014，44（5）：1057—1061. （In Chinese）

[14]  YU H，SHEN S. Impact of aggregate packing on dynamic modulus of hot mix asphalt mixtures using three-dimensional discrete element method[J]. Construction & Building Materials，2011，26（1）：302—309.

[15]  LIU Y，ZHOU X，YOU Z，et al. Discrete element modeling of realistic particle shapes in stone-based mixtures through matlab-based imaging process[J]. Construction & Building Materials，2017，143：169—178.

[16]  张徐，赵春发，翟婉明，等. 铁路有砟道床振动和变形的离散元模拟与试验验證[J]. 岩土力学，2017，38（5）：1481—1488.

ZHANG X，ZHAO C F，ZHAI W M，et al. Discrete element simulation and its validation on vibration and deformation of railway ballast[J]. Rock and Soil Mechanics，2017，38（5）：1481—1488. （In Chinese）

[17]  邓志刚. 基于三维离散元的沥青混合料数值模拟方法研究[D].广州：华南理工大学土木与交通学院，2017：24—27.

DENG Z G. Study on numerical simulation method of asphalt mixture based on three dimensional discrete element method[D]. Guangzhou： School of Civil Engineering & Transportation，South China University of Technology，2017：24—27. （In Chinese）

[18]  Itasca consulting group inc. PFC documentation release 5.0[R]. Minneapolis：Itasca Consulting Group Inc，2014：41—47.

[19]  Itasca consulting group inc. KUBRIX？誖 Geo manual & tutorials REV05132015 version 15[R]. Minneapolis：Itasca Consulting Group Inc，2015：217—221.

[20]  YANG X，YOU Z，JIN C，et al. Aggregate representation for meso-structure of stone based materials using a sphere growth model based on realistic aggregate shapes[J]. Materials and Structures，2016，49（6）：2493—2508.